基于自適應模糊神經網絡的光儲系統優化控制

張宇寧，王海云，王維慶

(新疆大學電氣工程學院，新疆 烏魯木齊 830047)

0 引 言

隨著國家對低碳電力的大力發展，以光伏發電為代表的高比例可再生能源在電網中持續增加，但光伏出力受天氣光照和溫度影響波動較大，其并網發電的不穩定性給電網的調度帶來諸多困難[1-2]，這將嚴重制約光伏發電的大規模開發與利用，所以實現光伏出力波動小、精準跟蹤調度指令是亟待解決的研究課題。為合理應用光伏并盡量減小光伏發電的隨機性和間歇性對電網帶來的沖擊，提高系統的穩定性，需配備一定容量的儲能裝置，理想的儲能裝置應具有高能量密度、高功率密度、循環壽命長、環保節約等特性，但就目前的研究，還沒有單一的儲能方式能滿足上述特性，因此有專家提出混合儲能的概念，多種儲能方式同時工作，優勢互補，超級電容與蓄電池最為熱門，應用也最為廣泛[3- 4]。為充分發揮混合儲能的優勢，最為關鍵的是合理有效的混合儲能控制策略，一般采用低通濾波或滑動平均算法得目標并網功率和儲能系統補償功率，但此類方法未考慮電池荷電狀態的變化，易造成電池的過充過放，影響電池的壽命[5- 8]，所以在上述控制策略的基礎上，有專家學者提出加入模糊控制算法，完成對儲能設備荷電狀態的實時調節[9-10]。此類方法中的模糊控制也是采用經驗值，缺乏在線自學或自調整功能、費時費力，因此對隸屬函數和模糊規則的調整成為模糊控制過程難題[11]。神經網絡對輸入輸出數據有較強的自組織、自學習、自適應功能，Sugeno型模糊模型表達能力、推理能力較強且輸出量是清晰集合[12-15]，因此將Sugeno型模糊模型與神經網絡結合建立自適應模糊神經網絡系統可對大量歷史光儲數據進行處理，使混合儲能控制系統更加有效的跟蹤調度指令。

1 光儲系統結構

基于混合儲能的光儲系統結構如圖1所示。該系統由兩組光伏發電和一組混合儲能系統構成，經逆變控制后升壓并入電網。

1.1 混合儲能的光儲結構

基于混合儲能的光儲系統結構如圖1所示。該系統由兩組光伏發電和一組混合儲能系統構成，經逆變控制后升壓并入電網。

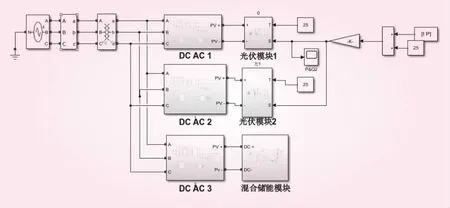
圖1 混合儲能的光儲結構示意

光儲電站調度實時指令與光伏出力偏差Per為

Per=Pd-Pg

(1)

式中，Pd為光儲電站調度實時指令；Pg為光伏出力。

調度實時指令與光伏出力偏差Per功率作為混合儲能系統的目標功率，通過自適應模糊神經網絡系統控制分頻后將高頻部分功率分配給超級電容，低頻部分功率給蓄電池，最后將混合儲能系統出力與光伏出力相加構成光儲總出力跟蹤調度指令，計算過程為

Per=Ps+Pb

(2)

Pt=Per+Pg

(3)

式中，Ps為超級電容功率；Pb為電池功率；Pt為光儲總出力。

混合儲能系統的充放電既要考慮調度的指令同時還要考慮兩者的荷電狀態情況，為了避免混合儲能運行過程中出現過沖和過放的情況，對混合儲能的荷電狀態做出相應的設置，電池的荷電狀態上下限為[0.8，0.2]；超級電容的荷電狀態上下線為[0.9，0.1]， 兩者荷電狀態的平均值通過自適應模糊神經網絡系統控制，使得混合儲能系統荷電狀態運行在合理范圍的同時跟蹤電網調度指令效果最佳。核電狀態的平均值為

socp=[(socb-0.5)+(socs-0.5)]/2

(4)

式中，socp為荷電狀態平均值 ；socb為蓄電池荷電狀態；socs為超級電容荷電狀態。

為保證光伏發電滿足并網調度要求，國家電網公司對光伏電站并網功率波動做出規定，對于15 MW及以下的光伏裝機，要求1 min內最大有功功率變化值不超過0.2 MW，要求10 min內最大有功功率變化值不應超過其對應裝機容量。

根據電網標準對光伏電站并網功率波動范圍，1 min和10 min功率波動計算式為

ΔPt.1(t)=maxPt.1(t)-minPt.1(t)ΔPt.1(t)∈[0，0.2]

(5)

ΔPt.10(t)=maxPt.10(t)-minPt.10(t)ΔPt.10(t)∈[0，15]

(6)

式中，ΔPt.1(t)、ΔPt.10(t)分別為1 min和10 min功率波動；maxPt.1(t)、maxPt.10(t)分別為1 min和10 min最大功率波動；minPt.1(t)、minPt.10(t)分別為1 min和10 min最小功率波動。

光儲出力滿足并網功率標準的區間為

Pt.(t)∈[Pt.min(t)，Pt.max(t)]=[minPt.1(t)，maxPt.1(t)]∩[minPt.10(t)，maxPt.10(t)]

(7)

2 混合儲能系統模糊控制設計

2.1 基于實測數據的模糊控制設計

對某光儲電站大量實測輸入—輸出數據經過反復試驗、篩選和整理可得出有代表性的18組數據。數據組如下

(8)

式中，n為測量的組數；p1為光儲出力跟蹤調度指令偏差；soc為混合儲能荷電狀態平均值；p2為送給混合儲能的功率指標。

根據這18組數據組歸納總結出初始模糊規則的步驟如下：

(1)根據數據組確定模糊論域。

(2)根據數據組構建模糊規則。

(3)根據“留大去小”原則決定模糊規則強度。

(4)確定模糊規則表，由以上兩輸入單輸出均為5個模糊子集覆蓋可得25條模糊規則如表1所示。

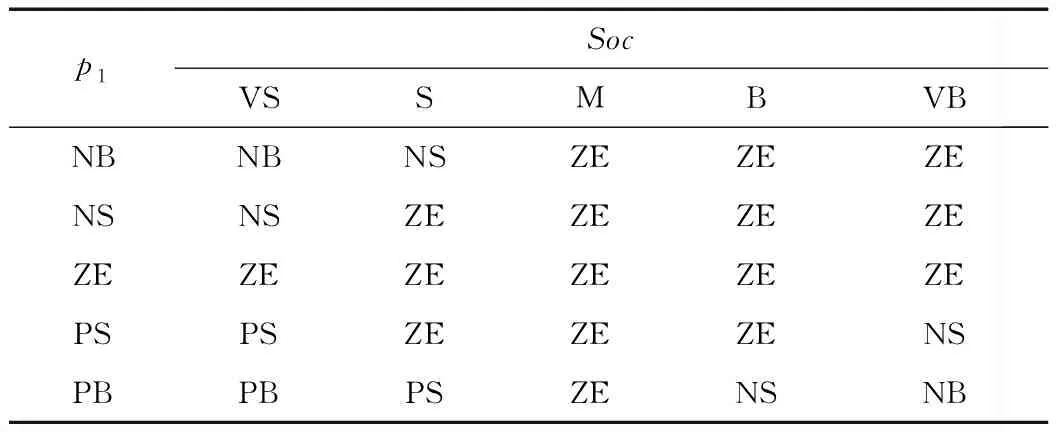
表1 混合儲能模糊控制規則

2.2 自適應模糊神經網絡的設計

2.2.1 自適應模糊神經網絡系統的建立

目前研究和應用最廣泛的一個典型的模糊神經網絡結構如圖2所示。

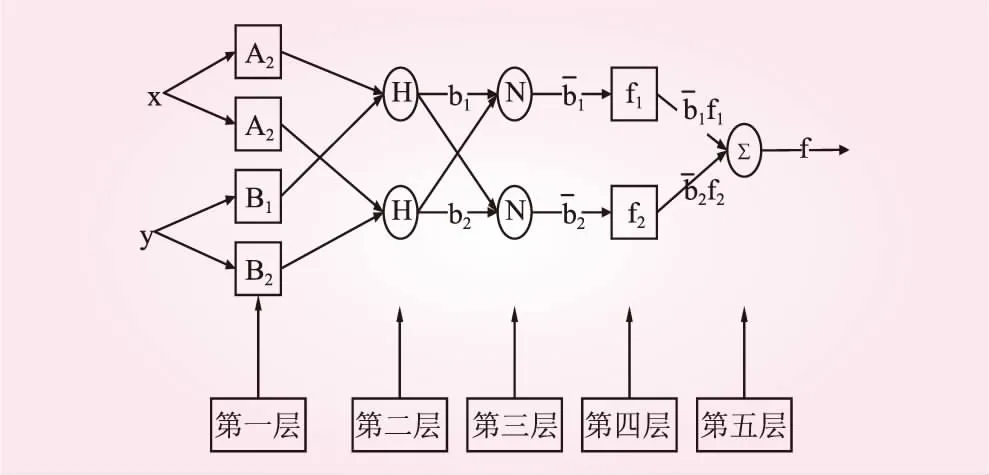
圖2 自適應模糊神經網絡結構

圖中的自適應模糊神經網絡的模糊推理是根據模糊系統的工作過程設計的5層前饋網絡結構。

第一層為輸入層，將輸入為節點數量變化的精確值隸屬度函數經過模糊化送給節點為i的參數。

(9)

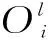
第二層為輸入層，負責將輸入信號相乘，實現輸入變量的模糊化，節點輸出為該模糊規則的可信度ai。

(10)

第三層為歸一化層，該層的第i個節點計算第i條規則的歸一化可信度，確定該層節點數為模糊規則數。

(11)

第四層為模糊規則輸出層，每個節點i為輸出變量模糊度劃分的個數，pi，qi，ri為該節點的參數集。節點i的輸出為

(12)

式中，pi、qi、ri為該節點的參數集。

第五層為清晰化層，該層將計算所有的輸入信號轉換為精確的輸出量。

(13)

2.2.2 自適應模糊神經網絡系統儲能功率分配

自適應模糊神經網絡的模糊控制器采用兩輸入、單輸出系統，輸出的功率偏差采用低通濾波器將功率分為兩部分，其中的高頻分量由超級電容負責，低頻分量由電池承擔，為便于計算，濾波器從頻域轉換到時域的傳遞函數為

(14)

式中，τ為濾波時間常數。

經t時間濾波后的超級電容器和電池的功率分別為

(15)

(16)

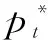
λ為與濾波時間常數τ相關的濾波系數，λ的取值范圍為[0 1]，其函數為

(17)

經驗表明濾波系數λ的控制可以實現混合儲能的能量分配，當λ較小時，超級電容功率波動較大不利于承擔功率，此時電池輸出功率較為平滑；當λ較大時，超級電容功率波動較小，負擔功率降低，此時電池輸出功率增加。

2.2.3 自適應模糊神經網絡訓練

為使自適應模糊神經網絡的隸屬度函數和輸出參數更加完善和準確，本文用大量光儲電站歷史數據對以上初始形成的模糊神經網絡系統進行訓練。

將歷史光儲電站實測數據輸入，其對應關系變為p1→x，soc→y，p2→u。將得到18行3列的矩陣，x列是光伏出力與調度偏差，y列是荷電狀態，u列是送給儲能的功率。

光儲電站數據生成自適應模糊神經網絡的結構可作為后期大量數據訓練依據，只需改變初始自適應模糊神經網絡的參數，而不會改變其結構。根據光儲電站數據自動生成的自適應模糊神經網絡的模糊子集的隸屬度函數都是高斯型，在對大量數據訓練前可以按照設計需求改變模糊子集的隸屬度函數，一般情況下采用自動生成的隸屬度函數效果較好，本模型采用自動生成的隸屬度函數。

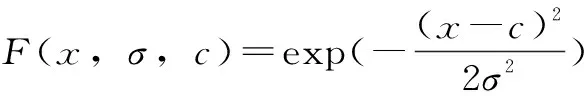
m1=1.284×10-5x+4.861×10-5y+0.000 117 4

(18)

m2=0.002 051x+0.005 968y+0.014 63

(19)

m3=0.000 979 5x+0.002 556y+0.006 314

(20)

m25=0.284 9x+0.200 7y+0.231 6

(21)

經過訓練后的自適應模糊神經網絡模糊規則的兩個輸入量，輸出量也會跟著變化，使得兩個輸入量與歷史給定的兩個參數相同，得到表2、3如下所示，例如第一個數據組輸入同為p1=0.41，soc=0.93，經過自適應模糊神經網絡訓練后的p2=0.405較初始模糊控制輸出p2=0.38更精確。

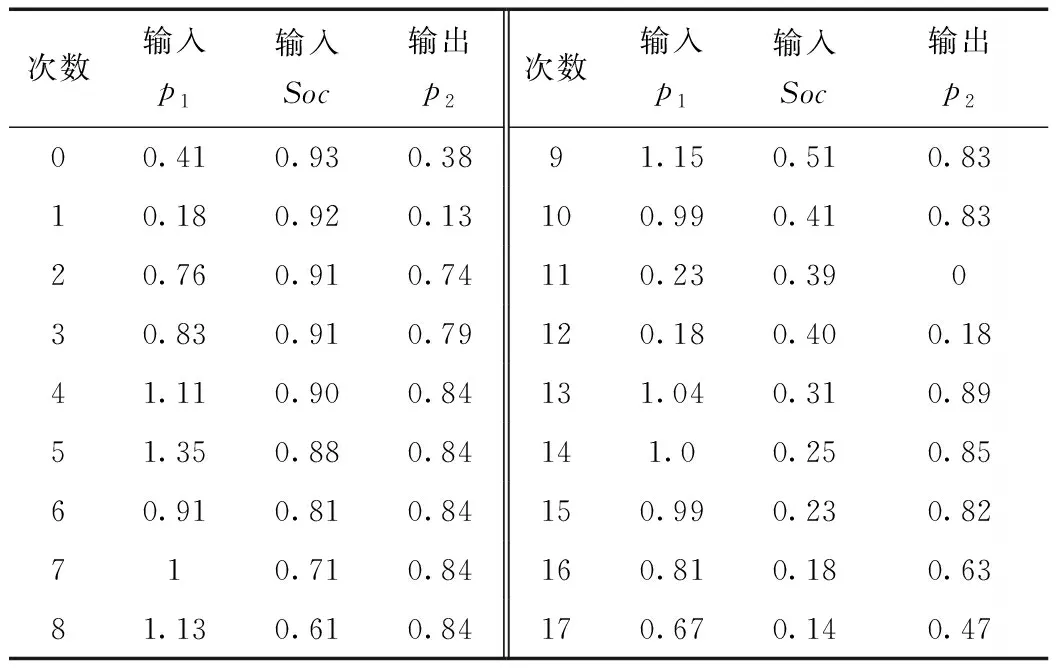
表2 初始模糊控制輸入、輸出數據

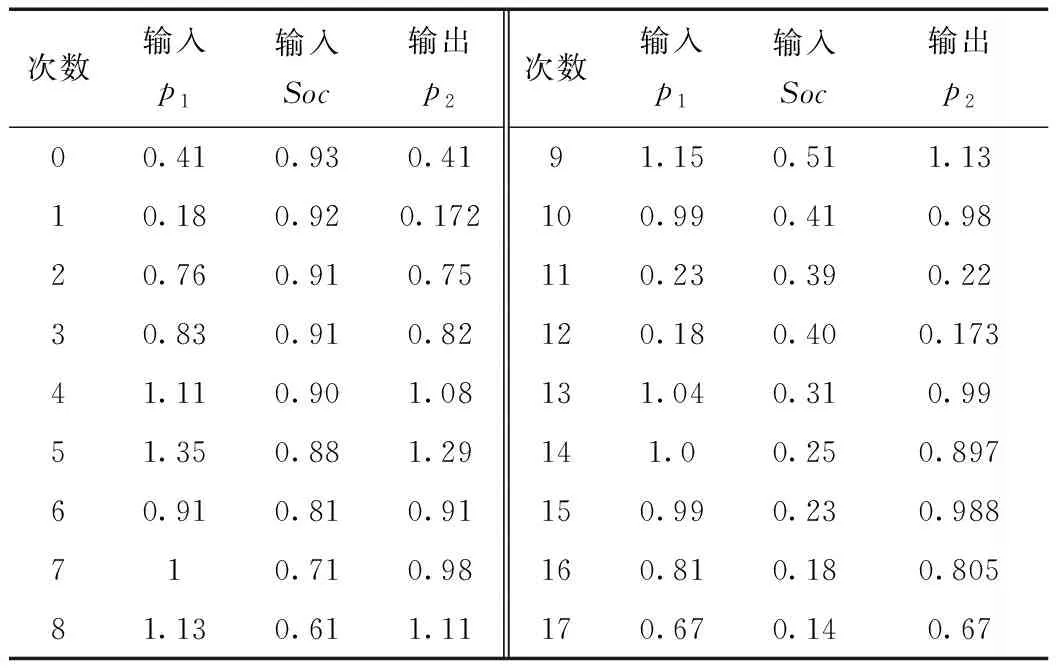
表3 訓練后的自適應模糊神經網絡輸入、輸出數據

3 仿真驗證與分析

為驗證自適應模糊神經網絡控制的有效性，仿真采用裝機容量為4 MW的光伏歷史運行數據，利用MATLAB/simulink配置1 MW的電池和超級電容組成的混合儲能系統，取光照時間良好的某天24 h歷史運行數據，由于光伏出力跟蹤調度采樣間隔為3 s，一天共計采樣頻率28 882次，將以上數據導入MATLAB仿真時間較長，本文講仿真時間為縮短為2.4 s，超級電容和電池的相關參數如表4所示。

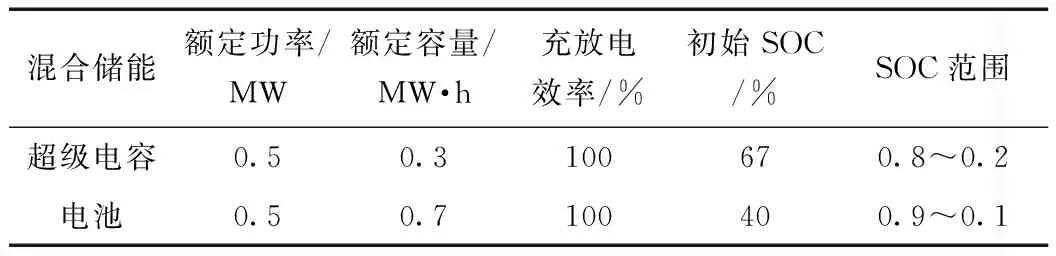
表4 超級電容和電池的相關參數

青海某光儲電站光儲出力跟蹤調度指令一天的歷史曲線如圖3所示，實際的光儲出力跟蹤電網調度指令的偏差相對較大，給電網調度工作帶來諸多困難。

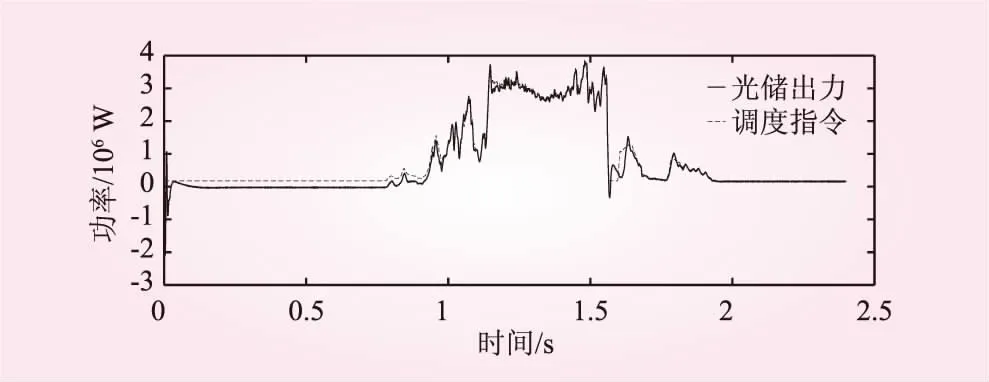
圖3 光儲出力跟蹤調度指令曲線

加入自適應模糊神經網絡優化控制前后的光儲出力跟蹤調度指令偏差對比如圖4所示，在偏差較大的1.6 s時達到1 MW，加入優化控制后的光儲出力跟蹤調度指令偏差放大效果如圖5所示，從放大效果圖可以看出初始模糊控制和自適應模糊控制在最大偏差時降低到0.85 MW，自適應模糊控制后的功率偏差下降的更快，表明跟蹤調度指令速度快、幅值偏差小。

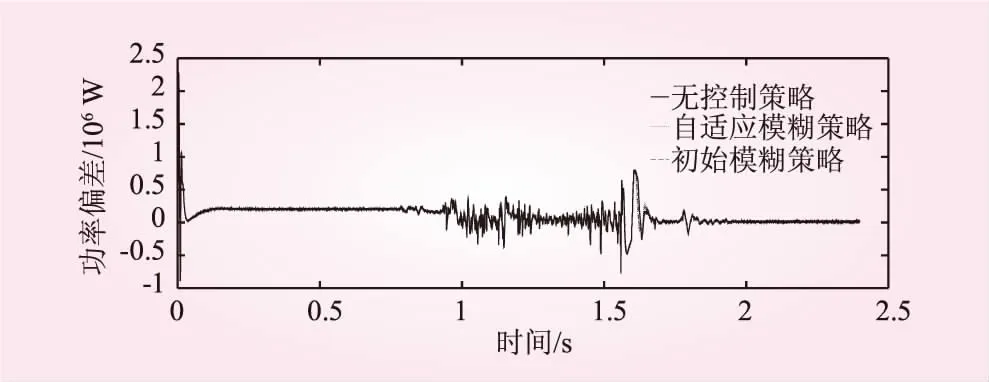
圖4 加入自適應模糊神經網絡優化控制后的光儲出力跟蹤調度指令曲線

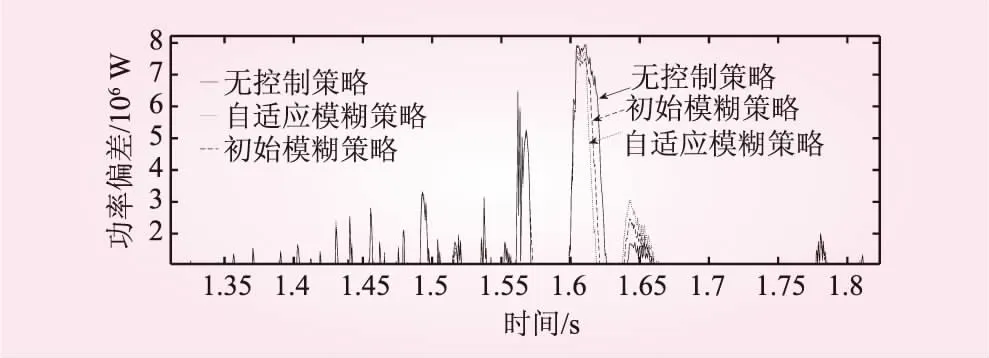
圖5 加入自適應模糊神經網絡優化控制后的光儲出力跟蹤調度指令曲線局部放大圖

加入自適應模糊神經網絡優化控制前后的電池荷電狀態波動對比如圖6所示、超級電容荷電狀態波動對比如圖7所示，從圖6中可以看出，3種控制策略的電池荷電狀態均在10%～90%之間，加入初始模糊控制和自適應模糊控制策略的在1.6 s后荷電狀態快速恢復40%，自適應模糊控制策略恢復速度和幅值較快。從圖7中可以看出三種控制策略的超級電容荷電狀態均在58%～78%之間，自適應模糊控制策略的超級電容荷電狀態基本維持在初始的67%，整體荷電狀態波動最小，有效保護了超級電容的充放電深度。

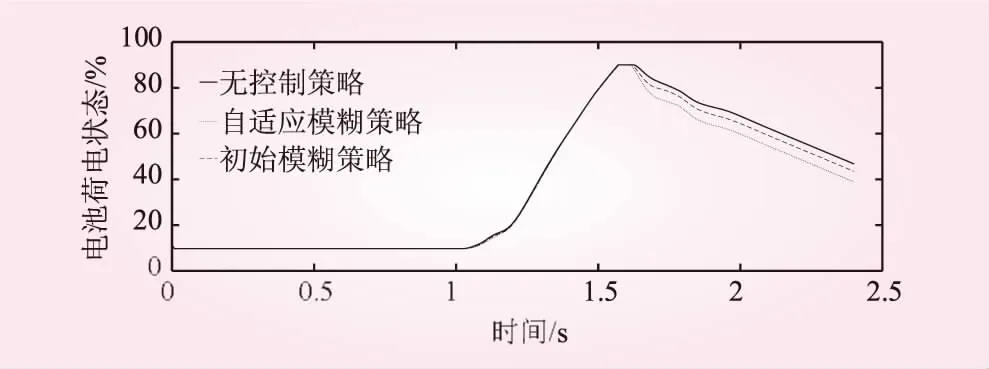
圖6 加入自適應模糊神經網絡優化控制前后的電池荷電狀態曲線

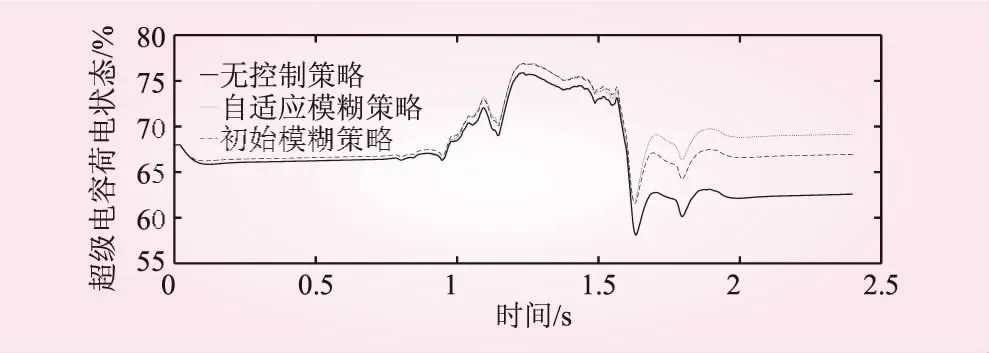
圖7 加入自適應模糊神經網絡優化控制前后的超級電容荷電狀態曲線

加入自適應模糊神經網絡優化控制前后的超級電容電壓波動對比如圖8所示，由圖可知超級電容充放電期間，加入優化控制后的超級電容器電壓波動較之前小很多，尤其是在電壓最低點，其放大效果如圖9所示，從圖中可以看出加入自適應模糊神經網絡優化控制提升了最低點電壓50 V，使得超級電容電壓波動相對減小，有利于維護系統直流側的電壓穩定。

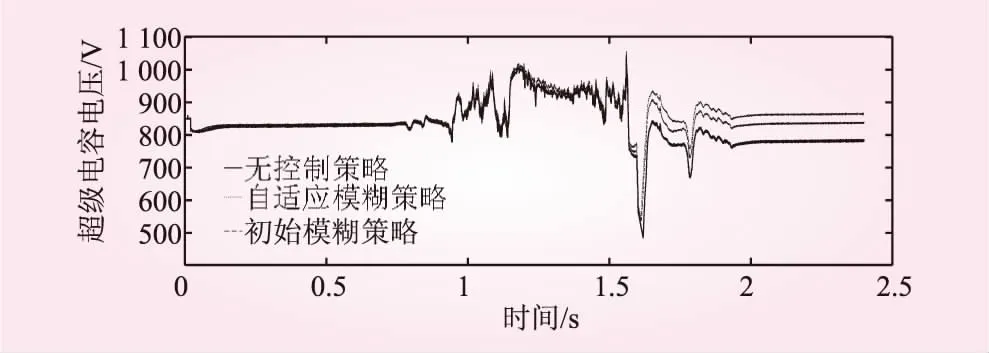
圖8 加入自適應模糊神經網絡優化控制前后的超級電容電壓波動對比

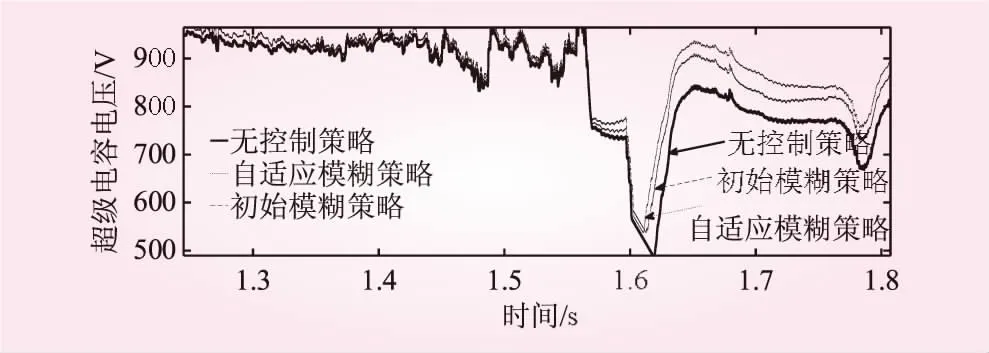
圖9 加入自適應模糊神經網絡優化控制前后的超級電容電壓波動對比

加入自適應模糊神經網絡優化控制前后的超級電容電流波動對比如圖10所示，加入初始模糊控制和自適應模糊控制策略的在1.6 s之后，放完電后的電流能快速恢復，其放大效果如圖11所示，從圖中可以看出加入自適應模糊控制策略的電流恢復較其他控制策略快0.1～0.3 s之間。

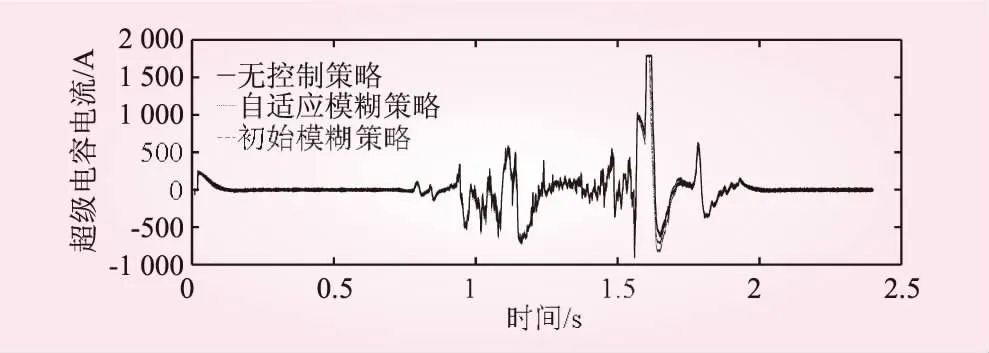
圖10 加入自適應模糊神經網絡優化控制前后的超級電容電流波動對比

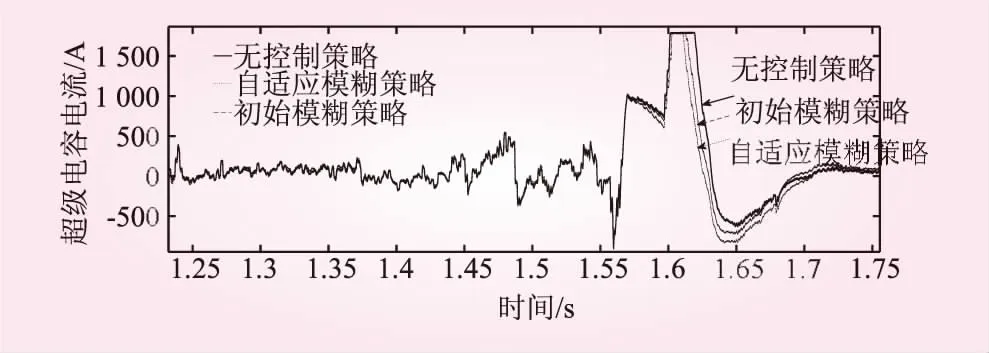
圖11 加入自適應模糊神經網絡優化控制前后的超級電容電流波動對比

加入自適應模糊神經網絡控制前后的儲能誤差指標對比如表5所示，從表中的指標可以看出，加入優化控制后的儲能在平均絕對百分比誤差、最大百分比誤差、均方根誤差的3個指標得到了明顯的改進，驗證了自適應模糊神經網絡控制的混合儲能光儲電站在跟蹤調度指令精度方面得到提升，有效提高了電網對光儲電站的調度的可靠性。

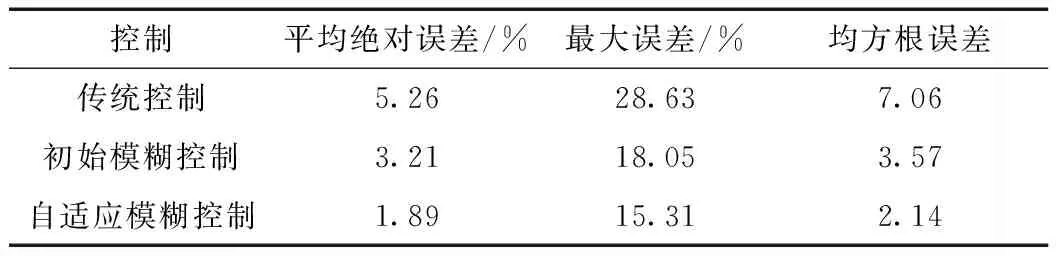
表5 加入自適應模糊神經網絡控制前后的儲能誤差指標對比

4 結 語

通過混合儲能性能上的互補作用實現光儲出力跟蹤調度指令，提出一種新型自適應模糊神經網絡的光儲系統優化控制策略，在對某光儲電站大量實測輸入—輸出數據中，經過反復試驗、篩選和整理得出有代表性的數據生成初始模糊控制，對其進行自適應模糊神經網絡控制的訓練，經過訓練后的優化控制輸出功率采用低通濾波方法分解為高、低頻分量分別給超級電容和電池，可有效提高光儲出力跟蹤調度指令精度混合儲能荷電狀態運行在合理范圍內的同時，有效減小了超級電容器充放電時的電壓、電流波動，在MATLAB/SIMULINK上對光儲電站的歷史實測數據驗證了該控制策略的有效性，對實際光儲混合儲能電站出力跟蹤調度指令具有實際指導意義。