利用軟計算技術改善圓錐滾子軸承的工作性能

盧彥群，侯建偉

（河北工程大學，河北 邯鄲 057000）

1 前言

雙列圓錐滾子軸承（TRBs）用于在靜態和動態條件下支撐預緊力（P）、軸向載荷（Fa）、徑向載荷（Fr）和扭矩（T）等 4 種載荷及其組合。該類軸承由 2 個內圈、1 個外圈和 2 組圓錐滾子組成，2 個內圈之間由一個等寬的間隙（δ）隔開，圓錐滾子在內、外圈之間形成兩列。δ 的作用是便于調整軸承的整體游隙和預緊力，并便于承受 P、Fa、Fr和 T 的作用。組合式載荷會在軸承滾道上產生接觸應力（S）和局部變形（α），也會引起滾道自身的旋轉和 δ 的變化，這很難進行實驗預測和驗證，此外，如果軸承上承受的載荷與制造商的建議值不同，則軸承可能出現故障。譬如，如果 P 值較小，Fr和 T 值很高，則可能在滾道上產生超過 1 000MPa 的 S 值和顯著的局部變形（αmax）。這可能會導致缺陷產生，如點蝕和疲勞剝落[1]。除了這些不希望的摩擦學問題外，P 的降低可能導致外滾道的某些接觸區域產生更大的應力，進而導致滾子脫離外滾道[2]。因此，通常通過分析技術或數值方法（如有限元法——FEM）來確定此類機械裝置的最佳載荷組合。雖然使用有限元法有許多明顯的優勢，但它的確也有一些缺點：比如在利用有限元模型處理機械接觸、大位移和材料非線性問題時，會產生高昂的計算費用，且在處理機械接觸問題時的一個最大缺陷是網格尺寸及模型收斂問題，也就是說，如果圓錐滾子和滾道之間的接觸面較小，而兩個接觸體之間的單元格尺寸較大，則接觸應力的計算將不太準確[3]。一些研究人員[4]采用這種方法，分析了在若干種 P 和 Fr作用情況下的接觸體網格尺寸對圓錐滾子和滾道之間接觸應力的影響。

眾所周知，單獨使用有限元（即沒有軟計算或數據挖掘——DM技術）來優化運轉工況或預測軸承故障的設計方法，涉及到不可接受的計算成本問題。因而，為了預測安裝在雙列 TRB 上的輪轂的接觸應力分布，洛斯塔多等人使用了基于 DM 技術的各種類型的回歸模型。其應力分布由 P、Fr和摩擦系數決定，所得回歸模型可作為該類機械裝置設計階段的可行方案。此外，為了優化這些機械裝置的運行狀況，洛斯塔多等人[5]還采用了有限元和 DM 相結合的方法，以確定雙排 TRB 的最大承載能力。在這種情況下，研究的重點是找到輸入載荷（P、Fa、Fr和 T）的組合方式：當兩排滾子的接觸應力比都接近 25% 時，Fr最大，即此時具有最大承載能力。其他一些研究者使用基于機器學習法的分類技術來事先預測軸承的失效與故障，這些預測滾子大多數僅僅依賴于實驗數據。例如，為了預測滾動軸承的失效，蘇古曼等人采用了決策樹以及基于內核的鄰域得分和多類支持向量機（SVM）等手段，其中涵蓋了狀態良好的軸承、內圈故障的軸承、有外圈故障的軸承和有內外圈同時存在故障的軸承。格里亞斯和安東尼亞迪斯[6]使用 SVM 方法對滾動軸承故障進行自動診斷，這是一種有效的方法，在滾動軸承故障診斷中具有潛在的應用價值。最近，康卡等人采用人工神經網絡（ANN）和 SVW 檢測和診斷滾珠軸承的機械故障，通過對各種缺陷的振動響應分析，對神經網絡和支持向量機進行訓練和測試，結果表明，上述算法可用于軸承故障的自動診斷。蔣川等人提出了一種新穎的、基于經驗的小波變換和模糊相關分類的滾動軸承故障診斷新方法，實驗表明，該方法能有效地診斷滾動軸承的三種不同工作狀態，且檢測率高于 SVW 和反向傳播神經網絡（BPANN）。

新近出版的文獻采用基于 FEM 和 DM 相結合的分類技術，來探究 TRB 的最佳運行條件。用于對定義承載條件的明確響應進行分類的 DM 技術可分為有監督數據集和無監督數據集[7]。在有監督數據集中，每個數據實例的類標簽是已知的，新實例由構建模型進行預測；然而，在無監督數據集中，沒有實例標簽，且可以用一組特定的相似度量對實例進行分組。有監督數據集和無監督數據集技術都有應用，但鑒于無監督技術的結果不能令人滿意，故在該項工作中對有監督技術給與了更多的關注。無監督分類算法是基于有限正態混合模型的一種聚類算法，而有監督分類算法數量較多，本文將其分為以下幾種：線性分類法、非線性分類法、分類樹和基于規則的分類法。

本文的主要目標是建立精確的模型，以更高的精度自動區分雙列 TRB 的預設運行狀態——從幾個預先配置的 P、Fa、Fr和 T 負載組合來定義該狀態（例如：壞、差、好和優）。分類模型可以提供運行狀況的相關信息，包括某些不良狀況的附加信息，比如過高的接觸應力、過大的局部變形、點蝕和疲勞剝落等。為了實現這一目標，將機器學習法應用于從雙排 TRB 的有限元模型中所得的數據集，這些若干負載下的數據集可以定義實驗設計（DoE）后的運行狀況。而后，創建了幾個模型并對其特征進行約減、數學變換和參數整定，接下來，根據幾個魯棒性標準對所選模型進行測試，以確定其泛化程度[8]。

2 材料與方法

2.1 雙列圓錐滾子軸承的負載組合與滾子條件

圖1a 顯示了施加在每個 TRB 部件上載荷狀況（P、Fa、Fr和 T）：內滾道上施加 P 荷載，外滾道上施加 Fa、Fr和 T 荷載。內圈被 δ 分隔成兩邊對等的滾道，以便于軸承的拆卸和 P 的施加。由此可以理解，影響 TRB 的載荷是怎樣組合而成的，軸承是否可能會出現故障。例如，如果 TRB 上的組合載荷值等于制造商的建議值，則 δtop應等于 δbottom（見圖 1a），此時，外滾道的頂部和底部區域的接觸應力值不等于零（見圖1b），在這種情況下，所有滾子始終與內外滾道保持機械接觸，而且局部變形量與接觸應力也較小，這樣可以避免出現疲勞剝落和點蝕。與此相比，如果軸承承受不恰當的載荷（例如：過高的 Fr和 T 值，再加上較低的 P 值），那么 δtop與 δbottom則會不同，其結果會導致的 TRB 故障運行（見圖1c）。如圖 1d 所示，只有一小部分外滾道（上部區域）承受非常高的應力，而外滾道底部區域的接觸應力值則為零。這將導致出現點蝕和疲勞剝落，進而導致 TRB 故障。為了量化具有兩列滾道軸承滾子的“懸起”效應，對 TRB 的每列滾子的接觸比 S 做如下定義：

圖 1 所研究軸承的主要組成與負載

式中，Stop為各列滾子的頂部接觸應力，Sbottom為各列滾子的底部接觸應力。如果兩列滾子的接觸比（S1和 S2）大于 20%，則可防止 TRB 滾子懸起。

此外，為了量化軸承滾道的旋轉效應，從而判斷軸承故障，將間隙差（Δδ）做如下定義：

式中，δtop為 TRB 頂部內圈間隙；δbottom為 TRB 底部內圈間隙。TRB 正確運行的最佳條件是其Δδ 已盡可能減小。

但是，為了盡量減少外滾道的正常局部變形，以避免出現點蝕或疲勞剝落，在埃詩曼等人研究成果的基礎上，提出下式：

式中，αmax為最大局部變形量；dr為圓錐滾子的平均直徑（此處，其值等于 11.3 mm）。所以，作為一般規則，本案例中的 αmax的值在任何點都不應超過外滾道 0.001 13mm。

一旦確定了 TRB 能夠正常工作的條件，就要考慮各工況下 δ、α、S1和 S2的取值范圍。本文將工況分為四類（壞、差、好和優），每類工況示蹤的實例數如下：“壞”工況，試驗 15 例，檢測 4 例；“差”工況，試驗 16 例，檢測 14 例；“好”工況，試驗 27 例，檢測 6 例；“優”工況，試驗 25 例，檢測 6 例。表 1 根據檢測結果概括了各工況下的參數范圍。

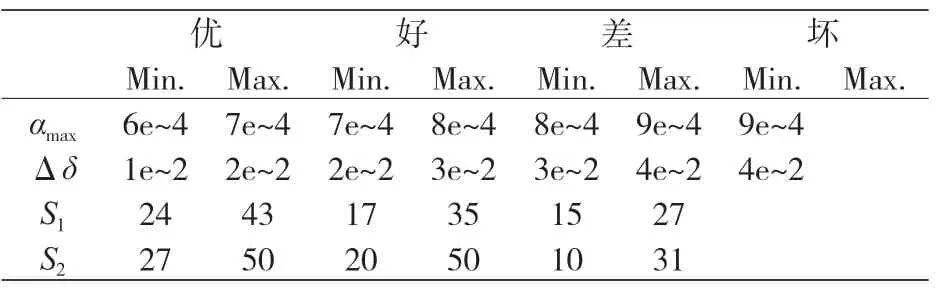
表1 各類工況下的參數取值范圍

2.2 雙排 TRB 的建模與實驗驗證

在本案例中，為研究不同載荷組合，建立了的軸承三維有限元模型（其中包括圓錐滾子、內外滾道及用來安裝 TRB 的輪軸），并利用一個雙列 TRB 的一半模型進行了模擬。為了降低仿真計算成本，本案例僅考慮對稱幾何條件和對稱加載狀況，且將 8 節點和 6 節點的三維有限元結合起來，并使用線性函數進行完全積分，從而構建 TRB 有限元模型。該研究所涉及的 TRB的幾何尺寸為：孔徑 78mm，外徑 130mm，寬度90mm，每列 25 個圓錐滾子。根據經驗并結合實際情況，假設輪軸和內圈之間的摩擦系數為0.2，滾子與內圈之間以及滾子與外圈之間的摩擦系數為 0.001。完整的 TRB 有限元模型由 734 84個單元、84 009 個節點和 3 289 個自由度組成。與傳統的“節點-段”接觸檢測算法相比，“部分分隔”接觸檢測算法能夠減少計算接觸應力的誤差，同時可以減少接觸應力的網格密度[9]，為了改善 TRB 不同部分之間的機械接觸檢測質量，本研究選擇了后者。整個有限元模型的雅可比因子始終大于 0.6，因此，沒有生成零體積的元素，此外，任何元素的縱橫比（定義為元素最長邊緣與其最短邊緣之間的比率）從未超過10:1。

在材料屬性上，賦予圓錐滾子與滾道以線彈性和各向異性鋼，且滾子的楊氏模量（E）為 208GPa，泊松比（ν）為 0.29。輪轂是以E = 200GPa 和 ν = 0.29 的假設而建模。TRB 的不同組成部分如圖 2a 所示，調整后的有限元模型最終網格尺寸如圖 2b 所示。

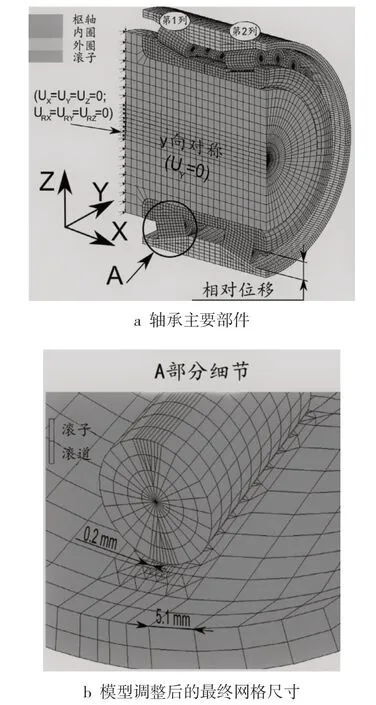
圖 2 三維有限元模型

該案例對所提出的有限元模型進行了調整和實驗驗證，使所得結果盡可能真實。這一過程通過對接觸運動副（滾子和滾道）的網格尺寸以及滾道之間的相對位移的調整來實現，其中施加的力 P 分別為 300、400、500 和 600 N，力 Fr為 2 000N。

2.2.1 滾子與滾道網格尺寸的匹配

眾所周知，機械接觸問題中的非線性是有限元法求解實際接觸應力的主要難點之一。就這類非線性問題而言，有些有限元模型只具有有限的接觸面，而網格尺寸很大，這很可能產生不切實際的接觸應力。這一問題往往通過使接觸副之間的網格更小化來解決，即增加接觸節點的數量，或增加有限元模型函數的多項式次數[10]。為此，德米漢和坎伯對圓柱滾子軸承的有限元模型進行了調整。該案例研究了單元格大小對滾道與滾子接觸應力的影響以及內外滾道的相對位移等情況，同時還對滾子和滾道之間不同網格尺寸的接觸應力與理論數據進行了比較，其間，當有限元模型所得結果與理論和實驗所得結果之間的差異不顯著時，模型調整完成。類似于德米漢的工作方式，本案例逐漸遞減網格尺寸，相繼構建出含局部精細網格接觸區域的有限元模型。這種通過使用漸小化網格尺寸來創建連續網格的方法需經過不斷改進，直到這些有限元模型外滾道上的接觸應力與理論模型上的接觸應力幾乎沒有差異為止。本案例以赫茲[11]圓柱體理論模型為基礎，對所提出的有限元模型的不同網格尺寸進行了比較，并使用平均絕對百分比誤差（MAPE）來確定有限元模型的網格大小何時有效。MAPE 的定義如下：

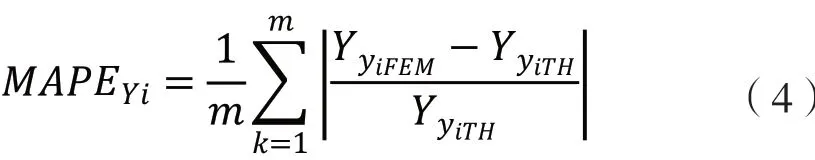
式中，YyiFEM為每個有限元模型在不同擬用網格尺寸時的接觸應力；

YyiFEM為理論模型中的接觸應力；m 為各尺寸網格下的節點總數；

k 為局部接觸區各節點的接觸應力之一；

yi 是調整參數，在本案例中對應于接觸面積元素的網格大小。當接觸元素（包括滾子和滾道）接觸區尺寸分別為 5.1、1.0 和 0.2 mm時，網格尺寸調整所獲得的 MAPE 如表 2 所示，它顯示了預加載 P 分別等于 300、400、500 和 600 N 和

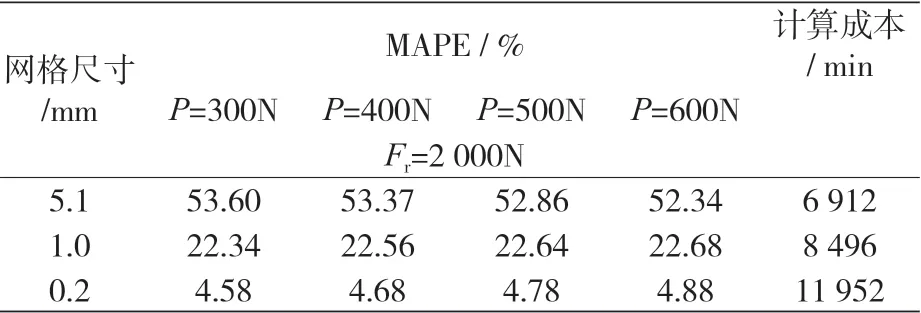
表2 調整網格密度時，有限元模型的MAPE及其計算成本

Fr等于 2 000 N 時的 MAPE，此外還對每個網格所需的平均計算時間進行了探討。

根據經驗，當 MAPE 小于 6% 時，才被認為是合理的，當然還要考慮計算成本，因為對任何使用 FEM 解決的問題，其 MAPE 和計算成本都要達到預期的目標，以此為準則，本案例中滿足此要求的要素是那些網格尺寸為 0.2 mm 的單元格（對所有的 P 進行預加載和模擬，其 MAPE 和計算成本均低于閾值）。

2.2.2 基于滾道相對位移的 TRB 的調整

在有限元模型的驗證中，但凡對網格尺寸做出調整，都要考慮內外滾道的相對位移的變化，因為內外滾道的相對位移主要用于檢驗有限元模型的網格尺寸、摩擦系數和彈性特征（E 和 v）的是否恰當。實驗中，用圖 3a 中所示的、帶有 2 只紅色鉛筆的比較儀來測量該相對位移，在有限元模型中，該位移在屬于模型本身對稱平面的兩個節點之間進行測量，如圖 2a 所示。在網格尺寸調整過程中，載荷 P 值分別為 300、400、500 和 600 N，Fr值為 2 000 N。Fr通過加載單元（型號為 HBM U3，加載能力為 5kN）施加于 TRB，P 由一個螺絲通過一個鋼質套管施加在軸承內圈上，用一個安裝在套管上的應變儀來測量 P 值，在擰動螺絲時，套管壓向內圈。圖 3b 顯示了不同 P 值和 Fr值下，從試驗臺獲得的相對位移與從有限元模型獲得的相對位移之間的差異：虛線表示實驗產生的相對位移，實線表示有限元模型產生的相對位移。這些成對兒的曲線表明，所獲得的這兩種相對位移之間的差異較小，此外，圖 3b 也表明，無論是有限元模型還是實驗數據，當施加最低的 P 時，相對位移較大，當施加最高的P時，相對位移最小，同時圖 3b 還表明，隨著預緊力的增加，滾道與滾子接觸剛度增加，TRB 變形減小。圖 3c 表達了通過實驗和有限元模型得出的不同相對位移值的詳情，這種剛度變化與考茲拉絲和卡尼亞[12]之前報道的荷載-撓度關系非常吻合，這表明 TRB 中的預載值越高，其剛度越大。從圖 3b 還可以推斷出：如果網格尺寸有效，那么與實驗數據和有限元模型的預設參數（Ebearing= 200 Gpa，Ehub= 208 GPa，ν = 0.29，摩擦系數 = 0.001 和 0.2）相一致。雖然優化過程中使用的荷載比網格調整過程中使用的荷載高（見表 4），但在 2.2.1的預設參數和網格尺寸描述中，已經為優化過程中的所有有限元模擬做了設置。這主要是因為在優化過程中 TRB 所承受的載荷始終在廠家規定的范圍內，所以，TRB 的所有部件都不會發生永久性變形。

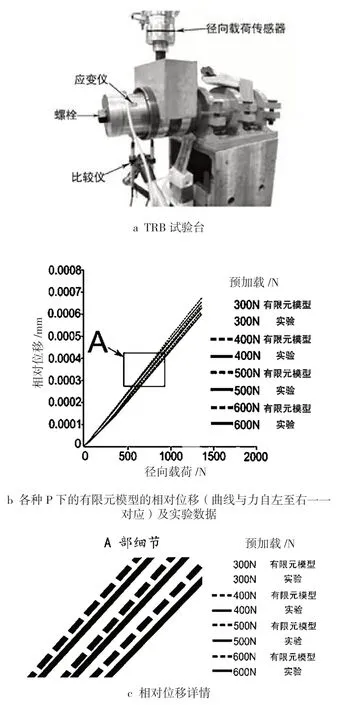
圖 3 內外圈相對位移監測

2.3 實驗設計

因為需要考慮的變量和因子的數量及每個變量的級差非常多，所以，所取樣本數無法覆蓋整個可能性空間，因此，實驗設計在這項工作中的應用，大大減少了取樣組合，在模型所需的樣本數量和有限元模擬實際需求之間，提供了一個很好的折衷。本案例實施了 3 個層級的 3k 全因子DoE，其層級與因子數值見表 3。

在建立了如表 3 所示的因子和層級后，生成了設計矩陣和荷載組合。該案例必需要進行 81次實驗或有限元模擬，以盡量涵蓋所有可能性，并隨之優化預設負載，以改善雙排 TRB 的工作條件。表 4 給出了所實施實驗或有限元模擬的次數，以及要模擬的負載值。

表3 基于各因子和3K全因子法的DOE參數、范圍、等級選擇

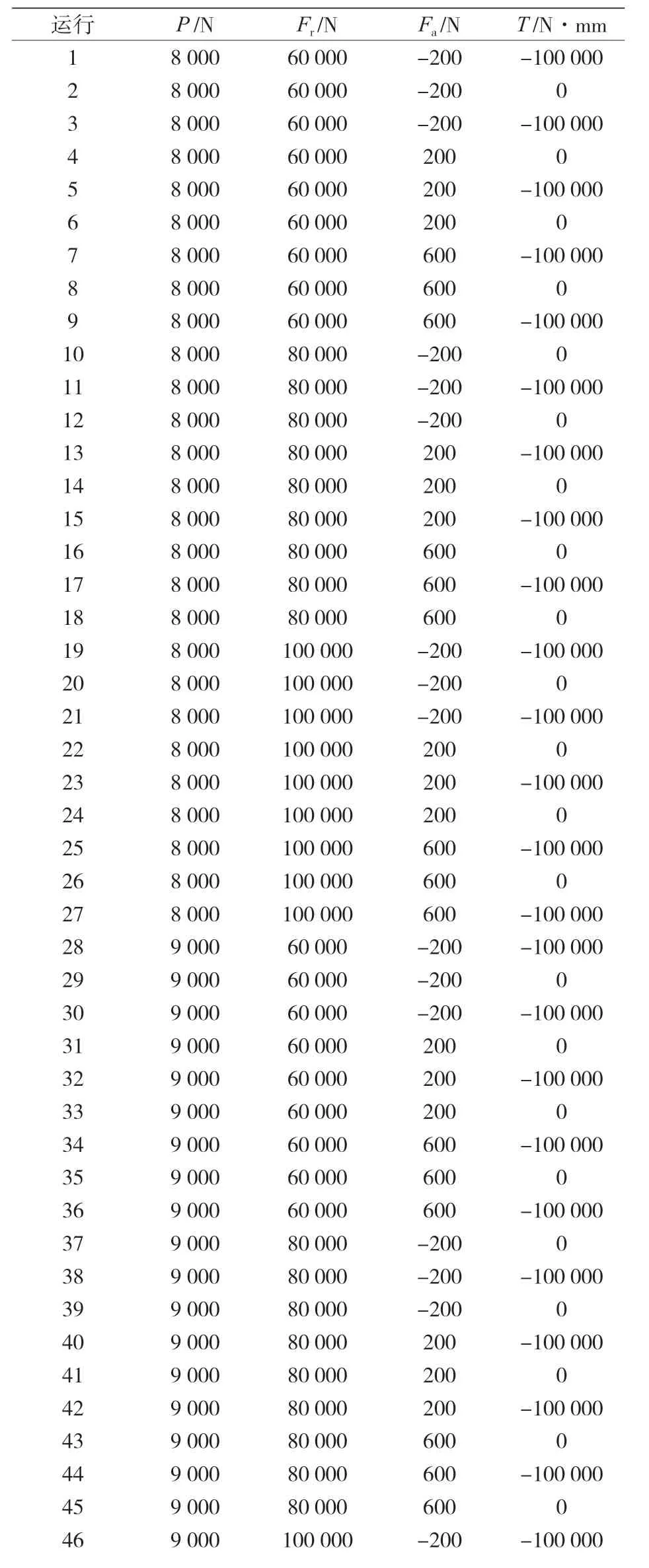
表4 設計矩陣及擬模擬的載荷組合

?

2.4 數據的多變量與聚類分析

為了平衡變量的權重并改善統計分析結果，首先，在使用分類方法之前，對所有數據集中的變量，都在 0 和 1 之間進行了規范化處理，然后，對差異性和相關性進行了探索性分析，對方差進行了統計分析。方差統計涵蓋參數性分析和非參數性分析，包括方差分析、巴特利特檢、布朗-福賽斯分析以及弗萊格-凱琳檢測[13]等。這些分析旨在確定每個特征的意義，確定這四類方法之間是否存在顯著差異，是否包含任何冗余特性，此外，主成分分析（PCA）生成了一個具有新特征的新的數據集，并在隨后對其進行了研究。差異和相關性分析是一種流行的方法，成功地運用于該課題[14]，它產生變量初始空間的正交變化，以創建一組稱為主成分（PCs）的變量。正交投影捕捉數據中的大部分方差，并將一組相關成分轉換成一組非線性相關的成分。此外，為了最終應用所提出的分類方法，對所提出的DoE中的數據進行了聚類分析，以確定輸入變量是否能夠便捷地定義分類問題。

2.5 監督分類法

該課題采用了幾種監督分類技術，按照所研究的四個類別對雙排 TRB 的呈現條件進行分類。

表5 采用的分類技術

為完成這一過程，將包含選定特征的數據集用作輸入，而這些特征定義了預設條件（P、Fa、Fr和 T）。為了簡化模型，建立了魯棒性更好的分類模型，對其進行了特征約簡和參數調整，而后，對這一階段的模型進行了測試，以確定它們的實際推廣能力，此外還對模型的性能測試結果進行了比較，以確定和選擇最準確的模型，最后，對結果進行驗證，以確保模型能夠在不經過量訓練的情況下，盡量解決更多問題。

整個分類過程按照以下方法進行：把數據集分成 2 組——第 1 組叫做訓練數據集，由計劃 DoE 的 81 個樣本組成；第 2 組叫做實驗數據集，由在 DoE 中所建議范圍內的一些隨機實例所形成（32 個樣本）。選擇訓練數據集并使用重復 10 次的交叉驗證來構建和培訓模型。由于某些方法（例如，神經網絡或支持向量機）在學習過程中使用隨機初始值，因此該培訓有必要多次重復（本案例重復了 50 次），以提高結果的準確性。在培訓過程中，設法調整每種算法的最重要的參數，以獲得更好的結果，對于每種算法，選擇最精確的模型進行測試，而且在此期間使用了尚未用于培訓的數據集。這種測試可以選擇最精確的模型，因為它們的精確性是通過以前未使用的實例來確定的。對于每種分類技術，在選擇了最精確的模型后，對該選擇過程進行了驗證，結果表明，所選模型能夠成功地解決各個方面的問題，最后，根據這些最精確的模型，對最優預設值進行了最佳分類，確保了 TRB 的正確的工作條件。

2.6 魯棒性準則

模型的魯棒性是模型選擇中一個實用的參數，而其作為一個目標函數，通常情況下需要通過 95% 置信水平下的整體分類來驗證其精度。當總體分類準確度相似（比如：靈敏性、非加權卡巴統計、特異性、檢出率、發病率、陽性預測值、陰性檢出率、預測值和平衡精準度等）時，也考慮其他標準（見表 6）。

表6 優化分類模型準確性且可以選擇最佳分類模型指標

在 v3.4.1 統計軟件環境下，用 R 語言對提議的方法進行編程，并開發分類模型[15]。

3 結果與討論

3.1 FE 模型結果

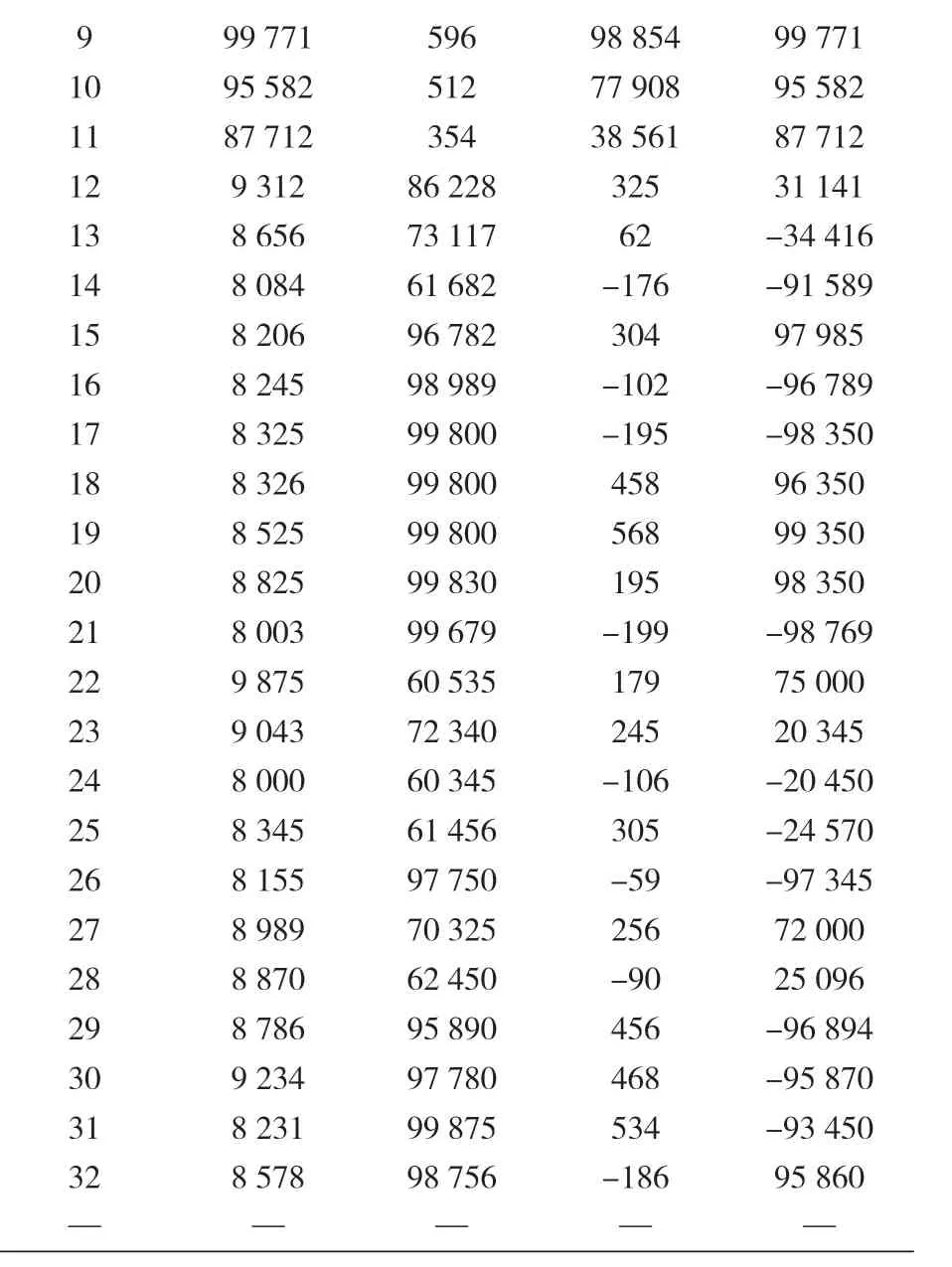
一旦 FE 模型通過驗證，自動程序則會根據表 4 中所建議的 DoE 進行 81 次有限元模擬，其結果如表 7 所示（S1、S2、αmax和Δδ）。

表7 基于表4定義的DoE的81次有限元模擬結果

?

圖 4 表達了根據施加荷載（見表 1）情況和從有限元模擬（見表 7）結果中獲得的數據集分布，其中圖 4a 顯示了αmax、S1和 S2的三維圖形數據集分布，圖 4 b 顯示了Δδ，S1和 S2的三維圖形數據集分布。在這兩個圖中，都可以看到與優、好、差和壞條件相關的圖案結構。

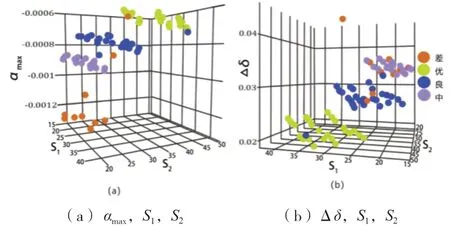
圖 4 載荷與模擬數據集分布

此外，32 個新的有限元模型被用于新的荷載組合測試分類程序（見表 8），同樣，用一個自動程序來運行 32 個新的有限元模擬，其結果見表 9。

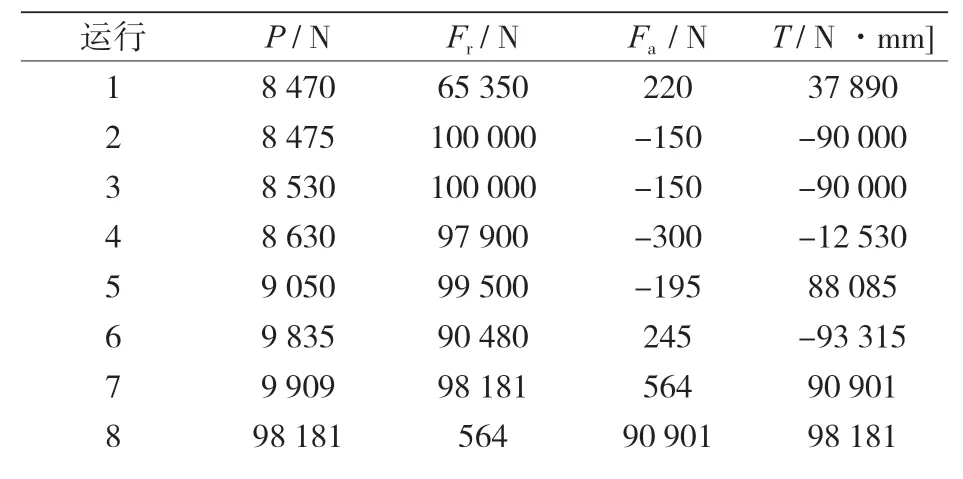
表8 新荷載組合模擬

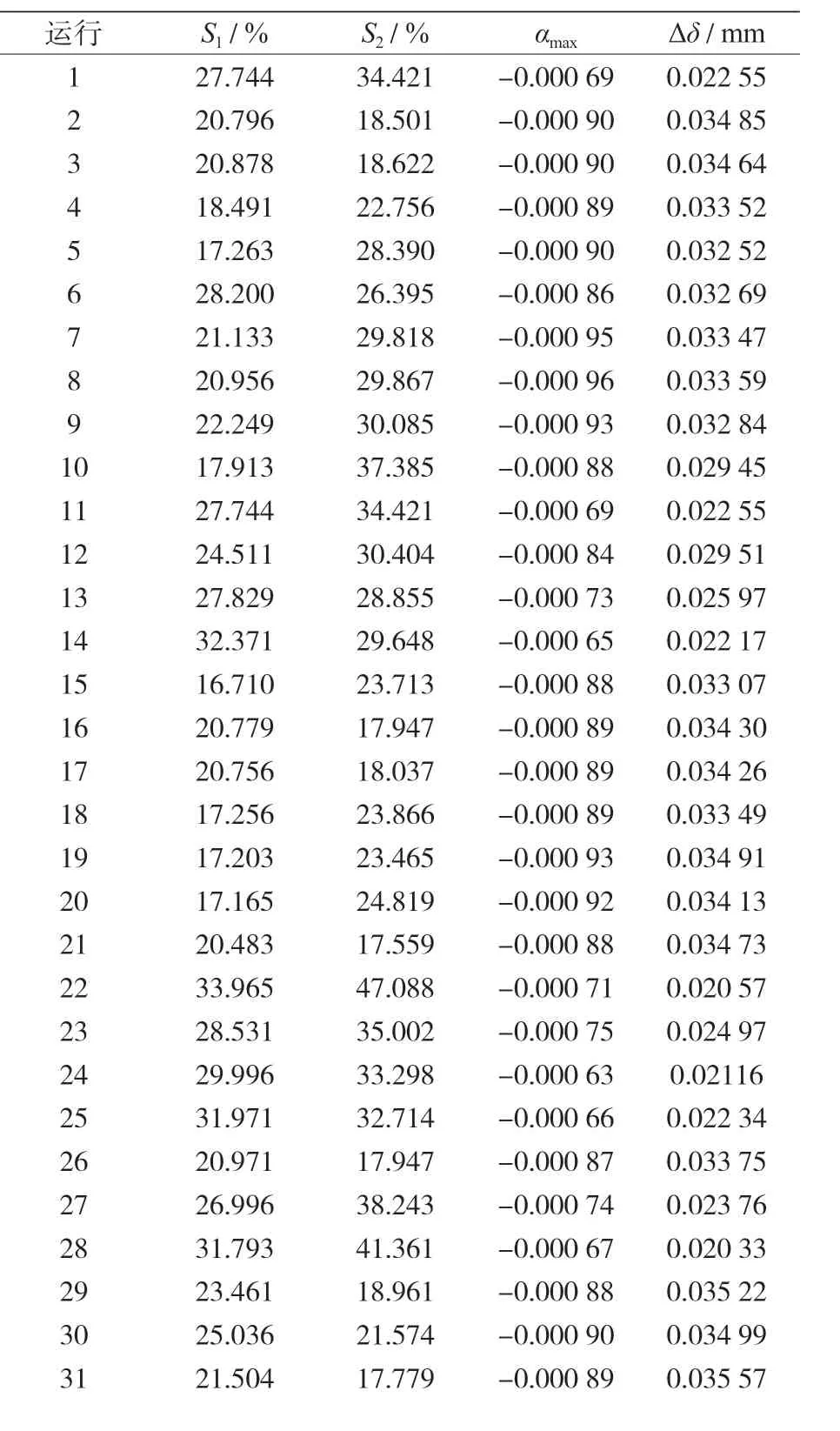
表9 按表8輸入的有FE模擬結果

?

?

3.2 多元分析與無監督分類

實驗進行期間，按照提議四種方法的對數據集的四個變量進行了方差同質性的統計檢驗，表 10 所列的統計數據以及 P 值均為計算值。此外，還進行了相關分析，其結論是：盡管 Fr是最重要的特征，但在當前的實驗條件下，四個特征都具有重要意義。

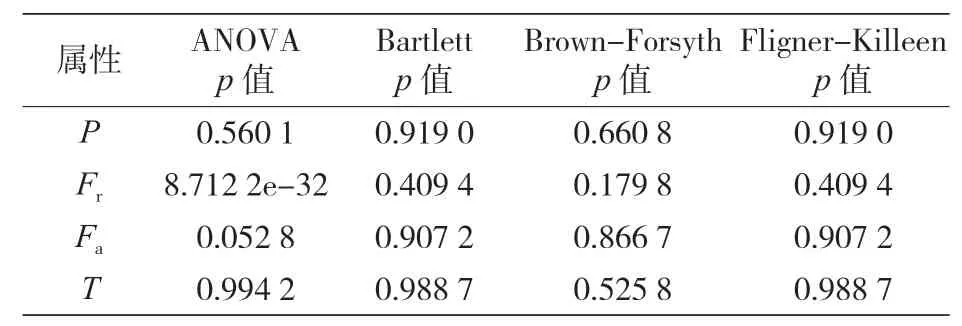
表10 各變量方差均勻性檢驗結果

隨后，將數據集引入 PCA 中，結果表明，所有新的 PCs 所闡釋的數據方差比例（見表 11）與原始特征大致相同。鑒于此，人們認為使用原始特性是更好的選擇，因為使用已知屬性而不是它們的線性組合將構建更容易理解的模型。

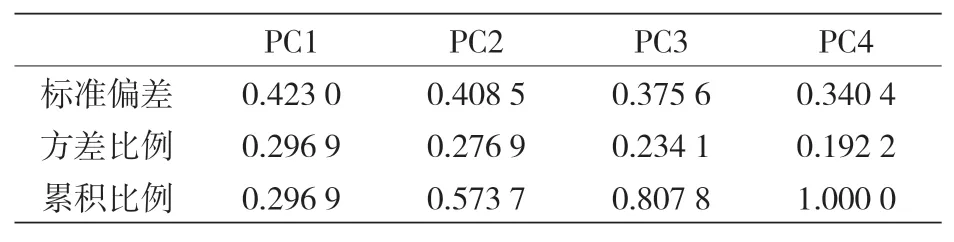
表11 PCs的重要性

從這一點出發，采用無監督聚類方法，根據 4 個原始特征得到 4 組分類。依據 DoE 信息和實例的相似性度量，使用 EM 算法擬合而成高斯有限元混合模型，確定數據的累加是否可以定義和如何定義 4 個集群。對這種無監督算法進行多元混合評價（見圖 5），可以看到，貝葉斯信息準則（BIC）在絕對值上隨著集群數量的增加而顯著增加。進一步的分析結果表明，采用簡單的聚類技術，不能將數據按照誤差較小的類劃分為 4 組。對于一個集群和接下來的 3 個多元混合物（EII、VII、EEI）來說，最好的 BIC 值為343.45。

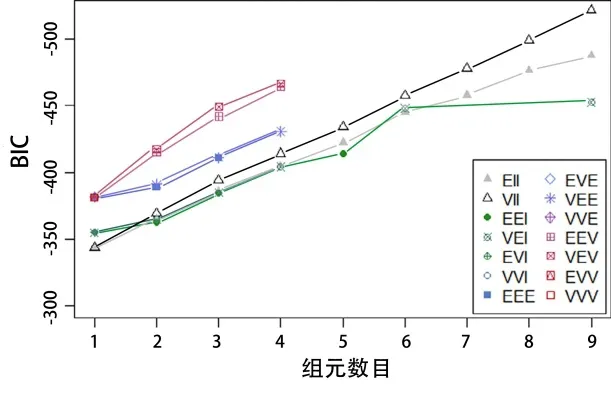
圖 5 集群數與BIC的關系

多元混合體如下：EII（球形、等體積）、VII（球形、等體積）、EEI（對角線、等體積、等形狀）、VEI（對角線、變體積、等形狀）、EVI（對角線、等體積、變形狀）、VVI（對角線、變體積、變形狀）、EEE（橢圓體、等體積、等形狀、同方向）、EVE（橢圓體、等體積、同方向）、VEE橢圓體、等形狀、同方向）、VVE（橢圓體、同方向）、EEV（橢圓體、等體積、等形狀）、VEV（橢圓體、等形狀）、EVV（橢圓體、等體積）和VVV（橢圓體、變體積、變形狀、變方向）。

3.3 分類技術結果

至此，由于采用 PCA 對變量進行特征約簡，以及使用聚類技術對群組進行分類都沒有使分類方法得到改善，因此對所有原始特征進行了監督分類，并利用該方法建立了多個模型，而且利用訓練數據集進行了訓練，同時，在此階段對算法的定義參數進行了優化，提高了算法的精度。表 12 顯示了技術方法、在分析期間已調優的參數、參數的調優范圍以及為最終模型的選用值。一個重復 50 次的十倍交叉驗證過程決定了模型的分類精度，而分析該精度的主要準則為總體精度。但是，如果對誤差百分比有任何疑問，則也要對其他魯棒性準則進行審視。

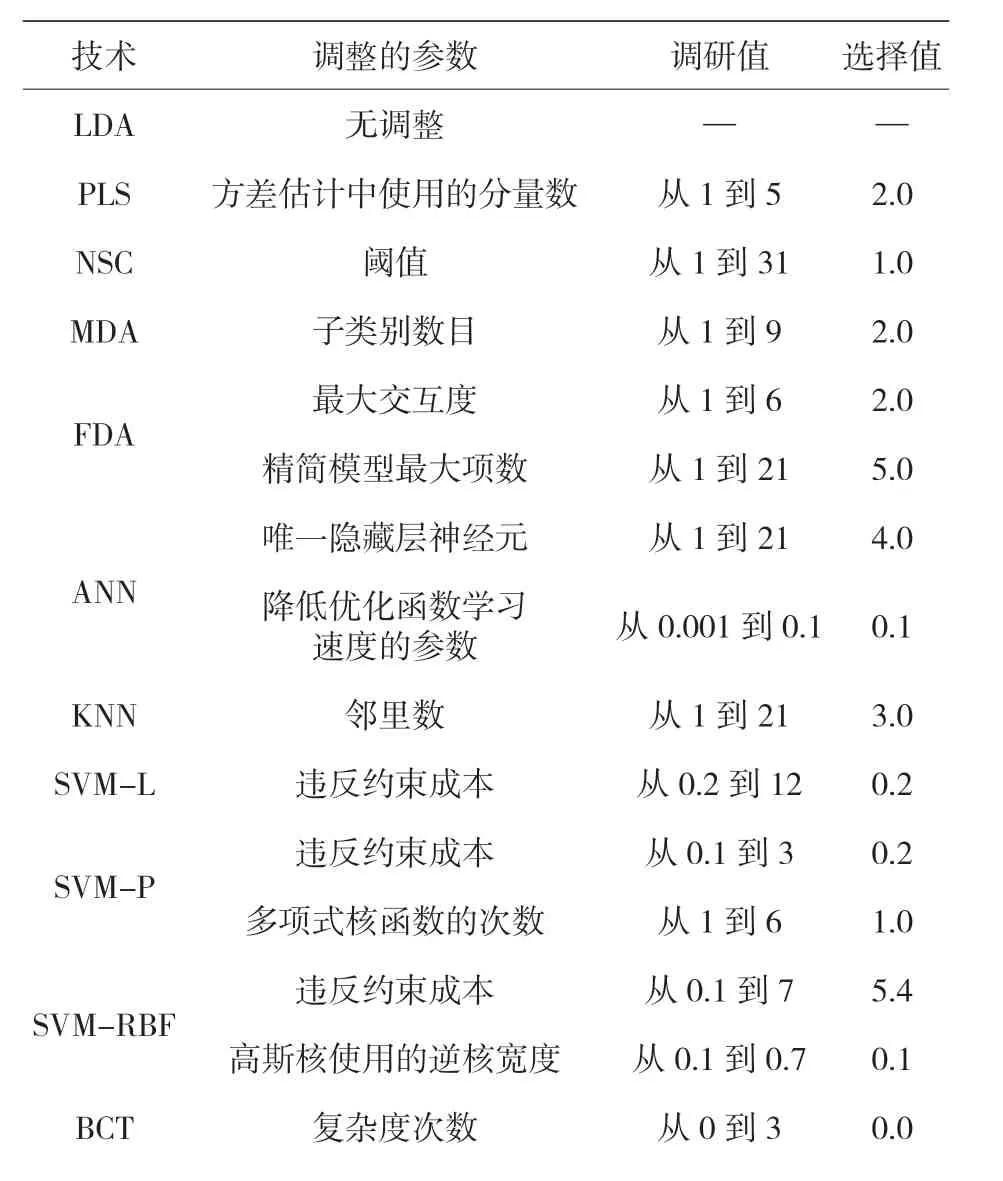
表12 各項技術最重要參數的調整及研究值的選定

?

對每種技術而言，在其最精確模型的訓練階段，都要進行測試，而測試數據集可用來確定每一種方法的實際泛化能力，培訓和測試階段的結果見表 13。這些測試表明，非線性分類方法中的 ANN 和 SVM、分類樹中的 C4.5 和 evTree 以及基于規則的方法等方法在訓練階段都能得到非常準確的結果。然而，當將新的實例應用于模型時，精度要低得多。這一現象說明，在訓練階段，一些模型存在過度擬合，所以測試數據集對分析模型的真實泛化能力非常有用。

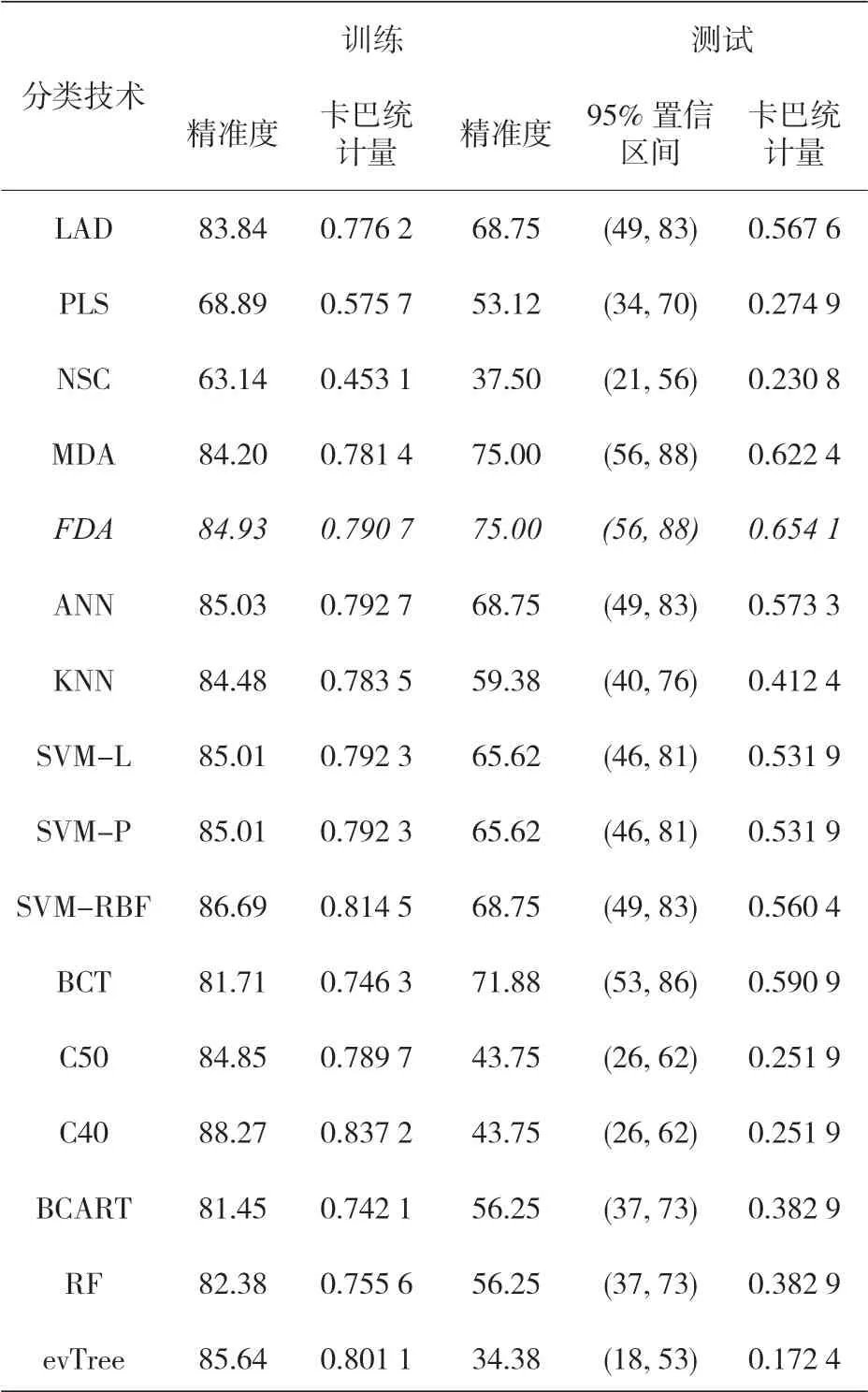
表13 使用所有數據集時，訓練和測試階段的結果（最精確的模型由斜體字表示）

這一具有所有的原始特征并基于 FDA 的模型，在對最佳預設條件進行分類的過程中，提供了最大的準確性，且基于判別分析的不同非線性技術的精度差異也不太顯著，此外，為確定哪個FDA 是最準確，我們可以采用其他建議的標準來判別（例如，對于未加權的 kappa 統計，使用FDA 的價值大于使用 MDA）。

表 14 顯示了使用所選 FDA 模型的測試數據集的混合矩陣，該矩陣表明，“優秀”級別的預測是相當準確的，該級別必須確保 TRB 的正確工作條件。這個預測顯示出每一個被標記為“優秀”的級別是如何被預測為“優秀”的。然而，由于 16 個實例中有 6 個預測錯誤，所以級別被標記為“差”的實例較難分類，而“壞”和“好”級預測了所有標記的實例，只有一個例外。此外，表 15 顯示了分類模型性能的更多統計信息。

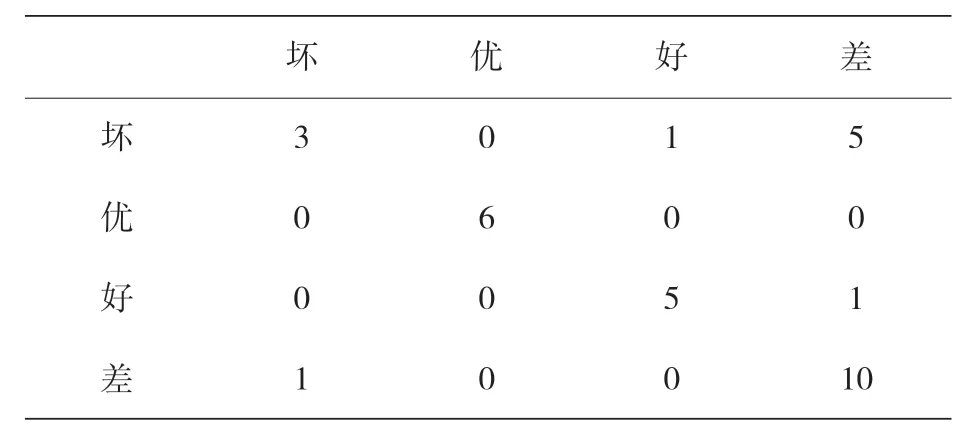
表14 基于FDA的模型在測試階段的混淆矩陣

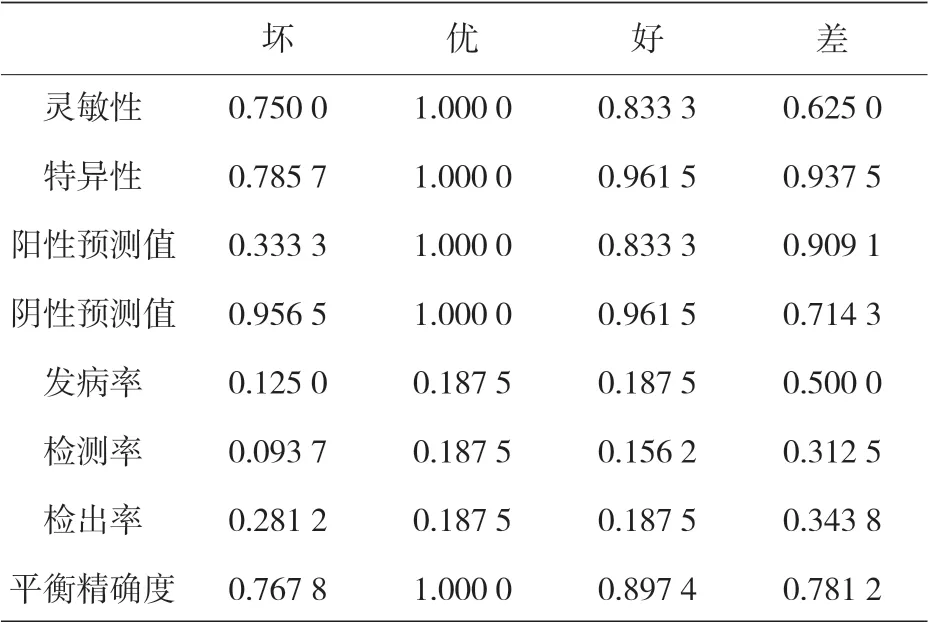
表15 測試階段基于FDA的模型統計

雖然在 FDA 模型中使用測試數據集時總準確率為 75%，但當對這些結果進行分析時，可以看出該準確度可以得到提高。本案例中，可以把所定義的 4 種級別的問題簡化為 2 類，第一類涵蓋原來的“壞”和“差”，它使得 TRB 在不恰當的條件下運行；另一類包括了“優”和“好”，意味著 TRB 在合適的條件下工作。在本例中，表16 中顯示的混淆矩陣表明，只有兩個實例被預測為與其標簽不同的類。這意味著當合并相關類以減少類的數量時，模型的總精度可以提高到 93.75%。

表16 測試階段僅為“壞-差”和“好-優”兩各級別的基于FDA模型的混淆矩陣

FDA 是基于 LDA 的線性技術，但有一個額外的懲罰策略，該懲罰模型采用彈性網絡技術：L1懲罰實際上消除了預測因子，而 L2懲罰降低了判別函數的系數。判別空間構造模型的維數等于 3（θ1，θ2，θ3），解釋模型的方差百分比在各個維度上分別為 66%、29.46%、4.54%，此外，得到的三向維度與原始特征的關系如表 17 所示，它表明在四個原始特征中，只使用了 P、Fr和Fa，沒有使用 T，其中，h（·）為鉸鏈函數，如式（5）所示。表 18 給出了用于判別空間各維度的預測結果。

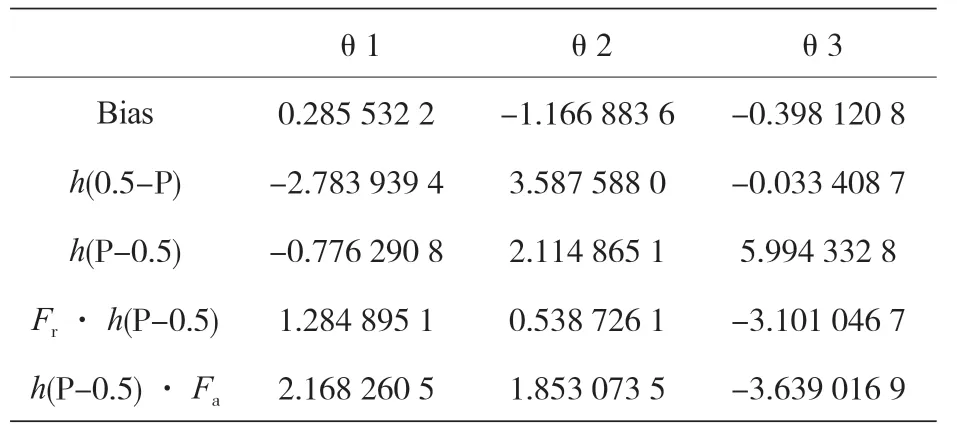
表17 所得3D模型與原始特征的關系

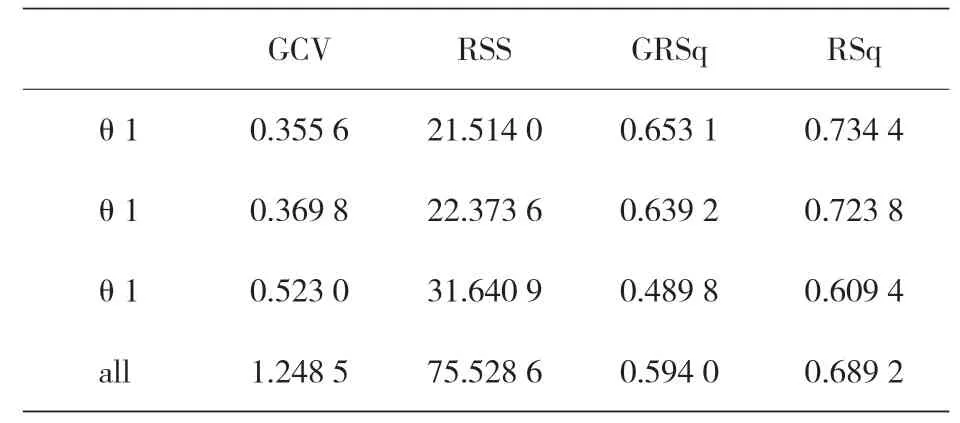
表18 各維和全維度的預測結果

4 結論

本文驗證了一種基于數據分析和機器學習技術的兩步方法，該方法既可應用于有限元模型分析，也可應用于數據挖掘。其目標是創建一個可以自動分類的組合載荷模型，該載荷可以界定一個雙排 TRB 的、與其穩定的工作狀態相關的預置條件。為此，建立了雙排 TRB 的三維有限元模型，并成功地對其進行了數值模擬，且模擬和實驗結果一致。在此模型的基礎上，按照所提出的DoE方法，執行了一個將負載與定義工作條件的類別相結合的數據集，隨后對數據進行統計分析，其中包括探索性分析以及方差和相關性分析，以消除不重要的變量，同時建立了幾種分類模型，并通過特征約簡和參數調優技術對它們進行了優化。為了確定方法的性能，使用了新的實例測試和驗證了優化的模型，結果表明，一些方法在定義可能性空間時產生了過度擬合，但在生成模型時所使用新的實例沒有降低模型的性能。最后，可以看出最精確的模型是在非線性分類方法組內，更具體地說，它是在柔性的判別分析的基礎上產生了 93.75% 的、非常準確的結果，而最初的四個類被減少到只有兩個。結果表明，將有限元法與機器學習技術相結合，可以成功地確定機械裝置的工作狀態。