基于半動態拓撲優化的電網運行方式輔助決策

翁毅選， 馬偉哲， 史軍， 何曉峰， 翟鶴峰， 趙利剛

(1. 深圳供電局有限公司，廣東 深圳，518001；2. 直流輸電技術國家重點實驗室(南方電網科學研究院有限責任公司)，廣東 廣州，510663)

0 引言

傳統電力系統運行中，配電網可通過重構改變運行的拓撲結構[1—3]，而輸電網的拓撲結構除了線路檢修或偶發故障外，通常認為是固定不變的，不考慮其拓撲隨系統運行方式改變而靈活調整。但實際上，輸電網結構是在規劃時考慮的典型或極限運行方式下確定的，留有較大安全裕度[4—5]。而實際系統運行中負荷水平是變化的，因此對于多數運行方式，在不影響電網運行安全性的前提下，可以進一步考慮對網絡拓撲進行優化，從而自適應跟蹤實際系統負荷變化，提升運行經濟性。

輸電網拓撲優化問題[6—9]是對電網運行過程中的網絡結構進行動態調整，靈活地選擇最優的網絡運行拓撲，以改善電網運行中存在的輸電阻塞[10—11]、短路電流超標[12]、電壓越限[13]等問題。實際系統運行中，調度人員可以改變網絡運行拓撲，如春節期間調壓困難時會斷開部分線路使其處于熱備用，從而降低站點電壓。近年來，網絡拓撲優化問題引起了國內外專家學者的廣泛關注和探索研究，諸多研究表明在電力系統運行中根據電網的實際狀況和需求靈活地改變網絡拓撲，將有助于進一步提升系統運行的安全經濟性能[14—16]，文獻[17]也對實施網絡拓撲優化的可行性進行了論述。

文獻[18]對電網結構優化問題進行了綜述，當前網絡拓撲優化方法可分為2類：一類是靜態網絡拓撲優化，即不考慮網絡結構隨時間的變化而變化。文獻[6]首次提出輸電網結構優化的混合整數線性規劃(mixed integer linear programming，MILP)模型；文獻[10]采用網絡拓撲優化進行電網安全均勻調度，改善潮流分布的均勻度；文獻[16]在進行網絡拓撲優化建模時考慮N-1安全約束，從而提升對系統安全性的考慮。靜態網絡拓撲優化方法的優勢在于表征線路開斷與否的狀態變量與時間無關，因此計算效率較高，但缺點在于不能動態跟蹤負荷變化，靈活調整網絡結構。

另一類是動態網絡拓撲優化，即考慮網絡結構隨時間變化而動態變化。文獻[19]考慮網絡拓撲優化用于電力市場出清，并指出該方法可提高市場出清效率；文獻[20]考慮網絡拓撲優化用于機組組合，并指出該方法可以顯著節省運行成本。文獻[21]則同時考慮網絡拓撲優化與N-1約束構建機組組合模型。動態網絡拓撲優化方法的優點在于網絡拓撲隨時間的變化自適應地動態調整，系統運行靈活性好，但缺點在于表征線路開斷與否的狀態變量與時間關聯，計算難度大，計算效率低。

綜上，為優化電網運行方式，兼顧模型解算效率與運行靈活性，提出半動態拓撲優化方法，進而構建一般形式的電網運行方式輔助決策模型。最后，通過算例分析說明了該優化方法的優勢。

1 網絡拓撲優化方法

1.1 現有網絡拓撲優化方法

文中從優化考慮的線路狀態變量與時間的關聯關系角度，將現有網絡拓撲優化方法分為靜態拓撲優化與動態拓撲優化2類。其中，靜態拓撲優化的特點在于優化網絡結構時不考慮隨時間變化，該類方法對應的拓撲約束為[3]：

(1)

式中：L為線路集合；C為最大允許斷開的線路數；zij為表示線路(i,j)斷開與閉合的0-1變量，若斷開則為0，閉合則為1。

由于該類方法的網絡拓撲變化與時間無關，因此不能動態跟蹤負荷與發電，優化所得結果的運行靈活性較差。

動態拓撲優化的特點在于考慮每條線路斷開與否與時間關聯，但各時段間斷開與否無耦合關系，該類方法對應的拓撲約束為[15]：

(2)

式中：T為表征時間周期的集合；zij,t為表示線路(i,j)在時段t斷開與否的0-1變量，若在時段t斷開則為0，閉合則為1。

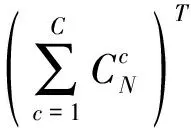
1.2 半動態網絡拓撲優化方法

針對上述靜態與動態網絡拓撲優化方法存在的缺點，文中借鑒文獻[22]所提配電網重構方案思路，即考慮線路在一天內僅進行一次狀態切換，第二日優化則在前一日的拓撲基礎上再次進行優化，提出了一種半動態網絡拓撲優化方法，該類方法對應的拓撲約束可用式(3)表示。

(3)

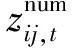
在計算效率方面，文中所提半動態拓撲優化方法的特點在于對系統中的每一條線路，在優化的整個時間周期內僅能改變狀態一次，即假設初始狀態下所有線路閉合，一旦線路某一時段斷開，則在之后剩余的時間段內均保持斷開狀態不變。因此，由式(3)可知，對包含N條線路，T個時段的運行方式優化問題而言，該類網絡拓撲優化方法最大將存在與動態拓撲優化方法相同的線路組合方式，最少將存在與靜態拓撲優化方法相同的線路組合方式，即組合方式介于靜態方法與動態方法之間，因而具有模型求解計算上的優勢。

在系統運行靈活性方面，半動態拓撲優化方法可以在某一關鍵時段切換線路狀態，并保持后續線路狀態不變，因此也具有一定的運行靈活性。此外，對運行管理人員來說，每天只需要根據日前決策的線路開斷結果對線路開關操作一次，操作簡便；同時，對線路開關而言，不會像動態方法那樣造成線路開關頻繁動作，因此有利于延長開關使用壽命。

另外，需要說明的是文中所做的初始狀態下所有線路均閉合的假設并不影響模型的適用性，對于實際中不能參與開斷的線路或者處于檢修狀態已斷開的線路只需要固定其對應的線路狀態變量為1或0即可。為更好地說明3類網絡拓撲優化方法的區別，圖1給出了3類方法對應的線路狀態變量z的可取值示意，可以更加直觀地看出3類方法在變量數目和組合方式上的差異。

圖1 3類網絡拓撲優化方法對應的線路狀態變量Fig.1 Schematic of line state variables corresponding tothree types of network topology optimization methods

2 基于拓撲優化的電網運行方式輔助決策

基于上章所提網絡拓撲優化方法，以電力系統日前運行方式輔助決策問題為例，計及網絡拓撲優化構建一般形式的電網運行方式輔助決策模型。其中，目標函數為日前所有發電機組的發電出力成本最小；約束主要包括機組出力范圍約束、爬坡速率約束、潮流約束、傳輸功率約束、備用約束以及上節所述網絡拓撲約束。

2.1 目標函數

(4)

式中：G為發電機集合；ag，bg，cg分別為機組g發電成本函數的二次、一次和常數項；Pg,t為機組g在時段t的有功輸出功率。式(4)所示目標函數即為發電機組有功出力對應的二次成本函數，即最小化整個系統的發電成本。

2.2 約束條件

(1) 機組出力上、下限約束。

(5)

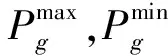
(2) 機組爬坡速率約束。

(6)

(7)

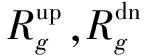
(3) 線路傳輸容量約束。

(θi,t-θj,t)/xij-fij,t+(1-z)M≥0
?(i,j)∈L,t∈T

(8)

(θi,t-θj,t)/xij-fij,t-(1-z)M≤0
?(i,j)∈L,t∈T

(9)

(10)

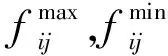
(4) 節點相角約束。

(11)

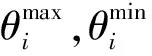
(5) 節點功率平衡約束。

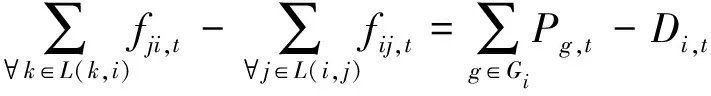
(12)

式中：Di,t為節點i在時段t的負荷量；對線路(k,i)，k∈L(k,i)表示與節點i相連且末端節點為i的線路構成的集合；同理，j∈L(i,j)表示與節點i相連且始端節點為i的線路構成的集合。

(6) 備用約束。文中在進行運行方式輔助優化時僅考慮系統正常運行所需要的旋轉備用，以應對負荷及新能源出力波動帶來的影響，暫不考慮偶發故障所需的事故備用約束。

(13)

(14)

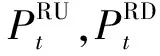
(7) 網絡拓撲約束。即式(1)或式(2)或式(3)約束。采用不同的網絡拓撲優化方法，需選擇相對應的約束式。

易知，上述基于網絡拓撲優化的電力系統日前運行方式輔助決策模型除了目標函數為二次函數外，約束條件均為線性，屬于混合整數二次規劃問題，雖然現有求解器也可直接對此類問題進行求解，但計算效率相對較低，因此下節將介紹線性化方法將目標函數線性化，從而將模型轉化為MILP模型進行求解。

3 模型轉化與求解

機組的發電成本為二次函數，為減輕模型求解難度，將其采用插值線性化方法[23]線性近似表示。

(15)

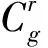
上述線性近似方法須同時滿足以下約束條件：

(16)

(17)

(18)

(19)

(20)

易知，通過上述轉化，文中基于網絡拓撲優化的電力系統運行方式輔助決策模型已轉化為MILP模型。

此外，考慮到應用于實際大系統時，現有求解器直接求解大規模MILP問題仍存在效率低下的問題，文中提出采用Benders分解法求解大規模算例系統。Benders分解法的實質是將一個大規模但僅需求解一次的問題，分解成一系列的小問題反復迭代求解的方法，其示意如圖2所示。

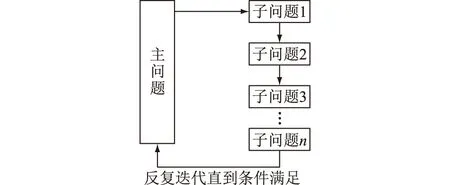
圖2 Benders分解法示意Fig.2 Schematic diagram of Benders decomposition

將上述MILP問題表示為矩陣的一般形式為：

(21)

式中：y為表征模型中0-1變量相關的變量；x為表征模型中連續變量相關的變量；A，B為約束中相關的系數；c,f為目標函數中的相關系數。

(22)

式中：p為引入的對偶變量。

當求解子問題后，根據判斷結果添加約束至主問題進行求解再次得到新的0-1變量y。然后反復迭代求解，直至收斂。主問題的對應形式為：

(23)

式中：i為迭代次數。

主問題實際上是原問題的一個松弛問題，計算后可得到主問題的目標函數，比原問題更優，因而是原問題目標函數下界。隨著迭代進行，當上界與下界差足夠小時，迭代停止。實際應用中，往往添加較少的約束就能很快收斂。

4 算例分析

以IEEE 14節點[24]、IEEE 118節點[6]系統為例，對半動態拓撲優化方法與靜態和動態拓撲優化方法進行對比測試。編程基于GAMS Studio 27.3軟件，調用CPLEX求解器進行MILP問題的求解，測試中所設置的CPLEX求解器的相對最優解收斂標準OptCR為0.1%，測試計算機配置為Intel(R) Core(TM) i5-6300U系列CPU，主頻2.4 GHz，內存8 G。

4.1 IEEE 14節點系統

測試采用的IEEE 14節點系統中共有5臺發電機，20條線路，對應的機組和線路參數分別見表1和表2。

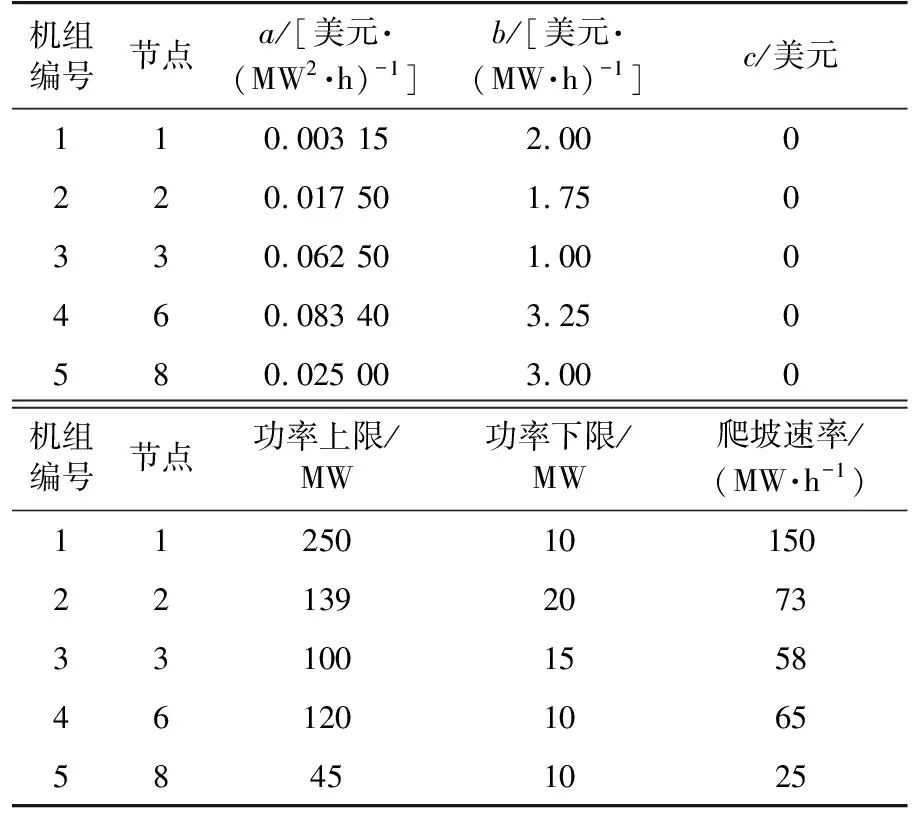
表1 發電機組參數Table 1 Parameters of the generators

此外，文中電力系統運行方式輔助決策問題考慮的時間間隔為1 h。測試系統中各節點負荷及日前的負荷預測變化情況如表3與表4所示，同時，測試中目標函數采用插值線性化方法表示時選取的插值點數為6。

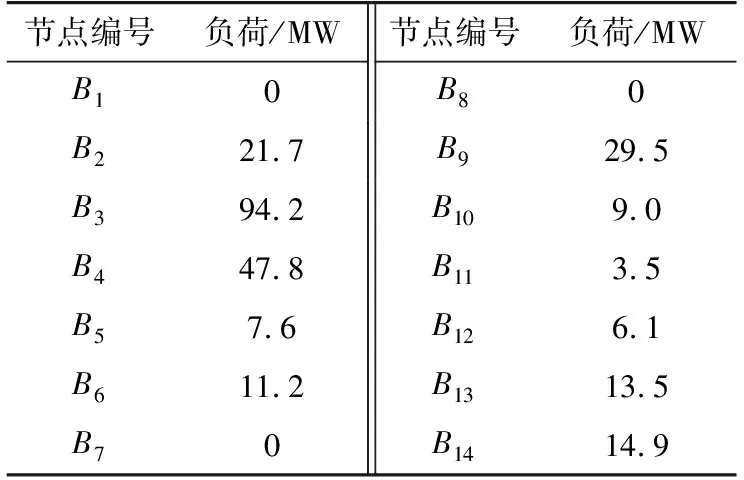
表3 節點負荷參數Table 3 Parameters of the bus load

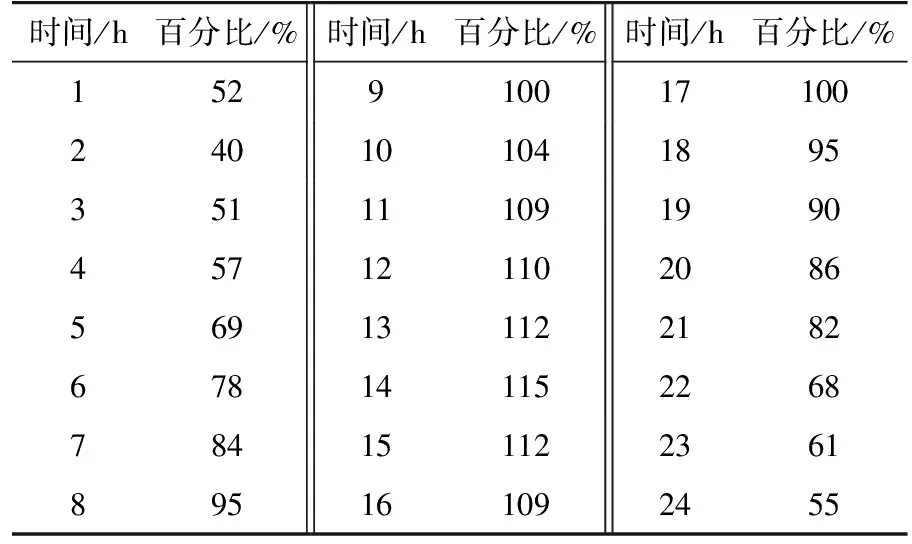
表4 節點負荷變化參數Table 4 Parameters of the bus load variation

4.2 靜態網絡結構優化對應結果

首先采用靜態網絡拓撲優化方法，對電力系統運行方式輔助決策模型進行求解，當網絡結構允許改變的最大線路數C取不同數值時對應的目標函數及網絡拓撲結果如表5所示。

表5 靜態網絡結構優化對應的目標函數及拓撲結果Table 5 Objective function and network topology resultscorresponding to static network topology optimization

由表5可以看出，當斷開的線路數小于等于2時，隨著系統允許斷開的線路數增加，系統的運行成本逐漸減小，之后再增加斷開的線路數量系統的運行成本不再減少。這說明在此種網絡結構優化方法下，網絡的阻塞已經得到了最大程度的緩解，經濟性好的機組功率輸出能力已得到較為充分的利用，系統運行的經濟性無法再通過此種手段得到進一步優化。

4.3 動態網絡結構優化對應結果

采用動態網絡結構優化方法，應用于電力系統運行方式輔助決策模型，當網絡結構允許改變的最大線路數C取不同數值時，求解模型所得到的目標函數及網絡拓撲結果如表6所示。

表6 動態網絡結構優化對應的目標函數及拓撲結果Table 6 Objective function and network topology results corresponding to dynamic network topology optimization

由表6可以看出，與靜態網絡拓撲優化方法不同的是，隨著系統允許斷開的線路數增加，系統的運行成本逐漸減小，而且即便是允許斷開線路數相同的情況下，動態網絡結構優化方法可以靈活適應源-荷變化，從而可以充分發揮經濟性較好機組的出力能力，所以經濟性能提升更加顯著。此外，因為系統在不同的負荷水平下網絡中起關鍵阻塞作用的線路是不一樣的，通過靈活地改變網絡結構可以最大程度上減輕網絡的阻塞程度，提升運行經濟性。

4.4 半動態網絡結構優化對應結果

將文中所提半動態網絡拓撲優化方法應用于電力系統運行方式輔助決策模型，當允許改變的最大線路數C取值變化時，求解模型得到對應的目標函數值及網絡拓撲結果如表7所示。

表7 動態網絡結構優化對應的目標函數及拓撲結果Table 7 Objective function and network topology results corresponding to semi-dynamic network topology optimization

由表7可以看出，無線路斷開時，半動態網絡拓撲優化方法與靜態和動態方法對應的目標函數均一致，說明了文中所構建模型的普適性。當允許斷開的線路數為1時，半動態網絡拓撲優化方法對應的目標函數與靜態方法相同，高于動態方法，這表明此時半動態方法所能提升的經濟性效果與靜態方法相同，靈活性差于動態方法；當允許斷開的線路數為2時，半動態網絡拓撲優化方法對應的目標函數低于靜態方法，高于動態方法，這表明此時半動態方法所能提升的經濟性效果優于靜態方法，靈活性雖差于動態方法但優于靜態方法；當允許斷開的線路數為3時，與靜態方法不同，半動態方法對應的目標函數進一步減少，這表明此時半動態方法可以在一定程度上進一步減輕系統的阻塞程度，發揮經濟性較好機組的出力能力，運行靈活性明顯優于靜態方法。

通過上述算例對比分析可知，文中所提半動態網絡拓撲優化方法可以在不損失靜態方法改善系統阻塞程度的前提下進一步減輕系統的阻塞，提升運行的經濟性。

4.5 計算效率對比

采用IEEE 14節點與IEEE 118節點系統對上述3類網絡拓撲優化方法對應的運行方式輔助決策模型計算效率進行測試，當允許斷開的線路數C取值由小變大時，3類方法對應的模型計算時間如表8所示。

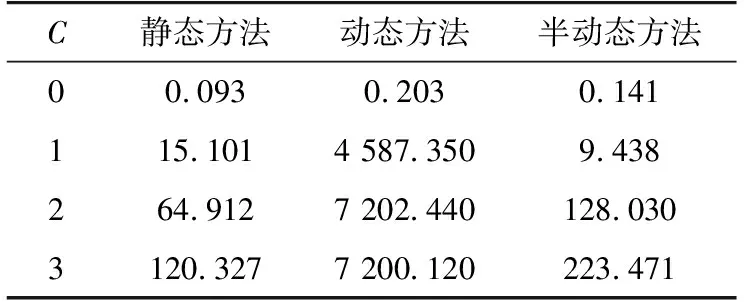
表8 IEEE 14節點系統3類方法計算時間Table 8 Computation time of three kinds of methods of IEEE 14 bus system s

需要說明的是，對于IEEE 14節點系統規模較小時采用直接求解MILP問題的方案，對于IEEE 118節點系統規模較大的情況下采用Benders分解法求解的方案，Benders算法所設置的收斂標準為上下界目標函數差小于等于0.1。此外，為了在一定時間內獲得模型的有效解，采用文獻[25]所提啟發式方法，通過限定模型的最大求解計算時間為2 h(即7 200 s)，從而獲得模型的次優解。

由表8可以看出，3類方法中靜態方法具有較高的計算效率，且隨允許斷開線路數目的增加，計算時間變化并不顯著。然而，對動態方法而言，由于線路組合情況隨時間呈指數級增長，因此即便在開斷線路數目為1的情況下，計算時間也接近1 h，而當開斷線路數目為2或者更多時，模型求解在2 h內無法獲得最優解，僅僅得到次優解，由此也說明了該類方法為提升網絡運行靈活性而帶來的計算效率低下的問題。對于文中所提半動態方法而言，隨著允許開斷線路數目的增加，模型的計算時間增長較快，但即便在線路開斷數目為3的情況下，模型計算時間仍在4 min，說明文中所提半動態方法不僅可以兼顧系統運行靈活性，提升系統運行經濟性，而且具有較高的模型解算效率。

由于IEEE 14節點系統在C為2時動態方法求解時間已達到上限(2 h)。因此對IEEE 118節點系統的模型解算效率進行測試時，采用Benders分解方法，測試結果見表9。

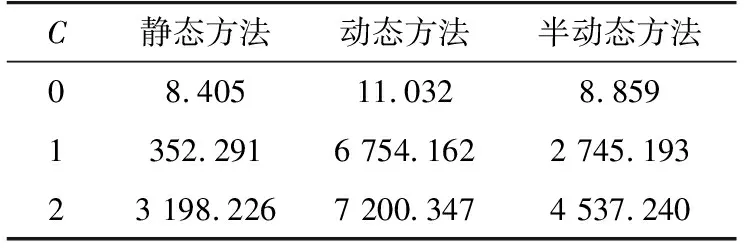
表9 IEEE 118節點系統3類方法計算時間Table 9 Computation time of three kinds of methods of IEEE 118 bus system s

通過表9可以看出，當采用Benders分解算法時，對IEEE 118節點系統，當C取0～2時，靜態方法和半動態方法均可在限定的2 h內求解內完成求解獲得最優解。然而，對于動態方法，在C取2的情況下只能在限定的2 h內獲取次優解。由此說明了半動態方法計算上的顯著優勢，具有實際應用的可能性。

5 結論

文中首先對電力系統的靜態與動態網絡拓撲優化方法的優缺點進行闡述，進而提出了半動態網絡拓撲優化方法，并構建了電網運行方式輔助決策的一般形式的數學模型，通過算例對比分析表明：

(1) 根據電力系統運行狀態，基于網絡拓撲優化方法輔助決策電網運行方式，可以減輕電網存在的阻塞，將有助于進一步提升電網運行的經濟性和魯棒性；

(2) 3類網絡拓撲優化方法中，半動態網絡拓撲優化方法的運行靈活性較靜態網絡拓撲優化方法優，提升系統運行經濟性的潛力更大，但次于動態網絡拓撲優化方法；

(3) 基于半動態網絡拓撲優化方法所構建的電網運行方式輔助決策模型的解算效率較動態網絡拓撲優化方法優勢明顯，且略低于靜態網絡拓撲優化方法，具有實際應用的可能性。