應用聚類算法的大壩安全監控方法

黃海兵，吳云星，谷艷昌

(1.南京水利科學研究院，江蘇 南京 210029；2.水利部大壩安全管理中心，江蘇 南京 210029)

隨著水利工程建設的不斷推進，它在國家經濟民生中發揮著越來越重要的作用，特別是高壩大庫的發展，使得水庫大壩不僅在防止洪澇等民生安全方面起到了巨大的保障作用，也在發電等方面發揮著巨大的經濟效益。而這一切的基礎即是大壩能安全運行，所以對大壩進行運行性態分析就顯得尤為重要[1]。普遍地，為了更加全面監測大壩的運行性態，通常是在壩體上布設更加系統化的監測測點，以獲取更加全面的監測數據資料，繼而監測大壩的各項運行指標。然而數據資料太多又會導致分析處理繁瑣的問題，若對海量的監測數據資料進行逐一分析，這不僅耗時耗力，也不利于及時得到有效的信息以迅速對大壩的運行狀況進行評價[2]。因此，就需要對海量的數據進行深度的挖掘，從中找到數據之間隱含的、有價值的、能理解的趨向與關聯，進而降低數據分析復雜度，提高大壩管理者的分析、決策能力[3]。聚類算法作為一種數據挖掘中廣泛運用的機器算法，它解決的難題是把一個數據集合重構為若干個子集。而且每個子集在依據原則下具有一定的相似性，并在不同子集間具有盡可能大的相異性[4]。

目前，聚類已成為在遙感、客戶關系管理、醫學、市場營銷、電信、軍事、商業領域和金融等領域中常用的統計數據分析技術[5-9]，但在大壩監測資料分析中應用的綜合性研究論述還比較少。因此，本文首先闡述數據挖掘中聚類算法的發展及其研究現狀，然后論述聚類算法在大壩安全監控領域中應用內容及成果，最后討論大壩安全監控應用聚類算法需要關注的關鍵問題，以供相關人員參考學習[10]。

1 聚類算法的發展

隨著大數據時代的蓬勃發展，聚類算法在日益增加的數據量與日益多樣化的數據形態的處理分析中變得越來越廣泛，這也促使了一系列不同特點的聚類算法的發展，以滿足各式各樣數據類型的處理要求。聚類算法一般可分為傳統聚類[11]、模糊聚類[12]以及智能聚類[13]。

1.1 傳統聚類方法

傳統聚類算法主要有以下4種劃分：[14]。

(1)劃分聚類法

該聚類算法的基本思路是利用分裂的方式把一個由n個元組組成的集合分割為k個類別，每一個類別有且僅包含一個對象。現假設集合C:

C={X1，…，Xi，…，Xn}，Xi=(xi1，…，xid)

(1)

式中，Xi—樣本點；Xid—該樣本的屬性、特征、變量等，有d個維度。

使用此類劃分思想的代表性算法包括k-means(由其質心作為聚類中心，對極值很敏感)、k-medoids(由其中位數作為聚類中心)、EM、CLARA、CLARANS等。基于劃分的聚類的優缺點都十分明顯，其優點主要體現在收斂速度快，模型參數少(僅有一個聚類中心數k)，并且當類間區分明顯時，劃分效果好；其缺點即為數據類型適應性差，僅能用于定義平均值的數據類型，受聚類中心數的影響較大，聚類的好壞完全受到k的影響。

(2)密度聚類法

基于密度的方法最主要的特點就是對數據集合進行處理，如果某區域點的密度超過了設定的限值，則把該點歸之鄰近的其他類別中。其中密度聚類算法最有代表的為DBSCAN算法，其核心是該算法的每一個簇為所有連續密度數據的最大集合。馮少榮[15]針對DBSCAN算法中對輸入參數敏感、運行內存量大等缺點，提出算法參數的動態變化以適應結果要求，并且采用并行化處理對數據進行劃分，從而提高聚類效率，降低內存要求。

此外，還有OPTICS、DENCLUE等基于密度的聚類，OPTICS能夠有效改善DBSCAN對與輸入參數領域E等的敏感性，而DENCLUE是根據確定的密度分布函數進行聚類分析。

(3)網格聚類法

網格聚類方法的特點在于其處理速度與點集合對象的個數無關，只和網絡結構的各個維中的單元個數有關，以此具有較高的計算速度。基于網格結構的劃分可根據劃分方向分為自底向上劃分網格和自上而下劃分網格兩種。

其中CLIQUE、STING、Wave Cluster等是網格聚類的典型。此外，網格聚類往往會和其他方法相嵌合運用，且和密度聚類算法嵌合最多，從而衍生出一系列綜合類算法，如SCI、MAFIA、DCLUST、GCHL等。

(4)層次聚類法

基于層次的方法顧名思義在對數據進行聚類處理的時候，會形成一個類似二叉樹的結構，對集合進行層次似分解，最后只剩下一個大類結束。層次聚類構造樹的形式有凝聚法和分裂法。

其中AGNES、BIRCH、CURE等是凝聚法手段的代表；而分裂法就是自上而下法，它推求將所有的對象置于一類，不斷細分為更小的類，DIANA等是其主要代表。

1.2 模糊聚類方法

傳統的聚類是屬于一種“硬”聚類方法，它的判定規則為0與1，即對象間有清晰的分解。但實際上，許多對象的要素無法有一個精準的表示，所以模糊聚類方法就應運而生。

目前，模糊聚類算法的種類繁多，而應用最廣泛的是依據目標函數的模糊聚類，此類分析算法將聚類看作為一個有限制條件的非線性問題，進而轉化為解決問題的最優化來完成對集合的聚類。而在眾多基于目標函數的聚類算法中，Bezdek[16]于1973年創立的模糊C-均值聚類(FCM)理論是典型的代表。

FCM算法有一個最顯而易見的缺點，即它的性能取決于初始聚類中心，優化結果通常會陷入局部最優，并非全局最優[17]。解決思路一般有兩類，一類是在每個初始聚類中心進行計算，然后多次迭代FCM算法，直到符合結果條件。一類是通過蛙跳、粒子群、遺傳算法等優化算法進行計算初始聚類中心。以第二類為基礎發展而來算法就是智能聚類算法。

1.3 智能聚類方法

智能聚類主要有：人工神經網絡聚類、核聚類和智能搜索聚類等。

(1)人工神經網絡聚類

人工神經網絡通過模擬人類大腦的神經系統而得名，它具有很強的非線性逼近能力，可以適應各種由傳統數學模型無法描述的復雜系統，從而可以很好地應用于模式分類。自組織神經映射(SOM)[18]是應用人工神經網絡實現聚類的目的。該方法能夠對數據進行無監督學習聚類，將高維空間上的點映射到低維空間，并保持數據點間的距離和鄰近關系一定，從而實現可視化。此外，還有改進的SOM算法和基于投影自適應諧振理論的人工神經網絡聚類[19]。

(2)核聚類

核聚類采用支持向量機中的核函數。該聚類依據Mecer理論，進行核變換，將數據集的低維度樣本映射到高維度，使之被較好地處理、分析并增顯有效的要素，最后完成聚類[20]。將輸入空間樣本Xi∈R通過某種非線性映射φ到某一特征空間，x→φ(x)，一般通過Mercer核表示為：

K(xi，xj)=(φ(xi)，φ(xj))

(2)

式中，K(xi，xj)—Mercer核函數；φ(xi)、φ(xj)—樣本xi和xj在高維特征代間中的像。

核函數是定義低維與高維的映射規則，目前應用較多的有高斯核函數、多項式核函數和線性核函數等。

(3)智能聚類

智能聚類，是指運用智能方法搜索解空間的啟發式聚類算法，通過一些智能優化算法，以聚類問題中評價函數為目標函數，搜尋聚類問題的全局最優解，避免了傳統聚類方法容易陷入局部最優的問題，加快收斂速度，降低一些聚類算法對初始值的敏感度。用于聚類問題的代表性啟發式算法有：模擬退火算法、遺傳算法、蛙跳算法、粒子群算法、灰狼算法等。

2 聚類算法在大壩安全監控中的應用現狀

由于傳統聚類算法在大壩安全監控中應用的研究成果和綜述文獻[21]非常多，所以本文重點對模糊聚類算法和智能聚類算法在大壩安全監控中的應用進行展開闡述。

2.1 模糊聚類算法

為了提高監測資料的分析效率，諸多學者將基于模糊數學的聚類分析方法應用到大壩監測資料的分析中。模糊聚類分析法大致可分為兩種[22]：

(1)系統聚類分析法

系統聚類分析是基于模糊關系的聚類算法，其基本操作流程為：首先選定系統中具有實際意義和強解釋性的代表性指標如水頭、氣溫、時效等荷載集以及變形、裂縫開度、應力應變等荷載效應集；然后將各樣本點的統計指標進行標準化處理，消除量綱的影響，便于比較分析；其次進行標定，計算出分類對象間的相似程度的統計量，用模糊相似矩陣表示：

(3)

式中，rij=R(xi，xj) (i，j=1，2…，n)—兩對象之間的相似程度。可采用歐氏距離、數量積法、相關系數法等進行計算。

給定不同的閾值λ，若rij≥λ，則xi，xj被聚類一類。根據不同閾值，得出動態聚類結果[23]。其中廖鋮等人[24]，根據模糊聚類方法，對水布埡面板堆石壩的面板撓度變形監測數據進行分析，根據相關系數法建立測點間的模糊相似矩陣，并采用二次法構造模糊等價矩陣，根據不同閾值，得出動態聚類結果，隨后采用F統計量評價聚類效果以確定最佳聚類結果，通過對關鍵面板的詳細分析，具有較高的擬合度。因此采用模糊聚類分析法處理大壩監測資料能夠在掌握大壩運行狀況前提下，減少了工作量，提高了分析效率。賈彩虹等人[25]，采用灰色關聯度法建立新安江大壩部分壩段壩基時序揚壓力值的關聯相似矩陣，并以此構造模糊相似矩陣，同時基于測點測值的變化規律，對各壩段揚壓力依據相似度來進行聚類，繼而實現以已知預測未知的目標，并以此預測同類壩段壩基揚壓力值，預報結果精度較高。

(2)逐步聚類分析方法

系統聚類方法能夠一次形成分類，但缺點是數據太多，計算量較大。而逐步聚類分析則是對數據進行迭代分級，計算不同級別下各個特征因子的“聚類中心”，該方法可對預報日進行因變量的預測[26]。逐步模糊聚類通常采用模糊劃分，即樣本j以某一從屬度uij從屬于第i類，然后根據公式不斷迭代求得滿足要求的最佳軟分劃矩陣和聚類中心，最后采用直接劃分或者二次分類方法求得樣本所屬類別。

2.2 智能聚類算法

(1)基于SOM神經網絡的聚類算法

Kohonen聚類算法通過競爭型無指導方式而構造的神經網絡來對樣本中的點分析計算分類。所謂競爭型即是“勝者為王”，無指導即是模型無期望[27]。該方法具有兩個主要特點：它是一種遞增的方法；它能將聚類中心點映射到二維平面上而實現可視化。

陳悅等人[27]選取某特高混凝土雙曲拱壩大壩測點變形值的“相對距離”和“增速距離”作為評價數據，采用Kohonen聚類算法訓練模型，挖掘測點時空數據的相似性，識別大壩變形監測點的空間聚集情況，體現了壩體變形的空間特征，聚類結果與實際情況相符，并對聚類結果中的典型測點進行分析，在考慮各測點變形序列的空間關聯性同時，減少工作量，提高分析效率。此外，Kohonen聚類分析還可以探測時空分布中出現異常情況的測點以及利用測點變形的規律性進行同類數據的缺失性填補。

(2)基于螞蟻覓食的聚類算法

蟻群算法具有顯著的全局優化能力。其他學者在此基礎上，與聚類的思想相結合，發展出了于蟻群的聚類算法[28]。如果把數據樣本處理成不同屬性的螞蟻，聚類中心則為螞蟻要覓得的“食物源”，那么分析聚類可以形象地比作螞蟻覓食[29]。

假設數據對象為：

X={X|Xi=(xi1，xi2，…，xim)，i=1，2…N}

(4)

式中，i—樣本數；m—樣本維度，算法初始化操作，則τij(0)=0，設置簇半徑以及誤差等參數，計算對象間的距離dij，則各路徑上的信息素為[30]：

(5)

式中，r—聚類半徑。

其中黃瀟霏等人[31]采用RBF神經網絡，將影響大壩變形的主要因素作為輸入，變形量作為輸出，建立大壩監控模型，同時采用蟻群覓食聚類算法應用與徑向基神經網絡函數中心向量的選擇，使得樣本集內的向量距離該中心的距離最小，以改善大壩監測模型的預測效果。

(3)基于粒子群的聚類算法

該算法是Omran等人于2002年提出的一種聚類算法。除基本粒子群聚類算法外，還有與k-means、模糊C均值算法相結合的混合算法。試驗表明，混合算法在處理聚類問題時好于傳統算法的有效性評價指數，并減小陷入局部最優概率，提高收斂速度[32]。

其中王偉等人[33]利用粒子群優化算法全局搜索能力強、調整參數少、易于實現特點，將模糊聚類算法中的計算條件轉換為優化問題，在全局最優情況下的模糊劃分矩陣以及聚類中心向量，并據此劃分待測樣本的歸類，輸出樣本的預報區間，并以新安江攔河壩的位移作為計算數據并將其進行劃分，根據各影響因子建立模糊矩陣，對待測樣本進行位移的區間預報。

2.3 不同聚類算法的比較

由上述聚類算法在大壩安全監控應用的相關分析可知：不同聚類算法的適應情況不同，一般從收斂速度、初值敏感性、抗噪性能及結果精度比較3種聚類算法的優劣勢，具體對比內容見表1。

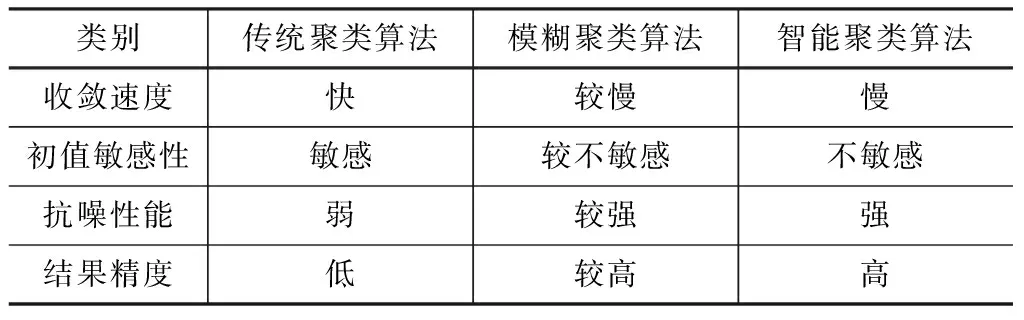
表1 三種聚類算法的比較

3 大壩安全監控應用聚類算法的關鍵問題

采用聚類算法進行大壩安全監控分析，有核函數的選擇、分析精度和分析效率的權衡等關鍵問題。

3.1 核函數

核函數作為聚類算法的控制函數，因變量的輸入離核函數中心越遠，中間層的激活程度就越低，這就使得隱層節點中心和基函數寬度的確定會直接影響算法的收斂速度。所以為改善大壩監測模型的預測效果，有必要采用聚類算法確定合適的隱層節點中心與核函數寬度。因此，對于解決大壩不同的安全問題選擇合適的核函數就尤其重要。

3.2 分析精度

聚類算法因其較高的精度在大壩安全監控中應用較多。由于不同壩型和大壩不同的因變量核效應量需要不同的精度要求，當然在考慮效率的前提下分析精度越高越好。而通過一些改進算法和模型可以看出：在提高精度的時候，會出現小范圍的過擬合以及整體誤差滿足但結果不當等情況。為提高大壩安全監控的分析精度而優化改進聚類算法時，短期分析應注重結果精度要求，長期分析應注重大壩運行趨勢規律。

3.3 分析效率

由于計算機技術的進步，各種用于大壩安全分析的算法越來越多，其中聚類算法也得到了長足的發展。在不同大壩安全分析的項目上，各種改進優化的聚類算法各有優缺點。不少改進優化的聚類算法提高了結果精度，但同時使得分析模型過于復雜，操作性難，實現效率低，給現場工程管理應用人員帶來困難。因此，建立簡單實用的優化聚類算法，構建標準化分析模型以提高分析效率是大壩安全監控的關鍵問題之一。

4 結語

本文對一些常用的傳統聚類方法、模糊聚類方法以及智能聚類方法及其研究現狀進行了簡要介紹，然后詳細闡述了應用于大壩安全監控領域的模糊聚類方法和智能聚類方法以及應用方式。其中模糊聚類方法有較高的擬合度及大幅度減少運算工作量；智能聚類算法結合神經網絡、智能群算法等方法在大壩的前期的資料分析以及監控模型的建立中降低了陷入局部最優的概率，提高了結果精度和穩定性。這表明聚類方法在水工領域中有著廣泛的應用與較大的潛力，對從業人員結合聚類算法進行大壩安全監控研究具有指導意義。

由于目前所涉及的應用于大壩監控領域的聚類方法是常規的應用，如何將模糊聚類算法及智能聚類算法更好地結合大壩動態監測資料分析或實時監控模型的建立，需要進一步深入研究。