基于自適應匹配追蹤算法的齒輪箱軸承故障特征提取

李有新

(青海高等職業技術學院 機電工程系，青海 海東 810799)

0 引言

由于齒輪箱故障振動信號稀疏、效果差，包含大量的噪聲，所以對齒輪箱故障診斷在于如何剔除噪聲信號和有效提取齒輪箱故障信號特征[1-3]。近年來很多學者針對齒輪箱的故障診斷開展研究。楊秀杰等人提出的匹配追蹤在齒輪故障診斷中的應用，成功提取了故障齒輪的沖擊信號[4]；王平等人發表了匹配追蹤算法的優化及其在滾動軸承故障診斷中的應用，進而對匹配追蹤算法進行優化，更好地剔除噪聲信號[5]。匹配追蹤算法每次迭代的結果是次最優的，這導致重構的信號精度不夠，需要的內存大，運行時間長，效率低[6]。基于此，王聰等人提出齒輪箱故障診斷中的自適應匹配追蹤算法[7]，該方法通過定量提取故障特征，將已知故障信號分類特征與實驗信號特征進行對比，成功提取齒輪箱故障特征，并對故障類型進行分類。SAMP算法需要多次去選擇信號的稀疏度，而稀疏度的選取直接影響算法重構信號的精度，且SAMP算法迭代過程中每次只選擇一個原子來更新子集合，這都導致重構時間過長，而且每次重構時恢復數據的計算存在誤差[8-10]。為了提高齒輪箱軸承內外圈在傳動振動過程中故障診斷能力，采用自適應匹配追蹤(SAMP)算法建立了故障診斷模型，并展開了仿真分析及實驗驗證。

1 自適應匹配追蹤算法

1.1 自適應匹配追蹤算法

本文主要采用SAMP算法提取齒輪的故障特征。SAMP算法是在自適應匹配追蹤算法基礎上加入步長和支撐集的概念[11-12]，可以在未知信號稀釋度的情況下，應用回溯思想，經過預先、候選以及剪裁三步，分段進行。在每一段都采用逐步更新步長、不斷增大支撐集、增加原子規模逐步逼近稀疏度的方法，直至達到迭代條件，退出迭代，來更加精確地重構故障信號。自適應匹配追蹤算法能夠有效降低齒輪箱振動故障信號中的噪聲，同時減少了重構的時間。對于稀疏性差的信號也能有相對好的處理效果。基本原理如圖1所示。

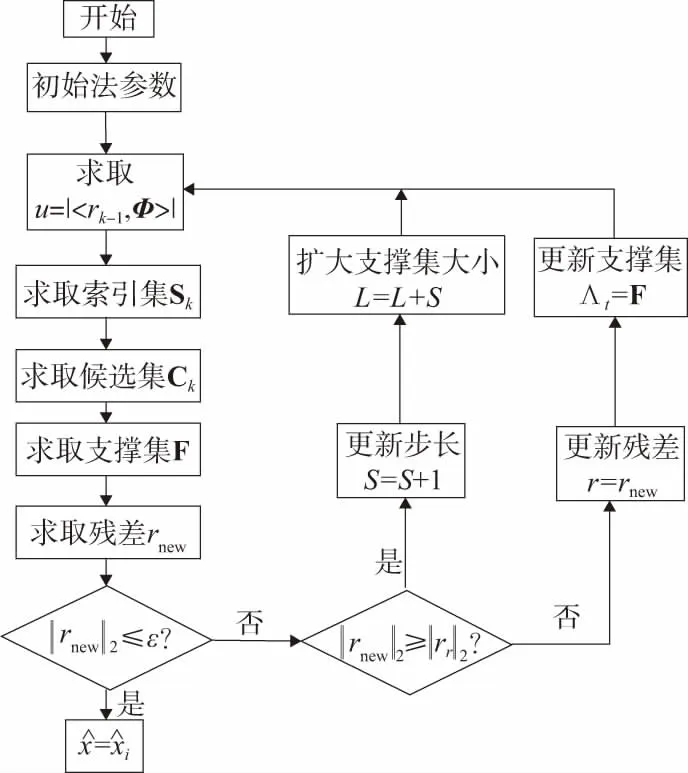
圖1 SAMP算法基本原理圖

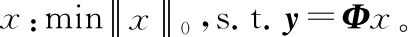
U=abs[ATrt-1] (即計算〈rt-1,aj〉，1≤j≤N)

(1)

式中：選擇u中L個最大值，將這些值對應A的列序號j構成集合Sk(列序號集合)。

SAMP算法分多階段迭代，在每個階段不改變支撐集的大小。

另At={aj}，再求取y=Atθt的最小二乘解：

(2)

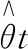
(3)

1.2 SAMP算法的有效性驗證

為了驗證SAMP算法的有效性，本文構造了一個一維隨機信號，測量個數M=64，信號長度N=256。分別通過SAMP算法作仿真信號的重構信號與殘差圖，信號稀疏度與測量精度圖。

由圖2(本刊黑白印刷，相關疑問咨詢作者)的SAMP算法重構圖可知，SAMP算法能夠精確重構出一維隨機仿真信號，能夠剔除信號的殘差信號，并提出信號的主要特征。

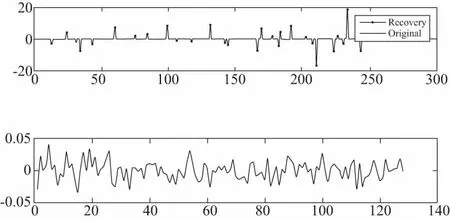
圖2 SAMP算法重構圖

由于大多數信號不具備稀疏性，需要選取合適的測量矩陣和稀疏矩陣。本文構造了一個N×N的隨機高斯測量矩陣，稀疏矩陣選擇單位矩陣，運用到SAMP算法能夠處理稀疏性差信號，且重構精度高。步長的選取也影響重構的精度，處理齒輪箱故障振動信號時，選擇固定步長為5，經過驗證能夠保證稀疏度估計的準確性。本文改變以往匹配類追蹤算法選擇設置迭代步數作為終止條件的方法，把殘差值是否達到0作為終止條件，能夠更加有效地使噪聲值降到最低，更加有效地提取故障的主要特征。

2 仿真分析

2.1 仿真軸承故障信號

在實際工作中，滾動軸承存在微弱振動，不會對正常工作產生影響，當有部分零件出現損傷時，損傷的滾動軸承的零部件會有周期性振動。振動信號的表達式如下：

(4)

式中：M為沖擊的個數；Bm為沖擊的幅值；β為沖擊的衰減系數；Tp為相鄰沖擊之間的間隔；fc為故障的特征頻率(fc=1/Tp)；fre為共振頻率。

2.2 軸承的外圈振動信號

為了驗證SAMP算法對軸承故障信號的降噪效果，簡化軸承的外圈故障信號數學模型，便于分析軸承故障。其表達式如下：

(5)

設軸承固有振動頻率為fn=1 000 Hz，位移常數為y0=5，阻尼系數為ζ=0.1，沖擊周期為0.01 s，采樣頻率為fs=4 096 Hz，采樣點數N為1 024。加入噪聲N(t)為高斯噪聲信號。轉頻fr=12，外圈通過頻率為foc=36 Hz。

如圖3所示，從SAMP算法重構軸承外圈仿真加噪信號時域波形圖中看到，軸承外圈故障仿真加噪信號被淹沒在噪聲中。對比圖2、圖3，通過SAMP算法對軸承外圈故障仿真加噪信號處理，不僅能夠看到信號呈周期性波動，還能夠清楚看到齒輪的故障。從頻譜圖中能夠清楚顯示了滾動軸承的固定頻率為1000Hz,且固定頻率周圍出現(1 000±36)Hz的邊頻帶。

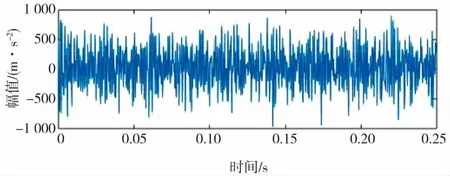
圖3 SAMP算法重構軸承外圈仿真加噪信號圖

2.3 軸承內圈振動仿真信號

簡化軸承的外圈故障信號數學模型，便于分析軸承故障。其表達式如下：

(6)

Bm=cos(2πfrt+ΦA)+y0

(7)

式(6)-式(7)中，設軸承固有振動頻率為fn=1 000 Hz，位移常數為y0=5，阻尼系數為ζ=0.1，沖擊周期為0.01 s，采樣頻率為fs=4 096 Hz，采樣點數N為1 024。加入噪聲N(t)為高斯噪聲信號。轉頻fr=12，內圈通過頻率為foc=59 Hz。

從圖4時域波形圖中看到，軸承內圈故障仿真加噪信號不呈周期性波動。經過SAMP算法處理的軸承內圈故障仿真信號呈周期性波動，能夠清楚看到滾動軸承的故障。SAMP算法重構軸承內圈仿真加噪信號頻譜圖能夠清楚顯示了滾動軸承的固定頻率為500Hz，且固定頻率周圍出現(500±20)Hz的邊頻帶。在SAMP算法重構軸承內圈仿真加噪信號譜圖中顯示了軸承內圈通過頻率60Hz以及轉頻10Hz，且出現軸承內圈通過頻率的5倍頻，在軸承內圈通過頻率周圍出現(60±10)Hz，且軸承內圈通過頻率和倍頻以及邊頻帶呈現逐步衰減，故障特征明顯。

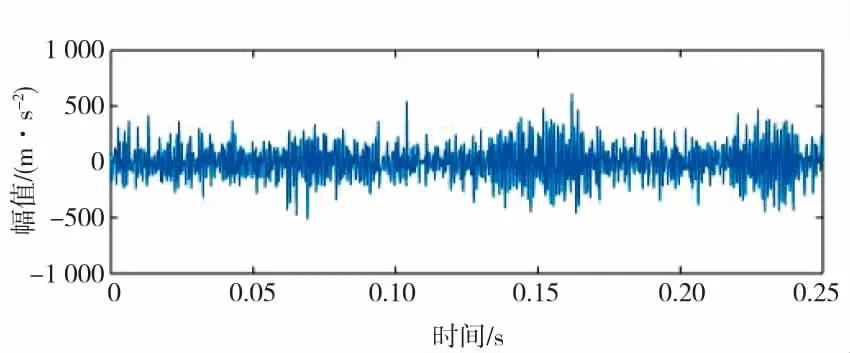
圖4 SAMP算法重構軸承內圈仿真加噪信號圖

3 結語

1)軸承外圈故障仿真信號呈周期性波動，能夠清楚看到滾動軸承外圈的故障，軸承外圈的通過頻率及其倍頻呈現逐步衰減，軸承外圈故障仿真加噪信號被淹沒在噪聲中。通過SAMP算法對軸承外圈故障仿真加噪信號處理，能夠看到信號呈周期性波動。

2)軸承內圈的通過頻率和倍頻以及邊頻帶呈現逐步衰減，故障特征明顯。從SAMP算法重構軸承內圈仿真加噪信號時域波形圖中看到，軸承內圈故障仿真加噪信號不呈周期性波動。經過SAMP算法處理的軸承內圈故障仿真信號呈周期性波動。