汽車高速公路橫坡轉向穩定性分析

李松玨，謝欣然，吳明虎，馮清，楊弘毅，魏登，楊鑫

(成都理工大學工程技術學院，四川 樂山，614000)

0 引言

轉向穩定性是汽車研究的重點，區別于常見轉向穩定性研究，本文根據特定行駛工況，建立了含軸距和輪距的汽車橫向坡道轉向行駛工況的動力學和數學模型。通過對該數學模型的仿真，可以得到所設計的軸距和輪距是否使汽車轉向穩定性變差，從而預測軸距和輪距設計是否合理。這縮短了汽車設計周期，降低汽車的設計成本，提高了設計效率。

1 橫向坡道轉向行駛汽車動力學模型的建立

要分析汽車轉向穩定性，首先要建立相應的汽車力學模型[1]。在本文中，忽略汽車懸架彈性變形和輪胎垂直路面的彈性變形，只考慮汽車輪胎的彈性側偏。現代汽車常在高速公路行駛，而高速公路為便于排水，或在轉彎處為避免轉向運動產生的離心力導致汽車側翻要設立超高，即有橫向坡度。由此建立汽車在橫向坡道轉向行駛的動力學模型，如圖1所示。

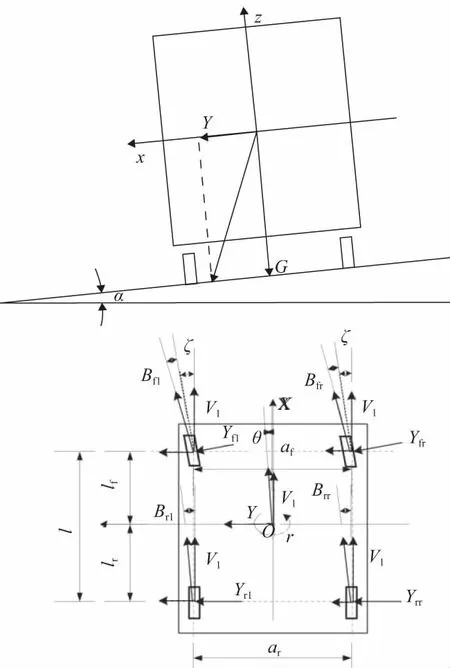
圖1 汽車橫向坡道轉向行駛動力學模型

橫向坡道坡度α根據國標《JTG-B01-2014-公路工程技術標準》中的規定，由表1確定。本文取橫向坡道坡度分別為0°、3.43°、5.71°。

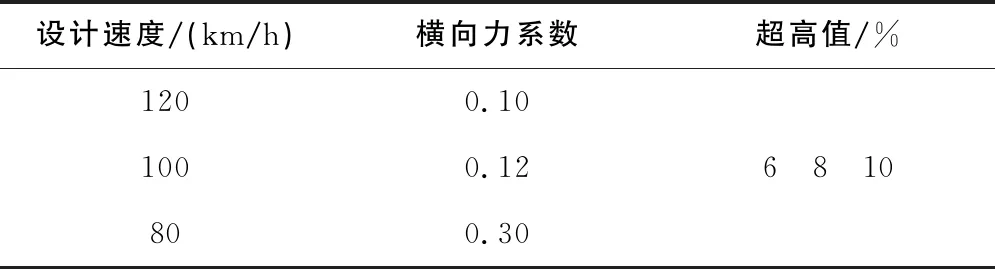
表1 橫向坡道超高值

2 根據力學模型建立數學模型

根據圖1的汽車橫向坡道轉向行駛動力學模型可以逐步分析后建立數學模型。

汽車在橫向坡道轉向行駛時，過質心的橫向截面內，重力分力為Y。

汽車車輪還受到方向為側向的側偏力的作用。4個車輪共4個側偏力，分別為：Yfl、Yfr、Yrl、Yrr。

從力學模型圖1可以看出，汽車轉向輪航向即速度方向與x軸即汽車的縱向有一個夾角ζ，該夾角是轉向輪的轉向角，同時也是汽車轉向輪速度方向與其在x軸上速度分量的夾角。

分析圖1，Yfl、Yfr、Yrl、Yrr作用于輪胎，其方向基本垂直于汽車航向，即和汽車橫向方向y軸方向基本一致。同時，汽車在橫向斜坡上行駛，汽車重力在過質心的橫向截面內的分力Y也和汽車航向基本垂直，也和汽車橫向方向y軸方向基本一致。Y構成了汽車在橫向坡道轉向行駛的對汽車轉向穩定性的側向干擾力。

汽車轉向穩定性可以分別用質心側偏角和橫擺角速度響應來評價[2]。

由上分析，建立汽車側向(橫向)運動方程如下：

(1)

Yfl、Yfr、Yrl、Yrr會產生作用在汽車上的繞坐標系z軸的橫擺力矩。據此分析，建立汽車橫擺運動方程如下：

(2)

式中Iz為汽車繞z軸的轉動慣量。

根據式(1)、式(2)，可得如下方程：

(3)

(4)

式(3)、式(4)成為描述汽車在橫向坡道上轉向行駛的數學模型。式中同時包含了參數軸距和輪距。從這兩式可以看出，轉向輪轉向輸入任意角度ζ、汽車的運動與地面坐標系的位置和汽車航向無關。汽車的軸距、輪距以及輪胎的側偏剛度、質量、高速公路的橫向坡度將會影響汽車的運動。汽車質心側偏角θ以及橫擺角速度r導致汽車產生的角度組成汽車轉向輪轉向角ζ[3]。其中，θ和r是評價汽車轉向穩定性的主要參數[4]。

3 汽車橫向坡道轉向行駛仿真

3.1 運用Matlab/simulink建立仿真模型

Matlab是一款功能強大的應用軟件。Matlab中的simulink工具箱用于仿真分析，可以獲得可視化數據用于分析，十分方便快捷。本文運用simulink工具箱構建汽車橫向坡道轉向行駛simulink仿真模型。對于類似的與橫向動力學相關的設計方法理念，近年來的研究很多。WARTH G等在Matlab/simulink中建立14自由度的非線性整車模型，通過該模型，論證了所設計的控制器的有效性[5]。RUBI-MASSEGJ等運用仿真的方法驗證了所設計的懸架靜態輸出反饋控制器性能良好[6]。JAVANSHIR I等人利用仿真軟件對越野車懸架進行建模仿真并優化懸架幾何參數，同時根據仿真結果，分析了懸架幾何參數優化前后對越野車轉向穩定性的影響[7]。AOUADJ N等設計了車輛動力學控制系統，并通過仿真證明了該控制系統的有效性和對整車轉向穩定性的提高[8]。崔勇等運用仿真軟件對整車轉向穩定性做出了分析[9]。

3.2 仿真分析數據和轉向輪轉向角階躍輸入

simulink建模仿真所需數據為某車型數據，如表2所示。

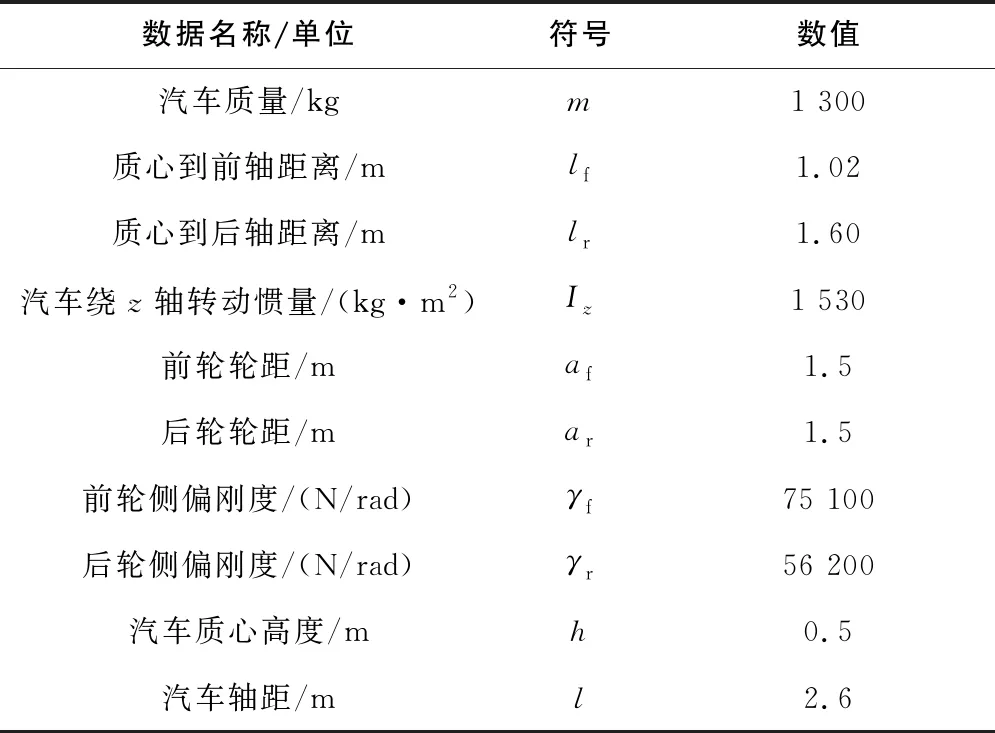
表2 仿真所需數據

本文根據表2的數據，通過對所建的simulink模型的仿真，分析該型汽車在道路不同橫向坡度和不同車速兩方面的轉向穩定性，從而分析該車型的軸距和輪距對轉向穩定性的影響，最后得出該車型的軸距和輪距設計是否滿足汽車轉向穩定性的結論。

仿真輸入采用轉向盤的角階躍輸入。角階躍輸入試驗是路上試驗中最典型的試驗[10]。汽車對轉向盤輸入的瞬態響應能夠通過階躍試驗反映[11]。本文中，轉向盤的角階躍為轉向輪的轉向角階躍輸入。

3.3 轉向輪角階躍輸入final值為定值的仿真結果

轉向輪轉向角階躍輸入時間為10s，同時也是仿真時間。

轉向輪轉向角階躍輸入按如下工況：由于汽車的轉向盤存在自由行程，因此，轉向輪的轉向角階躍輸入initial值在0.5 s前為0。0.5 s的時間意味著轉向盤轉過自由行程。階躍輸入的final值為0.01 rad。

汽車橫向坡道轉向行駛工況如下：該型汽車在橫向坡度為0°、3.43°、5.71°的橫向坡道，分別以速度為80km/h、100km/h、120km/h速度轉向行駛。階躍輸入仿真結果如圖2所示；橫擺角速度、質心側偏角、側向加速度仿真結果如圖3所示。

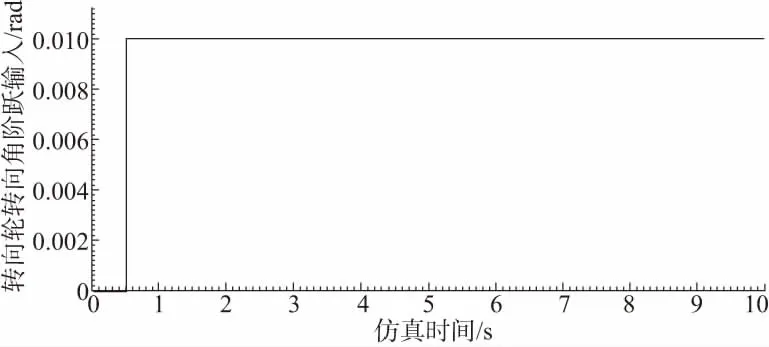
圖2 階躍輸入曲線

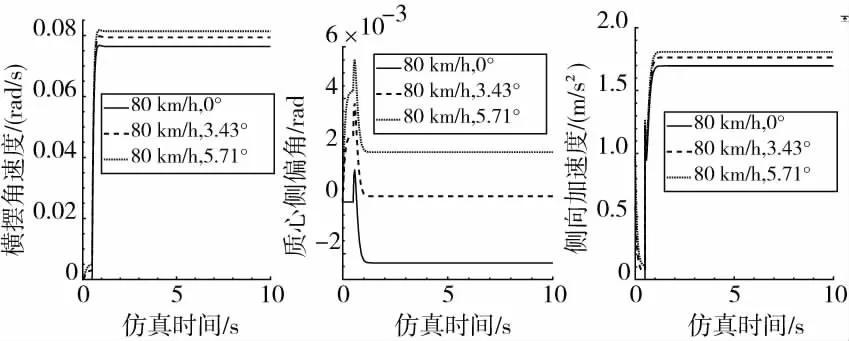
圖3 橫擺角速度、質心側偏角、側向加速度響應曲線

4 仿真結果分析

根據圖3的仿真結果，該型汽車分別在橫向坡度為0°、3.43°、5.71°的橫向坡道，階躍輸入final值為0.01rad時，分別以速度為80km/h、100km/h、120km/h速度轉向行駛，側向加速度峰值和穩定值均小于該車在相應橫向坡度的側翻閾值，這意味著該型汽車在此階躍輸入下不會發生側翻。

圖3中該型汽車在不同坡度以不同速度轉向行駛時，橫擺角速度超調量最大為103.27%，最小為100.5%。超調量較小且變化不大，該型汽車能夠迅速從橫擺角速度峰值回到穩定狀態，說明該型汽車轉向穩定較好。橫擺角速度、側向加速度各自的峰值響應時間能夠反映汽車對轉向響應的靈敏程度[12]。質心側偏角和側向加速度峰值時間較小，說明該型汽車瞬態響應迅速，轉向靈敏。

根據本文表2數據，計算出lfγf-lrγr<0。即該型汽車有不足轉向特性。該型汽車特征速度vch=50km/h。當速度為80km/h、100km/h、120km/h時，均大于特征速度vch。故該型汽車質心側偏角穩態值在同一橫向坡度上隨速度的增加而減小,直至為負值。在速度120°、橫向坡度為5.71°時，質心側偏角達到-0.006762rad。當該型汽車以同一速度在不同坡度上轉向行駛時，不同橫向坡度導致的側向力Y大小隨橫向坡度不同而不同，橫向坡度為5.71°時，Y最大。所以當該型汽車以同一速度在不同橫向坡度的橫坡上行駛時，Y與車輪的側偏力共同平衡離心力，質心側偏角隨橫向坡度的增加而減小。在橫向坡度為5.71°時，質心側偏角最小。說明該車型在橫向坡道行駛時轉向穩定性較好。汽車的側向力越大，汽車抵抗干擾的能力越強,側向偏移越小[13]。

5 結語

本文建立了考慮某車型橫向坡道轉向行駛的動力力學模型，并建立了相應的數學模型。根據此數學模型建立了仿真模型。仿真結果為該車型以80km/h、100km/h、120km/h的速度，在不同橫向坡度轉向行駛時的橫擺角速度、質心側偏角、側向加速度的數據視圖。根據這些數據視圖分析了該車型在橫向坡道上轉向行駛的轉向穩定性。

分析結果說明該型汽車軸距、輪距設計符合汽車轉向穩定性。