基于Deform-3D軸向振動鉆削P20有限元仿真

張衛鋒，張燦祥，劉致君，吳志強

(青島科技大學 機電工程學院，山東 青島 266061)

0 引言

在模具行業中，P20模具鋼憑借其硬度均勻、良好的拋光和光蝕刻花以及其物理特性組織致密等性能，廣泛應用于熱塑性塑膠注塑模具上。而模具常用的連接方法是用螺絲緊固和銷釘定位，因此，需要大量的連接孔。傳統的鉆削加工有軸向力大、表面質量差、刀具磨損嚴重等問題。

為解決以上問題，在20世紀五六十年代日本限部淳一郎教授最早提出在刀具上加入振動的理論，并進行了試驗驗證，另外，他還提出了在傳統的機加工方式中加上振動，有利于改善加工工藝性；在國內，華中理工大學熊烽等人研制了使用動態采集的方法分析軸向力和轉矩；吉林工業大學王立平等人通過理論分析了低頻振動可以消除出口毛刺的作用，并對比了普通鉆削，另外，分析了低頻振動鉆削中鉆頭壽命和橫向偏移機理，得出振動鉆削定位精度較高，偏移被消除[1-4]。

本文采用Deform-3D有限元分析軟件研究在鉆削P20模具鋼的過程中，鉆削參數對軸向力和轉矩的影響規律。

1 軸向振動鉆削有限元模型

對于Deform-3D有限元分析軟件來說[5-6]，其結構是由前處理器、模擬處理器、后處理器3大模塊組成。具體的分析步驟如圖1所示。

圖1 Deform-3D仿真分析步驟圖

本文中將涉及到大量的仿真試驗，其有限元模型的建立過程基本類似，所以，本節將通過試驗設計其中的某一組參數，詳細地敘述軸向振動鉆削有限元模型的建立過程：以φ5mm的兩刃麻花鉆、工件直徑φ10mm、厚度1.5mm、進給速度0.15mm/r、旋轉速度1200r/min、振幅20μm、頻率100Hz為示例，建立有限元模型。

1.1 工件及麻花鉆模型建立與網格劃分

在Deform-3D工具模塊中，創建麻花鉆實體模型，選擇的鉆頭直徑為φ5mm的兩刃麻花鉆，定義鉆頭為剛性體即可。另外，工件模型直接輸入直徑φ10mm、厚度1.5mm即可生成模型，定義工件為塑性體。在網格劃分設置中[7-8]，工件網格的劃分采用絕對網格劃分類型，最大網格尺寸和最小網格尺寸的比例設為6，最小單元邊長為0.05。麻花鉆網格的劃分采用相對網格劃分類型，定義刀具20000個元素的網格，最大網格尺寸和最小網格尺寸的比例設為4。如圖2所示。

圖2 麻花鉆模型圖

1.2 材料定義

定義麻花鉆材料為WC(硬質合金)，不添加鍍層。對于工件材料來說，在鉆削過程中大應變、高應變率和高溫升的情況是經常發生的[9-10]。因此，通常使用的材料本構關系為J-C模型，其函數關系如式(1)所示，特征參數如表1所示。

表1 P20的J-C特征參數

(1)

1.3 工件接觸以及摩擦定義

首先，固定工件側面所有節點的速度，并為所有表面分配熱交換邊界條件，工件處于完全固定的狀態。此外，在接觸設置中，建立鉆頭與工件的接觸關系：鉆頭自動定義為主要對象，工件自動定義為從屬對象，摩擦類型為剪切摩擦，摩擦系數選用恒定摩擦，輸入0.6即可；另外，在鉆削過程中，切屑可能會接觸到工件，所以要創建一個工件與工件之間的自接觸。

1.4 工具運動及其他參數設置

在軸向振動鉆削中，通過對刀具施加參數配置，以此來實現轉動、進給以及振動的運動。在工具運動設置選項內，設置工具沿著z的負方向進給，并繞z軸旋轉，角速度必須以弧度/秒為單位定義。

振動鉆削的速度是一個周期性的函數[7]，即由位移-時間函數式(2)進行求導，得出速度-時間的關系為式(3)。

Z=frNT+Asin(2πfT)

(2)

v=frN+2πfAcos(2πfT)

(3)

本次仿真的參數采用：fr=0.15mm/r；N=1200r/min(即N=20r/s)；f=100Hz；A=20μm，代入式(4)得

v=3+12.56cos(200πT)

(4)

由式(4)可知，該振動函數的振動周期為0.01s。對于整個振動鉆削過程來說，勢必要精確得出工具各個時間點的速度。因此，利用MATLAB軟件將時間T定義為T=0∶0.001∶20。然后，進入Deform-3D軟件，將MATLAB得出的數據導入其中，就完成了軸向振動鉆削工具的進給速度，如圖3所示。

圖3 軸向振動鉆削工具實時進給速度圖

另外，將環境溫度、工件和刀具溫度統一設定為20℃，熱傳導系數為45N sec-1·mm-1·℃-1，熱對流系數0.02N sec-1·mm-1·℃-1(即為使用空氣冷卻劑)；刀具的磨損模型選擇適合于金屬切屑的usui模型[10]：

(5)

式中：ω為磨損體積；T為絕對溫度；p為壓力；V為相對速度；a、b為試驗系數，分別取1×10-5和855。

1.5 模擬設定

設置步長為0.001，總模擬步數50000步，每隔25步保存一組數據。另外，設置鉆頭停止距離為2mm，即為將工件鉆透。以上兩個條件滿足其一仿真即停止[11]。

2 單因素試驗設計與分析

2.1 主軸轉速對軸向力和轉矩的影響

選擇相同的進給速度和振幅，并保持其他條件不變，研究主軸轉速對軸向力和轉矩的影響，設計試驗主軸轉速從800r/min～1200r/min，試驗參數如表2所示。

表2 主軸轉速試驗參數設計

通過3組不同轉速下得到的軸向力和轉矩的變化趨勢，給出一組代表性曲線如圖4所示。可以看出，軸向力和轉矩隨著參與切削的鉆頭長度不斷增大而從0開始慢慢增大；當鉆頭的切削刃全部參與切削后，軸向力和轉矩到達最大值。而后切削刃保持不變，軸向力和轉矩保持穩定，到達穩定切削狀態；最后，鉆頭逐漸鉆出工件，軸向力逐漸降低到0，轉矩達到穩定值。但是從曲線中可以看出，在某個時刻軸向力和轉矩會出現驟變，這是由于切屑的斷裂或者是工件網格產生了畸變，軟件進行網格重劃分所致[10,12-13]。

圖4 試驗1軸向力和轉矩的變化趨勢

表3為不同轉速下軸向力和轉矩的試驗結果。根據表3繪制出主軸轉速對軸向力和轉矩的影響趨勢，如圖5所示。可以看出主軸轉速對軸向力和轉矩的影響整體上來說并不是很大，只是有微微變化。在對P20模具鋼振動鉆削過程中，隨著主軸轉速的提高，工具外側振動的速度分量在總合成速度中作用減小，速度的動態切削角度的波動減小，導致振動鉆削對軸向力的減小作用有所減弱。因此，隨著主軸轉速的提高，軸向力有所增大；而對于轉矩來說，軸向力增大，切向力減小，轉矩即為切向力與外側切削刃到回轉中心的距離的乘積[14-15]，故隨著主軸轉速的提高，轉矩有所減小。

表3 不同轉速下軸向力和轉矩的試驗結果

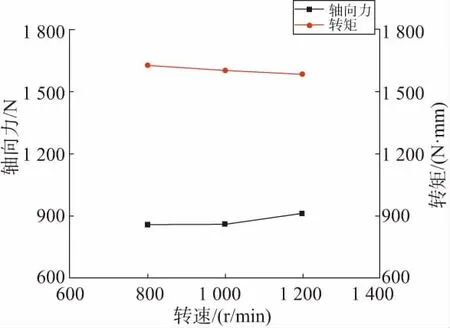
圖5 不同轉速對軸向力和轉矩的影響趨勢

2.2 進給速度對軸向力和轉矩的影響

選擇相同的主軸轉速和振幅，并保持其他條件不變，研究進給速度對軸向力和轉矩的影響。設計試驗進給速度從0.1mm/r～0.2mm/r，試驗參數如表4所示。

表4 進給速度試驗參數設計

通過3組不同進給下得到軸向力和轉矩的變化趨勢，給出一組代表性曲線如圖6所示。其曲線的分析同上。表5為不同進給下軸向力和轉矩的試驗結果，根據表5繪制出進給速度對軸向力和轉矩的影響趨勢，如圖7所示。從圖中可以明顯看出進給速度對軸向力和轉矩的影響非常大，在對P20模具鋼振動鉆削過程中，隨著進給速度的提高，工具與工件的實際切削面積增大，材料去除率響應增大，刀具每轉去除材料所做的功隨之增加，進而增大了工具所受軸向力和轉矩。

圖6 試驗2軸向力和轉矩的變化趨勢

圖7 不同進給對軸向力和轉矩的影響趨勢

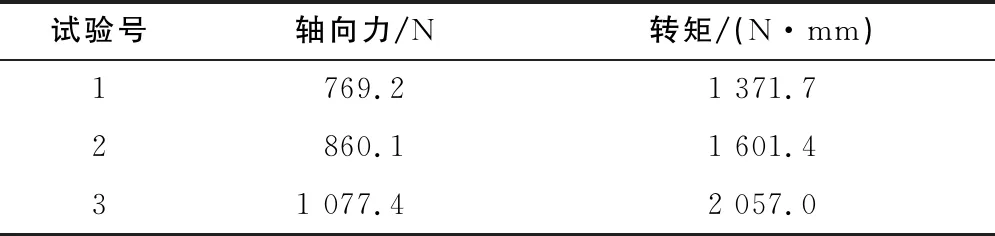
表5 不同進給下軸向力和轉矩的試驗結果

2.3 振幅對軸向力和轉矩的影響

選擇相同的主軸轉速和進給，并保持其他條件不變，研究振幅對軸向力和轉矩的影響。設計試驗振幅從10μm～30μm，試驗參數如表6所示。

表6 振幅試驗參數設計

通過3組不同振幅下得到的軸向力和轉矩的變化趨勢，給出一組代表性曲線如圖8所示，其曲線的分析同上。表7為不同振幅下軸向力和轉矩的試驗結果，根據表7繪制出振幅對軸向力和轉矩的影響趨勢，如圖9所示。隨著振幅的增大，工具所受的軸向力和轉矩都呈現降低的趨勢，這是由于振幅的提高使得材料塑性變形的抗力減小，進而使得軸向力和轉矩同時減小。

圖8 試驗3軸向力和轉矩的變化趨勢

圖9 不同振幅對軸向力和轉矩的影響趨勢

表7 不同振幅下軸向力和轉矩的試驗結果

2.4 與普通鉆削的對比試驗

選擇相同的主軸轉速和進給，并保持其他條件不變，對比普通鉆削與振動鉆削，設計試驗參數如表8所示。

表8 普通鉆削與振動鉆削的對比試驗參數設計

圖10為仿真所得的分別用振動鉆削和普通鉆削兩種不同加工方式下鉆削P20模具鋼的軸向力和轉矩的變化曲線，通過觀察圖10的曲線變化，可以看出由于普通鉆削是工具與工件之間連續接觸、擠壓以及切削，使得軸向力和轉矩的變化曲線是連續的；而振動鉆削得到的軸向力和轉矩曲線是以周期性變化的。這是因為工具與工件的周期性分離，由原始的連續切削變成了沖擊接觸，其鉆削條件得到改善。關于曲線的其他分析同上，在此不作過多描述。

圖10 不同加工方式下軸向力和轉矩的變化趨勢

表9為不同加工方式下軸向力和轉矩的試驗結果，根據表9繪制不同加工方式對軸向力和轉矩的影響趨勢，如圖11所示。從圖中可以明顯看出，相對于普通鉆削加工，軸向振動鉆削的軸向力和轉矩均有所下降。圖14中普通鉆削P20的平均軸向力和轉矩分別為962.0N、1 661.2N·mm，而在頻率為100Hz的軸向振動鉆削P20的平均軸向力和轉矩分別為860.1N、1 601.4N·mm。因此，與普通鉆削相比，在低頻的軸向振動鉆削中，已經使得平均軸向力和轉矩分別下降了11%和4%。所以，相較于普通鉆削加工來說，軸向振動鉆削可有效減小軸向力和轉矩，進而提高材料去除率。

表9 不同加工方式下軸向力和轉矩的試驗結果

圖11 不同加工方式下軸向力和轉矩的影響趨勢

3 正交試驗設計與分析

3.1 試驗設計

在軸向振動鉆削過程中，合理地選擇鉆削參數對提高加工質量和效率將起到很大的作用。因此本小節采用正交試驗法仿真研究主軸轉速、進給和振幅對軸向力以及轉矩的影響，以此來驗證單因素試驗的結論，并通過計算極差值找出影響最大的因素。表10為正交試驗的因素水平表，表中因素數為3，水平數為3，屬于等水平正交表，選擇最接近的正交表為L9(34)，建立表11正交試驗的安排。

表10 因素水平表

表11 正交試驗因素安排

3.2 試驗結果及分析

通過9組正交試驗得出的軸向力和轉矩的整體變化趨勢，現給出3組代表性曲線如圖12所示，整理其數據得出平均軸向力和轉矩的正交試驗結果，如表12所示，對其結果進行極差計算，得出表13。其中，進給速度的極差值最大，說明在軸向振動鉆削P20過程中，進給速度是影響軸向力和轉矩最主要的因素。各影響因素的影響程度的排序依次為：進給速度>振幅>主軸轉速。

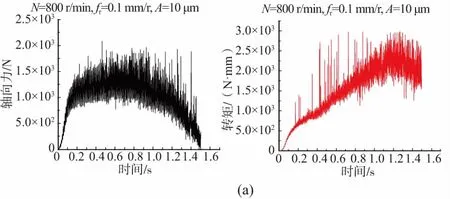
圖12 不同鉆削參數下部分試驗軸向力和轉矩的變化趨勢

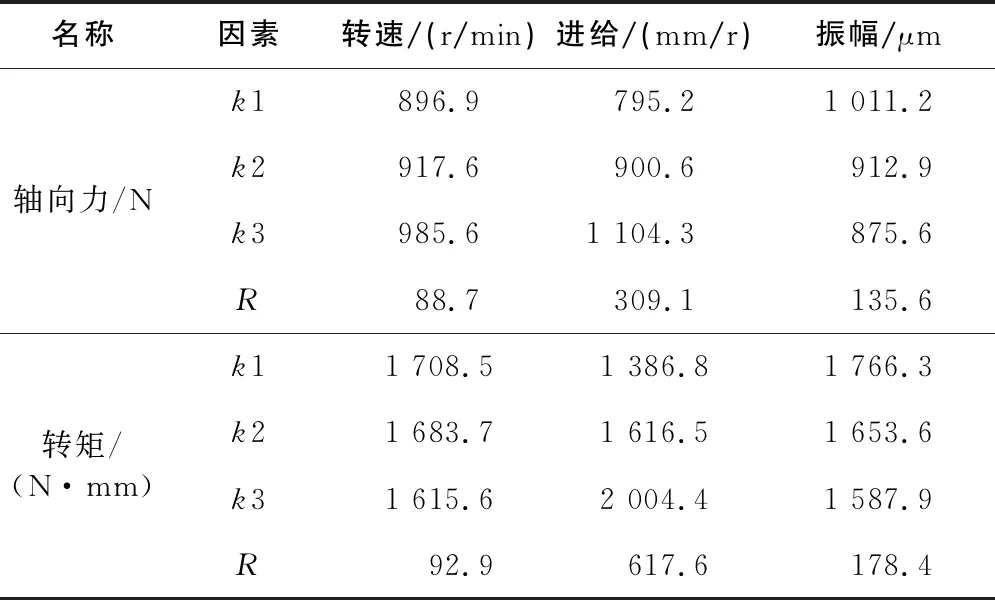
表12 正交試驗極差分析

表13 正交試驗結果

根據極差分析表的均值k，繪制出各因素水平趨勢圖，如圖13所示。主軸轉速提高，軸向力呈現緩慢上升的趨勢，而轉矩呈現緩慢下降的趨勢；進給速度提高，軸向力和轉矩都呈現急劇上升的趨勢；而隨著振幅的提高，軸向力和轉矩均呈現下降的趨勢。其規律與單因素試驗規律相同。

圖13 振動鉆削P20軸向力和轉矩因素水平趨勢圖

4 結語

文章基于Deform-3D軟件對P20進行振動鉆削仿真模擬，通過研究鉆削參數對于鉆頭軸向力和轉矩的影響，得出如下結論：

1)通過單因素和正交試驗兩種試驗方法研究得出軸向力隨著主軸轉速的增加有微微增大的趨勢，轉矩有微微減小的趨勢；隨著進給速度的增大而增大，而軸向力和轉矩隨著振幅的增大而減小。通過極差值大小可以看出，各影響因素的影響程度的排序依次為：進給速度>振幅>主軸轉速。

2)相對于普通鉆削加工來說，軸向振動鉆削的軸向力和轉矩均有所下降。