行星滾柱絲杠運動原理及有限元分析

王家健，張慶

(南京理工大學 機械工程學院，江蘇 南京210094)

0 引言

標準式行星滾柱絲杠(下面簡稱行星滾柱絲杠)是將螺旋運動和行星運動結合在一起，將絲杠旋轉運動轉變為螺母直線運動的傳動機構，具有承載能力強、剛度大、精度高、耐磨損、耐沖擊和壽命長等特點，廣泛應用于工業和國防軍工領域[1]。

國內對行星滾柱絲杠的理論研究已經有一定的基礎。靳謙忠和馬尚君通過對行星滾柱絲杠的運動原理分析給出了相關參數的匹配設計條件[2-3]。在螺紋接觸分析方面，許多學者基于赫茲接觸理論和有限元方法進行研究，分析了螺距、牙型角、滾柱個數、載荷等因素對接觸應力的影響，為提高行星滾柱絲杠的承載能力提供了參考[4-6]。但是目前對行星滾柱絲杠的有限元接觸分析，都是將絲杠與滾柱、滾柱與螺母分開分析，而且只是分析一組或者幾組螺紋接觸對，沒有對整體結構進行有限元分析。

1 行星滾柱絲杠運動原理分析

行星滾柱絲杠主要由絲杠、滾柱、螺母、內齒圈、保持架和彈性擋圈組成，結構形式如圖1所示。

圖1 行星滾柱絲杠結構形式

行星滾柱絲杠在工作時，絲杠通常作為動力輸入端，只繞自身軸線轉動；螺母通常與負載連接，只沿自身軸線移動；滾柱在螺母和絲杠之間做行星運動，并且與螺母相對軸向位移為零，與螺母一起沿軸向移動。行星滾柱絲杠運動簡圖如圖2所示。

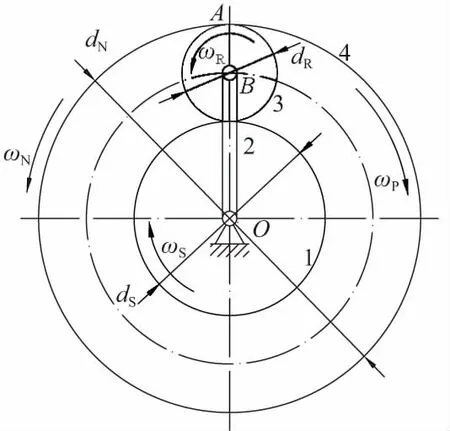
1—絲杠；2—保持架；3—滾柱；4—螺母。

圖2中：dS、dR和dN分別為絲杠、滾柱和螺母的螺紋中徑，由圖1中幾何關系有dN=dS+2dR；ωS、ωN、ωR和ωP為絲杠、螺母、滾柱和保持架的旋轉角速度，ωN通常為0；pS、pR和pN分別為絲杠、滾柱和螺母的螺紋螺距；nS、nR和nN分別為絲杠、滾柱和螺母的螺紋頭數，nR通常取1。

1.1 角速度分析

參照行星齒輪傳動的分析方式[7]，給整體一個公共角速度，大小等于ωP，方向與保持架旋轉方向相反，各構件的角速度變化如表1所示。

表1 角速度變化對比

根據表1，由傳動比關系可得：

(1)

(2)

由式(1)、式(2)及dN=dS+2dR可得：

(3)

(4)

以上是假設滾柱與絲杠之間為無滑動的滾動，實際上滾柱與絲杠嚙合可能存在滑動，所以ωR和ωP的實際數值要比理論值偏小。

1.2 螺紋旋向和頭數分析

通常螺紋嚙合需要保證螺距相等，即pS=pR=pN=p。螺旋副在旋轉嚙合過程中螺旋曲面的變化可以等效為其沿軸線的平移，移動方向可以通過左右手法則判斷[8]。

1)滾柱和螺母螺紋旋向和頭數分析

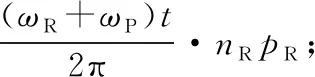
(5)

因為滾柱與螺母相對位移必須為0，所以式(5)中應取“-”，即滾柱與螺母螺紋旋向相同。由式(3)、式(4)、式(5)及LRN=0可得

nN=dS/dR+2

(6)

2)滾柱和絲杠螺紋旋向和頭數分析

與滾柱和螺母的相對位移分析方法相同，滾柱和絲杠的相對位移LRS可以表示為

(7)

其中“+”號表示絲杠與滾柱旋向相同，“-”號表示絲杠與滾柱旋向相反。由式(3)、式(4)、式(7)可得

(8)

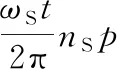
nS=dS/dR+2

(9)

滾柱和螺母相對絲杠的位移可以表示成

(10)

1.3 滾柱齒輪與內齒圈傳動分析

1)因為齒輪傳動為非承載部分，所以通常采用直齒圓柱齒輪嚙合。設滾柱端齒輪和內齒圈齒數分別為zR和zN，模數為m。齒圈與螺母固連在一起，要滿足滾柱與螺母純滾動，則齒輪傳動比與螺紋傳動比相等，即

zN/zR=dN/dR

(11)

2)因為滾柱端齒與絲杠也要嚙合，為了防止齒頂圓與絲杠螺紋牙底干涉，滾柱端齒齒頂圓直徑不能大于滾柱螺紋大徑dRa[2]，即

(12)

3)齒輪嚙合傳動必須要滿足最小齒數要求，避免根切，即

(13)

當調整齒數和模數無法滿足最小齒數要求時，可以采用變位齒輪設計或者改用短齒制，必要時可以采用非標準壓力角齒輪設計[2]。

2 行星滾柱絲杠有限元建模

根據技術指標要求，結合上一節中運動分析結果，進行行星滾柱絲杠的結構設計；然后建立行星滾柱絲杠的三維建模；再把模型導入到ANSYS Workbench軟件中，進行有限元建模[9]。

行星滾柱絲杠主要螺紋零件的主要參數如表2所示，齒輪零件的主要參數如表3所示。

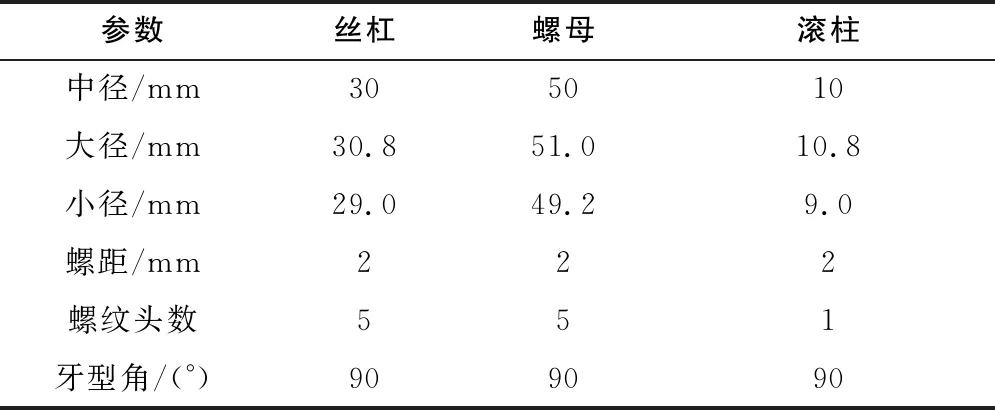
表2 螺紋零件參數

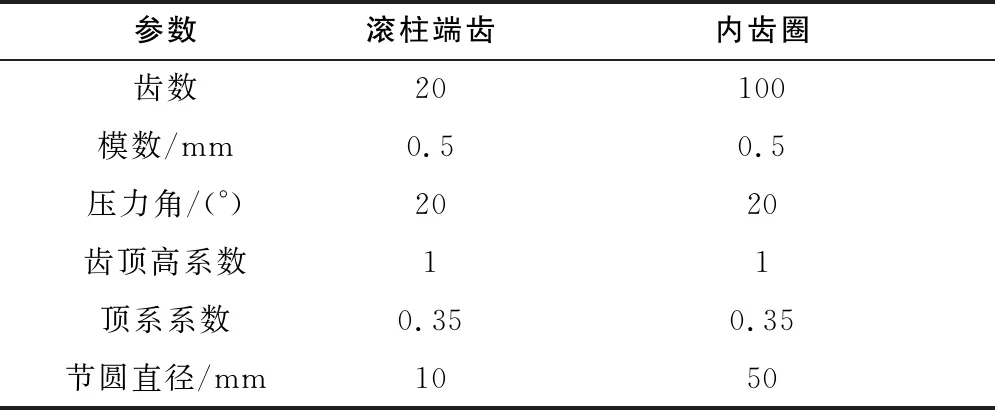
表3 齒輪零件參數

2.1 三維模型簡化

對模型進行簡化，去除擋圈等零件以及零件的倒角和孔等特征，絲杠只截取嚙合部分；行星滾柱絲杠為對稱結構，滾柱個數為10且均勻布置，所以取模型的1/10進行研究。螺母上承受的軸向載荷為150kN，所以簡化后的模型承受的軸向載荷為15kN；將簡化后的三維模型導入到ANSYS Workbench中，如圖3所示。

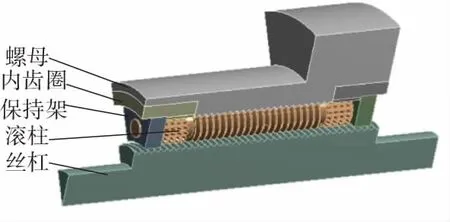
圖3 有限元簡化模型

2.2 材料分配及網格劃分

對導入的模型進行材料分配，材料選用淬硬的軸承鋼GCr15，其耐磨性好、硬度高，適合行星滾柱絲杠高承載、高剛度的要求。彈性模量E=200GPa，泊松比ν=0.3，屈服極限σS=1 667～1 814MPa。材料分配后對模型進行網格劃分，如圖4所示。

圖4 有限元網格模型

2.3 接觸設置

絲杠螺紋與滾柱螺紋、滾柱螺紋與螺母螺紋、滾柱端齒與內齒圈，這3處接觸采用Frictional接觸類型，可以法向分離和切向滑動。當切向分力大于最大靜摩擦力時發生切向滑移，這樣更符合行星滾柱絲杠的實際運動情況。

內齒圈與螺母之間為Bonded接觸類型，法向和切向均無相對位移。

保持架只對滾柱起導向作用，不是承載及定位的零件，所以滾柱與保持架、保持架與內齒圈之間為Frictionless接觸類型，法向和徑向都可以有小位移。

2.4 邊界條件設置

螺母只沿自身軸向平移，采用Displacement約束，只保留軸向移動自由度；對螺母法蘭面施加15kN的軸向載荷。

滾柱即做行星運動又沿軸線平移，采用Cylindrical Support約束，保留旋轉和軸向平移自由度。保持架同樣既有旋轉運動又有軸向移動，也采用Cylindrical Support約束，保留旋轉和軸向平移自由度。

絲杠一端固定一端支承，所以固定端采用Fixed Support約束，完全限制6個自由度，支撐端采用Displacement約束，只保留軸向移動自由度。

因為模型只有1/10，所以對絲杠、保持架、內齒圈和螺母的剖面施加Frictionless Support約束，即法向無變形，其他方向可以自由變形。

3 行星滾柱絲杠有限元求解結果分析

3.1 有限元求解結果

圖5和圖6分別給出了螺母和滾柱螺紋接觸點以及絲杠和滾柱接觸點的等效應力云圖。從圖5中可以看出，螺母和滾柱螺紋接觸點最大應力在滾柱螺紋牙上，為1 499.5MPa；從圖6中可以看出，絲杠和滾柱螺紋接觸點最大應力在絲杠螺紋牙上，為1 491.4MPa。

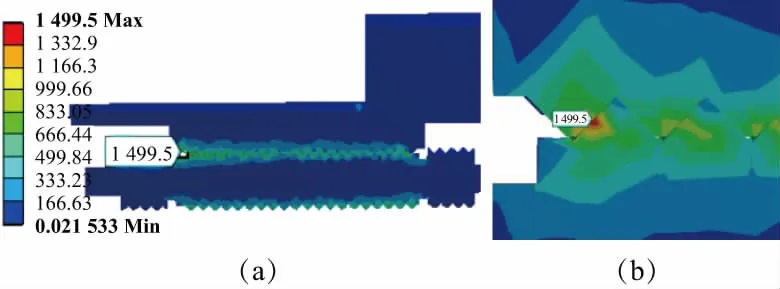
圖5 絲杠與滾柱接觸點等效應力云圖

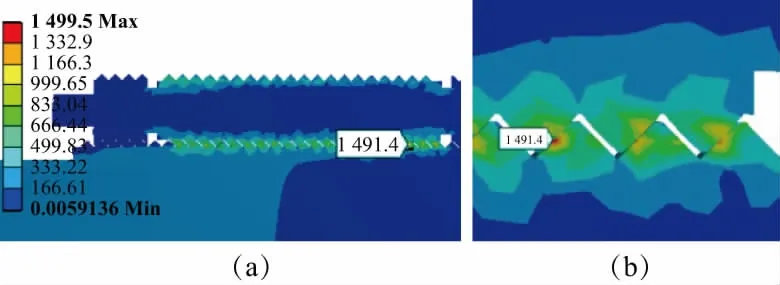
圖6 螺母與滾柱接觸點等效應力云圖

絲杠、滾柱和螺母螺紋的接觸應力都小于屈服極限，滿足強度要求。但是螺紋牙存在載荷分布不均的情況，如圖7所示，螺母左端第一個螺紋牙的等效應力最大，然后往右呈現減小的趨勢。滾柱和絲杠螺紋牙的應力情況與螺母類似。

圖7 螺母螺紋等效應力云圖

3.2 牙型角對接觸應力的影響

為了研究牙型角對螺紋接觸應力的影響，不改變螺紋的其他參數，在螺距為2mm時，分別對牙型角為60°、70°、80°、90°、100°時進行有限元仿真求解，有限元求解結果如表4所示。

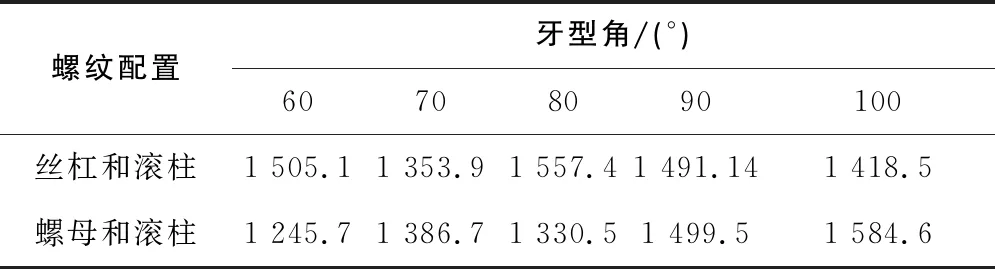
表4 不同牙型角的螺紋最大接觸應力對比 單位：MPa

從表4可以看出牙型角在70°時螺紋接觸應力最小，其次是90°，而在60°、80°和100°時，最大接觸應力都超過了1 500MPa。根據文獻[10]，牙型角與行星滾柱絲杠的傳動效率有著緊密的聯系，牙型角越大傳動效率越高，所以綜合考慮傳動效率和螺紋接觸強度，通常選擇牙型角為90°。

3.3 螺距對螺紋接觸應力的影響

為了研究螺距對螺紋接觸應力的影響，不改變螺紋的其他參數，在牙型角為90°時，分別對螺距p為1.5mm、2mm、2.5mm、3mm和3.5mm時進行有限元仿真求解，有限元求解結果如表5所示。

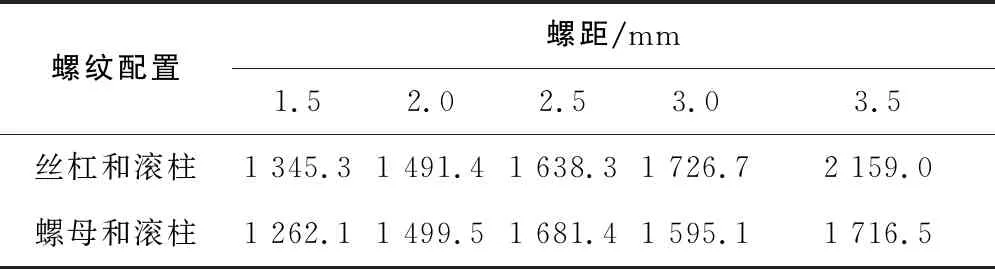
表5 不同螺距的螺紋接觸應力對比 單位：MPa

從表5可以看出，隨著螺距的增大，接觸應力變化較大，而且接觸應力有增大的趨勢。因為螺紋總長度相同，當螺距越大時，相應的螺紋接觸點越少，從而降低了行星滾柱絲杠的承載能力。

4 結語

1)通過類比行星齒輪傳動的分析方法，對行星滾柱絲杠的運動原理分析，得出絲杠、滾柱和螺母的螺紋旋向相同，螺紋頭數滿足nS=nN=dS/dR+2。

2)對行星滾柱絲杠螺紋的接觸應力進行有限元仿真分析，并且研究了螺紋的牙型角和螺距對接觸應力的影響，牙型角通常選擇90°，螺紋最大接觸應力隨螺距的增大而增大。