基于線性矩陣不等式的巡檢機器人路徑規劃

戴昊，崔志文，袁鵬，歐旋

(深圳供電局有限公司，廣東 深圳 518000)

0 引言

巡檢機器人是一種能夠完成輸電線路巡檢、應急監測、環境監測和反恐處突等任務的機器人。圖1是某公司的巡檢機器人E100。E100面向電力、市政、通信和石化等行業，為智能運維系統提供環境和工業設備狀態的監測數據。

圖1 E100巡檢機器人

巡檢機器人在任務空間運動時，首先要解決的就是路徑獲取以及路徑規劃問題。路徑規劃依賴于機器人和目標點的位置信息，通過有效的算法，求得一條連接出發點和目標點的最優軌跡；同時需要滿足諸多約束，如障礙物規避、路程和時間要求等。針對機器人的軌跡規劃，國內外學者提出了大量方法[1-5]。主要的路徑規劃有四類，第一類是基于地圖構建的路徑規劃方法，KUWATA Y等[6]將可視圖法從二維擴展到三維，并應用到無人機的航跡規劃中，但該方法沒有充分考慮路徑中的約束；肖秦琨等[7]對軌跡規劃中的Voronoi圖法進行了改進，提高了機器人運行的安全度，但不是最優解；HRABAR S E[8]使用概率圖法，在搜索空間內按照概率分布產生隨機路徑點，連接路徑點構成完整的路徑，并在三維空間內的軌跡規劃進行了仿真研究，但該路徑不一定是最優的。第二類是在基于虛擬勢場法軌跡規劃方面，侯翔[9]在人工勢場的基礎上，通過引入指數因子構造斥力函數來平衡障礙物斥力，解決了障礙物附件目標不可達問題，但容易陷入局部最小點；貝前程等[10]對傳統人工勢場進行了改進，提出改進的斥力函數方法，確保機器人能夠順利到達目標點；LIU C A等[11]將流體力學理論應用到機器人路徑規劃中，建立流場，可以獲得光滑的路徑，但對規劃中的約束考慮不足。第三類是一些學者將數學最優化的方法應用到軌跡規劃中，DOGAN A[12]在障礙物威脅概率密度函數的基礎上，提出了使用迭代步方法進行路徑規劃，并推廣到三維規劃中，規劃得到的路徑安全性較高，但未必是最優解；張劍等[13]用支持向量機對電力巡線無人機工作區域進行非線性分割，并從分割平面中選擇適當的路徑，避障性能較好。第四類是基于生物智能的方法，這種方法具有較強的搜索能力，適合搜索最優軌跡，袁佳泉等[14]在蟻群算法的基礎上，結合模擬退火算法來進行機器人的軌跡規劃，提高了計算速度；張丹紅等[15]將A*算法與蟻群算法相結合，應用到巡邏艇的路徑規劃中，求解全局最短巡邏路徑。這些方法在路徑光滑性、環境適應性和實時性上都各有優勢與局限。

本文針對巡檢機器人的任務特點，在主要的軌跡規劃方法的基礎上，提出一種結合單元分解和線性代數的航跡規劃方法。首先，描述基于Delaunay剖分法的任務環境三角劃分；然后，在此基礎上，對軌跡規劃進行數學描述，定義變量以及約束條件，將規劃問題轉化為基于線性矩陣不等式的最優化問題；最后，結合實際的任務環境，對環境進行簡化，并利用簡化后的模型進行仿真計算以驗證本文方法的正確性。

1 任務環境三角劃分

定義二維三角剖分：二維實數域上的點集V，以此點集中的點作為端點，構成封閉線段e，E為線段e的集合。該點集V的一個三角剖分T=(V,E)構成一個平面圖G。該平面滿足條件：

1)平面圖中的邊不包含點集中除了端點外的任何點；

2)沒有相交的邊；

3)平面圖中所有的面都是三角面，且所有三角面的集合是散點集V的凸包。

三角剖分在圖形學和建模中被廣泛使用，用來模擬復雜物體的表面。在三角剖分的基礎上，滿足空圓特性和最大化最小角特性的剖分稱為Delaunay剖分。即Delaunay三角形網中，任一三角形的外接圓范圍不會存在其他點且三角形的最小角最大。Delaunay三角剖分與Voronoi劃分互為對偶圖，如圖2所示。

圖2 點集的Delaunay三角剖分(實線)和Voronoi圖(虛線)

進行Delaunay剖分前，需要確定任務空間中障礙物的邊以及頂點和內角點的坐標值。三角剖分后，對障礙物內部的三角形區域進行標記并且從三角組網中剔除。剩下的三角形稱為自由三角形，組成自由空間。二維下的任務空間Delaunay三角剖分如圖3所示。

圖3 任務空間的Delaunay剖分

Delaunay三角剖分具有唯一性、最優性和規則性等優點，所以在對E100的任務空間進行建模中使用該方法，使得算法更加可靠。

2 加權函數和優化準則

在線性矩陣不等式約束的優化問題中，目標函數決定了哪一條路徑會被選中，所以，選擇可靠的目標函數至關重要。目標函數由兩個矩陣組成，權重矩陣和變量矩陣(將在第3部分中討論)。定義如下優化準則：

1)三角形的數量(WN)：在不考慮尺寸的情況下，從起點到終點的路徑盡可能地選擇三角形數量較少的一條；

2)三角形的面積(WA)：算法搜索的路徑盡可能地保證路徑中三角形組成的面積要小；

3)三角形的中線長(WM)：選取三角形的中線作為三角形中機器人的要走的路徑，并盡可能地保證中線長的和要短；

4)機器人尺寸約束(WR)：機器人穿過障礙物時，機器人的尺寸大于障礙物之間的距離時，障礙物之間的路徑不能被選擇。

將上述的準則進行加權組合，構成加權目標函數

W=α1×WN+α2×WA+α3×WM+α4×WR

(1)

用加權目標函數對路徑進行評價，以規劃出最優路徑。

準則3)中機器人通過三角形時，選擇三角形的連接兩條自由邊的中線作為路徑。自由邊位于Cfree自由區域中，不屬于任何障礙物的邊緣。這些中線代表各個三角形，中線長度的和作為目標方程中的一個權重。其中，對于起始點S和終點G，其連接相鄰三角形邊的中點所構成的路線SE和FG來取代中線，構成起始路徑和終止路徑。如圖4所示。

圖4 通道中的路徑

3 建立優化模型

定義具有如下形式的不等式為線性矩陣不等式

(2)

線性矩陣不等式的約束條件定義了自變量空間的一個凸集，即{X|F(X)<0}，所以，這是一個凸約束。線性矩陣不等式的這一性質使得其是求解線性凸二次規劃問題的有效方法。很多系統的最優化問題都可以轉換為基于線性矩陣不等式的凸或準凸優化，并且能夠解決很多沒有解析解的問題。線性矩陣不等式約束下的最優問題為：

minx∈Sf(x),f:S→R
s.t.F(x)<0

(3)

使用MATLAB內自帶的線性矩陣不等式(LMIs)求解器進行仿真運算。

使用二進制整數規劃法來描述Cfree中的三角形，即代表路徑規劃問題的目標函數的變量。所以，變量的二進制整數規劃(BIP)定義如下：

(4)

為了保證從起點到目標點的路徑連續，構建軌跡通道的三角形必須滿足如下條件：

3.2.2 醫患關系緊張 在訪談中，大部分醫護工作者都提到了影響自身職業認同水平的主要因素是緊張的醫患關系。“我們在醫院工作的人壓力都非常大，這種壓力并不是說醫學素養不夠、診治技能差，我們對自己非常有信心，壓力主要來自和病人之間的關系。”當前醫患關系緊張，甚至發生了多起襲醫事件，這導致部分醫護工作者對自身職業認同程度降低。“有一些病患誤解了醫護工作這個職業，覺得我們什么病癥都可以治好，這是不現實的想法”“我覺得在醫院工作，不論醫生還是護士，都是非常高尚的職業，我們也盡職盡責地幫助病患解除痛苦，但病患來醫院本來就帶著消極情緒，有時候不太理解我們的工作性質。”

1)起始點和終點的三角形必須被選中，分別為xS和xG；

2)如果一個三角形被選中(除了xS和xG)，則它相鄰的兩個三角形也必須被選中(連續性條件)；

3)起始和目標三角形只能有一個被選中的相鄰三角形(避免環回條件)；

4)為了避免環回，有三個自由邊的兩個相鄰三角形一定都被選中。

基于以上條件，求解最優軌跡的BIP模型描述為：

MinimizeJ=WT·X

s.t.

xS=1,xG=1,xi∈{0,1},i?{S,G}。

(5)

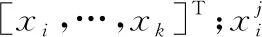
根據上述約束，所以軌跡規劃問題轉換為擁有k+p個約束的最優規劃問題(k+p-2個不等式和2個等式)，最優規劃問題的優化準則由方程J定義。

上述的最小化問題模型可以轉化為基于線性矩陣不等式約束的優化問題。目標方程為：

MinimizeJ=WT·X

(6)

式中Tk×1是變量[xi]的列向量；Wk×1是加權列向量。

對于約束方程，式(5)中的不等式和等式重新構造成擁有如下3個線性矩陣不等式的系統：

H=diag(AX-CX)≥0
U=diag(A′X-C′X)=0
V=diag(A″X-C″)≤0

(7)

上述的線性矩陣不等式經過解算后數值為1的變量代表最優路徑中的三角形，最優路徑從屬于Cfree空間中。直接使用二進制整數規劃進行求解得到的答案與使用線性矩陣不等式所得到的答案一樣，但使用線性矩陣不等式求解更簡單，速度也更快。

4 仿真實驗

構建巡檢機器人的工作環境，進行仿真，仿真結果如圖5所示。

圖5 最優路徑

由圖5可以看出最優通道中三角形的中線構成機器人運動軌跡。圖中橢圓形標注出的通道雖然可以獲得更加短的路徑，但由于機器人尺寸限制，該條通道不可選。

這里對規劃出的最優路徑進行一個優化。利用通道中的三角形構造凸多邊形。從起始三角形開始，增加相鄰三角形，直到組成的多邊形變凹。下一個凸多邊形從這個斷開的三角形開始，依次進行三角形的組合，將通道中的凸多邊形的邊的中點的連線作為運動軌跡，如圖6所示。

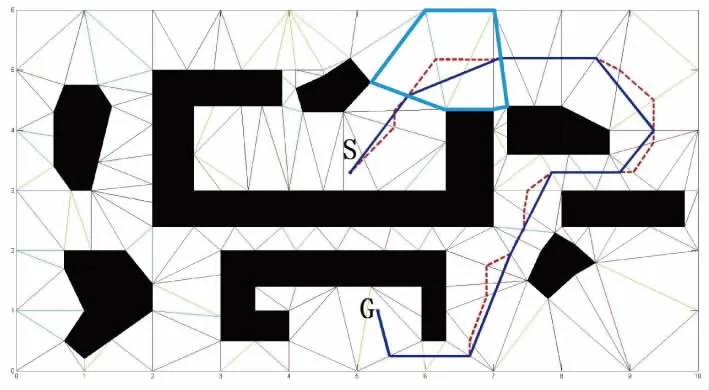
圖6 優化后的最優路徑

圖6中圈出的區域為多個三角形構成的凸多邊形，調整后的軌跡比原先中線構成的軌跡更短，而且凸多邊形也保證了兩條邊中點的連線在最優通道中，不會穿過障礙物。

最后對軌跡進行光滑處理，以使得機器人在運行中的轉向較為平緩，得到優化后的路徑曲線如圖7所示。

圖7 光滑處理后的最優路徑

在仿真實驗的基礎上，為了驗證本文方法高效性，構造多個工作環境，將本文方法的路徑規劃耗時和路徑長度與其他相近方法進行對比。這里選取與Delaunay三角剖分互為偶圖的Voronoi劃分，對任務空間進行劃分，并使用高效的Dijkstra算法對劃分后的任務空間進行最優路徑的搜索。任務環境之間以環境中障礙物的數量n為變量，從5～30遞增，每次規劃都進行多次計算仿真，取平均值。兩種方法對比仿真計算的結果如表1所示。

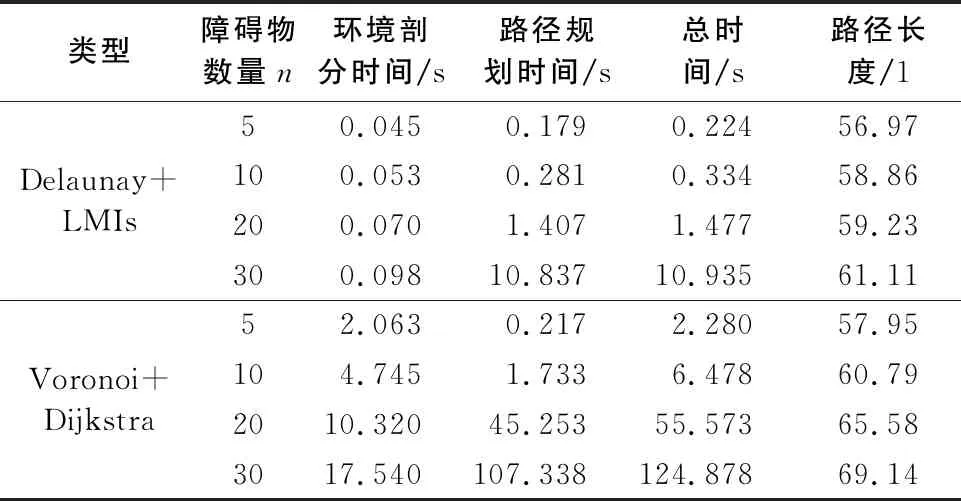
表1 規劃耗時和路徑長度

從表1中可以看出，本文的算法在路徑長度較短的情況下，規劃耗時也較短，尤其是障礙物數量較多時，規劃上的效率優勢更為突出。

5 結語

本文提出了一種基于線性矩陣不等式的巡檢機器人路徑規劃方法，并以E100巡檢機器人為例，構建任務環境，進行仿真，驗證了算法的正確性，同時與相近算法進行對比，驗證了高效性。本文的算法簡單、完備，考慮了路徑中的約束，且機器人不會陷入局部最小點。