讓數學核心素養在課堂落地生根

郭利鋒

一、現狀分析

練習課是一種重要的教學形式。教師經常抱怨，學生學習效率低下，導致教學存在困難。筆者反思發現：首先，教師缺乏對練習課的思考和設計;其次，教師缺乏新的教學思想;最后，教師缺乏解題策略的滲透與指導。筆者認為，教師要先以《新課程標準》理念統領教學思想，重視練習課設計，設計的習題要有深度、寬度;其次，練習課不僅要鞏固基本知識，幫助學生形成技能，還要讓學生掌握解題方法與策略，促進學生可持續發展。下面，筆者以六年級數學思維拓展練習為例。

二、教學目標

第一，在舊知的基礎上拓展延伸，經歷“再發現、再建模”的探究過程，發展學生的數學思維。

第二，讓學生逐步掌握解題方法與策略，達到舉一反三的能力，促進學生可持續發展。

第三，激發學生不斷探究知識的興趣，培養學生善于思考、勇于挑戰的思維品質。

三、教學實踐

在本節課中，筆者設計了闖三關活動，即三個題組。

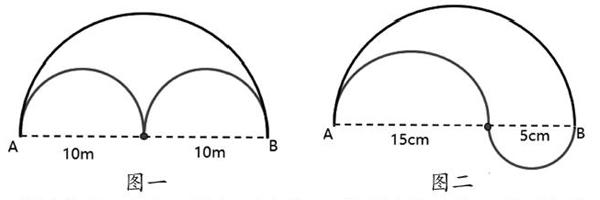
第一關：從A點到B點，有兩條路，你認為哪條路更近？為什么？（出示圖一）

教師問：“為了便于計算，你能用‘幾π的形式表示路的長度嗎？”

學生答：“兩條路一樣長，因為這兩條路的長度都等于10π。”

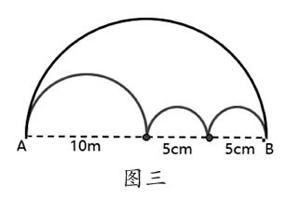
教師出示圖二，問：“現在兩條路還一樣長嗎？為什么？”

學生答：“兩條路還是一樣長，都等于10π。”

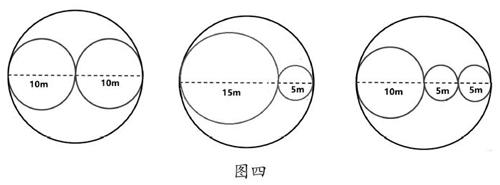
教師出示圖三后，學生異口同聲地說：“兩條路一樣長。”教師組織學生思考并討論：“觀察三個圖，有什么發現？”

學生1回答：“這些路都等于10π，都一樣長。”

學生2回答：“大圓周長的一半等于幾個小圓周長的一半。”

學生3回答：“我同意第二個同學的看法，但要在大圓直徑等于幾個小圓直徑和的情況下才行。”

教師追問：“如果把半圓變成整圓，這個規律還存在嗎？為什么？”（出示圖四）

學生1答：“規律依然存在，大圓的直徑是20m，周長就是20π，每個大圓中的小圓直徑的和也是20m，所以周長和也是20π。”

教師板書：當大圓的直徑等于小圓直徑的和時，大圓的周長等于每個小圓周長的和。

教師問：“大圓的直徑鋪滿2個小圓、3個小圓，大圓的周長都與小圓周長和相等，大圓的直徑上還能鋪滿幾個圓，是不是也有這樣的規律？”

教師引導學生展開想象，并推理得出4個、5個、6個……無數個。

教師出示練習：桌面上畫了一條80厘米的線段，還有直徑為1厘米、2厘米、3厘米、4厘米、5厘米、8厘米的圓形紙片若干，現在用圓形紙片將桌上線段蓋住，使紙片圓周長總和最短，這些圓周長總和最短是多少厘米？（如圖五所示）

教師組織學生討論“蓋住”“紙片周長總和最短”的含義，引導學生理解其中的含義，再類推整圓，解決實際問題，達到拓展規律和運用規律的目的。

第二關：觀察比較下圖六中陰影部分的面積，你有什么發現？

學生通過觀察比較、交流討論，發現可以把后面三個圖轉化與第一個圖一樣，用正方形面積減去圓的面積，剩下的陰影部分面積一定相等。

教師問：“如果正方形里面不是1個圓，而是4個、9個、16個圓，陰影部分面積還是相等嗎？”

學生答：“我猜測陰影部分面積是相等的。”

教師問：“怎么驗證？需要什么條件？”

學生答：“需要知道圓的半徑或直徑。”

教師問：“如果正方形邊長是12厘米，該怎么算？”

學生答：“只要算出4個圓與9個圓面積之和等于大圓的面積，陰影部分面積就會相等。”（如圖七所示）

教師引導學生獨立計算小圓面積的和，要求結果還是用“幾π”表示，做完后小組交流解題思路，并匯報。

學生說：“都是36π，第二個圖中4個小圓的面積之和是π×3×3×4=36π，第三個圖中9個小圓的面積之和是π×2×2×9=36π。”

教師說：“現在請你們想象正方形里鋪滿1個圓、4個圓、9個圓，剩下的陰影部分面積都相等，照這樣鋪，正方形里面還能鋪幾個？”

學生1說：“可以一排擺4個擺4排，就是16個。”

學生2說：“還可以擺25個，只要每排擺的個數和排數一樣就可以了。”

學生3說：“我認為n2個，因為1×1=1個 ，2×2=4個 ，3×3=9個，4×4=16個，5×5=25個……n×n= n2，所以是n2個。”

總結：根據數量關系S陰=S正-S圓解答，借助數形結合，通過轉化、計算或想象得到：因為每個正方形中的白色部分面積（圓的面積）是相等的，所以剩下的面積（如圖八所示）也是相等的。

第三關：擺n個三角形，需要幾根小棒？每增加一個三角形就增加幾根小棒？三角形的個數與小棒的根數有什么關系？你能不能用算式表示圖形規律？如圖九所示。

學生說：“小棒根數是1+2n或2n+1根。”

教師提問：“‘1+2n中的‘1表示什么？‘2和‘n又表示什么？”

學生答：“算式中的‘1表示第一根小棒，‘2表示每增加一個三角形就增加2根小棒，‘n表示三角形個數。”

教師問：“如果擺n個四邊形需要多少根小棒？n個五邊形、六邊形呢？（如圖十所示）”

學生類推得出：擺n個四邊形需要小棒1+3n根，擺n個五邊形需要小棒1+4n根，擺n個六邊形需要小棒1+5n根。

總結：這題先通過數形結合探究簡單圖形蘊藏的規律，再類推到相類似或相關較復雜的圖形中，找到解決這類問題的方法和策略。

全課總結：教師根據學生的匯報，引導學生歸納總結成思維導圖。

四、教學思考

這節練習課三個題組的教學有三個共同點：第一，教師引導學生從數形結合的視角經歷探究數學規律的過程，歸納規律、解釋規律、應用規律，通過解決一個問題，實現了解決一類問題，這就是建模過程;第二，教師通過不斷追問，引導學生進行類比，通過聯想、猜測，促進學生獨立思考和思維碰撞，讓知識與方法的遷移發生，這也是推理過程，可以培養學生的推理能力;第三，教師讓學生體會“數與形”之間完美結合帶來的直觀性和簡捷性，“形”中蘊含著數的規律，“數”可以用形呈現，體悟數形結合和化繁為簡的思想。

筆者原認為這節課內容較難，教學起來會比較吃力，但在實際教學中，學生思維異常活躍。通過觀察思考、比較探究、猜想驗證、想象推理、交流表達等，學生的思維得到了發散和拓展，也使學生在鞏固基礎知識和基本技能的基礎上掌握了解題的方法和策略，發展了解題能力和學習能力。

（作者單位：廣東省佛山市順德區聚勝小學）