航天服充氣壓狀態下的關節阻力矩特性研究

劉文樵，施 虎，譚 坤，張瑞明

(1.西安交通大學 機械工程學院，陜西 西安 710049；2.中國航天員科研訓練中心，北京 100094)

引言

隨著人類對太空探索的不斷深入，人類在太空和其他星球的作業任務也越來越多。由于太空環境復雜、惡劣，航天員在開展空間作業任務時需要穿著特定的航天服。因此，航天服的活動性能對航天員的作業效率至關重要。通常航天員在穿上航天服之后，人體與航天服之間的封閉空間充入一定壓力的氣體以構成真空防護，導致航天服內外形成余壓。

對于艙外作業而言，當航天員在作業過程中完成上肢和下肢彎曲運動時，此余壓會導致航天服關節處產生相當大的阻力矩[1]，從而降低了航天員肢體運動的靈活度、準確性及平衡性，增加體能消耗，嚴重制約了航天員的艙外作業能力與活動范圍[2]。因此，在設計制造階段，通過理論建模實現對航天服運動力學性能的準確預測，不僅能夠為航天員模擬訓練提供理論參考，而且對于研制具有關節助力功能的航天服具有重要意義。由于航天服在充氣壓狀態下屬于柔性體，其運動與力學特性呈現出高度的非線性，難以直接建立數學描述模型[3]。基于實驗測試的關節阻力矩和運動數據進行擬合建模是目前常用的研究方法。

在航天服關節阻力矩測試方面，目前國內外采用的測試方案主要分為內置式和外置式。內置式是目前在航天服工效學研究中采用的一種較先進的測量方法，如MIT采用內置式機器人RSST(Robotic Space Suit Tester)來測量EMU艙外航天服的關節阻力矩[4]，該方法由機器人直接驅動航天服各個關節運動，并由安裝在機器人中的位置、力矩等傳感器實時測量航天服各關節的轉角和阻力矩，測量精度較高，能對航天服多個關節同時進行測量。但由于每個測試機器人只適合單一種類和尺寸的航天服，對于不同種類和尺寸的航天服則需要調整或重新設計測量裝置，而且設備成本很高，可維護性相對較差，另外還會帶來操作安全性和航天服內衛生等問題[5]。外置式則是研究最多使用最廣泛的一種測量方法，目前外置式測量一般采用機械臂運動軌跡規劃和轉動軸自驅動扭矩測量2種方法。前者如哈爾濱工業大學的高志強等[6]提出的測量艙外航天服關節阻力矩采用外置式機器人，該方法需設計符合航天服關節運動特征的多自由度機械臂，并完成復雜的運動規劃與動力學推導問題，針對不同關節需要重新規劃，使得測量過程過于復雜化；而后者將航天服關節運動定義為沿固定轉動中心的旋轉運動，在轉動軸處設置轉動機構，使關節與身體連接一端固定，驅動轉動機構并通過轉動扭矩傳感器測量關節阻力矩，這種方式方便且能直觀測量關節力矩信息，如NASA[7-9]、中國航天員科研訓練中心[10]均采用這種方法，但在目前的自驅動測量方法中，航天服關節并非有固定的轉動中心，隨著關節彎曲角度變化航天服轉動中心會與機械機構轉軸中心偏移，由此會造成測量誤差。因此，基于以上方法的不足之處，本研究建立了一種通過簡易的龍門模組滑臺機構擬合航天服關節運動的測試平臺。該平臺通過擬合航天服關節彎曲運動軌跡，并由力傳感器采集運動過程的驅動力信息，得到航天服關節阻力矩，具有設備操作、維護較為簡單，可測量不同種類、尺寸的航天服的優點。

在航天服關節阻力矩的建模研究方面，由于艙外航天服關節材料和結構導致的遲滯特性，導致常規的數值擬合方法無法實現對阻力矩的準確描述[3]。目前國內外關于遲滯特性的研究主要是針對壓電陶瓷等智能材料以及氣動肌肉等驅動器件運動性能補償控制方面[11-12]，典型的遲滯模型主要包括以Bouc-Wen模型為代表的微分型模型，和以Preisach模型為代表的積分型模型[13]。目前關于航天服關節阻力矩遲滯模型大多基于后者進行改進。SCHMIDT P B[14]、NEJMAN A J[15]基于Preisach模型建立了航天服關節阻力矩-角度模型。在國內，李照陽等[10]也選擇使用Preisach模型描述航天服的遲滯特性；王曉東等[9]使用RBF神經網絡建立了基于Preisach模型的航天服力矩-角度模型。但是通過參數辨識得到Preisach遲滯模型的方法需要考慮的參數較多，計算時間長，需要大量的訓練才能使Preisach遲滯模型達到很高的精度[16]。念龍生等[17]提出了一種改進Preisach模型數值實現方法，為航天服關節阻力矩建模提供了新的思路。本研究通過結合改進Preisach模型數值實現方法與線性插值方法，建立了航天服關節阻力矩模型相較于參數辨識方法具有更大的便利性。

1 航天服關節阻力矩測試

1.1 測試原理

為了探究航天服關節在轉動過程中的阻力矩特性，本試驗方案采用了一種可以精確確定轉動角度，精確施加牽引軌跡的測試方法，如圖1所示。為了確保測試結果的準確性，試驗過程中旋轉中心和牽引力作用點及作用方向均不變。實際測試過程中，通過在如圖2 所示的龍門模組結構中兩垂直進給軸組成的測試平面內控制多組離散的運動軌跡點的位置來實現。

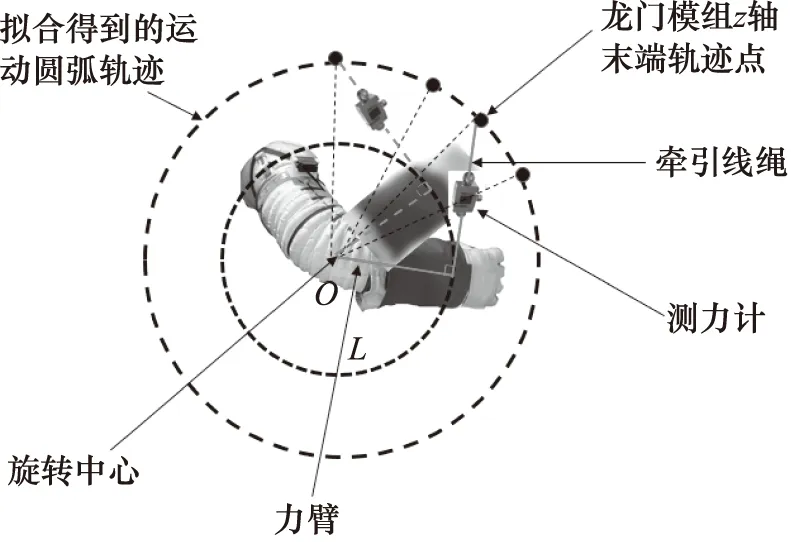
圖1 測試原理示意圖Fig.1 Schematic diagram of test principle

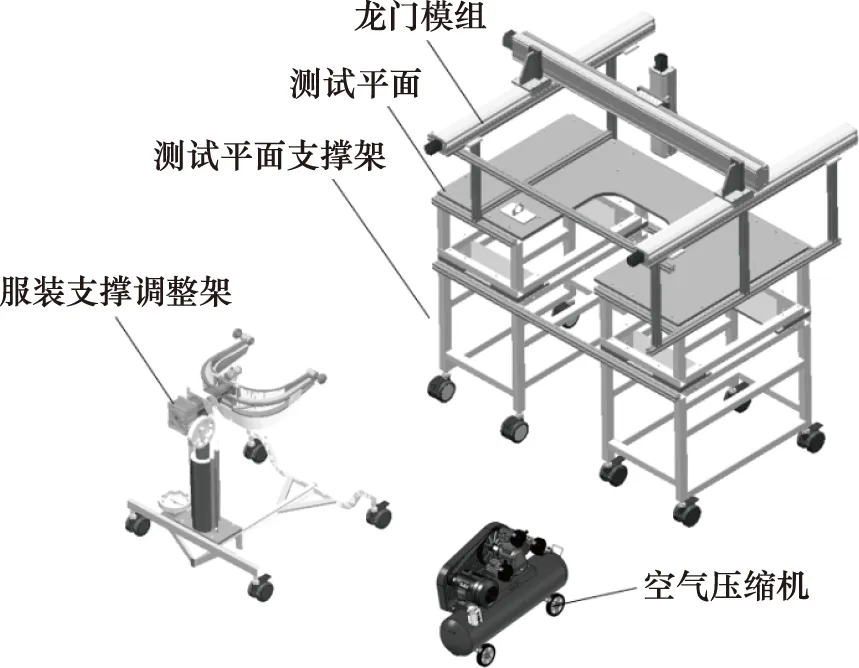
圖2 航天服測試平臺模型Fig.2 3D Model of spacesuit test platform

通過龍門式模臺滑組Z軸向的滑臺末端和關節牽引點連接，固定關節未活動一側，利用控制器控制龍門模組滑臺按照與力臂垂直的軌跡轉動。由于龍門模組做圓弧插補時的線速度是勻速，因此關節的轉動角度是與時間成正比的，同時由于航天服固定在測試平臺上，其活動角度可由龍門模組坐標計算得到，由此可精確確定轉動角度。通過測力計獲得試驗中的力數據后，關節力矩可以描述為：

M=F×L

(1)

式中，F—— 牽引作用點施加的力

L—— 力臂

M—— 牽引力對轉動中心O的力矩

針對航天服活動過程中的具體力臂長度與轉動中心難以準確確定的問題，該方法還可以對關節的轉動中心進行精確測量。由于龍門模組可以通過圓弧插補的方式牽引航天服實現圓弧運動軌跡，因此可以利用關節旋轉中龍門模組Z軸末端軌跡點的坐標推算出旋轉中心和半徑，同時也精確記錄出旋轉角度。在關節轉動過程中，可以利用模組控制器精確的記錄軌跡點坐標，再利用繪圖軟件，錄入軌跡點坐標，可以擬合一條圓弧軌跡線，通過該圓弧軌跡反推確定出中心和旋轉半徑。

在試驗平臺方面，通過調整航天服位姿，使測試關節的活動平面與測試平臺平行，以此抵消重力對試驗的的影響，并通過固定卡箍將關節活動端固定在牛眼滑車上，以此來避免關節活動時肢體與測量平臺的摩擦。

1.2 測試平臺的搭建

為了進行航天服關節力矩測試，結合航天服和測試場地條件自主研制了航天服力矩測試平臺，如圖2所示。該平臺主要由航天服支撐調整架、測試平面及支撐架、龍門模組及控制系統、充壓系統和測力系統等組成。

航天服固定支架及調節機構是進行航天服測試的基礎，其主要功能是以航天服軀干側銷座和前銷釘座為連接固定點，夾持固定航天服，并調整航天服的位姿。固定的航天服可以側向翻轉，與水平面平行。測試平面安裝于支撐架上，并配置一臺牛眼滑車用于消除摩擦對試驗結果的影響。根據牛眼滑車性能參數可知，其萬向滾珠平均摩擦系數為0.010～0.015，且航天服內為中空充氣狀態，牛眼滑車豎直方向上承受的作用力小于50 N，因此該摩擦力可以忽略不計。同時為了使關節在盡可能水平面內活動，不受重力干擾，應保證牛眼滑車高度與固定卡箍內圈最低點相同。龍門模組滑臺主要由4組絲杠螺母副組成，并由步進電機及電機驅動器進行驅動調節，由于步進電機啟停換向速度較快，因此對試驗結果的影響可忽略不計。滑臺兩端設有限位傳感器，便于滑塊模組的找零位。選用如圖3所示的PAC可編程自動化控制器作為龍門模組的控制系統，航天服關節的主要運動是圓周軌跡運動，使用此控制器可通過圓弧插補指令實現該運動軌跡。

圖3 PAC可編程自動化控制器控制面板Fig.3 PAC programmable automation controller panel

本試驗采用OTS-750x2-50L靜音無油空氣壓縮機作為氣壓發生裝置，提供給航天服所需要的試驗內壓強環境，試驗時需要先通過頂端的開關給壓縮機充入氣體，然后再將氣體從壓縮機通過氣體管路充入航天服內。最終以航天服上壓力表作為充壓是否結束的衡量標準，設定試驗所需的壓力。同時為了系統的安全考慮，設置了快速泄壓裝置作為試驗保障。

測試現場如圖4所示。測力系統主要采用LMN-6850型手持式測力儀。試驗時，龍門模組通過測力傳感器帶動航天服關節運動，并實時進行數據采集與存儲。同時，該測力計由螺栓通過橫向插入方式與航天服關節處的卡箍連接，由此保證測量過程中拉力計與航天服力臂垂直，如圖4a所示。

圖4 現場試驗圖Fig.4 Field test

1.3 測量步驟及結果分析

本次試驗主要測試了航天服的肘關節、膝關節、髖關節，如圖5所示，具體測試步驟為：將航天服固定于支撐架上，通過航天服調節機構調整航天服的高度和位姿，使得航天服測試關節平行放置在測試平板上，抵消重力影響；通過壓縮機給航天服充壓，得到不同余壓測試環境；通過固定卡箍將關節不動端固定在測試平板上，通過固定卡箍將關節活動端固定在牛眼滑車上；將龍門滑組的Z軸立柱與關節活動端的固定卡箍通過測力傳感器相連，通過龍門滑組進行圓周運動帶動關節進行相應的圓周運動；并通過測力計上位機軟件實時采集關節力數據。

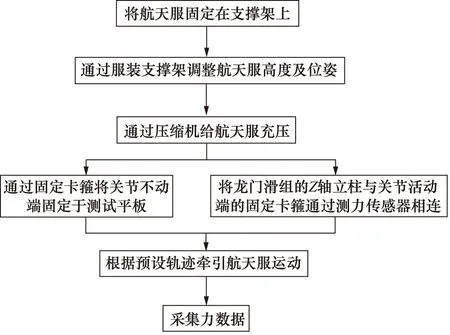
圖5 測量步驟Fig.5 Measurement steps

為探究航天服余壓及關節活動速度對關節阻力矩的影響，設計了2組試驗。

第1組試驗為相同關節活動速度、不同航天服余壓條件下的測量。由于航天服的最低工作余壓為0.010 MPa，登月服的工作余壓為0.025 MPa，正常艙外航天服的工作余壓為0.040 MPa，因此分別測量肘關節、膝關節、髖關節在這3種余壓條件下活動時的關節力矩。其中，測量肘關節時，龍門模組絲杠速度為600 mm/min，關節從0°活動至最大角度再活動至0°共測量12個周期，初始最大測量角度為60°，每個周期的最大角度以5°遞減；測量膝關節時，龍門模組絲杠速度為1000 mm/min，關節從0°活動至最大角度再活動至0°共測量13個周期，初始最大測量角度為65°，每個周期的最大角度以5°遞減；測量髖關節時，龍門模組絲杠速度為600 mm/min，關節從0°活動至最大角度再活動至0°共測量8個周期，初始最大測量角度為40°，每個周期的最大角度以5°遞減。阻力矩大小隨時間變化的關系如圖6所示。

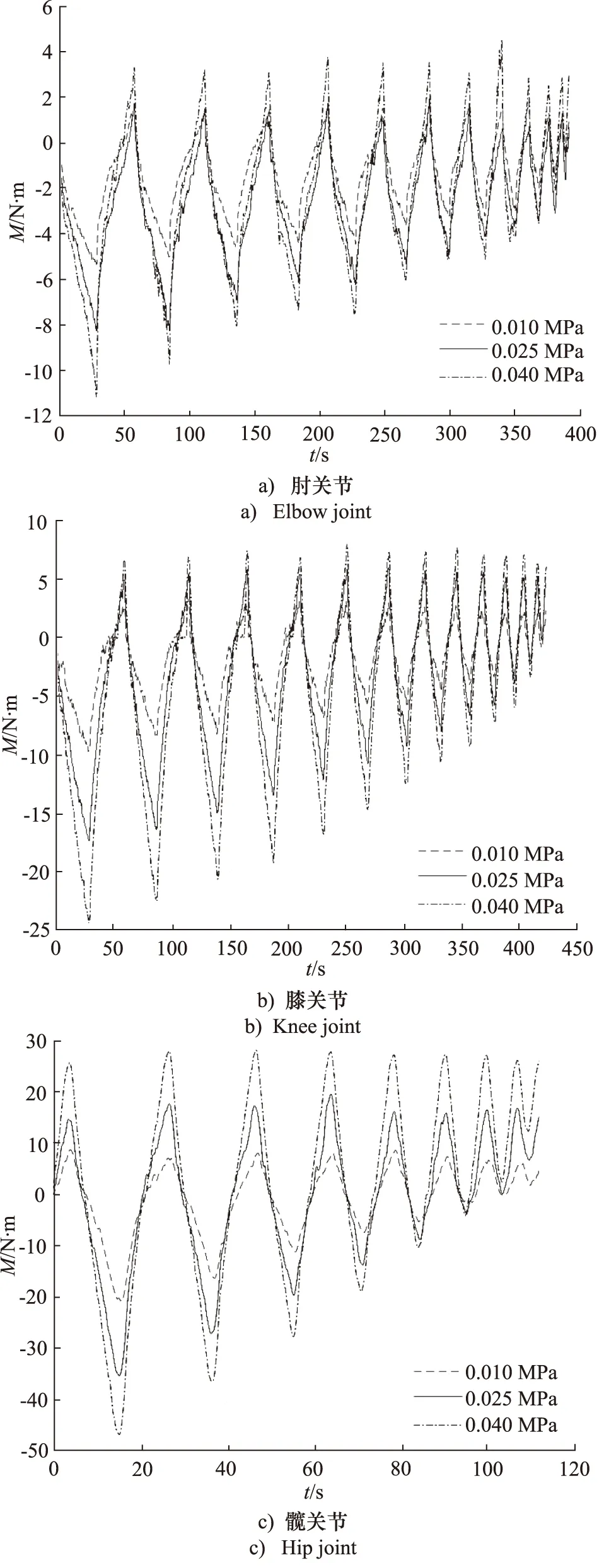
圖6 不同氣壓下各關節阻力矩隨時間變化關系Fig.6 Relation of resistance moment of joints with time under different air pressures

第2組試驗為相同航天服余壓、不同關節活動速度條件下的測量。將航天服余壓控制在0.040 MPa，并分別測量了肘關節、膝關節、髖關節在不同活動速度條件下活動時的關節力矩。其中，測量肘關節時，龍門模組絲杠速度分別為1000, 1400 mm/min，關節從0°活動至最大角度再活動至0°共測量12個周期，初始最大測量角度為60°，每個周期的最大角度以5°遞減；測量膝關節時，龍門模組絲杠速度分別為600, 1000 mm/min，關節從0°活動至最大角度再活動至0°共測量13個周期，初始最大測量角度為65°，每個周期的最大角度以5°遞減；測量髖關節時，龍門模組絲杠速度分別為600, 1000 mm/min，關節從0°活動至最大角度再活動至0°共測量8個周期，初始最大測量角度為40°，每個周期的最大角度以5°遞減。阻力矩大小隨時間變化的關系如圖7所示。

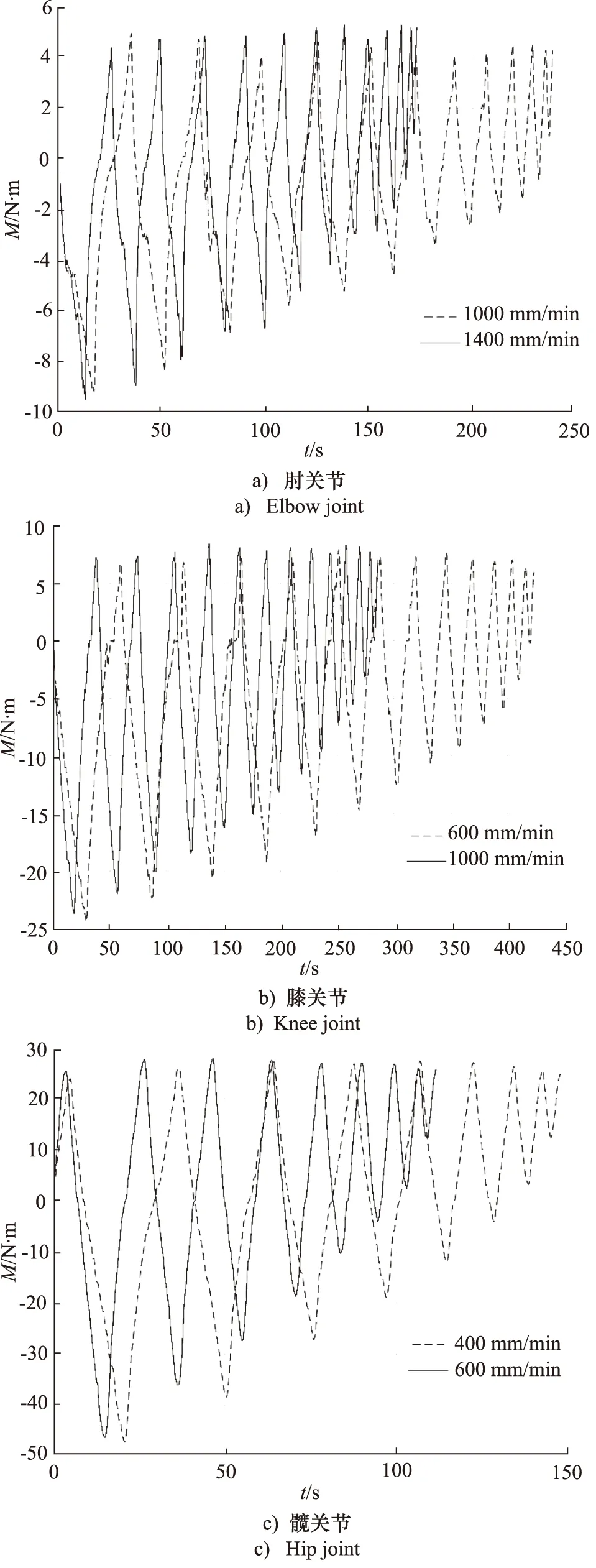
圖7 不同速度下關節阻力矩隨時間變化關系Fig.7 Relation of resistance moment of joints with time at different speeds

在這2組試驗中，關節活動角度的增加階段與減小階段關節力矩變化均出現了不對稱，體現出了明顯的遲滯特性。同時，在航天服關節活動的過程中，當關節角度從極限位置減小到某一個值時，航天服便無法靠自身彈性恢復到初始位置，此時為了使航天服繼續活動，需要對航天服施加一個相反方向的力。由第1組試驗結果可知，關節阻力矩大小與航天服余壓正相關，航天服余壓越大關節阻力矩也越大，而由第2組試驗結果可知，關節阻力矩與關節活動速度無明顯關系。

2 航天服關節阻力矩遲滯特性建模

在獲得航天服肘關節、膝關節、髖關節的關節阻力矩試驗數據后，本研究采用遲滯模型中較為經典的Preisach模型進行建模，并在其基礎上提出了通過結合改進的Preisach數值實現方法與線性插值來實現該模型的方法。

2.1 Preisach模型原理

經典Preisach模型由Ferenc Preisach為解決鐵磁材料中的遲滯現象而提出，由多個具有不同權重的基本遲滯變換函數疊加構成，其數學表達式為：

(2)

其中，u(t)表示t時刻輸入的角度；M(t)表示t時刻輸出的力矩；γα,β為基本遲滯變換函數，α和β(α>β)分別表示輸入向上和向下變換的變換點，在該模型中，基本遲滯變換函數的值為1或-1；α和β分別是航天服關節彎曲過程中的角度增加量和減小量；μ(α,β)是γα, β的權重函數。

目前關于航天服關節力矩的研究中普遍使用了參數辨識的方法對權重函數μ(α,β)進行辨識，該方法需要大量訓練樣本，耗時較多，精度較難保證。采用線性插值擬合的數值實現方法可以很好解決這一問題。

經典Preisach模型具有擦除性和一致性2個特性，一致性指的是極大值與極小值相等的閉合遲滯曲線一致，擦除性指當輸入大于歷史上的極大值或者小于歷史上的極小值時，模型會擦除這些歷史極值，以新的輸入為極值。

2.2 航天服遲滯特性建模

經典的Preisach模型數值實現方法不具有擦除特性，當輸入大于歷史極大值或小于歷史極小值時，經典數值實現方法的計算結果與模型實際輸出值有較大誤差，因此無法適用于輸入變化過程較為復雜的場景。為了解決此問題，念龍生等[17]在原有的Preisach數值實現方法基礎上，通過加入歷史極值數組，提出了一種具有擦除特性的改進Preisach數值實現方法，其具體表達式如下：

(3)

其中，數組α和β分別為極大值遞減數列和極小值遞增數列，在角度增加階段與減小階段轉換時，將極大值和極小值分別存儲在極大值數組和極小值數組中，使該實現方法具有記憶性；n與數組大小相關；u(t)為實時輸入角度值，u′(t)為輸入角度的導數，α′,β′為數組α和β中的值；擦除函數g1和g2分別不斷更新數組α和β及n，使這個數值實現方法具有擦除特性。

為了便于預測航天服關節在活動過程中輸出的力矩，首先將Preisach平面離散化，如圖8所示。然后通過試驗獲得航天服余壓為40 MPa時，關節從初始位置活動至等分滿程角度所輸出的力矩，建立離散平面上每個節點對應的α-β插值曲面，如圖9所示。

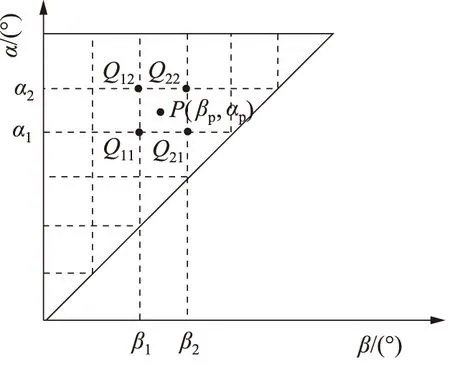
圖8 離散化的Preisach平面Fig.8 The discretized Preisach plane

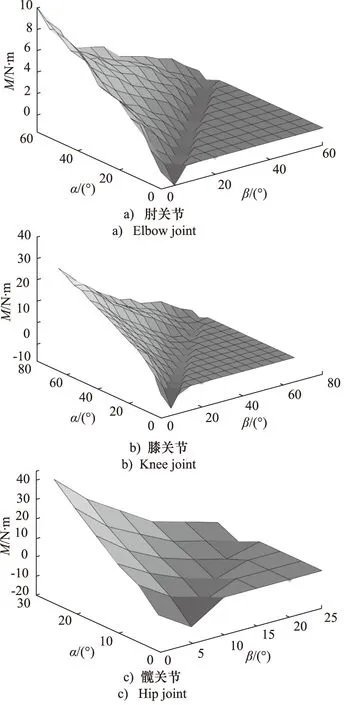
圖9 各關節上升角度α、下降角度β與力矩關系Fig.9 Relationship between ascending angles α and descending angles β of each joint and torque

對于航天服活動過程中任意不處于等分點上的力矩-角度點P(βP,αP)，由雙線性插值法原理可得：

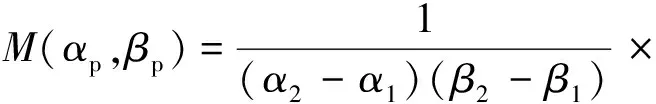
(4)

由式(4)可求得任意一點的輸出力矩。具體流程如圖10所示，在對模型進行離散化以后，當模型接收到輸入角度時，首先判斷輸入角度相比上一個輸入角度是增加還是減小，完成極值數列的更新；然后依據數組信息辨識該輸入角度在離散Preisach平面上所處的位置，進行雙線性插值，求解出該輸入角度值所對應的輸出力矩值；最后輸出力矩值，完成一次對應求解。

圖10 模型求解流程

2.3 模型驗證

依據上述模型實現方法，通過MATLAB/Simulink建立航天服關節模型，如圖11所示。將關節的活動范圍輸入到模型中，在該仿真中，各關節活動范圍分別為：肘關節0.14 °～46.74 °，膝關節0 °～24 °，髖關節0 °～16.91 °。 將得到各關節的仿真力矩與試驗測得的關節力矩進行比較，結果如圖12所示。通過仿真結果與試驗測量結果的比較，肘關節與髖關節的仿真關節阻力距變化與試驗數據較為吻合，膝關節的仿真力矩在關節活動至18°時隨時間的增加較慢。3個關節活動過程中仿真力矩大小與試驗數據的平均相對誤差分別為：肘關節3.41%、膝關節6.02%、髖關節0.75%。仿真模型對肘關節、膝關節、髖關節活動中的關節阻力矩預測值基本與試驗數據吻合，力矩變化趨勢基本一致，因此，該仿真模型能有效預測航天服關節活動阻力矩。

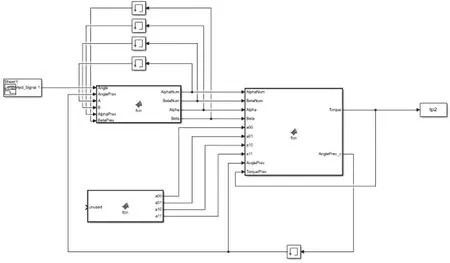
圖11 Simulink仿真模型

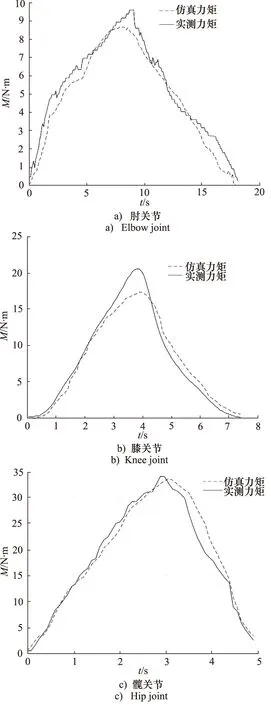
圖12 各關節仿真力矩與實驗力矩對比Fig.12 Comparison of joint torques obtained by simulation and experiment

3 結論

(1) 本研究在分析艙外航天服關節阻力矩特性的基礎上，研制了一套航天服關節阻力矩測試平臺，通過擬合航天服關節彎曲運動軌跡，并由力傳感器實時采集關節驅動力，得到航天服關節阻力矩，該平臺結構簡單，操作方便，可適用于不同種類、尺寸的航天服，在該平臺上開展了航天服運動特性、力學特性測試，測試結果表明，關節阻力矩大小與航天服余壓正相關，航天服余壓越大關節阻力矩也越大，而關節阻力矩與關節活動速度無明顯關系；

(2) 提出了一種基于雙線性插值的Preisach模型數值實現方法，基于試驗數據建立了航天服關節阻力矩遲滯模型，相較于常規的參數辨識方法，本研究改進的遲滯模型具有求解速度更快，所需試驗數據樣本更少的特點，模型預測與測試對比結果表明，模型能有效預測服裝關節活動阻力矩，肘關節的平均相對誤差為3.41%、膝關節的平均相對誤差為6.02%、髖關節的平均相對誤差為0.75%，為航天服運動力學性能的準確預測提供了理論支撐。