基于高斯過程的閥控非對稱液壓缸模型預測控制

孫 浩，陶建峰，余宏淦，劉成良

(上海交通大學 機械與動力工程學院，上海 200240)

引言

閥控非對稱液壓缸系統具有結構緊湊、空間布置靈活、功率密度大等特點，廣泛應用于工程車輛、加載試驗臺、機械臂等設備，多采用比例/伺服閥作為控制元件，實現閉環力/位置/速度控制。控制閥的非線性、液壓缸的不對稱性及負載擾動等強非線性因素會造成系統響應滯后、輸出超調、運動不平穩等，如何從控制方面解決上述問題是眾多學者研究的方向[1-3]。

丁問司等[4]采用粒子群優化算法實現模糊控制參數尋優，在線調整PID參數，有效抑制了油液含氣量的增加對位控系統動態特性的影響，但并未解決超調問題；LINJAMA M等[5]設計了基于模型的串級PID控制器，避免了因負載質量和體積模量造成的延遲特性，實現了精確的力/位置控制；JIANPENG S等[6]為實現挖掘機動臂平穩運行和精確位控，提出了基于模式切換的速度和位置組合控制策略，在能量損耗、動態特性和抗負載擾動方面均取得了很好的效果；KIM K等[7]以動臂速度場為優化目標，考慮泵流量約束，實現了變工況下速度的最優控制；HAO Y等[8]采用滑膜控制實現了位控系統的軌跡跟蹤控制，在有限時間內保證了誤差的收斂性，局限于無負載擾動工況；金坤善等[9]采用擴張觀測器實時估計綜合擾動和狀態，提出了一種二階線性自抗擾策略，可以有效抑制不確定性擾動對控制系統的影響；何常玉等[10]利用動態面方法，并引入一階濾波器設計控制器，解決了反步法的復雜爆炸問題，提高了系統的位置精度和魯棒性。與采用普通PID相比，上述研究在相應工況下，均實現了很好的控制效果，提高了系統的控制精度和魯棒性，但當系統在滿足快速性或負載發生變化時，輸出會伴有超調現象，導致閥芯在零位附近切換，由于非對稱液壓缸伸出和縮回工況的動態特性不同，控制效果則會變差。模型預測控制由于可以處理復雜約束條件，是解決上述問題的有效控制方法。熊志林等[11]采用狀態估計設計了模型預測控制器，使用卡爾曼濾波器減小實際系統噪聲對狀態估計的影響，根據物理方程建立了線性預測模型，為消除其與實際模型間的誤差，引入了積分行為。由于閥控非對稱缸系統非線性問題突出，采用線性模型會存在一定局限性，而機器學習方法具有處理非線性問題的能力，可以很好的應用于復雜建模方面。楊泰春等[12]采用支持向量回歸辨識系統非線性模型，進一步提高了預測模型的精度，減少了系統的穩態誤差，但局限在于未考慮實際采集信號混有噪聲的影響，超參數需調試確定，預測模型的輸出值無法解釋。高斯過程回歸與支持向量回歸相比，優勢在于考慮了混有噪聲的訓練集樣本，超參數可自適應獲取，預測的輸出值具有概率意義，所需樣本數量少[13]。

本研究首先介紹了液壓系統和模型預測控制器的原理，推導了高斯過程回歸建模、核函數及超參數選擇過程；然后，以建立的非線性仿真模型為研究對象，進行模型預測控制器的設計，根據核函數和訓練集數據確定了超參數，采用高斯過程回歸訓練得到了非線性離散數學模型；最后，仿真分析了高斯過程回歸訓練模型的精度和模型預測控制器的控制效果。

1 液壓系統及控制器介紹

1.1 液壓系統工作原理

本研究的液壓系統適用于裝配用機械臂的驅動關節，定位精度需滿足±0.1 mm。部分液壓系統原理如圖1所示，由電液伺服閥1、溢流閥2(安全閥)、液壓缸3(帶磁致伸縮位移傳感器)、鎖緊閥4(到達目標位置通電即鎖緊液壓缸)、壓力傳感器5、位移傳感器6組成。油源為恒壓變量泵，伺服閥開口和液壓缸承受的負載決定了液壓泵的輸出流量。伺服閥的指令信號為-10～10 V，閥芯位移與其成正比，在指令信號為10 V 時，閥芯位于閥口P至A和B至T全開(100%)位置，液壓油流入無桿腔，活塞伸出，另一側同理。控制器根據采集到的位置信號和期望的輸入信號，計算輸出信號作用于伺服閥，以實現對系統的位置控制。

1.電液伺服閥 2.溢流閥 3.液壓缸 4.鎖緊閥5.壓力傳感器 6.位移傳感器圖1 液壓系統原理圖

當液壓缸輸出存在超調時，即使在穩態時達到定位精度要求，但在動態調整過程中會損壞具有配合要求的安裝面，這在實際中是不允許的。因此，采用模型預測控制建立液壓缸位置不超過期望值和伺服閥閥芯始終在單邊工作的約束，可以解決閥控非對稱缸系統輸出超調和控制效果變差的問題。

1.2 模型預測控制器原理

模型預測控制器是基于預測模型設計的，本質為求解多約束條件下二次規劃問題的過程，結構如圖2所示，需建立離散數學模型，根據當前時刻實際系統位置輸出和下一時刻伺服閥指令電壓(模型預測控制器輸出)及負載力，得到下一時刻預測模型位置輸出，為減小預測模型與實際系統的誤差，采用機器學習中的高斯過程回歸辨識實際系統非線性模型，將其作為非線性等式約束；保證伺服閥指令電壓范圍為-10～10 V，預測模型位置輸出不超過期望位置輸入，分別將其作為線性不等式約束；未來有限時刻預測模型位置輸出需高精度跟蹤期望位置輸入，伺服閥指令電壓不能變化過快，以此建立二次型優化目標函數，采用最優化方法在有限時域范圍內不斷滾動求解，將每次計算出的第一個最優指令電壓值輸出給實際系統。

圖2 模型預測控制器結構

2 高斯過程回歸建模

高斯過程回歸是以貝葉斯理論為基礎的機器學習方法，目的是求出預測輸出值的后驗概率分布，根據其均值和方差可以得到具有置信區間的預測輸出結果。

2.1 高斯過程回歸推導

閥控非對稱缸系統輸入與輸出的關系是非線性的，可以選擇合適的非線性變換將該系統的輸入特征映射到高維空間，使其在高維空間中變為線性可分的問題，n維輸入xl=[xl,1,…,xl,u,…,xl,n]T單輸出的非線性函數f(xl)，可以在高維空間中線性表示為：

f(xl)=qTw=μ(xl)Tw

(1)

式中，μ即為非線性變換，q=μ(xl)為變換后映射到m維空間后的向量(m?n)，w為權重向量，w∈Rm，xl,u為u特征下的值。

實際在處理回歸問題時，需考慮訓練集中輸出值存在的噪聲，實際輸出值可以表示為：

y=f(xl)+λ=μ(xl)Tw+λ

(2)

式中，λ表示訓練集中輸出值混有的噪聲項，假設其服從N(0,σ2)。

該非線性回歸問題需根據采集的數據(訓練集)得到權重向量。根據式(2)及噪聲λ分布可以寫出輸出樣本條件概率密度函數：

(3)

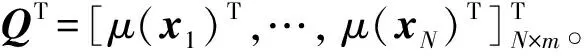
權重向量w存在先驗分布，假設其服從均值向量為0，協方差矩陣為G的多元高斯分布，則：

(4)

權重向量w的后驗概率分布為：

(5)

式中，p(Y|X)為邊緣概率密度。

式(5)可以由式(3)和式(4)表示為：

p(w|X,Y)∝p(Y|X,w)p(w)

(6)

式中，w′=σ-2(σ-2QQT+G-1)QY。

可知權重向量w的后驗概率分布服從均值為w′，協方差矩陣為L-1的多元高斯分布：

p(w|X,Y)～N(w′,L-1)

(7)

其中：

L=σ-2QQT+G-1

(8)

當有測試集輸入時，可以使用式(7)進行回歸預測，規定測試集原始n維輸入為x*，經非線性變換后為q*=μ(x*)，則預測輸出y*的概率分布為：

(9)

整理得預測輸出y*的概率分布服從：

N(σ-2μ(x*)TL-1QY,μ(x*)TL-1μ(x*))

(10)

根據式(8)，L逆矩陣可整理為：

L-1=G-GQ(σ2E+QTGQ)-1QTG

(11)

令K=QTGQ，k(x*,x*)=μ(x*)TGμ(x*)，k(x*,X)=μ(x*)TGQ，k(X,x*)=QTGμ(x*)，將式(11)帶入式(10)中，整理得：

σ-2μ(x*)TL-1QY=k(x*,X)(σ2E+K)-1Y

(12)

μ(x*)TL-1μ(x*)=k(x*,x*)-

k(x*,X)(σ2E+K)-1k(X,x*)

(13)

上述K,k(x*,x*),k(x*,X),k(X,x*)項是以非線性映射函數μ(x)的內積形式表示，可定義為核函數。

2.2 核函數及超參數確定

核函數可以將高維特征空間中的向量內積運算轉化為原始低維空間中的函數計算，極大的降低計算量。選擇合適的核函數，根據給定的訓練數據按概率估計最優超參數后，2.1節中所述的高斯回歸過程便可用于訓練模型并進行預測，其中，估計最優超參數的過程為求解無約束多變量極值問題。

本研究選擇最常用的高斯徑向基核函數：

式中，xa和xb表示原始空間n維輸入向量；γ2表示高斯核函數幅值；α表示特征長度尺度，對所有基函數的作用效果均相同。

高斯核函數可寫成如下形式：

式中，xa,u和xb,u分別表示對應的第u維分量。

模型超參數集合表示為Ω=[γ,α,σ]T，可采用極大似然法，求取似然函數極值來估計超參數。根據式(2)、噪聲λ和權重向量w分布可以寫出向量Y服從N([0]N×1,[K(X,X)+σ2E]N×N)。以訓練集輸出值的邊緣分布函數的負對數作為似然函數：

L(γ,α,σ|X,Y)=-ln(P(Y|X))=ξ(γ,α,σ)

(16)

將求解概率乘積的極大值轉化為求解無約束多變量極小值問題。

3 模型預測控制器設計

閥控非對稱缸系統的模型預測控制器原理如圖3所示。該控制器是以辨識的高斯過程回歸模型為基礎，通過求解二次規劃問題，得出最優控制值作用于系統。

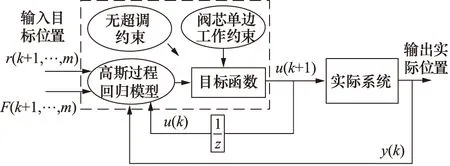
圖3 模型預測控制器原理

3.1 高斯過程回歸模型辨識與預測

定義當前時刻為k，下一時刻為(k+1)，非對稱閥控缸系統的離散數學模型為：

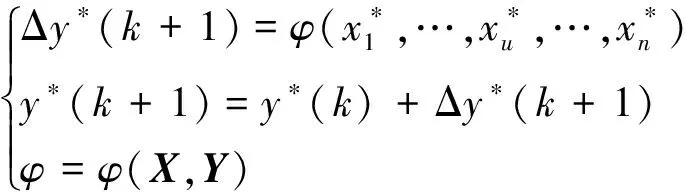
(17)

首先選擇高斯徑向基核函數，根據訓練集輸入和輸出樣本，建立輸出樣本Y的似然函數式(16)，采用最速下降法求解損失函數的極小值，得到超參數Ω=[γ,α,σ]T，最優超參數值隨訓練集樣本數量的改變自適應變化。

然后，計算訓練集的核矩陣：

當輸入測試集x*時，與訓練集樣本點的核向量為：

k(x*,X)=k(X,x*)T=[k(x*,x1)…k(x*,xN)]

(19)

3.2 二次規劃問題構建

1) 目標函數

本研究的非對稱閥控缸系統需實現精確的位置控制，同時需保證控制器輸出的電壓值變換平穩，目標函數可以用以下二次型表示：

(19)

式中，γ,ρ分別為位置權重和控制權重；y*(k+u)為(k+u)時刻預測位置輸出值；r(k+u)為對應時刻位置參考值；u(k+u)為(k+u)時刻電壓值；u(k)為k時刻電壓值；m，n分別為位置時域長度和控制值時域長度。

2) 約束

考慮液壓缸在任意位置運動，建立無超調輸出約束：

(20)

為實現伺服閥閥芯在工作時不換向，建立輸入約束：

(21)

綜上所述，根據優化目標函數式(19)，考慮線性不等式約束式(20)和式(21)，非線性等式約束式(17)，采用序列二次規劃方法求解二次規劃問題，[y*(k+1),…,y*(k+m),u(k+1),…,u(k+n)]T為最優解，以第一個控制值u(k+1)作為控制器輸出。

4 仿真驗證

本研究僅進行仿真驗證，采用文獻[14]的閥控非對稱缸系統的狀態方程，選擇零開口伺服閥，視其為二階振蕩環節，忽略恒壓變量泵的動態特性，建立輸入為控制電壓和外負載力、輸出為活塞位置并混有高斯白噪聲的連續時間非線性數學模型。從該模型中采集訓練集和測試集樣本，并驗證控制器效果。以活塞伸出工況為例，相關技術參數如表1所示，其他仿真參數見表2。

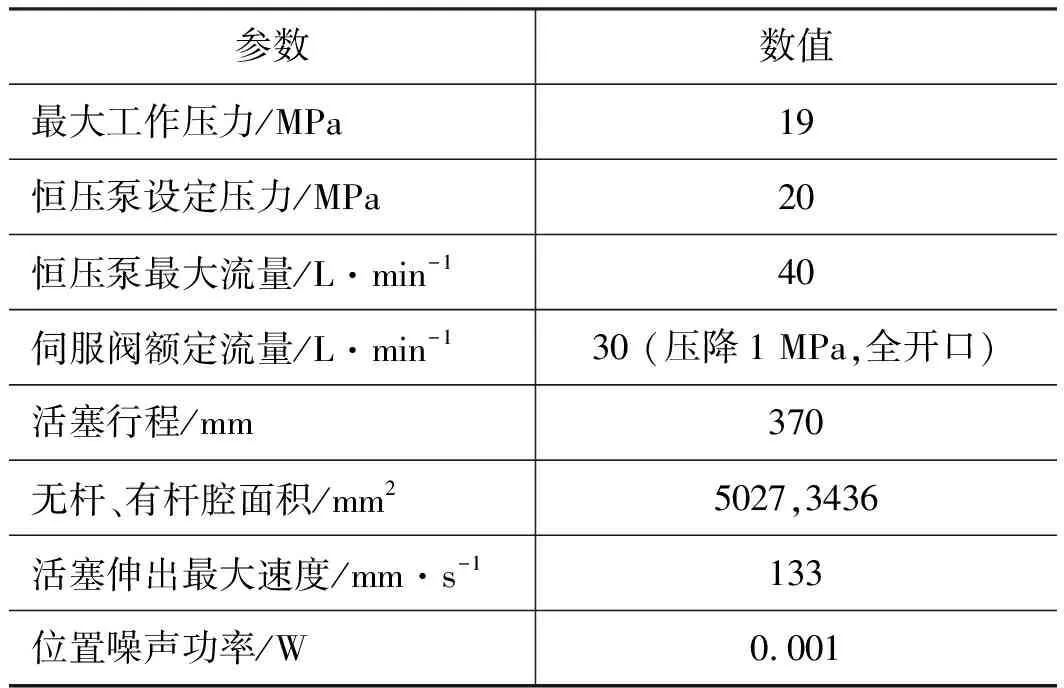
表1 相關技術參數

表2 閥控非對稱缸系統模型參數

4.1 高斯過程回歸模型精度驗證

采集閥控非對稱缸系統數學模型時域范圍階躍響

應數據，輸入電壓0～10 V，間隔1 V，輸入負載0～90 kN，間隔10 kN，輸出位置0～370 mm，時間間隔0.05 s。將上述數據離散化處理，得到訓練集樣本，由于輸入特征量綱不同，數值間差別過大，為提高模型訓練精度，對輸入特征進行零均值規范化處理，處理后的特征數據均值為0，方差為1，歸一化后的訓練集輸入樣本為：

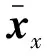
根據2.2中選擇的高斯徑向基核函數，及上述歸一化后的訓練集數據，便可進行超參數尋優，設置初始值Ω0=[0,0,-1]T，得到最優超參數為Ω=[2.259,0.754,0.710]T，進而訓練模型。為驗證模型的泛化能力，隨機選擇測試集工況如表3所示，得到預測輸出曲線如圖4～圖7所示。

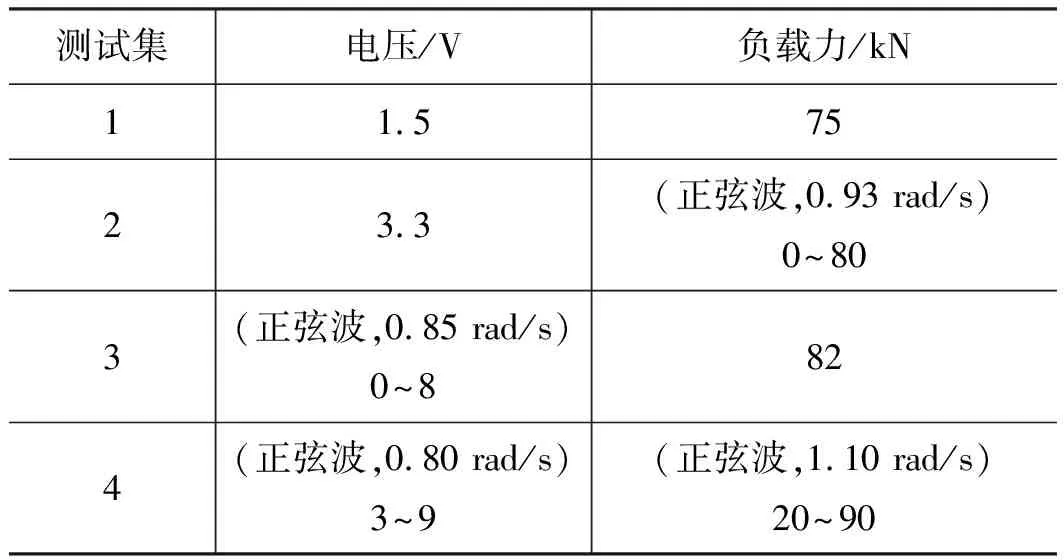
表3 測試集輸入參數

從圖4～圖7計算出測試集輸出的均方誤差、輸出噪聲的實際標準差，如表4所示。

圖4 測試集1預測輸出(位移增量)曲線

圖5 測試集2預測輸出(位移增量)曲線

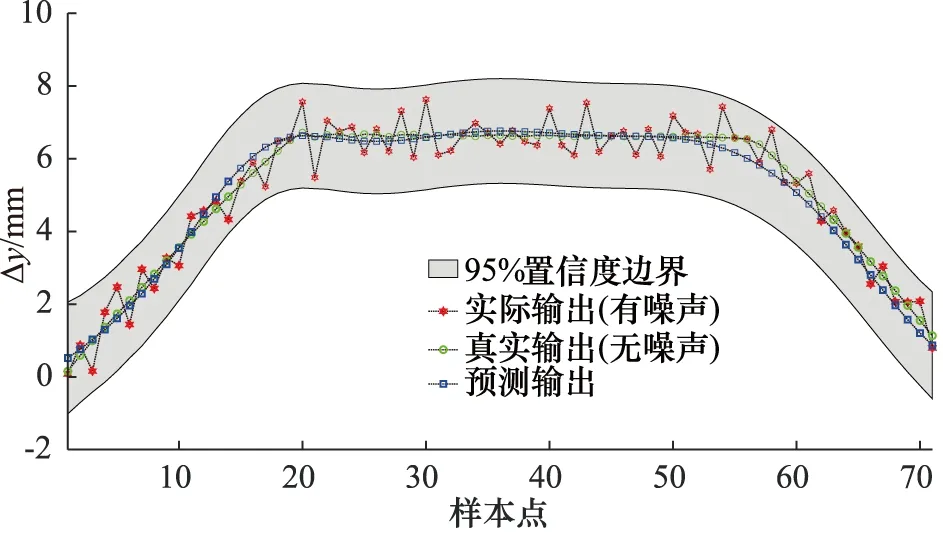
圖6 測試集3預測輸出(位移增量)曲線

圖7 測試集4預測輸出(位移增量)曲線

表4 4類測試集預測輸出結果

采用高斯過程回歸訓練模型，可以得到預測輸出值的置信區間，超參數根據核函數和訓練集自適應獲取，樣本集允許存在噪聲，對預測輸出的噪聲有很好的估計，訓練后的離散模型能精確的預測非對稱閥控缸系統真實輸出，并具有很強的泛化能力，可以用作模型預測控制中的非線性等式約束。

4.2 模型預測控制算法驗證

模型預測控制器實質是求解二次規劃問題，設置3.2.1節中目標函數的位置參考值為160 mm，初始電壓為0 V，位置時域長度m=10，控制值時域長度n=5，位置權重和控制權重的取值直接影響尋優速度，取γ=10，ρ=1；不等式約束需滿足3.2.2節中要求；3.1節中非線性等式約束初始位置為0 mm，訓練集樣本的均值和標準差分別為：

(23)

采用序列二次規劃算法求解上述二次規劃問題。仿真中設置控制器時間間隔為0.05 s。

為對比所提控制算法與PID控制在系統滿足快速性或負載發生變化條件下的控制效果，設置工況條件及對應PID參數如表5所示。

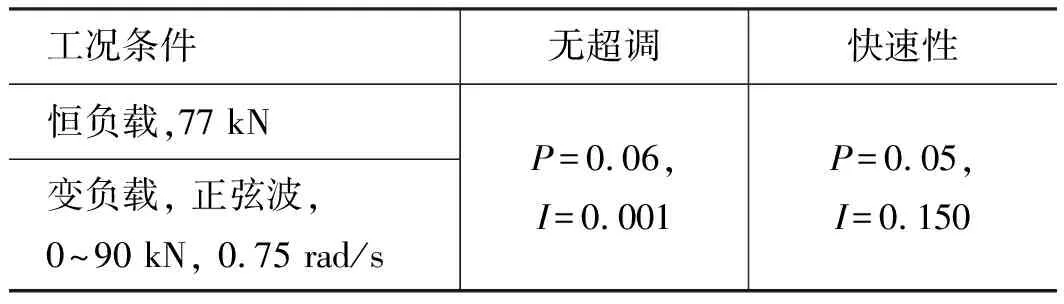
表5 兩種工況條件及PID參數

恒負載和變負載工況下預測控制和PID控制位置變化如圖8和圖10所示，對應控制電壓變化如圖9和圖11所示，穩態誤差如圖12和圖13所示。

從圖8和圖10中可以得出兩種工況下，穩態時真實位置均方誤差如表5所示。

從圖8～圖11可以得出，當采用PID控制時，為實現快速性，輸出必存在超調，控制值的變化會導致伺服閥不斷換向，為實現無超調，控制值雖平穩變化，但同樣需要一定的時間才到達穩態。從表4和表5中數據可知，同一組PID參數在變負載工況下，穩態輸出超調現象加劇，應對變負載工況存在局限性；為實現無超調響應，系統輸出會存在一定的穩態誤差，加強積分環節作用可提高系統位置輸出精度，提高快速性，但會產生超調現象。

圖8 恒負載工況活塞位移輸出曲線

圖9 恒負載工況控制器輸出電壓曲線

圖10 變負載工況活塞位移輸出曲線

圖11 變負載工況控制器輸出電壓曲線

表5 兩種工況真實位置均方誤差

采用模型預測控制可以實現在控制初期，輸出電壓信號迅速達到最大值，如圖9和圖11所示，在即將到達目標位置時，控制值逐漸減小為0 V，調試過程中，位置權重和控制權重的取值變化會影響該過程的動態效果；伺服閥始終單邊工作，避免了閥芯切換帶來的非線性，位置輸出如圖8和圖10所示，無超調現象發生；從表5可知，穩態時真實位置輸出均方誤差較小，從圖12和圖13可知，在恒負載和變負載工況下，穩態誤差均小于0.1 mm。因此，采用模型預測控制可以解決閥控非對稱缸系統固有特性和采用PID控制導致輸出超調和控制效果變差的問題，在不同工況下實現了快速、無超調、精確的位置控制。

圖12 恒負載工況活塞位移穩態誤差曲線

圖13 變負載工況活塞位移穩態誤差曲線

5 結論

(1) 高斯過程回歸實現了對混有噪聲數據的擬合處理，自適應獲取了超參數，得到了帶有置信區間的輸出結果。活塞預測位置增量的均方誤差較小，建立的離散數學模型精度較高。所需樣本數量少，縮短了單步預測時間。

(2) 提出了采用高斯過程回歸的閥控非對稱液壓缸模型預測控制方法，與PID控制相比，解決了為滿足快速性或負載發生變化時，輸出超調和控制效果變差的問題，實現了快速、無超調位置控制，定位精度滿足0.1 mm。