基于混合模型ad ap tive L ASSO方法的氣象數據實時變點檢測*

黃雄琪，田鎮滔，秦 睿，王雪梅，鄭陳亮

（廣西師范大學 數學與統計學院，廣西 桂林 541004）

1 研究意義及其背景

近年來，全球氣候變暖備受國內外學術界的關注。全球氣候的變化在近幾年的數據報告中呈現出致災性的特點，例如高溫、強風、強降雨這些極端天氣會促使自然災害的發生，繼而嚴重影響各國人民的生命財產安全。氣候變化所導致的一系列影響，讓全世界的學者們不得不重視氣象數據變點的分析及預測。

國內外有不少學者在研究變點問題。對于響應變量的個數比較少的情況，Horváth.L等[1]通過最小二乘的方法使用CUSUM方法檢測出了變點。Ga?briela[2]通過使用adaptive LASSO以及分位數的方法檢測出實時的變點。楊喜壽等[3]研究了氣候時間序列變點的推斷問題。Hawkins[4]研究了位置轉移替代方案的似然比檢驗，并應用于氣象數據序列的變點檢測。Buishand[5]討論了5種累積偏差檢驗的特點，使用累計偏差與平均值構建了檢驗統計量，并對荷蘭年平均氣溫進行了變點檢測。Alexandersson.H[6]等基于氣候時間序列，提出了一種在正態分布時間序列中檢測任意長度序列變點的新方法。Beaulieu.C[7]等考慮了氣候時間變化的復雜性和氣候數據序列的自相關性，提出了一種基于IA(informational ap?proach)的變點檢測模型。趙紅等[8]基于VFP環境，對氣象數據使用滑動t-檢驗法和Yamamoto法進行變點的檢測。許歡9]等運用ASAMC算法估計了氣象數據結構性變化的位置并給出了發生結構性變化的原因。

本文將降雨量作為被解釋變量Yi，將風向、風級等作為解釋變量X1,…,Xp，并且還考慮了被解釋變量的滯后性，引入變量Yi-1,…,Yi-k。通過Lasso方法找到了這幾個變量之間的關系，并且找出了降雨量對應的解釋變量的參數發生突變的時間點(變點)。

2 建立混合回歸模型

首先考慮簡單線性模型：

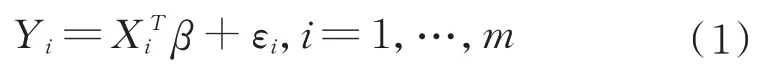
接下來結合解釋變量的滯后性，考慮如下模型：

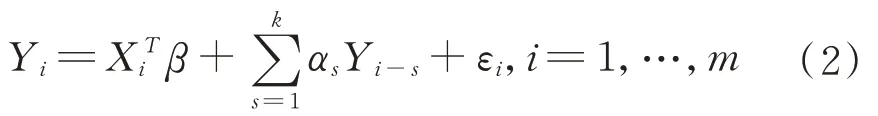
我們可以把(2)式轉化成如下模型：

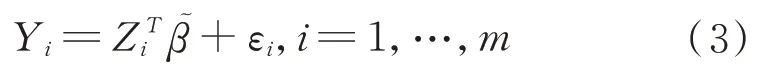
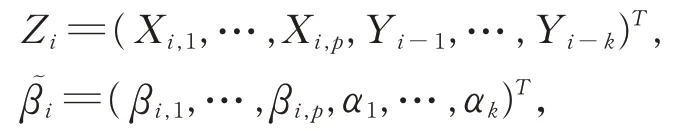
通過前m個觀測值得到簡單的最小二乘估計：

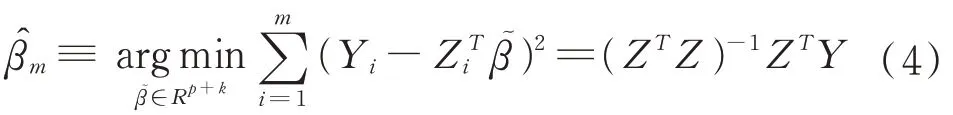
通過BIC準則可以篩選一些變量，但是篩選出來的變量不精確，借助LASSO可以解決變量的稀疏性問題，這個方法是1996年由Tibshirani.R提出的。在設計矩陣Z滿足某些且不使用假設檢驗的情況下，來消除掉一些不相關變量。之后在2006年zou提出了一種叫作的adaptive LASSO的方法，這個方法不需要設計矩陣Z的那些條件，方法如下：

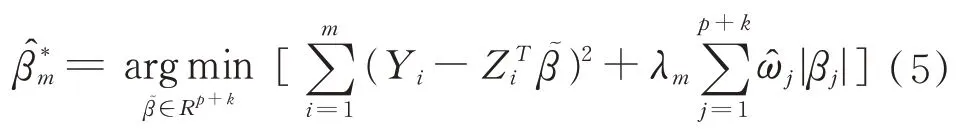
由此我們可以得到相應估計的殘差：

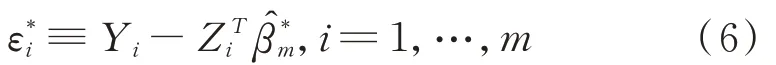
為了便于表述，引入指標集A≡{j∈{1,…,p+k};≠0}，同 理A*m≡{j∈{1,…,p+k};≠0}。其中A是真實參數的非零分量的指標組成的集合，A*m是使用adaptive LASSO估計得到參數的分量指標組成的集合。一般地對于參數?，我們用表示包含A相關因子的?的子向量。

考慮如下假設：

對于誤差εi：

（S1）ε1,…,εm,εm+1,…是獨立同分布的，E[ε1]=0，方差有限Var(ε1)＜∞，

（S2）對于解釋變量X1,…,X p,Y i-1,…,Y i-k存在一個正定矩陣C和常數η＞0，有，更進一步要求εi與Z i是獨立的。

在條件（S1）下Card(A)不依賴于m，設計矩陣m-1Z T Z收斂到一個正定矩陣C，調節參數λm有如下條件

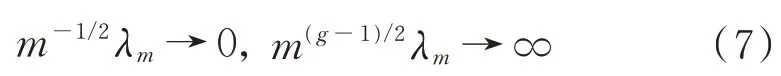
有adaptive LASSO估計值滿足oracle性質：

（P1）漸近正態性：

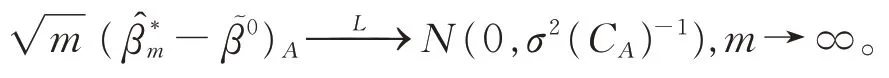
矩陣CA包含矩陣C對應的指標集A中的元素，對于β的最小二乘估計，可以得到

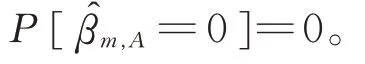
用上述方法得到β的估計后，我們可以得到總體方差σ2的估計：

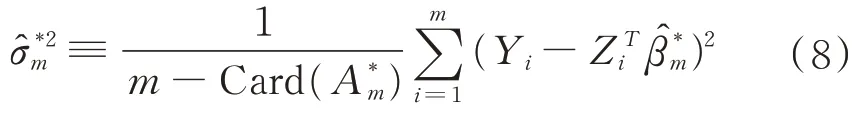
其中，Card(A*m)表示A*m的基數。

由于Card(A)不依賴于m，考慮adaptive LAS?SO的估計值的oracle性質，可以得到

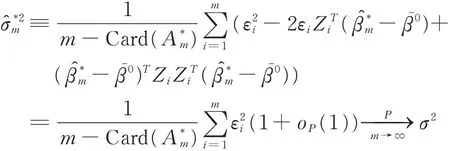
3 利用CUSUM方法構造檢驗統計量

首先考慮第一批m個觀測值之后的模型：

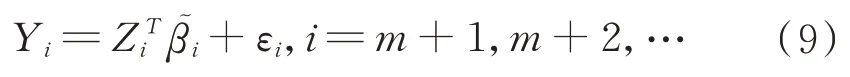
對于每一個給定的時間i，檢驗該模型的參數是否和第一批m個模型的參數一致:

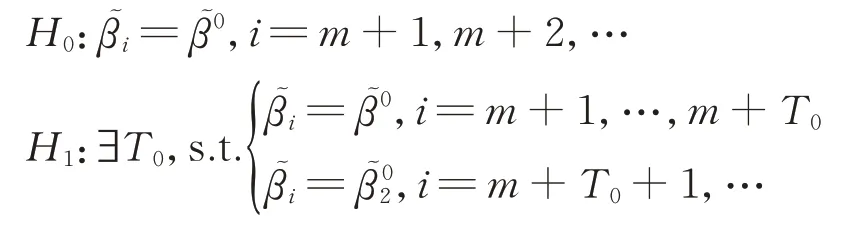
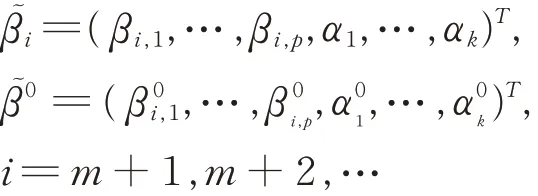
假設模型（2）是顯著的，即

為了構造統計量，將采用Horváth.L等的CU?SUM（cumulative sum）方法，在此之前先求出=Y i-,i=m+1,…,m+T，然 后 求的CU?SUM，即：對于某個T＞0,

對于給定常數γ∈[0,1/2)，考慮歸一化函數（此歸一化函數為有界函數）：

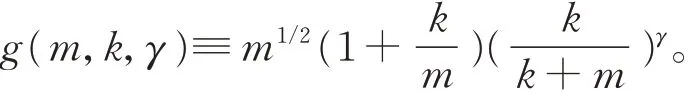
引理1在滿足假設（S1）（S2）的條件下，

（2）當備擇假設成立時，有

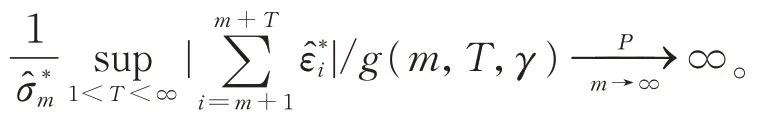
因此，根據上述假設檢驗可得到相應的檢驗統計量

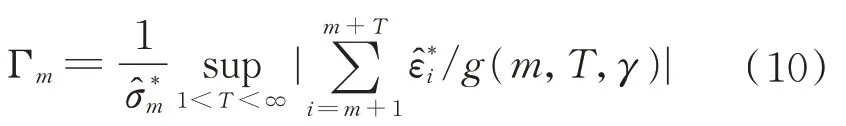
引理2對于給定的顯著性水平α容易通過模擬計算得到對應的分位點cα(γ)，因此，當原假設被拒絕時，可以得到停時：

4 桂林市降雨數據的變點估計

基于第二章提出的變點檢測模型，對廣西桂林市的降雨量真實數據進行實證分析。

氣象數據的預測問題是氣象學研究領域中公認的較為復雜的課題之一，其中降雨量為氣象數據預測中最難課題之一，降雨量大小引發的地質災害關系著人民生命財產安全，因此對降雨量大小的監控和精準預測是一項非常重要的工作。本文選取廣西桂林市的真實降雨量數據，基于第二章提出的變點檢測模型對降雨量的時間序列數據進行檢測分析，得出影響降雨量的因素以及降雨量的變點時刻，進而為相關氣象部門做好防護預警提供有力的依據，已達到減少人民生命財產損失的目的。

本章數據來自廣西桂林市2019年1月1日至2019年12月31日的降雨量情況。其中影響桂林市降雨量的變量如表1所示。

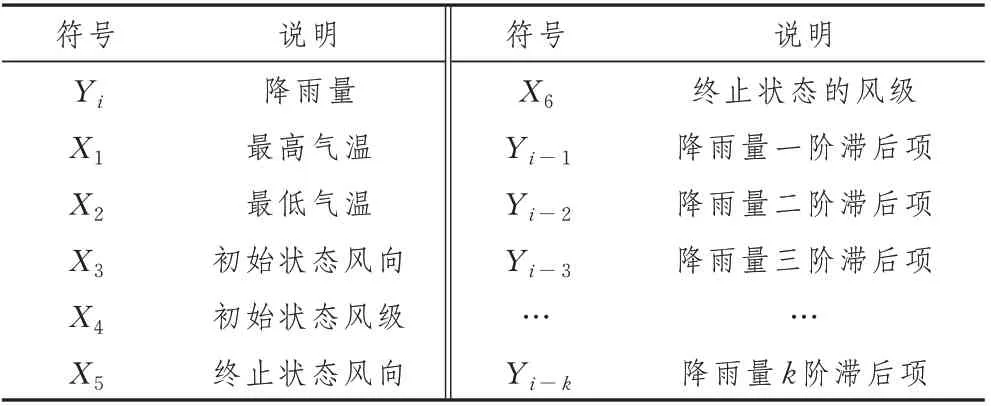
表1 桂林市降雨量的變量

圖1是桂林市降雨量情況的周度數據圖，可以看出時間在第23周時，降雨量發生驟變，容易看出這個數據是存在變點的，因此可以對桂林市降雨量數據進行變點檢測。

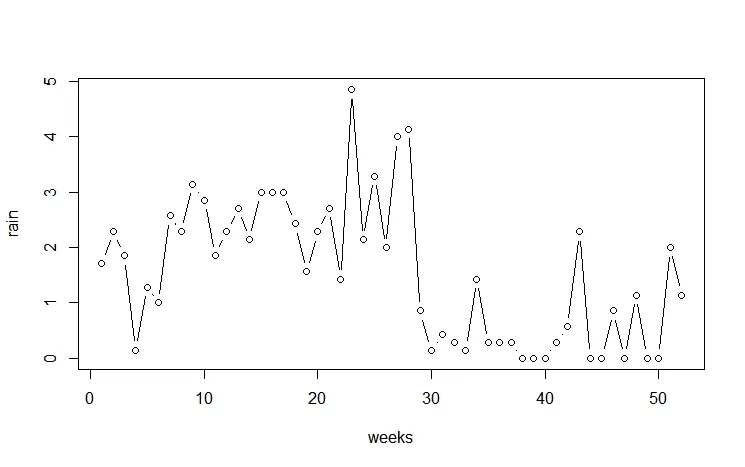
圖1 桂林市降雨量時序圖（周度數據）

首先研究降雨量數據的滯后情況。對數據進行時間序列分析，確定該降雨量序列是2階滯后的，因此確定滯后項階數k=2。

其次選用較簡單的最小二乘法(4)對降雨量數據進行分析，得到該模型(3)的最小二乘法估計為=(5.89,-0.34,0.06,0.025,-0.04,0,0,-0.21)T。

然后選用adaptive LASSO方法(5)對降雨量數據進行分析，得到該模型(3)的adaptive LASSO估計為=(4.66,-0.26,0,0,0,0,0,-0.06)T，再 根 據 得到adaptive LASSO估計易得總體標準差估計(8)為=0.73。

接下來根據數據模擬得到統計量的分位數為(γ=1 4,α=0.05)和cα(γ)=42.37645，并根據計算不同時間點統計量的值可以得到停時=83。

最后綜合上述分析和結果得出，只有最高氣溫和降雨量一階滯后項兩個解釋變量是影響廣西桂林市降雨量情況的因素，并得到桂林市2019年1月1日至2019年12月31日降雨量的變點在第m個數據后的第83個位置，按照實際時間計算得到變點時刻為2019年4月13日。換句話說，在4月中旬來臨之前，相關部門應該提前做好防洪防汛工作，防止內澇和次生災害的發生。桂林市在2017年和2020年分別發生了內澇，導致了政府和人民財產的損失。使用該方法對降雨量進行分析，可以為當地部門提供有效有力的數據支持和決策意見，以防止人員傷亡及財產損失。

2019年4月13日正值桂林市濕潤季風影響下的雨季，也是當地人俗稱的“南風天”。這說明本文建立的基于混合回歸模型adaptive LASSO方法較為準確的將實時降雨量驟變點檢測出來了，解決了一個氣象數據難預測的問題，進而得出該模型檢測效果不錯，能夠較為準確的定位降雨量變點，并且結果符合實際情況，具有較大的實際意義，也為后續研究其他氣象問題提供一種好用又準確的方法。