無失效數據場合威布爾分布失效概率的Bayes估計
曾 春,李云飛
(西華師范大學數學與信息學院,四川南充 637009)
0 引言
隨著社會的不斷進步,人們對產品的質量要求越來越高,在高可靠性產品的可靠性試驗中,往往沒有樣品失效,獲得的數據稱為無失效數據[1-2].威布爾分布是最常見的壽命分布之一,在應用概率統計和產品的可靠性分析中被廣泛應用[3],如何在無失效數據場合下,對壽命服從威布爾分布的產品的可靠性參數進行估計是值得深入研究的問題.
茆詩松和王玲玲[4]綜述了威布爾分布無失效數據的幾種處理方法,如經典方法、Bayes方法、最小χ2法、等效失效數方法;王玲玲和王炳興[5]利用修正似然函數方法對可靠性參數進行估計;倪中新和費鶴良[6]根據平均剩余壽命得到參數的擬矩估計,從而將無失效數據轉化為一個或多個失效數據的情形,最后利用分布函數曲線擬合方法得到未知參數的估計;張志華[7]將分布函數變換為凹函數,利用凹函數的性質對失效概率pi進行Bayes估計,進一步得到產品可靠性指標的估計;劉海濤[8]通過對分布函數進行變換,利用函數的凹凸性得到失效概率之間的關系,從而得到各時刻失效概率的估計;賈祥和王小林[9]在威布爾分布下,對配分布曲線法加以改進,使得計算結果不僅包含點估計,也包含置信區間估計;Erto和Guida[10]在形狀參數和特征壽命均未知的情形下,取形狀參數的先驗分布為均勻分布,固定時刻的可靠度的先驗分布為Beta分布,給出了可靠度的點估計和置信限;申珅[11]利用中位秩法在Excel中進行威布爾分布的參數估計的討論,從而獲得可靠性概率結論;李爽和李云飛[12]修正截尾時刻失效概率的取值上界,利用多層Bayes估計失效概率pi.
威布爾分布在產品壽命分析中扮演著重要的角色,其形狀參數的不同取值將產生不同的函數形態,不同的函數形態對應不同的產品失效階段和失效機理,所以按照威布爾分布形狀參數的不同取值對無失效數據進行估計是合理的[13-14].因此,本文考慮根據形狀參數m的不同取值范圍得到pi的取值范圍,并將關于pi的減函數(1-pi)2作為先驗分布的核,對pi進行估計,再利用加權最小二乘法估計可靠性參數.
1 模型假設
可靠性壽命試驗中的截尾試驗一般有定時截尾和定數截尾兩類,而無失效數據通常出現在定時截尾試驗中,所以本文將在定時截尾試驗下進行討論[9].
設產品壽命T服從威布爾分布Weibull(m,η),對應分布函數為
(1)
其中t>0,m>0,η>0,m為形狀參數,η為尺度參數.
隨機抽取S個樣品,分為n組,分別進行定時截尾試驗,對應截尾時間分別為ti(i=1,2,...,n),試驗樣品數分別為ni(i=1,2,...,n),所有樣品在試驗結束之前無一失效.則稱(ti,ni)(i=1,2,...,n)為無失效數據.
模型可做如下假設:
i)當t0=0時,產品的失效概率p0=P(T≤0)=F(0)=0;
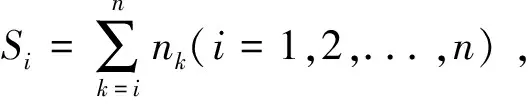
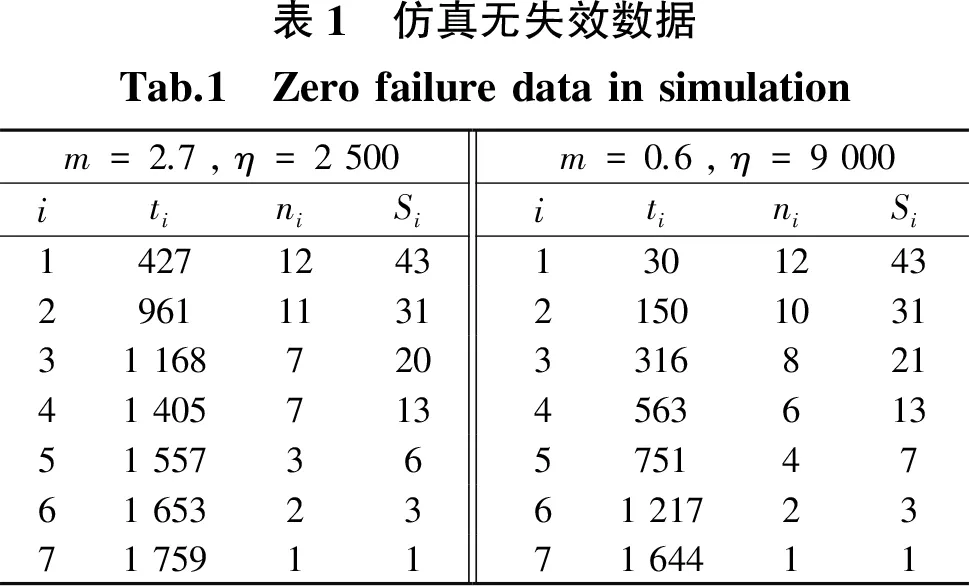
iii)0=t0 當m>1時, 文獻[14]中,將均勻分布作為pi的先驗分布,但是在無失效數據場合,失效概率pi大的可能性小,而小的可能性大,因此取勻分布作為pi的先驗分布不太合理.將關于pi的減函數(1-pi)2作為pi的先驗分布的核[16],此時滿足失效概率pi大的可能性小,而小的可能性大這一要求. 引理1[16]取pi的減函數(1-pi)2作為pi的先驗分布的核,則pi(i=2,3,…,n)的先驗分布為 證明由于在平方損失下,pi的Bayes估計即為后驗分布的期望,為此,先計算出pi的后驗分布,當 t=ti時,Si個產品均無失效,即失效數X=0,其似然函數為 L(X=0|pi)=(1-pi)Si. 根據引理1中pi(i=2,3,…,n)的先驗分布,pi(i=2,3,…,n)的似然函數以及Bayes定理,可得 pi(i=2,3,…,n)的后驗分布為 則在平方損失下,pi(i=2,3,…,n)的Bayes估計為: 所以F(t)是t的凸函數.根據凸函數的性質,當0=t0 由假設i),當t0=0時,p0=P(T≤0)=F(0)=0,所以 (2) 由假設iii)得0 Δpi2>Δpi1 (3) 類似定理1的證明.當形狀參數m=1時,威布爾分布即為指數分布,文獻[17-18]對其做了詳細研究. 在形狀參數m=2.7,尺度參數η=2 500和形狀參數m=0.6,尺度參數η=9 000時,生成兩組仿真無失效數據,按照文獻[19]的方法,將每組數據依次排序,分為7個小組,每個小組5個數據,將每個小組中最小的數據減1作為試驗截尾時間,可以認為,在此截尾時間內產品未失效.假設每組共有43個產品,每組試驗ni個產品,當t=ti時,有Si個產品未失效,從而得到兩組仿真無失效數據,如下表1所示. 當m>1時,利用文獻[14]提出的方法得到的誤差平方和為0.010 980 26,而本文提出得方法得到的誤差平方和為0.009 593 60;當 0 由于在無失效數據場合,失效概率大的可能性小,而小的可能性大,本文利用韓明提出的減函數法,將關于pi的減函數(1-pi)2作為pi的先驗分布的核,利用Bayes方法得到失效概率的估計,最后通過對仿真數據進行計算、分析、比較,驗證了本文提出的方法的合理性和可行性,同時通過比較誤差平方和,表明了本文提出的方法提高了失效概率的估計精度.2 形狀參數m>1下的統計分析
2.1 失效概率pi的取值范圍
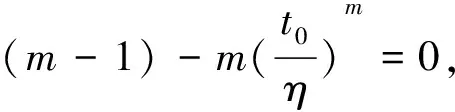




2.2 失效概率pi的估計

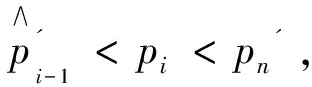
3 形狀參數0
3.1 失效概率pi(i=1,2,…,n)的取值范圍Ⅰ


3.2 失效概率pi(i=1,2,…,n)的取值范圍Ⅱ


3.3 取值范圍Ⅰ和取值范圍Ⅱ的比較

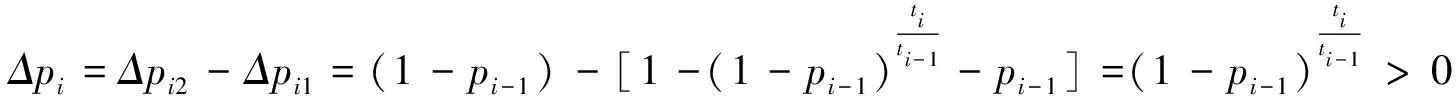
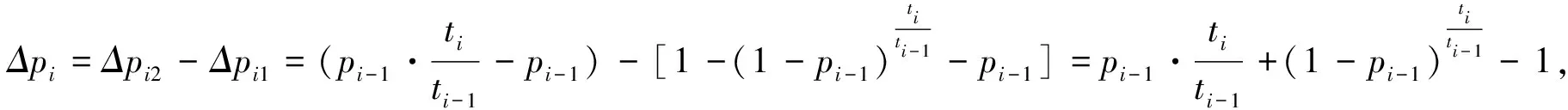


3.4 失效概率pi的估計
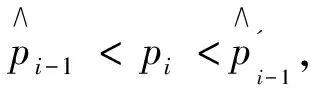
4 可靠性指標的估計



5 算例分析


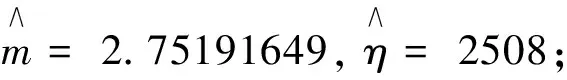
6 結論

