高中生數學解題中錯誤原因分析與教學策略探析

徐 麗

(安徽省廣德市第三中學 242200)

素質教育改革要求對學生的教學要以培養學生的學習能力、開發學生的思維為中心，特別是在高中數學課堂上，要重視對學生的解題能力的鍛煉，促進他們思維和創造力的培養.而在解題中，教學效果不夠理想，當前的教學模式比較單一和固定，在方式和手段上不夠科學，也不具有針對性，沒有對學生出現的錯誤類型和原因進行深入分析，導致很多學生在同一個問題上出現了多次問題，特別是一些基礎概念性問題成為了部分學生常常出現的錯誤，導致解題能力一直無法提升.因此教師要引導學生學會分析自己在解題過程中出現的問題，有針對性地培養解題思維.

一、高中生數學解題中出現的錯誤原因

1.運算能力差，出現計算失誤

高中數學學習中，對學生的思維能力要求較高，很多題目都需要實現思維的轉換，利用新舊知識的結合，將函數、幾何甚至是代數的知識融合起來，才能解決問題，這也就導致很多學生在解題的過程中，過于關注解題思路的發展和研究，長此以往，自己的計算能力也出現了問題，導致很多基本的計算概念知識逐漸遺忘，在實際解題的過程中，就容易出現各種計算錯誤.而很多高中數學題的解題過程是環環相扣的，如果出現了一次錯誤，會影響后續的運算過程全部出現問題，這就導致學生在解題的最后就會面臨無解以及解答錯誤的結果.而一旦出現了問題，學生可能由于思維定勢的原因會忽視計算問題，過多地關注自己的解題思路，對學生自信心的打擊比較大.

2.審題不清，忽視隱含條件

審題問題是很多高中生普遍存在的錯誤原因，而不同于小學和初中數學解題過程中出現的看錯條件、單位或者數字等低級錯誤，高中生犯得最多的錯誤是對題目的條件和結論等信息缺乏整理、推論和分析的能力，這就導致他們無法找到有用的條件，對于題目不同的形式以及內容背后隱藏的條件不理解，學生就無法找到快速有效的解題方案，導致解題過程比較復雜，思路繁瑣，學生的解題信心也會受到打擊.所以很多高中生沒有掌握審題的技巧，不能根據題目的條件進行深入分析和推導，給解題帶來更多的困難.

3.概念原理掌握不牢靠，運用時容易混淆

雖然高中數學題一般包含了不同類型的知識內容，解題思路也比較復雜，對學生思維能力和變通能力的要求比較高，但是歸根結底還是需要從基本的數學概念上進行延伸，了解數學理論的本質和內涵，才能達到熟練應用的效果.但是很多高中生在學習時眼高手低，忽視了對基本概念性質的學習和掌握，針對某些概念的運用方式和使用的范圍還模糊不清，不能夠分清不同概念之間的聯系和區別，運用時就會出現各種錯誤.而一旦基礎知識出現問題，解題時必然會困難重重.在選擇解題策略時，也會因為對概念不熟悉而無法選擇科學的方式進行解題.例如,已知函數y=1/2cos2x+√3/2sinxcosx+1,該函數的圖像可由y=sinx圖像經過怎樣的平移和伸縮變換得到.而很多學生在解題是對周期變換和相位變換的概念混淆，得出的答案自然也會偏離方向.

二、高中生數學解題教學的有效策略

1.加強概念性知識教學，提升基本運算能力

在高中數學解題學習中，基本的概念性知識是解題的鑰匙，也是學生必須掌握的，很多基本的定理在運用中可以發揮重要的作用.所以教師在新課教學中應該以培養學生扎實的基本功為目的，從不同的角度引導學生理解概念和性質，比如,集合的分類和性質，函數的定義，變量、自變量、因變量之間的關系，而這些基本的知識在后面各種函數知識的學習中發揮著重要的作用，是學生在解題中必須要引用和牢記的性質.其次計算仍然是基本功，而很多高中生會忽視基礎的計算訓練，基本的運算技巧掌握不牢靠.教師要對學生進行有目的地訓練，在平常的課堂教學中，有意識地引導學生進行計算訓練，可以從基本的概念著手，實現概念和計算同步教學，引導學生從概念入手訓練運算能力，提升學生的綜合實力.

2.重視理論和實際結合，提升分析能力

教師在教學中要引導學生去把握解題的思路，引導學生將理論和實際問題結合起來，理清自己的思維，有條不紊地對題目進行深入分析，從而找到正確的解題方向，逐步推演出解題的思路.其中，學生必須在審題之后，去分析出題的意圖和考察的知識點，根據自身的經驗，結合所學的知識，將可能應用到的理論都理出來，再通過深入探索，找到一些解題的路徑，不斷嘗試和排除，迅速找到最簡便快捷的解題方法.

例1 若不等式2x-1>m(x2-1)對于所有的-2≤m≤2都成立 ，則x的取值范圍是多少？

本題可以把m視為主變元，將原不等式化為m(x2-1)-(2x-1)<0,令f(m)=m(x2-1)-(2x-1)，再由題意得到f(-2)<0,f(2)<0,當-2≤m≤2時，f(m)<0恒成立，只需要滿足-2(x2-1)-2(2x-1)<0,2(x2-1)-2(2x-1)<0,即可解得x的取值范圍.

在上述例題中，分離參數時，會出現分離出參數與變量，所以需要進行思維角度的變換，實現“反客為主”，將習慣上的主元變與參數變量的地位進行變換，變個視角來重新審查恒成立的問題，從而可以實現對題目的降次和化簡的目的.因此在教學中，教師要根據實際問題和條件來進行解題，幫助學生實現思維的變換，才能掌握巧妙的解題技巧.

3.實施科學訓練，培養學生的數學思維

在解題過程中，學生的思維轉換能力尤為重要，學生不僅要掌握基本的解題方法，還要不斷提升自身的創造力，才能培養舉一反三的能力，在面對千變萬化的題目時，能夠挖掘題目中的有效信息，找到更多創新的解題思路，從而提升解題能力.首先，教師要對學生進行科學訓練，以質量為前提，摒棄傳統模式，讓學生能夠有更多的空間和時間去思考和反思.教師可以讓學生準備錯題集，定期對自己的錯題進行整理，發現自己易錯的知識點，才能更加準確地進行反思和鞏固，彌補自己的錯誤，不斷優化自身的知識體系，提高解題的質量.

例2已知a,b為正實數，2b+ab+a=30,求函數y=1/ab的最小值.

該題是一個二元函數的最值問題，教師可以先引導學生思考可以通過什么途徑進行解答，比如可以使用消元，轉化為一元函數問題；或者只用基本不等式的公式，考慮放縮后，通過解不等式的方式來解答.然后教師可以讓學生深入思考需要用到什么相關的公式，幫助學生理清思路，才能更好地提高解題能力.

4.巧用畫圖技巧，掌握科學解題方法

在高中數學解題中，畫圖作為一種重要的輔助方式，對提升學生的解題能力具有重要意義，而學生在解題中出現的思路不清晰、分析不到位等情況，都可以通過畫圖來實現對題目的分解，從而對具體的題目進行靈活變形.比如f(x)≥g(x)，就能夠非常容易畫出不等號兩邊函數的圖像，可以直接通過畫圖來得出結果，因此在選擇題和填空題的解題上，會更加方便和快捷.

例3求證：f(x)=(x+1-a)/(a-x),對于x∈[a+1,a+2]，該函數單調且恒有-2≤f(x)≤-3/2成立.

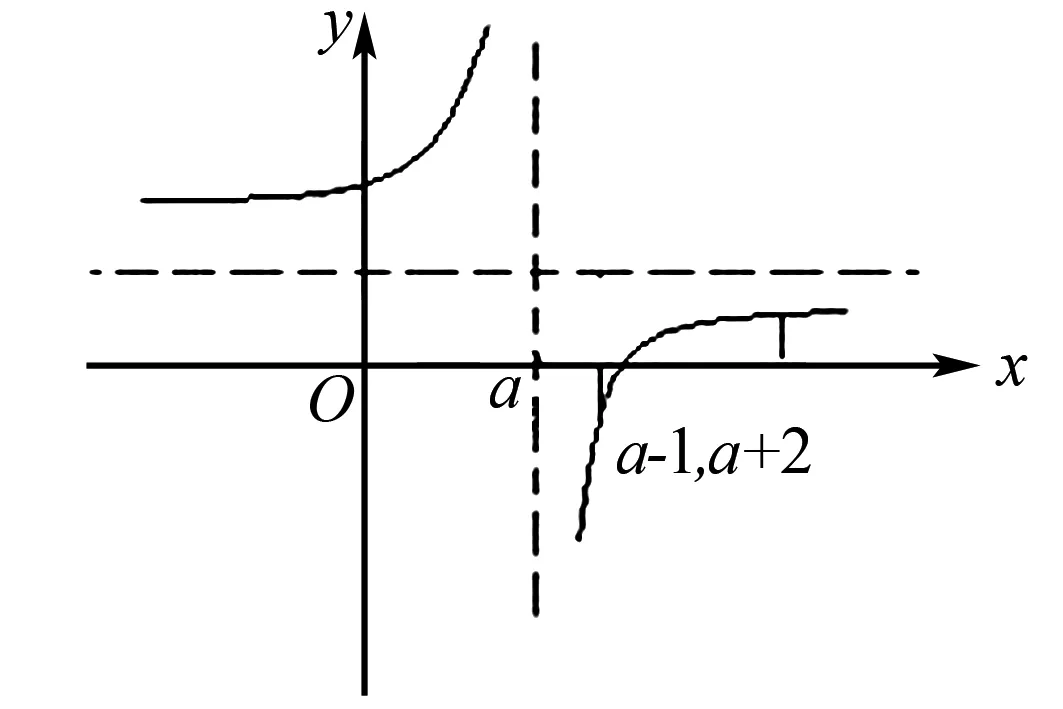
解析原方程可以化為y=1-1/(x-a),由圖像可知，x∈[a+1,a+2],該函數單調遞增，f(x)≤f(a+2)=1.5,f(x)≥f(a+1)=-2,所以可以得證.

綜上所述，在高中數學課堂上，學生在解題中容易出現各種錯誤，面對學生出現的各種問題以及教學中的各種阻礙因素，教師應該保持耐心，深入分析原因，找到問題所在，再結合不同學生的問題來優化教學和指導方式，根據不等式知識的特點科學教學，重視對學生審題意識、創造能力以及思維方式的培養，幫助其掌握正確的解題思路，提高學生整體的解題能力.