一題多變 提升數學思維深刻性

周 沖

(江蘇省南通市通州灣三余初級中學 226331)

初中數學培養學生探究性思維和發散性思維，提倡一題多變的形式.要求學生做數學題時，能及時聯想知識之間的關聯性，靈活解決不同的問題，實現多解歸一.一題多變，就是對同一道問題多次改變條件或者結論，再進行思考并解答.初中數學教學要應用一題多變模式，培養學生舉一反三和觸類旁通的能力，提升數學思維的深刻性和靈活性.筆者結合實際教學經驗，提出橫向聯想、縱向變式和綜合轉化三種模式，以達到訓練學生數學思維的目的.

一、橫向聯想，改變外延

橫向聯想，要求學生在學習過程中打破思維局限，以知識之間的橫向相似為出發點，提出新的想法和觀點.橫向聯想要求學生不僅掌握書本知識，還懂得了基本的計算規則和方法，在知識外延的拓展訓練中，深刻理解了相關理論的用法.學生從知識的橫向聯系中獲得啟發，從而發現知識或者方法的開放性，同時也理解了解決問題的靈活性.

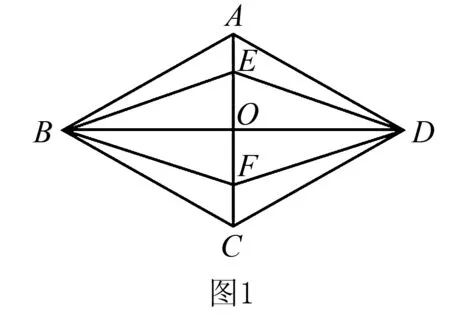
例如，“菱形”的教學中，菱形的性質有兩個：(1)四條邊長度相等；(2)對角線互相垂直且平分.事實上，基于這兩個性質，會發現菱形的判定方法有兩個：(1)4條邊長度相等的四邊形為菱形；(2)對角線相互垂直且平分的四邊形為菱形.因此，菱形的性質與判定方法互為橫向關系.為了讓學生更好地理解這種關系，筆者設計了一道例題，如下圖1所示：已知四邊形ABCD為菱形，其對角線AC和BD相交于O點，在OA和OC上分別取一點E和F，使AE=CF，試分別基于菱形兩個性質和判定方法證明：四邊形EBFD為菱形.針對此題，學生首先可以用需要用正向思路利用菱形四邊相等性質及三角形全等定理證明EB=BF=CF=FD.其次，可以利用對角線垂直平分性質證明OE=OF，進而再基于菱形對角線垂直平分判定方法證明四邊形EBFD為菱形.由此，同一道題通過證明方法的橫向變遷，學生就會菱形性質及判定方法的橫向互換，通過對比還會發現兩種證明方法哪個更快，提升遷移能力.

所以，橫向聯想能夠活躍學生的思維，讓學生在解題過程中不再生搬硬套，而做到靈活創新.但橫向數學思維模式的培養，需要有一定的“似曾相識”度，要求學生有一定的解題經驗，才能在面對相似問題的時候，采取構造、轉化或者遷移的方法解決問題.在橫向一題多解的過程中，重組了學生零散的知識，也充分調動了他們思維能力，磨練了意志.

二、縱向變式，深處漫溯

橫向主要是通過一題多變或者一題多解讓學生的思維更加開闊，而縱向變式則主要提升學生對復雜情況或未知問題，積極思考聯系已有知識并加以應用，提升對已有知識的深度應用，進而實現深度思維的提升.初中數學的知識點相對較多，聯系也錯綜復雜，因而，非常適用于采用縱向變式提升學生的深度思維能力.

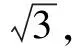
(x+1)t2+(2x2+x)t+x3=0

(1)

再對上式(1)進行因式分解，注意，化簡后的方程式關于t的一元二次方程，而不再是關于x的一元三次方程，意味著x是個未知常量.分解后的因式為：

(t+x)[(x+1)t+x2]=0

(2)

解答上式(2)得到x+t=0或者(x+1)t+x2=0

學生根據二次方程根的形式繼續解題，獲得最終答案.數學算式解答，需要學生摒棄思維定勢，具備一定的深度轉換思想，已知未知轉換、有理無理轉換、數和式統一、函數和形結合，才能利用已知的公式進行創新突破學習，拓展思維，獲得知識的外延.

縱向變式是一種有效提升學生探索意識的方法，在實際教學中，教師需要適時地開展縱向變式的引導教學，讓學生不再局限于基礎知識，而是基于基礎進行深度探索求知，讓思維活躍的同時，提升縱向探究能力.

三、綜合轉化，發現規律

創新既需要橫向拓展，也需要縱向探究.初中數學中一題多變的目的是為了提升學生數學綜合思維能力，進而培養綜合素養.讓學生從多角度、多方位和多層次對數學問題進行思考，其目的是樹立學生面對問題有突破思維局限的意識，更深刻地理解自身所學的數學知識，將“不變”的知識通過橫、縱向搭配，探究“變”的問題和規律.

例如，圖2所示的圖形，求證：∠A+∠B=∠C+∠D.這個題目很簡單，學生既可以用三角形內角和為180°與對角相等搭結合來證明，也可以直接用三角形的外角性質(任意一個外角等于與它不相鄰的任意兩個內角之和)與對角相等結合來證明.但如果遇到圖3所示的情況，求證：∠A+∠B+∠C+∠D+∠E=180°.其僅僅橫向遷移就很難解題了.解決這個問題，需要學生將三角形內角和為180°向多邊形的內角和為(n-2)×180°縱向拓展，才能再基于三角形內角和進行求解.首先，需要學生對圖形進行觀察，思考怎樣搭建這五個角的等量關系.其次，學生首先會嘗試利用小三角形，如△AFJ，基于此擴展范圍至大三角形，如三角形ACI，可以建立∠A+∠C+∠AIC=180°.以此類推，發現內部五邊形每個角都用了一次三角形內角和等式，而∠A、∠B、∠C、∠D和∠E重復運用了兩次，因此，(∠A+∠B+∠C+∠D+∠E)×2+(∠AIC+∠EFC+∠AGD+∠BHE+∠BJD)=5×180°=900°.再結合五邊形內角和，進而進行計算就可以得出：∠A+∠B+∠C+∠D+∠E=180°.由此，學生就會樹立起三角形性質和多邊形內角和之間的橫縱向聯系，提升幾何解題思維.

綜合轉化對于初中教學是一大難點，在實際教學中，不能完全以試題答案為主線引導學生思考，而應該基于客觀，進行必要的試錯反思，樹立正確的解題規律意識，才能培養學生正確的綜合轉化思維.

綜上所述，一題多變的數學學習方法，可以讓學生快速識別并抓住問題核心，找到問題本質和規律，快速計算出結果.這種學習方式，使得學生思維得到了拓展和遷移，培養了學生的邏輯思維.當然，一題多變的方式不僅限于上述三種，不管什么樣的變化方式，終究脫離不開書本的相關定義、定理、公式等，所以在培養學生變化思維的過程中，應當注意以不變應萬變的思考方式，不能為了追求“變”而忽略“不變”.