新型搓澡與按摩機器人的動力學控制研究

張浩強，蔡 柳，盧森幸，林彥伯

(河池學院，廣西 宜州 546300)

0 引言

近些年來，由于并聯機構集合了其他機構高剛度、高承載力和高精度的特點，使其進入了國內外很多研究機構的視野，并廣泛應用于野外探索和礦井采樣勘探領域[1-4]。

在并聯機構的應用領域中，國內學者郝亮亮等[5]首先從3-RPRS并聯機構的運動學求解及仿真入手，驗證其在跳躍機器人中的應用。文獻[6-8]分別將并聯機構應用于機構的協同避障、殘余振動抑制、提高手機攝像頭的裝配精度等。從以上研究可以肯定并聯機構的關鍵點在于精度的控制，為了提高并聯機構對預設軌跡的追蹤精度，研究人員對多種控制方法展開了研究。文獻[9-14]成功建立了并聯機構的動力學模型，在此基礎上運用模糊PID控制，實現了高精度、快速響應的性能提升。文獻[15-16]分別在對3-CP_aRR和3-RPS并聯機構的動力學分析基礎上進行了實時控制系統的控制研究。

本文以六自由度3T3R對稱新型3-RPRS并聯機構為對象展開研究,設計了其動力學控制方法。

1 3-RPRS并聯機構構型分析

新型搓澡與按摩機器人利用了并聯機構的優點，其基本構型為3-RPRS并聯機構，由基礎平臺(半徑為R的共面圓B1B2B3)、運動平臺(半徑為r的共面圓S1S2S3)及3條RiPiRiSi(i=1,2,3)對稱支鏈組成，機構簡圖如圖1所示。3-RPRS并聯機器人RiSi連桿長為li，豎直滑塊滑動距離為Pi，即為并聯機器人各構件間的鏈接關系。

圖1 3-RPRS并聯機構簡圖

根據3-RPRS并聯機構的幾何約束關系，分別在基礎平臺和運動平臺幾何中心建立全局坐標系(定坐標系)B-XYZ和動坐標系p-xyz。設動平臺幾何中心點p的全局坐標為p(xp,yp,zp)，滑桿Pi與基礎平臺水平面的夾角為θi，連桿RiSi與水平面間的夾角為φi。由幾何關系，考慮到3-RPRS并聯機構支鏈對稱，本文簡化為一條支鏈進行分析。

利用修正的G-K公式[17]對該并聯機構進行自由度的計算，即：

(1)

其中：d為機構的階數，d=6；n為包括機架的桿件數目，n=11；N為運動副的數目，N=12；fi為第i個運動副的自由度數；v為并聯冗余約束數，v=0；ξ為局部自由度，ξ=0。

將相關數值代入式(1)計算得：M=6。故新型并聯機構可以實現6自由度空間3T3R的運動，這表明機構運動平臺末端輸出運動不受限。

根據機構的幾何關系，求得點Si在全局坐標系下的坐標:

S1=(0,R-P1cosθ1-l1cosφ1,P1sinθ1+l1sinφ1).

(2)

(3)

(4)

而對于搓澡與按摩3-RPRS并聯機器人來講，機構的動坐標系p-xyz相對于全局坐標系B-XYZ的旋轉矩陣可表示為：

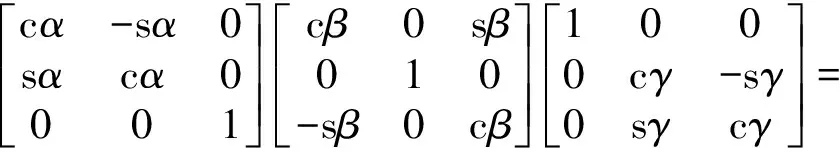
(5)

其中：TZ,α、TY,β、TX,γ分別為繞Z軸、Y軸和X軸的旋轉矩陣；α、β、γ為歐拉角；s與c分別為sin和cos。

當給出3個歐拉角α、β、γ時，動坐標最終的姿態矩陣Tp就可以確定，那么在動坐標系中的任一向量SiT可以通過坐標變換方法變換到定坐標系中，故有：

(6)

其中：p為動平臺幾何中心點處位置矢量，其在定坐標系中為p=(xpypzp)T。

同理，可推導出點Si在動坐標系下的坐標:

(7)

由式(2)～式(7)聯立可以得到搓澡與按摩3-RPRS并聯機器人的位置解。

2 逆動力學模型求解

采用虛功原理來研究機構的逆動力學求解問題，由虛功原理可得機構整體的動能方程為：

(8)

(9)

將式(9)對時間求導得：

(10)

將式(8)對廣義坐標變量q求導可得：

(11)

則支鏈的勢能函數為：

Ep=gTJ(q-q0).

(12)

其中：g為支鏈重力；q0和q分別為動平臺的初始與當前位姿矩陣。

將式(12)對廣義坐標變量q求導，則有：

(13)

由以上分析可得并聯機構的廣義力為：

(14)

廣義力F是機構動平臺位姿變化伴隨產生相應的“驅動力”。根據虛位移原理可知，3-RPRS并聯機構的外力為關節驅動力和動平臺所受外載荷，故其所做的虛功為：

(15)

其中：Fw為機構所承受的外載荷；δq為機構的廣義虛位移；fD為機構支鏈的驅動力。

根據虛功原理，可以得到并聯機構的廣義驅動力所做的虛功為：

W2=fDJTδq+FwGTδq.

(16)

由式(15)和式(16)聯立求解得到：

fD=J-T(F-GTFw).

(17)

對于新型搓澡與按摩機器人來講，求解其動力學逆解方程，即是已知動平臺的運動軌跡，求解驅動關節輸入力的問題。

3 并聯機構控制系統的控制策略

數學工具Simulink在運動控制方面仿真效率高、邏輯結構準確清晰且非常適合動態系統的建模與分析，故本文根據機構的構型特點，在Simulink中添加各運動副、相應剛體Body及傳感器建立并聯機構的結構模型和系統框圖，如圖2、圖3所示。

圖2 3-RPRS并聯機構結構模型

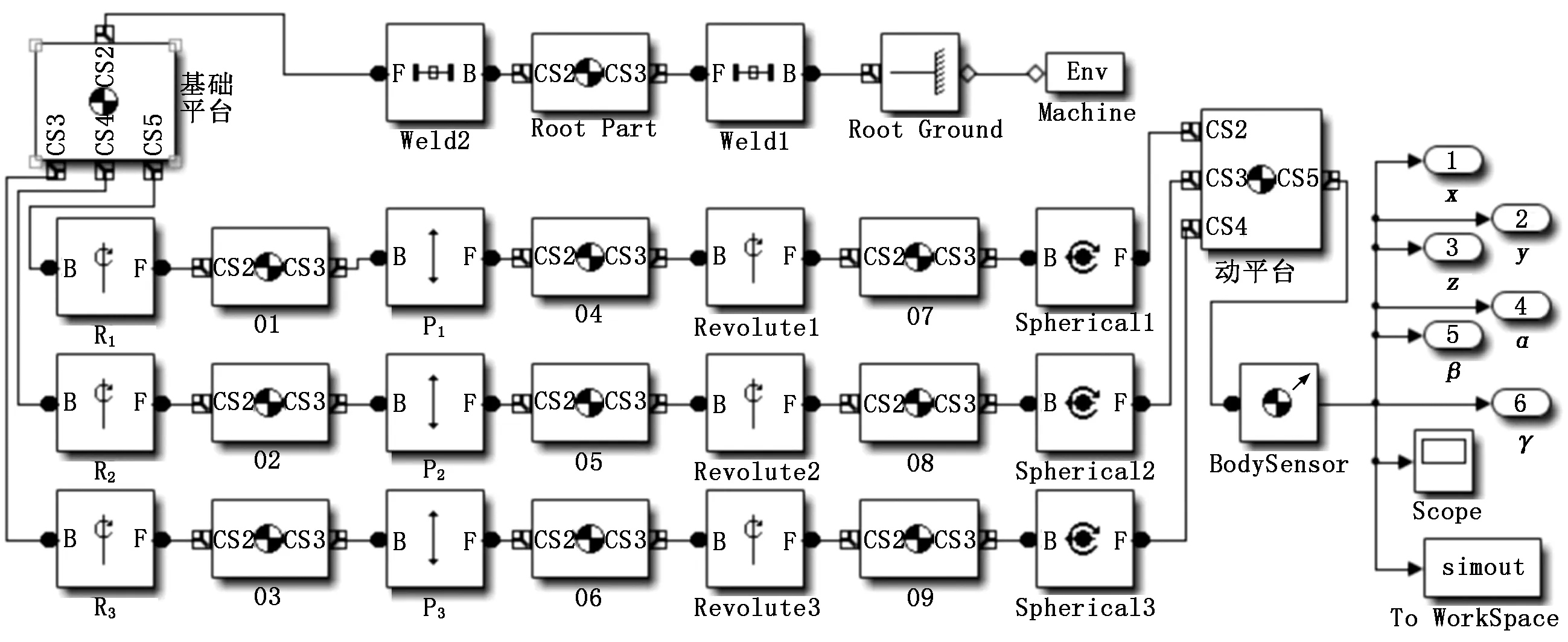
圖3 3-RPRS并聯機構系統結構框圖

并聯機構的動力學特性隨著其運轉速度的提高而明顯增強，且呈現非線性的變化規律。為了保證并聯機構的動態位置控制精度，因此本文引入基于動力學模型的前饋控制[18]的改進控制方法。改進后的控制方法是以整個機構的系統結構為控制對象，通過逆動力學模型求解，從而得到動力學前饋控制信號，并通過補償算法反饋到閉環控制系統中。并聯機構動力學前饋控制系統框圖如圖4所示。

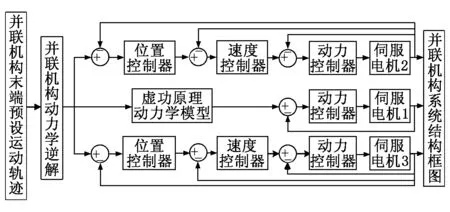
圖4 并聯機構動力學前饋控制系統框圖

4 并聯機構系統算例仿真

假設給定3-RPRS并聯機構實驗平臺的額定外載和約束條件以及末端預設運動軌跡，通過機構的動力學方程以及所構建的Simulink逆動力學系統結構框圖，結合并聯機構動力學前饋控制系統對其動力學進行仿真。為進一步驗證控制系統的有效性及精度控制性能，在此基礎上聯合ADAMS虛擬樣機對并聯機構進行虛擬仿真驗證。本文采用文獻[5]中的3-RPRS并聯機構參數來進行仿真，機構初始位姿參數值參考設定如表1所示。

表1 機構初始位姿參數值參考設定

設定預設軌跡包含兩組：一組為簡單預設軌跡；一組為復雜預設軌跡。依據符合一般性原則及系統物理參數模型，在并聯機構動力學前饋控制系統中對并聯機構進行算例仿真，仿真得到的結果如圖5～圖11所示。

從圖5和圖8來看，3-RPRS并聯機構前饋控制系統下的修正理論系統動力學模型軌跡與實際軌跡存在偏差，但修正后的實際偏差較小，運動方向穩定，體現出控制的有效性。

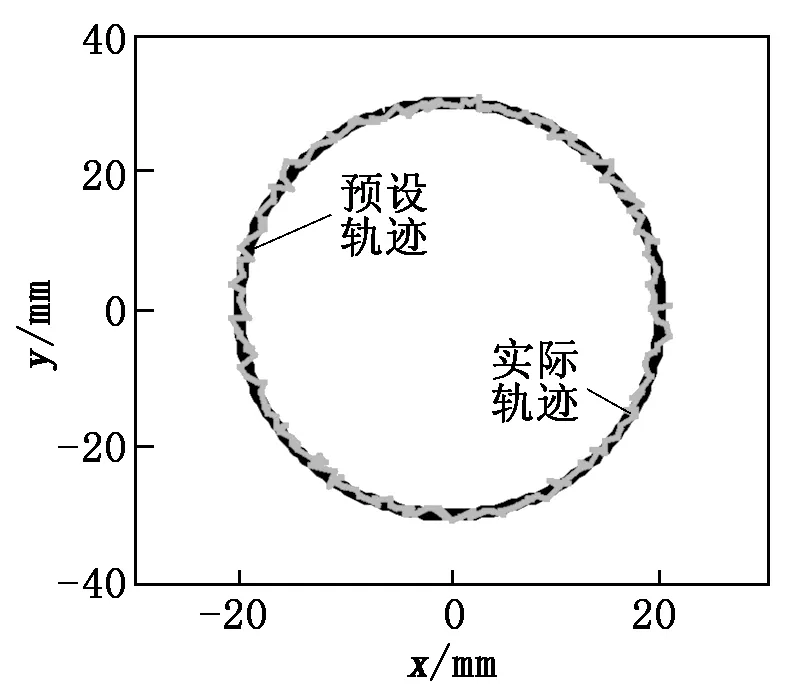
圖5 簡單預設跟蹤軌跡

從圖6、圖7和圖9～圖11來看，3-RPRS并聯機構前饋控制系統下的修正理論系統動力學模型與實際軌跡存在的各向位移偏差變化在±1 mm以內，80%的位移偏差控制在±0.8 mm以內；從機構前饋控制系統在簡單軌跡和復雜軌跡追蹤結果來看，簡單軌跡更具波動性而且波動次數也更多，這也驗證了前饋控制系統對復雜預設軌跡的追蹤效果更好，能夠較好地減少追蹤過程產生的誤差。仿真結果表明，前饋控制系統可以對3-RPRS并聯機構的運動軌跡進行較為準確的控制，而且控制過程較為平穩。

圖6 簡單預設跟蹤軌跡在x方向上的誤差圖7 簡單預設跟蹤軌跡在y方向上的誤差圖8 復雜預設跟蹤軌跡

圖9 復雜預設跟蹤軌跡在x方向上的誤差圖10 復雜預設跟蹤軌跡在y方向上的誤差 圖11 復雜預設跟蹤軌跡在z方向上的誤差

5 結語

本文對新型搓澡與按摩機器人構型展開動力學研究，研究結果表明：

(1) 利用修正的G-K公式分析得到并聯機構的自由度為6，建立該機構的加速度和速度的映射關系；利用虛功原理推導了Lagrange逆動力學方程，求解了驅動力。

(2) 在此基礎之上，建立并聯機構的結構模型和系統框圖，以此引入基于動力學模型的前饋控制的改進控制方法和前饋控制系統。

(3) 算例仿真驗證了理論推導的有效性，該機構的運動情況穩定、無突變；3-RPRS并聯機構前饋控制系統下的修正理論系統動力學模型與實際軌跡存在的各向位移偏差變化在±1 mm以內，80%的位移偏差控制在±0.8 mm以內，可以保證并聯機構運動穩定性，體現出動力學控制方法的有效性。

此控制方法不但能有效地提高機構位置控制精度，而且可以發揮機構運動學閉環控制抗擾動能力強的特點，降低單純的前饋控制算法對機器人系統動力學模型高精度的要求。