基于機器學習的高應力軟巖巷道支護抗毀能力預測

鄧廣哲，付英凱

（1.西安科技大學 能源學院，陜西 西安 710054；2.西安科技大學 西部礦井開采及災害防治教育部重點實驗室，陜西 西安 710054）

高應力軟巖巷道支護抗毀能力始終是煤礦開采過程中核心問題，在煤礦開采時，經常出現溫度逐漸升高，地應力逐漸變大或者地質逐漸發生惡化的情況，這些問題常常導致軟巖巷道發生開裂、鼓包或者變形的問題[1-5]。高應力軟巖巷道支護在世界范圍來看，屬于較為復雜的工程建設問題，對于煤礦資源開采是具有重要意義的。隨著開采深度的加大，高應力軟巖巷道支護問題嚴重突出，解決當前高應力軟巖巷道支護問題，是煤炭開采過程中安全生產關注熱點之一[6-8]。

目前，國內外許多學者對該問題展開了研究，余偉健等[9]針對薄煤層變形特征提出了“錨、網、索、梁”整體支護技術；王衛軍等[10]提出了可接長錨桿技術對大變形巷道進行支護取得了較好的效果；黃慶享等[11]采用物理和數值模擬分析了軟巖大變形巷道變形情況，提出了全斷面錨桿索+梁噴漿支護；雖然上述方法取得一定的進展，但是對于復雜巖層，應用能力不足，圍巖巖層基本為軟巖，且巷道斷面大、布置密集、強度低。隨著礦山開采速度加快，深部高應力軟巖巷道支護初期來壓較快，巷道支護自穩能力較差，如果不加速控制很快就會出現巷道支護毀壞。而通過對軟巖巷道支護效果進行預測將對圍巖控制提供借鑒，劉學生等[12]采用遞進預測和非遞進預測方法對巷道兩幫移近速度進行預測，馬鑫民等[13]研發了工程類比煤巷支護智能預測系統，王宏偉等[14]采用神經網絡方法對巷道變形進行了預測。但以上方法多依靠工程經驗，為此，從圍巖強度特性、圍巖屬性及流變特性等方面分析了軟巖巷道支護失效機制，針對采用基于語義特征、深度學習、特征融合方法存在數據分布差異性的問題，提出了基于機器學習的高應力軟巖巷道支護抗毀能力預測方法；從現有高應力軟巖巷道數據中遷移知識，幫助高應力軟巖巷道將來學習，并在自然環境中應用機器學習模型訓練相關數據[15-20]，在這些情況下，遷移數據學習能夠幫助預測研究提供全新場景，使機器學習在無大量標簽數據環境下進行預測。

1 高應力軟巖巷道特性分析

1.1 強度特性

因為軟巖巷道存在圍巖自身高應力的特點和圍場低強度的性質，在此基礎上，增加了軟巖巷道支護措施的難度。因此開展巖石力學性質試驗與分析，為高應力軟巖巷道支護的穩定性提供依據。在巖石力學性質試驗中，選擇完整塊度大的高應力軟巖巖塊，從巖塊中取出巖心來進行物理力學性質的試驗，巖石物理力學性質見表1。

表1 巖石物理力學性質Table 1 Physical and mechanical properties of rock

由于泥巖中含有多種膨脹性黏土和礦物質，當礦泥巖與水發生混合時，泥巖承載力降低或消失，極易引發泥化、崩解的危害。因此巷道在開挖后采取封閉圍巖的保護措施，尤其是對于后期失穩變形的巷道圍巖，重點加強對圍巖的保護。如果保護措施不當，在施工中通風、用水作業環境下，巷道圍巖就會出現吸水現象，此時引發圍巖體膨脹。而在失水狀態下會發生巖體收縮現象，造成巷道圍巖強度和完整度快速降低，加劇巷道圍巖的變形和損壞[21-23]。

1.2 支護構件模型

利用FLAC3D軟件建立起模擬尺寸，對模型底部位移進行約束。建模時不需要區分圍巖的巖性，也不需考慮巖體的自重，只是將巖層水平簡化處理，同時對圍巖材料參數等效均質化處理。假定圍巖三向的應力值均一樣，采用六面體單元，支護構件模型如圖1。

圖1 支護構件模型Fig.1 Support component model

通過建立支護構件模型，設計與現場巷道條件一致計算模型，模型內等間距布置錨索、噴層、拱架、等間距布置錨桿，驗證現場圍巖變形破壞情況。

2 高應力軟巖巷道支護階段時間確定

軟巖巷道在施工時，極易發生大變形失穩的現象，根據是由于以下特性導致的：①軟巖的本質特征，當含有膨脹性礦物的泥質巖類在低應力水平的施工中，就產生了非線性、非光滑的顯著塑性變形的現象；②構造、埋深和采動引起的高應力作用于軟巖巷道，引起圍巖的擴容變形以及圍巖劣化。但不管造成軟巖巷道大變形原因如何，當軟巖巷道發生變形或者膨脹的變化時，各變形或膨脹區域的應變曲線是相對的。彈性區在最外圍，塑性流動區在最內圍。塑性硬化區和塑性軟化區分布在中間層，軟巖巷道變形區具體分布如圖2。

圖2 軟巖巷道變形區分布Fig.2 Distribution of deformation zone of rock roadway

根據圖2中可知，變形速度會隨著煤礦巷道開挖進展發生相應變化，其中共分為3個階段，分別是減速變形階段、近似線性恒速變形階段和加速發展變形階段，若接近最后加速發展變形階段，巷道巖體結構就會發生巨大改變，巖體出現新的裂紋，導致其強度減弱。由于軟巖巷道與硬巖巷道的本構關系，因此應采取不同支護措施。軟巖巷道可以將塑性能以某種形式釋放出來，因此軟巖巷道支護原理可以表示為：

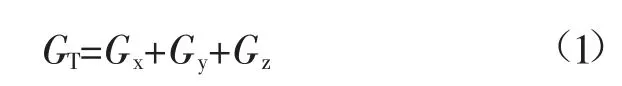
式中：GT為軟巖周圍巖層向臨空區域運動的合力；Gx為彈塑性轉化的工程力；Gy為軟巖自撐起力；Gz為工程支護力。

在加速變形階段，使彈塑性轉化的工程力達到最大，但卻大大降低了軟巖自撐起力，并不滿足優化準則，因此，需確定最佳支護時間。最佳支護時間是指在各個交互點所需的最佳時間，最佳支護時間如圖3。

由圖3可知，（G1+G0）-t表示曲線峰值點所對應的時間t1時既為最佳支護時間。通過分析可知，該點與其他曲線G0-t和G1-t交互所需支護時間相似。

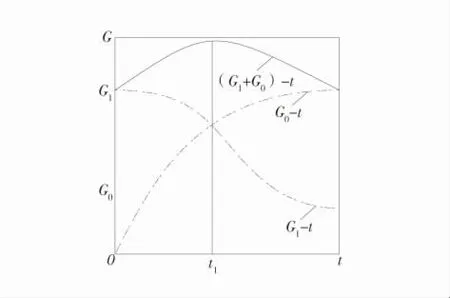
圖3 最佳支護時間Fig.3 Optimal support time

3 支護抗毀能力預測方案實現

機器學習是在高應力軟巖巷道支護抗毀能力預測任務以性能度量衡量的性能，隨著經驗自我完善，通過學習歸納和總結，重新組織已有的學習結構，進而不斷完善改善自身性能。通過學習進行歸納、總結，將機器學習技術應用到預測之中，可大大減少資金投入，使用機器學習方法預測高應力軟巖巷道支護抗毀能力。

3.1 高應力軟巖巷道支護參數求解

將高應力軟巖巷道支護結構簡化，簡化后的模型可在軟巖巷道支護上起到保護作用。若設軟巖巷道支護邊緣節點在檢測時受到破壞，其水平方向的受力就會發生實質性變化，同時位置發生改變。高應力軟巖巷道支護彈性變化過程存在如下關系：

式中：［W］、［W′］、［W″］分別為高應力軟巖巷道支護結構質量參數矩陣、高應力軟巖巷道支護結構阻尼矩陣、高應力軟巖巷道支護結構層間恢復力向量參數矩陣；α¨、α˙為高應力軟巖巷道支護結構位移變化機關向量；α為高應力軟巖巷道支護結構層間恢復力向量；β為外界作用力。

［W］可表示為：

式中：Wn為第n層高應力軟巖巷道支護結構的集中質量值；［Wc］為結構質量矩陣。

高應力軟巖巷道支護結構僅需要考慮支護結構的外界破壞動力作用，同時忽略其余支護受力位移。采用數值積分法，獲取高應力軟巖巷道支護結構受到破壞的加速度和位移，由此獲取高應力軟巖巷道支護在破壞性外力作用下高應力軟巖巷道支護受損情況。構建強破壞力作用下的高應力軟巖巷道支護抗毀能力預測模型，精準分析結構抗毀性。

3.2 預測模型設計

設計強破壞力作用下高應力軟巖巷道支護抗毀能力預測模型前，需對高應力軟巖巷道支護加固。在中強度破壞力作用下，原始高應力軟巖巷道支護加固為二次組合結構，初始原始高應力軟巖巷道支護結構加固處是否有效融為一體，關鍵在于結合支護承載力。

在設計預測模型之前，需對支護荷載情況進行分析，在高應力軟巖巷道支護體系中通常存在超高壓力的現象，因此設計的預測模型需重點考慮超高壓的情況，設計的高應力軟巖巷道支護加固模型：

式中：H為超高壓系數；ζ為引入功率譜強子；λ為描述軟巖巷道支護結構屬性譜參數；n為中強度破壞等級；η為高應力軟巖巷道支護結構表層支護頻率。

在高應力軟巖巷道支護加固模型的基礎上，得到的破壞生產加速度α如式（5）：

在高應力軟巖巷道支護結構角位移較大處，獲取最佳支護抗毀能力p預測模型：

式中：kj為中強度破壞影響系數最大值；kv為中強度破壞影響系數最小值；tmax為破壞作用時間間隔最大值；tmin為破壞作用時間間隔最小值；k為破壞因子常數。

采用機器學習法對上述公式進行估算，若不考慮應力軟巖巷道支護結構內部存在的擾亂因子，利用所設計的模型，分析預測高應力軟巖巷道支護抗毀變化情況，最終實現中強度破壞力下高應力軟巖巷道支護抗毀性的精準分析。

4 試驗分析

試驗采用基于機器學習的高應力軟巖巷道支護抗毀能力預測方法對中強度破壞力作用下支護抗毀程度進行預測，為精準分析預測結果，以某高應力軟巖巷道支護為試驗對象，分析該結構分別在不同破壞強度下的抗毀程度，支護結構受損程度低，抗毀能力就越強，由此得出基于機器學習在不同破壞力下的抗毀預測結果。

不同支護方案下深部高應力軟巖巷道支護位移，相關參數設置見表2。

表2 相關參數設置Table 2 Related parameters setting

采用文獻［3］、文獻［4］、文獻［5］方法和本文基于機器學習方法分別在M1、M2、M33種不同破壞強度（M1

4.1 M1破壞強度

在M1破壞強度下，分別將2種方法在不同加載時間下抗毀能力預測精準度進行對比分析的結果如圖4。

圖4 M 1破壞強度下4種方法預測精準度對比分析Fig.4 Comparative analysis of prediction accuracy of four methods under M 1 failure strength

由圖4可知，當加載時間為55ms時，采用本文基于機器學習方法預測精準度為95%；而文獻［3］、文獻［4］、文獻［5］方法預測精準度均在80%以下；隨著加載時間的增加，當加載時間到達58ms時，采用本文基于機器學習方法預測精準度仍然為95%，中間呈現波動狀態，但預測精準度均較高，而文獻［3］、文獻［4］、文獻［5］方法預測精準度均呈現波動下降狀態，最終均在60%以下。在M1破壞強度下，本文基于機器學習方法預測精準度較高。

4.2 M2破壞強度

在M2破壞強度下，分別將4種方法在不同加載時間下抗毀能力預測精準度進行對比分析的結果如圖5。

圖5 M 2破壞強度下4種方法預測精準度對比分析Fig.5 Comparative analysis of prediction accuracy of four methods under M 2 failure strength

由圖5可知，采用本文基于機器學習方法預測，在加載時間為55ms時，預測精準度達到最高為94%；而利用文獻［3］、文獻［4］、文獻［5］方法預測精準度均在65%以下。在加載時間為58ms時，本文基于機器學習方法預測精準度達到93%；而文獻［3］、文獻［4］、文獻［5］方法預測精準度均波動下降。在M2破壞強度下，基于機器學習方法預測精準度同樣較高。

4.3 M3破壞強度

在M3破壞強度下，分別將4種方法在不同加載時間下抗毀能力預測精準度進行對比分析的結果見表3。

表3 M 3破壞強度下4種方法預測精準度對比分析Table 3 Comparative analysis of prediction accuracy of four methods under M 3 failure strength

由表3可知，在不同加載時間下，使用機器學習方法在加載時間為58ms時，預測精準度達到最高為98%。而文獻［3］、文獻［4］、文獻［5］方法在加載時間為58ms時，預測精準度最高分別為41%、59%和57%。在M3破壞強度下，本文基于機器學習方法預測精準度最高。

綜上所述：在M1、M2、M33種破壞強度下，本文基于機器學習方法預測精準度均較高，其原因是本文方法在進行高應力軟巖巷道支護抗毀時，巷道在開挖后采取封閉圍巖的保護措施，尤其是對于后期失穩變形的巷道圍巖，加強了對圍巖的保護，在一定程度上節約了高應力軟巖巷道支護抗毀的時間，有利于準確性的提高。

5 結 語

1）基于圍巖強度特性、圍巖屬性及流變特性結合語義特征、深度學習、特征融合方法的思想提出了基于機器學習的高應力軟巖巷道支護抗毀能力預測方法。

2）通過對比現有方法，抗毀能力預測結果與標準分析結果高度一致，且分析耗時較短，是1種有效的抗毀性分析方法。也證明了基于機器學習抗毀能力預測方法的抗干擾能力，為使用更多源項目進行訓練提供了幫助。

3）高應力軟巖巷道支護抗毀能力預測具有巨大應用價值，已經成為熱門研究方向。由于所研究的預測方法并沒有在實際科研環境中得到驗證，因此，提出的基于機器學習的高應力軟巖巷道支護抗毀能力預測已經很好解決了傳統方法存在的數據分布差異性問題，但仍然存在一些不足需要繼續優化。