數控機床主軸系統可靠性分析*
□ 金 城 □ 高 通 □ 懷天澍 □ 楊勝康
1.上海航天精密機械研究所 上海 2016002.西安電子科技大學 機電工程學院 西安 710071
1 分析背景
可靠性是機械零部件的一個重要質量指標特征,受工況、零部件尺寸、安裝精度、材料參數等不確定因素影響。20世紀70年代初,蘇聯首先開展了機床可靠性研究,形成了機床可靠性基礎理論。20世紀80年代,美國也大力開展機床可靠性分析研究。我國在20世紀80年代末開始數控機床可靠性研究。機床可靠性是國內外學者研究的熱點,主軸系統作為數控機床的核心部件之一,研究從未止步。目前,國內外針對數控機床主軸系統的可靠性做了大量研究。張鵬[1]運用故障樹分析與故障模式、影響及危害性分析方法分析了數控機床主傳動系統的可靠性。張李鐵等[2]采用故障模式、影響及危害性分析方法,確定了數控機床主軸系統的故障模式和原因,為數控機床的維修策略提供了參考。籍永建等[3]對機床主軸常見的故障模式進行了分析,并提出了提高主軸可靠性的措施。秦少軍等[4-5]對主軸可靠性的影響因素進行了分析,建立可靠性數學模型進行主軸系統可靠性預測。李兆軍等[6]基于有限元法建立電機組主軸系統的非線性動力學方程,采用可靠性理論及模糊理論構建振動可靠性模糊模型。劉征[7]針對重型數控機床,基于不精確概率理論的混合不確定性統一量化框架,對機床的零部件進行考慮多失效模式相關性的可靠性建模與分析。王德超等[8]采用模糊綜合評判法進行分析,求得機床主軸系統的危害度,并對主軸系統進行了可靠性評價。胡軍[9]根據可靠性分析理論,運用有限元分析軟件的概率設計功能,對數控導軌磨床的主軸進行可靠性分析。劉智鍵等[10]針對機床主軸的可靠性預測需求,提出一種基于蒙特卡洛模擬法的機床主軸可靠度求解方法,有效進行機床主軸的可靠性預測。以上學者圍繞可靠性分析方法、機床主軸系統可靠性分析、主軸系統失效形式等做了大量研究,并取得了許多重要研究成果,但是針對機床主軸系統的可靠性建模大多是基于數據的,當獲得的數據較少或無法獲得數據時,針對主軸系統可靠性建模的研究則較少。筆者將改進一次二階矩法與克里金重要度抽樣方法相結合,提出基于改進一次二階矩法和克里金重要度抽樣方法的考慮主軸軸承動態磨損過程的數控機床主軸系統可靠性分析方法,提高了數控機床主軸系統可靠度的計算效率。
2 改進一次二階矩法
改進一次二階矩法又稱設計驗算點法,以功能函數的線性化泰勒展開點為設計點,該點位于功能函數的失效面上,從根本上解決了一次二階矩存在的問題。
假設結構的極限狀態方程為:
Z=gx(X)=0
(1)
式中:gx(X)為功能函數;X為基本隨機向量。
Z>0,結構處于可靠狀態。Z<0,結構處于失效狀態。Z=0,結構處于極限狀態。
假設x*為極限狀態面上的一點,在x*點處依據泰勒級數展開并取一次項,有:
Z=gx(x*)=0
(2)
(3)
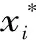
基于符合相互獨立正態分布隨機變量具有線性組合的性質,展開式ZL的均值μZL與標準差σZL分別為:
(4)
(5)
式中:σXi為Xi的標準差。
可靠度指標β為:
(6)
(7)
(8)
式中:Yi為Xi的標準化變量。
基于變量靈敏度因數的方程式為:
(9)
(10)
可靠度指標的幾何意義及設計點如圖1所示。在標準正態空間內,公式(10)為隨機變量的法線式超平面方程,其長度即為可靠度指標β。極限狀態面上的點x*即為設計點[11]。
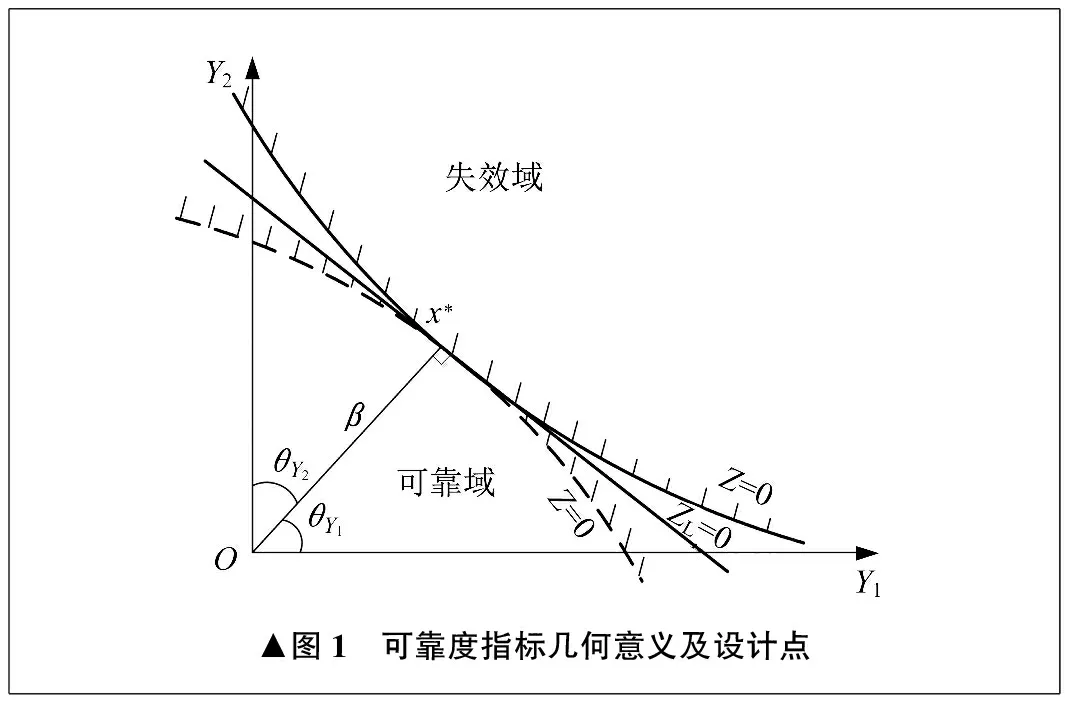
▲圖1 可靠度指標幾何意義及設計點
設計點x*在標準正態空間中可以表示為:
(11)
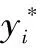
將設計點轉換到原始空間中,有:
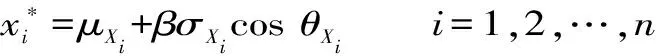
(12)
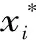
根據上述分析,經反復迭代求解,直至求得滿足迭代要求的可靠度指標。結構的可靠度R為:
R=φ(β)
(13)
式中:φ為標準正態分布函數的累積分布函數。
3 克里金模擬方法
克里金模擬方法是一種改進的線性回歸分析技術,由線性回歸部分和非參數部分兩部分組成,具體模型為:
g(x)=F(β1,x)+z(x)=f(x)Tβ1+z(x)
(14)
式中:g(x)為輸出響應;F(β1,x)為變量β1、x的多項式;f(x)T為變量x的多項式;β1為回歸因數;z(x)提供模擬局部偏差的近似。
z(x)是均值為零的平穩高斯過程,但是該高斯過程的協方差不為零,即z(x)同分布不獨立,空間內任意兩點x、w的協方差為:
(15)
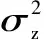
高斯相關函數的計算效率較高,而且其應用范圍是最廣泛的。高斯相關函數為:
(16)
式中:xi和wi為空間內任意兩點x、w的第i個分量;θi為相關性參數;δi為光滑程度參數,一般取2,表示相關方程式無限可微。
給定訓練樣本[x(1),x(2),…,x(p)],x(i)是R域上的第i個樣本點,訓練樣本點的響應為:
Y=[y1,y2,…,yp]
(17)
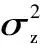
(18)
(19)
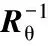
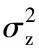
(20)
克里金模型確定之后,可以通過確定的模型預測未知點的響應。假定樣本點為x,基于已經確定的模型,可以估計出新樣本的響應值。克里金預測值的計算公式如下:
(21)
(22)
(23)
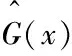
克里金模擬方法是一種精確的插值方法,任意已知訓練點x(i)的預測值G(x(i))是準確的,即:
(24)
4 結構可靠性分析
結構失效屬于小概率事件,對小概率事件進行評估是比較困難的。結構的功能函數越復雜,就越能反映真實結構在隨機變量下的響應,但是復雜的功能函數會導致計算效率下降。針對以上難點,筆者提出克里金重要度抽樣方法,將克里金插值與克里金重要度抽樣方法相結合,基于已知信息及克里金模擬方法建立的插值模型來對結構的響應進行模擬,所需的評估模型通過少量訓練樣本即可確定,對未知樣本點的結構響應預測的準確度比較高。克里金重要度抽樣方法流程圖如圖2所示。
(1) 基于改進的一次二階矩迭代求解狀態方程的設計點。
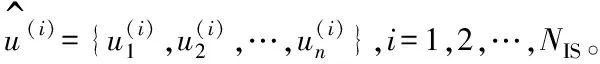
(3) 初始數值試驗設計。這一步驟的主要目的是確定克里金模型的訓練樣本。為了減少模擬過程中的計算量,將步驟(1)計算設計點過程中產生的樣本和對應的功能函數值作為初始訓練樣本及對應的結構響應。
(4) 基于數值試驗設計建立克里金模型。DACE工具箱是應用于軟件的克里金工具箱,被廣泛應用于克里金模型建立及分析中。本方法基于已知的訓練樣本及對應的結構響應,采用DACE工具箱建立克里金模型。
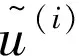
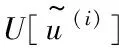
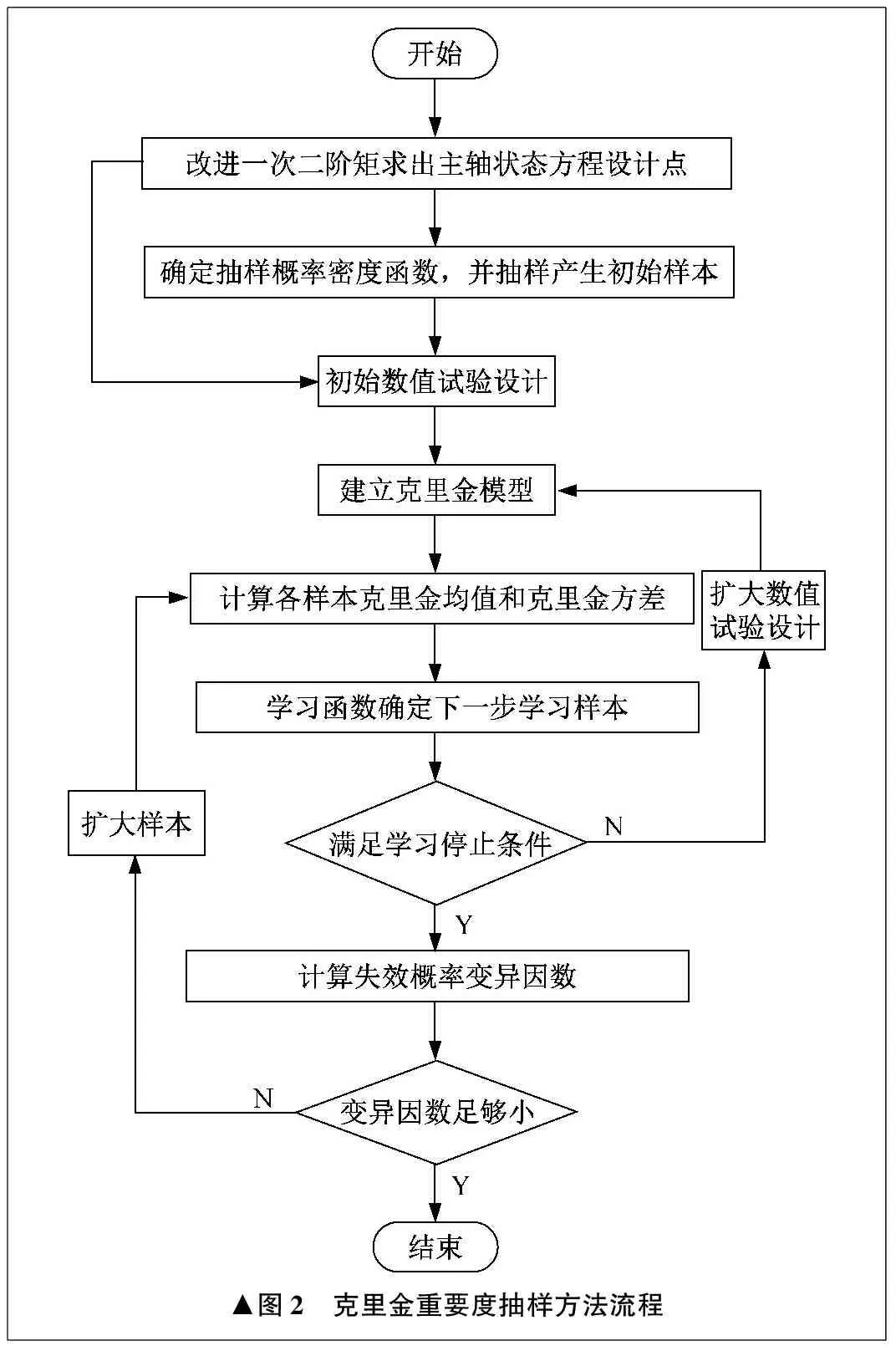
▲圖2 克里金重要度抽樣方法流程
(7) 學習停止條件。通過設置合理的學習停止條件來保證克里金模型的有效性。定義使學習函數最小的那個樣本對應的U值大于等于2時,學習停止,此時表示將所有樣本正確分在安全域和失效域的概率大于97.7%,即結構失效概率可靠度為97.7%。
(8) 擴大數值試驗設計。若步驟(7)中的學習停止條件不滿足,則將學習函數值最小的那個樣本增加到數值試驗設計中,然后基于新生成的訓練樣本點重新訓練克里金模型,直至步驟(7)中的學習停止條件滿足。
(9) 計算失效概率變異因數。若步驟(7)中的學習停止條件滿足,表明在步驟(2)中生成的樣本量下計算出了滿足學習條件的失效概率,但是該樣本量是否已經足夠大,所得到的結構失效概率是否可靠,仍需探討,同時計算預測的失效概率變異因數。
(10) 更新樣本群。為了保證通過克里金預測的結構失效概率是可靠的,若計算的失效概率變異因數過大,則需要增加樣本數量。基于步驟(3)訓練的克里金模型,對更新后的樣本計算克里金均值及克里金方差,直至失效概率變異因數足夠小。此時,通過克里金預測的結構失效概率即為最終的結果。
5 應用實例分析
筆者采用某型號數控機床主軸系統作為應用實例研究對象,其主軸結構如圖3所示。主軸系統采用的角接觸球軸承型號為7210B,具體參數見表1。采用MATLAB軟件進行仿真計算。
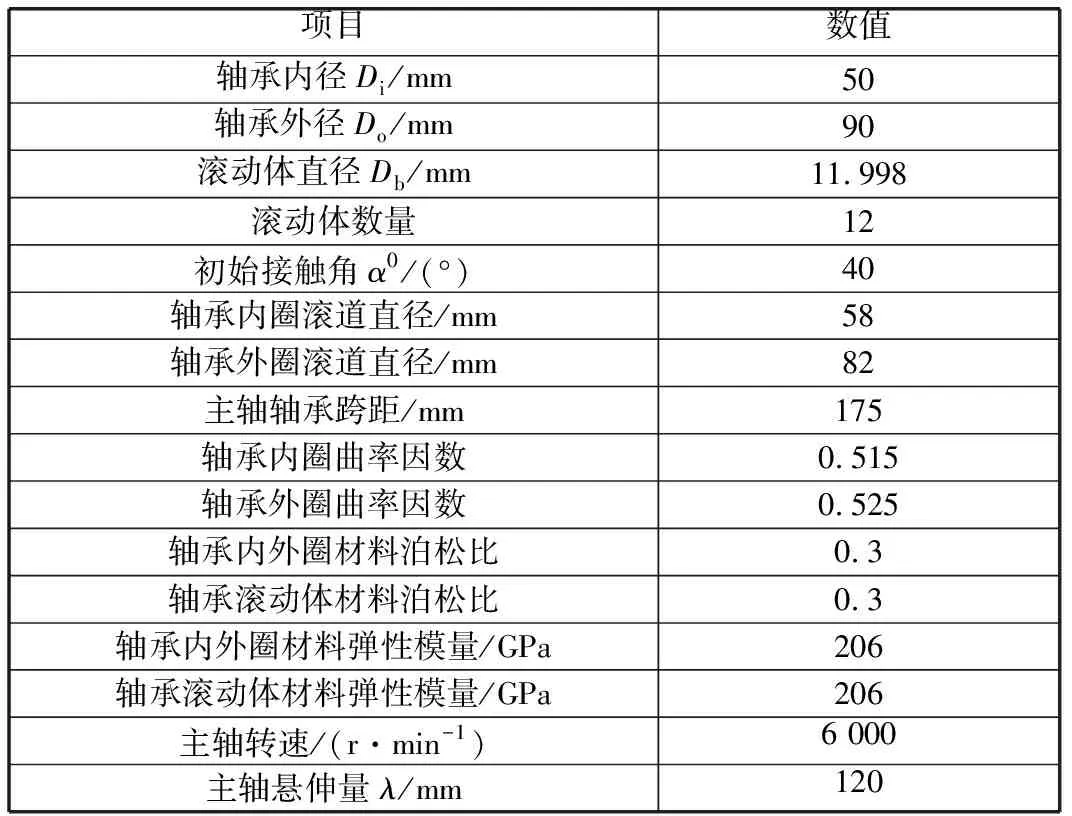
表1 角接觸球軸承參數
建立主軸系統的功能函數為g(u):
g(u)=0.001-Δ′
(25)
式中:Δ′為由磨損引起的主軸軸端徑向跳動。
該精密數控機床主軸系統允許的最大徑向跳動為0.001 mm。
經分析,確定主軸系統可靠性功能函數的隨機變量為:
uT=[Db,Di,Do,α0,λ]
(26)
通過計算及查閱相關資料,獲取各隨機變量的均值,根據公差標準確定各幾何尺寸的標準差。主軸系統各隨機變量均值與標準差見表2。
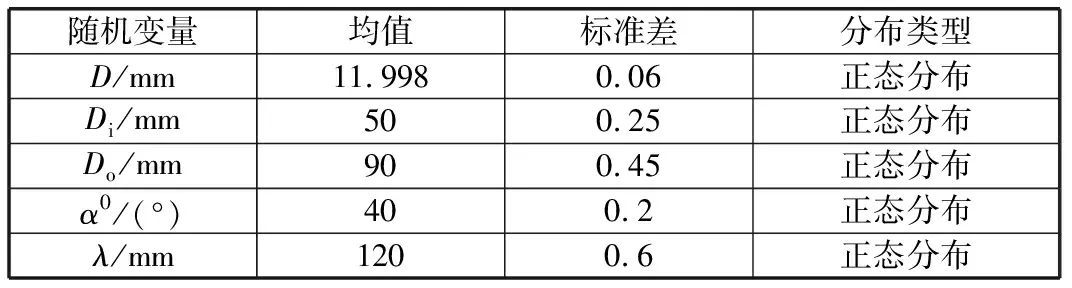
表2 主軸系統各隨機變量均值及標準差
針對可靠性功能函數,基于表2,采用改進一次二階矩法和克里金重要度抽樣方法計算主軸系統可靠度,并與蒙特卡洛模擬法進行對比,可靠度及失效率曲線分別如圖4、圖5所示。蒙特卡洛模擬法與克里金重要度抽樣方法可靠度計算結果對比見表3。
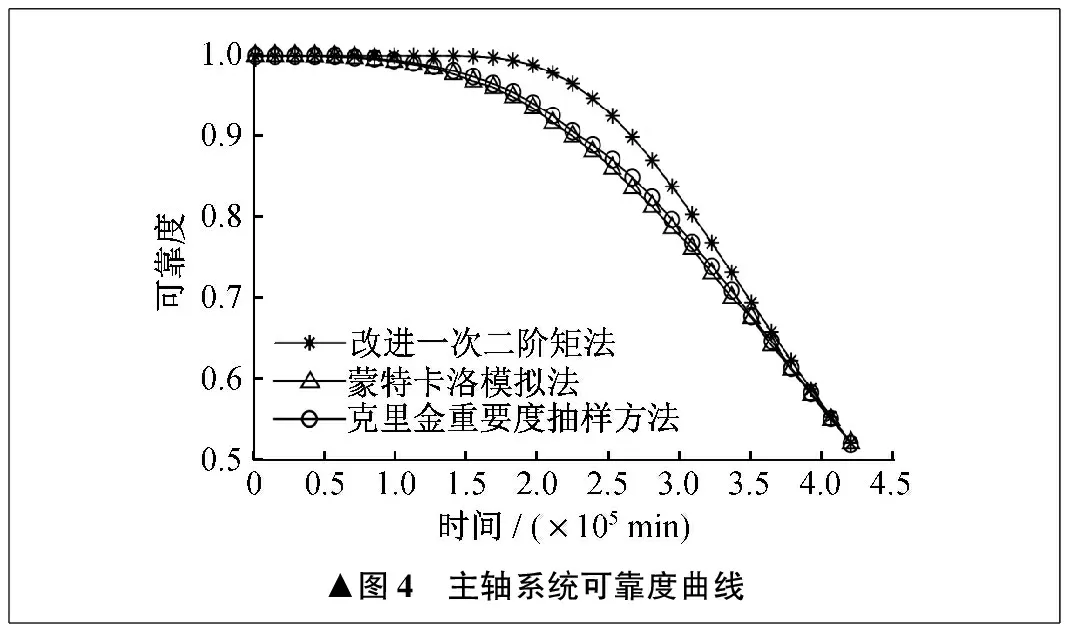
▲圖4 主軸系統可靠度曲線
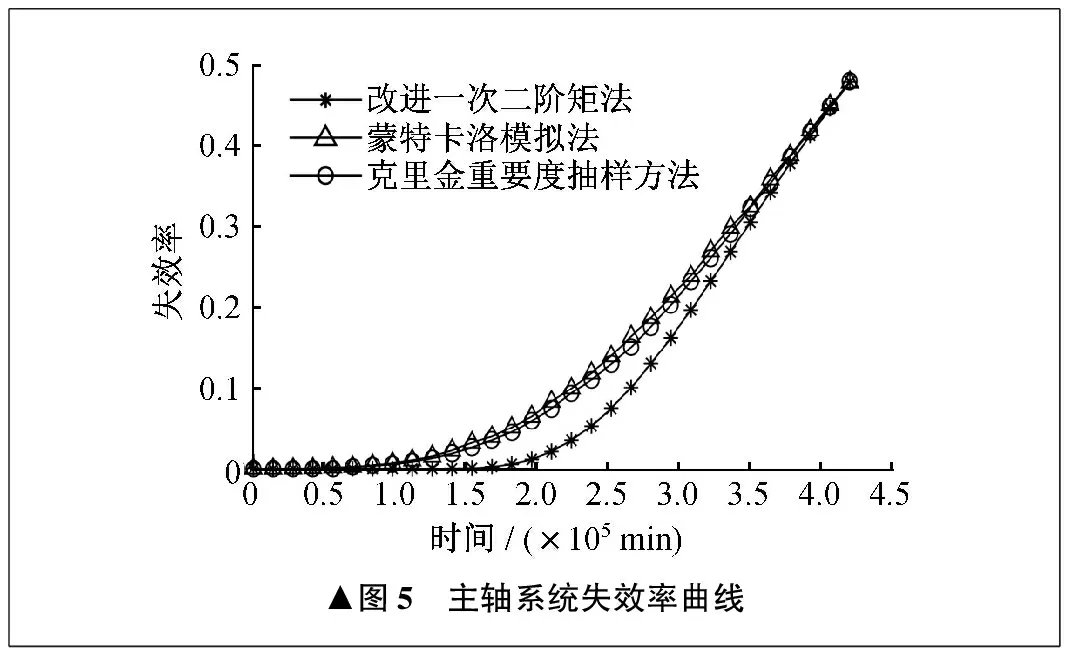
▲圖5 主軸系統失效率曲線
由圖4、圖5、表3可以看出,主軸系統隨著服役時間的推移,可靠度呈現出不同的狀態。0時刻時,主軸系統的可靠度為1。當服役時間小于1×105min時,主軸系統的可靠度曲線較為平穩,主軸系統的可靠度變化不大。當服役時間為4.2×105min時,可靠度降為0.52。
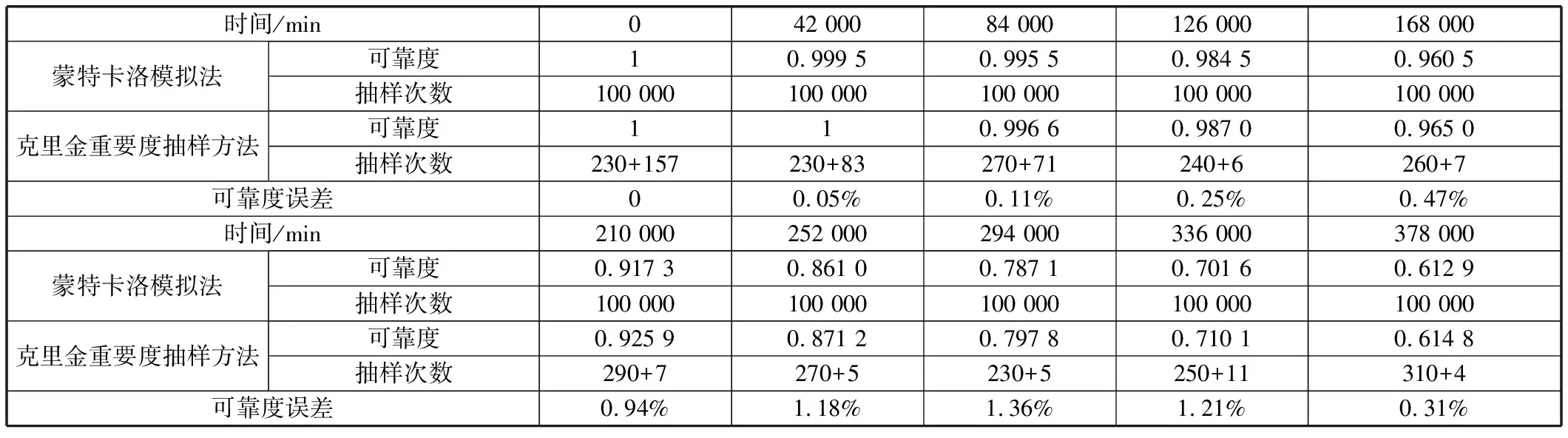
表3 主軸系統可靠度計算結果對比
克里金重要度抽樣方法與直接蒙特卡洛模擬法的計算結果誤差不大,表中給出的結果中最大誤差產生于服役時間為2.94×105min時,計算誤差為1.36%,但是克里金重要度抽樣方法的抽樣次數遠少于蒙特卡洛模擬法,即采用克里金重要抽樣度方法計算主軸系統可靠度時,具有較高的計算效率。
根據圖4及圖5可得,主軸系統的可靠度隨著服役時間的推移不斷降低。隨著軸承磨損量的增大,引起主軸系統軸端徑向跳動量呈增大趨勢,導致主軸系統向性能退化方向發展,從而表現出主軸的可靠度呈不斷下降趨勢。在分析過程中,沒有考慮主軸零件的缺陷、工藝及質量控制等其它失效形式,僅對軸承疲勞磨損引起的主軸軸端徑向跳動進行分析,因此主軸系統的失效率曲線具有浴盆曲線中后半段的特性。
6 結束語
筆者為提高計算效率,將克里金重要度抽樣方法與克里金模擬方法相結合,提出了基于克里金重要度抽樣方法的數控機床主軸系統可靠性分析方法。將計算結果與蒙特卡洛模擬法、改進一次二階矩法的計算結果進行比較,結果表明,基于克里金重要度抽樣方法計算主軸系統的可靠度,效率明顯提高,主軸系統的可靠度隨著服役時間的推移而下降。

