基于改進的蜻蜓算法的特征選擇

劉東強， 陳宏偉

(湖北工業大學計算機學院，湖北 武漢 430068)

近些年來，人們根據生物種群的各種行為，相繼提出了各種各樣的群體智能優化算法，并取得了諸多成果。例如遺傳算法[1]，粒子群優化算法[2]，人工蜂群優化算法[3]，螢火蟲算法[4]等。這些算法被研究者們很好的運用到了社會的各個領域。蜻蜓算法也是一種新穎的元啟發式優化算法，它模擬蜻蜓的群體行為，是由Seyedali Mirjalili為解決連續優化問題在2015年提出的。蜻蜓算法被許多學者研究與運用，如崔學婷等人提出了一種混合改進蜻蜓算法并將其應用于特征選擇[5]；文獻[6]利用二進制蜻蜓算法設計了一種特征選擇包裝器，提高了特征選擇分類效果；王萬良等人為合理應用生產制造中產生的數據,分析和挖掘出數據中的關鍵特征和潛在信息,以幫助企業提高效率、降低成本,提出一種改進的蜻蜓算法,并將其用于特征選擇[7]。為了提高蜻蜓算法的效率與精度，本文提出了一種改進的蜻蜓算法并運用于特征選擇。文章在算法的種群初始化過程中引入混沌策略，并將原來的線性權重做了一個非線性調整，最終用具體的實驗數據驗證了改進后的蜻蜓算法的分類精度更好。

1 蜻蜓算法

蜻蜓算法是一種新的智群優化算法，該算法具有很強的分類搜索能力和迭代優化能力，已在各個領域得到了很好的應用。蜻蜓算法的主要靈感源于自然界中蜻蜓的群體行為[8]。蜻蜓有兩個重要的群體行為：狩獵和遷徙。前者稱為靜態群體，后者稱為動態群體。在靜態群中，蜻蜓會成群結隊，在一個小區域內來回飛行，以捕獵其他飛行的獵物，例如蝴蝶和蚊子[9]。在動態群中，大量的蜻蜓使群在一個方向上長距離遷移[10]。

基于蜻蜓的群體行為，建立了5個數學模型：

1)分離行為(Si)計算如下：

其中X是當前個體的位置，Xj表示第j個相鄰個體的位置，n是相鄰個體的數量。

2)對齊行為(Ai)計算如下：

其中Vj表示第j個相鄰個體的速度，n是相鄰個體的數量。

3)聚集行為(Ci)計算如下：

其中X是當前個體的位置，N是鄰域的數目，Xj表示第j個鄰域個體的位置。

4)覓食行為(Fi)計算如下：

Fi=X+-X

其中X是當前個體的位置，X+顯示食物來源的位置。

5)避敵行為(Ei)計算如下：

Ei=X-+X

其中X是當前個人的位置，X-表示敵人的位置。

在進行蜻蜓個體位置更新時，首先計算步進矢量(ΔX)，步進矢量顯示了蜻蜓的運動方向，并定義如下：

ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+wΔXt

(1)

其中s、a、c、f和e為各自所對應的權重，Si、Ai和Ci分別表示個體的分離、對齊和凝聚力，Fi表示食物的吸引力，Ei表示敵人的影響力，w為慣性權重，t為迭代計數器。

計算步進矢量后，位置矢量的計算如下：

Xt+1=Xt+ΔXt+1

2 改進的蜻蜓算法

在本文中，提出了一種基于混沌理論的新的蜻蜓優化算法。普通的蜻蜓算法和其他許多智能優化算法一樣，在迭代的過程中，很容易陷入局部最優的陷阱，而真正需要的是全局最優值。針對這一缺陷，本文在種群初始化的過程中加入混沌理論，得到覆蓋面更廣的初始種群。為了提高算法的收斂速度，對原蜻蜓算法中的慣性權重w做了一個非線性的調整，大大提高了算法效率與精度。算法的流程圖見圖1。

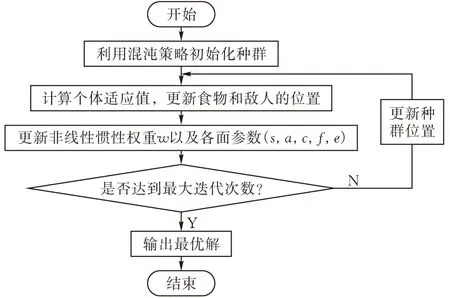
圖 1 算法流程圖

2.1 基于混沌策略初始化種群

本文中，為了提高初代蜻蜓種群的多樣性，而不影響得到的結果，并為算法后期的全局搜索與迭代奠定良好的初始種群基礎。本文在種群初始化的過程中，引用Tent混沌序列的逆混沌映射策略，得到一個品質更優的初代蜻蜓種群。

在本算法中，每個蜻蜓個體的維度為d，在初始化種群的時候，本文首先生成一個d維的蜻蜓個體 (i=1，2,…,n)，然后把生成的個體通過混沌映射，轉化到另外一個解集中去，進而生成一個新的個體CXid(i=1，2,…,n)，計算方法如下：

式中Xid是第i個蜻蜓個體的第d維上的值，Xmind和Xmaxd分別是取值的下界和上界，種群CX={CXi,i=1,2,…,n}是通過混沌映射由種群X={Xi,i=1,2,…,n}變化得到。首先把X和CX兩個種群合并成一個新的蜻蜓種群，其個體數為2n，然后再計算每個蜻蜓個體的適應值，并對得到的所有適應值進行排序，最后取前n個適應值所對應的蜻蜓個體來組成蜻蜓算法的初代種群。

2.2 慣性權重w的非線性改變

在原蜻蜓算法中，式(1)中的慣性權重w是一個線性變化的值，其計算方法見式(2)。在實際情況中，隨著算法迭代次數的增加，算法收斂的速度會慢慢降低，是呈曲線下降的。算法中慣性權重w收斂的速度和算法整體的收斂速度不一致，這就會降低算法的收斂速度，從而影響算法的整體效率。

w=0.9-t(0.5/tmax)

(2)

式(2)中t為當前的迭代次數，tmax為開始設置的總迭代次數。從公式(2)中可以看出，隨著迭代次數的增加，慣性權重w會呈直線趨勢變小。在本文中，引用了指數遞減策略，通過下面公式對慣性權重進行一個非線性的調整改變：

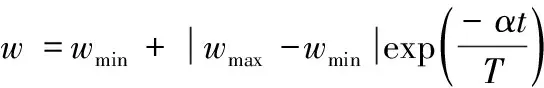
式中wmax和wmin分別為公式(2)中慣性權重w的最大值和最小值：wmax=0.9，wmin=0.4。其中α為調節系數，本文中取α=4，t和T分別為當前迭代次數和最大迭代次數。改進后的慣性權重w和原慣性權重w的對比圖如圖2所示，從圖中可以看出改進后的w是呈曲線下降的，相對于原慣性權重w，其開始的變化速度很快，隨著迭代次數的增加，變化的速度逐漸變慢，這能更好地適應算法的整體收斂速度。

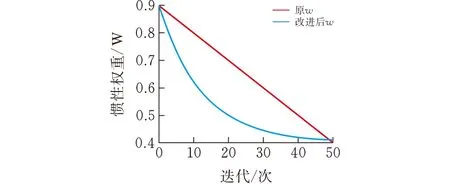
圖 2 權重對比圖

2.3 特征選擇

特征選擇是一種二進制優化問題，個體的位置都是由0或者1來表示。蜻蜓算法能夠很好的解決連續優化問題，它通過將步長向量增加到位置向量的方法來改變個體的位置，但在二進制搜索空間中，種群個體的位置由0和1表示，此方法就不適用了。根據先前Mirjalili和Lewis的研究[11]。可以通過傳遞函數將連續優化算法轉換成二進制算法，傳遞函數一般分為兩種：S型和V型。本文采用V型傳遞函數，將原連續優化算法轉換成了用于特征選擇的二進制優化算法。

3 實驗結果與分析

在實驗中，本文先將改進后的二進制蜻蜓算法(CBDA)與原始的二進制蜻蜓算法(BDA)進行了比較，使用的數據集是兩個UCI數據集：Wine和Sonar。本實驗在Windows10操作系統下進行，電腦的相關配置：操作系統Windows 10, 64 bit，處理器Intel(R) Core(TM) i5-7200U，內存16 G，編程語言Python3.5.2。種群的規模都設置為30，迭代次數都設置為50。通過比較四種算法得到的最優個體的適應值來判斷算法對于文本分類中特征選擇的效果。

實驗結果見圖3、圖4，從圖中可以看出：改進后的二進制蜻蜓算法的收斂速度明顯要好于原算法。

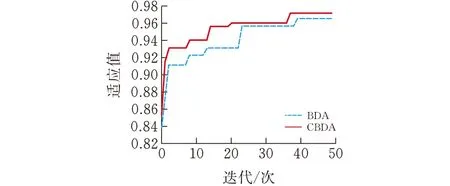
圖 3 在Wine中函數適應度值

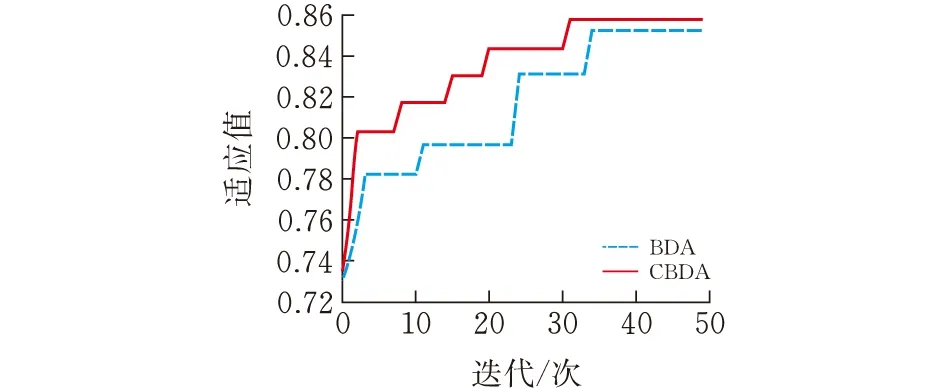
圖 4 在Sonar中函數適應度值

為驗證改進的蜻蜓算法性能，本文還將改進的二進制蜻蜓算法(CBDA)和傳統的二進制遺傳算法(BGA)、二進制粒子群算法(BPSO)進行比較。從30次運行結果中獲取每種算法的平均分類精度，然后相互之間進行比較，得到表1的結果，從中可知改進后的蜻蜓算法的分類精度要好于其他算法。

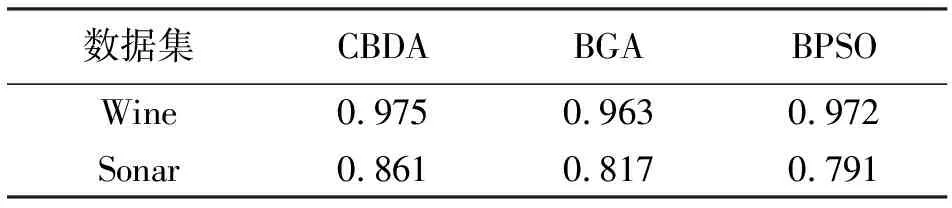
表1 平均分類精度

4 結論

在本文中，將混沌映射和慣性權重的非線性改變運用到蜻蜓算法中，并將改進后的蜻蜓算法運用于特征選擇來檢驗其效果。通過實驗結果可以看出，改進后的蜻蜓算法的收斂速度相對于原算法得到了提高，而且相對于傳統的優化算法，其分類精度也更高。