基于高程異常補償的飛機終端區組合導航高度優化算法

孫淑光,溫啟新

(中國民航大學電子信息與自動化學院,天津 300300)

0 引 言

近年來,我國不管是在軍用航空領域還是民用航空領域,都取得了長足的發展與突破,各地中小型機場不斷涌現,在這些機場起降飛機的數量也在迅速增長。但由于儀表著陸系統(instrument landing system,ILS)地面設施價格昂貴,其制導功能取決于地面設備輻射的空間信號,對安裝場地的要求高[1],很多中小機場沒有配備ILS,這不僅對飛行安全提出了挑戰,還對空管安全保障和服務提出更高的要求[2]。全球導航衛星系統(global navigation satellite system,GNSS)具有定位精度高、服務范圍廣、受天氣影響小等優點,不僅在航空領域發揮重要作用,還與無人化系統、現代通信技術等相互融合,不斷向綜合化、智能化發展,已成為國家基礎設施建設與發展的核心部分[3-5]。ILS作為國際標準的飛機著陸引導系統在二戰末期就已投入使用[6],隨著導航技術的發展,為了增加航空器航路設計的多樣性,提高其在機場終端區域進近路線的靈活性,降低機場著陸引導系統建設成本,國際民航組織(international civil aviation organization,ICAO)已計劃用GNSS來代替ILS完成對航空器的著陸引導[7]。如今北斗導航系統(beidou navigation system,BDS)建設完成并正式開通,這不僅具有極其重要的軍事戰略意義,也為建立新的機場著陸引導系統、研究與發展自主導航性能增強系統等方面提供良好條件[8]。

目前,飛機高度測量主要利用機載大氣數據系統設備,大氣數據系統容易受靜壓誤差影響而導致高度測量精度降低。當飛機所處飛行階段變化時,其飛行氣壓高度參考基準面也會發生變化。當飛機處于巡航階段時,飛行高度的參考基準面為國際標準氣壓海平面(101.325 kPa),而當飛機進入機場管制區域時,飛行高度的參考基準面為修正海平面,不同時間、不同機場區域的修正海平面大氣壓不同。

BDS定位所選取的參考體為CGCS2000參考橢球體[9],其高度基準面與似大地水準面存在差異,該差異被稱為高程異常,ADS測量高度基準面與似大地水準面重合,不同終端區的高程異常不同。由于目前空管運行主要以氣壓基準為依據[10],因此使用BDS接收機測量的高度進行著陸引導時,需要與ADS測量的高度進行組合,消除高程異常的影響。另外,BDS信號在傳播過程中,對流層誤差、電離層誤差[11-12]以及多徑誤差[13]都會影響北斗接收機的定位精度,單獨的BDS接收機高度信息無法滿足民用飛機進近所需導航性能的要求[14]。

捷聯式慣性導航系統(strapdown inertial navigation system,SINS)是一種以牛頓力學為基礎,不依賴于外部信號,根據慣性元件進行全自主式導航的系統,可用于航空器、導彈、車輛以及船艦等多種載體[15]。但其定位誤差隨著時間的積累會逐步增加,高度測量誤差隨時間呈發散狀態[16],在無其他高度測量手段輔助情況下,高度輸出無法滿足飛機高度定位的精度要求。

GNSS與SINS組合導航技術的研究開始于20世紀60年代,根據選取組合系統狀態量的不同,系統組合類型可劃分為:松組合、緊組合和超緊組合[17-18]。針對以上組合方式及特點的不同,國外學者從上世紀開始就進行了研究并應用于制導武器中。在組合過程中,通過Kalman濾波算法,將GNSS的導航信息與SINS的導航信息進行數據融合,利用組合導航系統輸出信息對SINS進行誤差補償,從而使系統保持良好的定位精度,確保載體安全運行。其衍生出來的方法還有擴展Kalman濾波、無跡Kalman濾波、粒子濾波等[19-20],目前已在系統狀態預測、目標跟蹤、故障診斷、衛星導航等多個領域進行應用[21-22]。在高度定位方面,現有的GNSS/SINS組合導航算法未考慮飛機的特定飛行環境與飛行階段,并未將GNSS定位高度與特定地區的高程異常相結合,使其在實際應用中存在一定誤差。國內外針對不同區域,一般采用GNSS與地形輔助導航系統相結合來提高定位精度[23]。但在某些特定地區(如山地、丘陵等),對起伏的地表、復雜的地形進行建模時,其擬合復雜程度要遠大于對其高程異常分布的擬合建模,故本文提出一種基于機場終端區高程異常補償的組合導航算法來提高高度定位精度。

針對3種導航方式的特點及其高度基準的差異問題,本文在對單一導航方式高度測量誤差模型建模及誤差特點分析的基礎上,結合機場所在區域的高程異常模型,通過Kalman濾波方式將3種不同導航方式進行組合,建立組合導航模型并進行仿真,驗證本算法高度優化效果。相比于傳統組合導航算法,本文的主要創新點在于通過對沒有配備ILS的機場終端區高程異常建模,對BDS測量高度進行高程異常補償,并將補償后的BDS與ADS、SINS通過Kalman濾波算法進行組合導航,提高飛機在終端區起降以及進近時的垂直導航精度。通過計算機仿真結果可以看出,該方法在提高飛機垂直導航精度的同時,也解決了在ADS受到靜壓源誤差干擾時,導致系統高度定位精度降低的問題。

1 ADS高度測量及高程異常擬合

1.1 ADS氣壓高度測量誤差模型

ADS以大氣數據計算機為核心,利用安裝在航空器表面的傳感器,探測航空器周圍大氣的靜壓參數,通過氣壓高度方程解算出航空器所在位置的氣壓高度[24-25]。ADS計算標準氣壓高度方程如下:

(1)

式中:Ph為航空器所在氣壓高度的大氣靜壓值；Pb為國際標準大氣條件下,所選氣壓高度基準面的大氣靜壓值；Hb為氣壓高度基準面處的重力勢高度值；g為標準重力加速度值；Tb氣壓高度基準面處的大氣溫度值；L為航空器所在氣壓高度層的氣體溫度垂直變化梯度值;R為理想狀態下航空器周圍大氣氣體常數。

由式(1)可知,氣壓基準面選定后,氣壓高度HP是飛機所在處大氣靜壓Ph的單值函數,大氣靜壓誤差是氣壓高度誤差的主要來源。大氣靜壓誤差一般分為儀表誤差和靜壓源誤差。針對不同飛機機型的儀表誤差,ADS有不同的誤差補償辦法來降低該部分誤差。靜壓源誤差與靜壓孔位置、突風、飛行馬赫數、飛行迎角等有關,飛機在大氣層內做機動飛行或者迎角發生變化時,靜壓傳感器探測到的大氣靜壓Ps就會出現一定的偏差ΔPs。ADS靜壓測量誤差Wp包括靜壓偏差ΔPs和傳感器測量噪聲wp兩部分,表示為

Wp=ΔPs+wp

(2)

1.2 機場終端區高程異常模型及擬合算法

針對機場終端區所在的不同地域,高程異常擬合模型可分為:多項式曲線擬合模型[26]、多項式曲面擬合模型、多面函數擬合模型、BP神經網絡擬合模型等。為確保擬合精度,本文采用多面函數擬合法進行機場區域高程異常補償。多面函數擬合法由美國Hardy教授提出,利用多個簡單的曲面經過疊加后形成一個連續且光滑的曲面,利用該曲面上的點所對應的高程異常來模擬機場區域的高程異常分布,最終達到逼近實際曲面的擬合效果[27]。

假設機場區域實際高程異常分布為曲面函數f(x,y),其逼近函數為φ(x,y),則根據擬合要求:

(3)

φ(x,y)可以描述為

(4)

式中:Qj(·)為基礎疊加曲面的數學表達式(核函數);a為待求核函數權重系數;j為所選核函數個數,取值范圍為1到m;(xi,yi)為高程異常實際測量點的坐標,i表示實際測量點的個數;(xj,yj)為核函數中心的經緯度坐標。

本文選取正雙曲函數作為核函數:

(5)

式中:δ為用來調節核函數形狀的核函數光滑因子。設有n組高程異常實測值(xi,yi),i=1,2,…,n,對應的高程異常值為ξi,i=1,2,…,n。則每一個實測點的誤差方程為

(6)

用矩陣形式表示為

(7)

根據最小二乘法計算求得核函數權重系數矩陣A=(QTQ)-1QTξ,將所求得的核函數權重系數帶入到表達式φ(x,y)中,就可得到機場區域實際高程異常分布的逼近擬合函數。最后利用飛機接收的GNSS導航信息,解算出飛機所在機場終端區域的經緯度,將此位置信息帶入到機場終端區高程異常擬合函數中,即可得到飛機具體飛行位置對應的高程異常值。

2 ADS/SINS/BDS組合導航模型

2.1 組合導航整體架構

ADS/SINS/BDS組合導航系統整體架構如圖1所示,包括ADS模塊、SINS模塊、BDS模塊、高程系統模塊和卡爾曼濾波模塊。其中BDS解算出的高度信息與高程異常模塊提供的機場區域高程異常信息相結合,構成新的高度信息,也即相對于機場場面的高度信息。卡爾曼濾波模塊將BDS輸出的位置信息,ADS模塊輸出的氣壓高度信息,SINS模塊解算出的位置、速度信息進行數據融合,即可輸出高度的最優濾波估計值。通過圖1可以看出,本文所提出的高程異常補償算法主要是對BDS測量高度進行補償。當飛機進入機場終端區時,其飛行高度參考基準面為當地的修正海平面,該基準面為ADS測量氣壓高度的參考基準面。而BDS測量高度的參考基準面為CGCS2000國家大地坐標系參考橢球面。兩個系統測量高度的參考基準面在不同位置具有一定的數值差異。為統一不同導航系統的測高參考基準面,提高定位精度,需對這部分差異進行補償。其具體步驟為:① 當飛機進入機場終端區時,通過輸入接收BDS定位的經緯度信息,根據所建立的機場終端區高程異常分布模型,可計算出飛機所在位置的高程異常值。② 將飛機所在位置的高程異常值對BDS測量的對應位置高度信息進行補償計算,從而使BDS測高參考基準面與ADS測高參考基準面統一。③ 將不同導航系統通過卡爾曼濾波進行組合導航,提高系統定位精度。

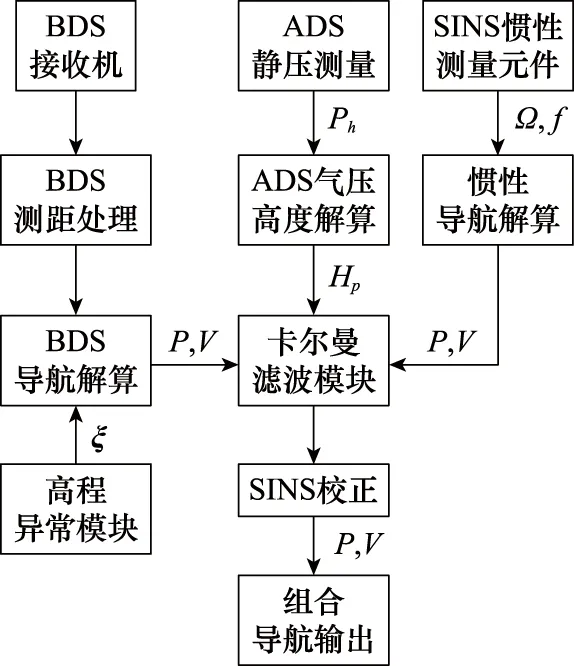
圖1 組合導航系統架構圖Fig.1 Architecture diagram of integrated navigation system

2.2 狀態方程的建立

在ADS/SINS/BDS松組合濾波模型中,采用位置、速度組合方式,選取SINS的誤差參數作為濾波的狀態變量。SINS誤差包括:大地坐標系下的經度誤差,緯度誤差與高度誤差,站心坐標系坐標系下的速度誤差、載體坐標系下的姿態角誤差、慣性元件誤差。組合導航系統狀態方程為

(8)

式中:X為系統狀態矢量矩陣,具體表示為

X=[X1,X2,X3,X4]T

(9)

(10)

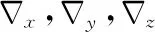
(11)

W為系統過程噪聲矩陣,表達式為

W=[wbx,wby,wbz,wax,way,waz]T

(12)

式中:wbx,wby,wbz為機體坐標系下的陀螺儀隨機噪聲;wax,way,waz為機體坐標系下的加速度計隨機噪聲。系統狀態轉移矩陣F可由SINS誤差微分方程推導得出[28]。

2.3 基于影響因子β的量測方程的建立

文章假設飛機的真實位置為L、λ、h,真實速度為ve、vn、vu,則SINS解算的位置信息和速度信息可分別表示為

(13)

(14)

式中:δLI,δλΙ,δhI為SINS位置測量誤差；δvIe,δvIn,δvIu為SINS東北天坐標系下速度測量誤差。BDS解算的位置信息和速度信息分別表示為

(15)

(16)

式中:δLB,δλB,δhB為BDS位置測量誤差;δvBe,δvBn,δvBu為BDS速度測量誤差。

ADS解算的高度信息可表示為

hA=h+δhA

(17)

式中:δhA為ADS氣壓高度測量誤差。

當飛機進入機場管制區域時,飛行員會根據地面播報的當地修正海壓,對ADS的氣壓基準進行修正。此時,如果ADS高度測量準確(靜壓源誤差較小),可利用ADS和SINS的高程差進行高度的濾波修正。但如果ADS氣壓高度受靜壓源誤差影響較大,則會對高度導航精度產生影響。而BDS不受天氣因素影響,故在飛機靜壓源誤差增大時,將Kalman濾波的高度量測方程轉換為BDS測量高度hB與SINS測量高度hI之差。因此,量測方程中高度誤差方程表示為

Δh=β(hI-hB)+(1-β)(hI-hA)

(18)

式中:β為ADS誤差判斷因子。

根據文獻[29]仿真結果,當飛行迎角在-5°～0°范圍內時,ADS的靜壓源誤差影響可忽略不計,此時,β值設為0;當迎角不在該范圍內時,ADS高度受靜壓源誤差影響較大,β值由0變為1,ADS模塊輸出的氣壓高度值將不再參與系統量測值計算。Kalman濾波系統量測方程表示為

(19)

量測噪聲轉移矩陣為

(20)

量測噪聲矩陣為

(21)

式中:Rm為地球子午圈半徑;Rn為卯酉圈半徑。

2.4 ADS/SINS/BDS組合導航Kalman濾波實現

組合導航的狀態方程和量測方程經離散化后可寫成如下形式:

(22)

式中:Φk,k-1表示離散化后的系統狀態一步轉移矩陣;Γk-1表示離散系統噪聲分配矩陣;Wk-1表示系統噪聲矩陣;Hk表示離散系統量測轉移矩陣;Vk表示量測噪聲矩陣。

Kalman濾波算法主要包括下5個步驟。

步驟 1系統狀態一步預測方程:

(23)

步驟 2系統狀態估值計算方程:

(24)

步驟 3Kalman濾波增益計算方程:

(25)

步驟 4系統一步預測均方誤差矩陣計算:

(26)

步驟 5系統估計均方誤差矩陣計算:

Pk=(I-KkHk)Pk,k-1

(27)

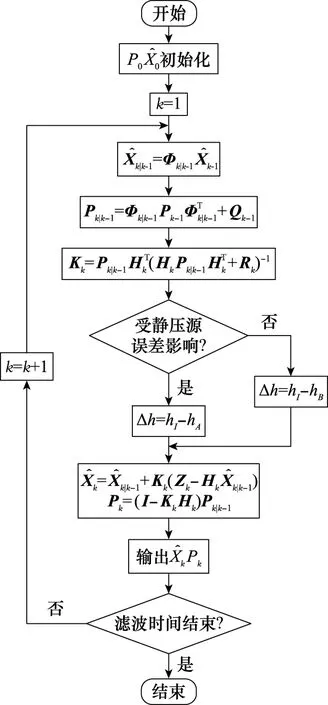
圖2 Kalman濾波流程圖Fig.2 Flow chart of Kalman filtering

ADS測量誤差增大情況下,為有效提高高度導航精度,BDS/SINS高度信息融合前,首先通過高程異常補償對BDS接收機所測得機場附近區域高度進行優化補償,調整高度基準,確保飛機真實離地高度與導航系統提供高度的一致性及準確性。圖2中初始點為0時刻對狀態估計協方差矩陣P0與選取的系統狀態量X0的初始化。整個算法流程中的關鍵拐點為通過判斷系統是否受靜壓源誤差影響后,確定Δh值的具體計算方法。

3 組合高度解算仿真與結果分析

3.1 仿真模塊設置

為驗證高程異常補償下的ADS/SINS/BDS組合導航算法的有效性和可行性,本文利用機場附近區域的數據進行了仿真。仿真模塊包括:航跡生成模塊,ADS仿真模塊,SINS仿真模塊,BDS仿真模塊,Kalman濾波模塊和高程異常模塊。航跡模塊能夠模擬飛機起飛、爬升、平飛、轉彎、俯沖等飛行狀態,并且能夠給出飛機飛行位置、速度、加速度、姿態角等飛行參數,ADS仿真模塊提供相應的氣壓高度信息,SINS模塊提供捷聯式慣性導系統解算的位置,速度信息,BDS模塊提供北斗系統解算的位置信息,高程異常模塊給出飛機所在機場附近的高程異常值,Kalman濾波模塊對導航信息進行數據融合,輸出組合導航信息,仿真流程如圖3所示。

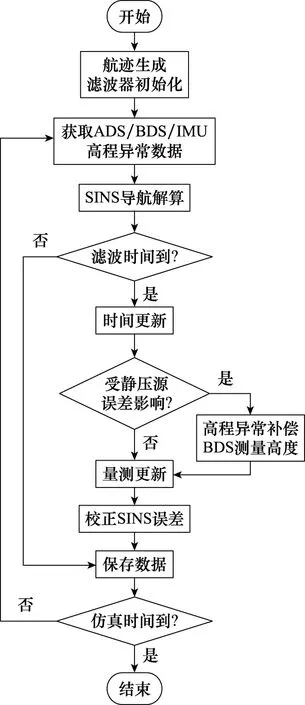
圖3 系統組合導航流程圖Fig.3 Flow chart of system integrated navigation

3.2 仿真結果與分析

進近中的飛機三維航跡如圖4所示,初始經度為東經115°,初始緯度為北緯22°。仿真條件設置如表1所示,N(a,b)表示均值為a,方差為b的高斯白噪聲。

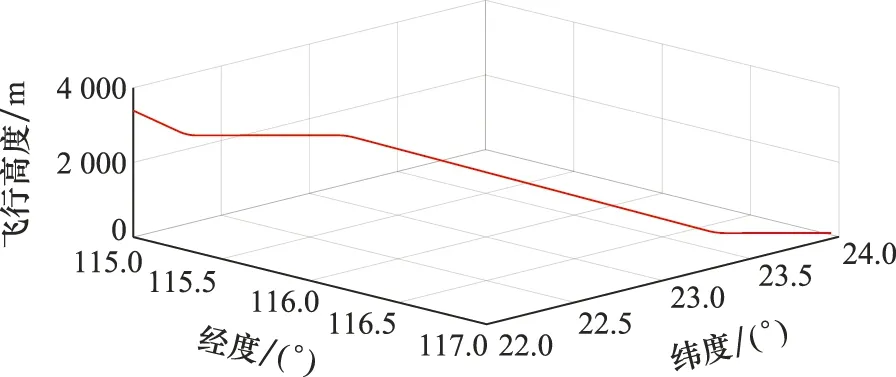
圖4 三維飛行航跡圖Fig.4 Three dimensional flight path diagram

表1 仿真條件及參數設置Table 1 Simulation conditions and parameter settings

高程異常曲面擬合采用多面函數擬合法,核函數平滑因子為0,可表示為

(28)

(29)

(30)

(31)

選取的高程異常實際測量位置為:(21°/E,113°/N),(22°/E,117°/N),(25°/E,116°/N)。考慮測量誤差,高程異常值測量值中加入標準正態分布的高斯白噪聲,其擬合結果如圖5所示。

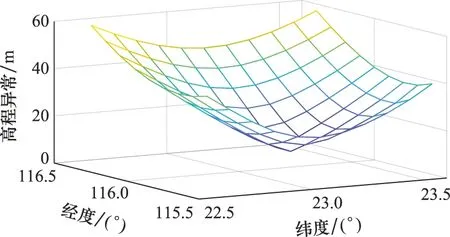
圖5 機場終端區的高程異常曲面擬合Fig.5 Height anomaly fitting map of airport terminal area

在本文仿真條件下,ADS,SINS,BDS高度測量誤差曲線如圖6所示。

圖6 單一導航系統高度測量誤差曲線圖Fig.6 Height measurement error curve of single navigation system

由圖6可以看出,在仿真時間內,SINS高度測量誤差隨時間由0 m增長至70.82 m,誤差隨時間的積累而增加。未受靜壓源誤差影響條件下,ADS高度測量誤差范圍為-12.94～10.55 m,BDS高度定位誤差范圍為11.22～49.05 m。

圖6中的BDS測量高度受終端區高程異常影響。對終端區高程異常補償之后,BDS高度定位誤差曲線圖如圖7所示。

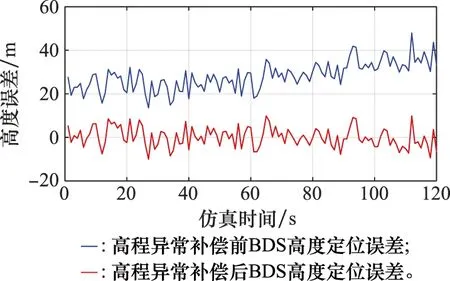
圖7 高程異常補償前后BDS高度定位誤差曲線圖Fig.7 BDS height positioning error curve before and after height anomaly compensation

由圖7可知,補償終端區高程異常前,BDS高度定位誤差范圍為11.22～49.05 m。補償終端區高程異常后BDS高度定位誤差范圍為-17.55～13.93 m。在仿真條件下,通過終端區高程異常補償,BDS接收機測量的對地高度誤差減少33.16%。

在仿真時間80～100 s之間加入靜壓源誤差Wp,其中靜壓源偏差ΔPs為300 Pa,傳感器測量噪聲wp是均值為0,方差為10的高斯白噪聲。此時的Kalman濾波仿真波形如圖8所示。

圖8 靜壓源誤差影響的Kalman濾波高度誤差圖Fig.8 Kalman filter height error diagram affected by static pressure source error

由圖8可知,存在靜壓源誤差時,ADS高度定位誤差范圍為-18.02～39.05 m。根據本文算法,當ADS檢測到有較大的靜壓誤差影響時(攻角不在-5°～0°范圍內),系統量測方程中的高度分量將由SINS測量高度與補償終端區高程異常后的BDS測量高度的差值作為量測值。由圖8中可以看出,改變高度量測的組合信息后,使得系統在靜壓源誤差影響階段的高度定位誤差減少了41.52%,降低了靜壓源誤差所造成的影響。

圖9為組合導航系統在東北天坐標系下的位置誤差。將改進的Kalman濾波、傳統Kalman濾波與SINS東北天方向的定位誤差作對比。

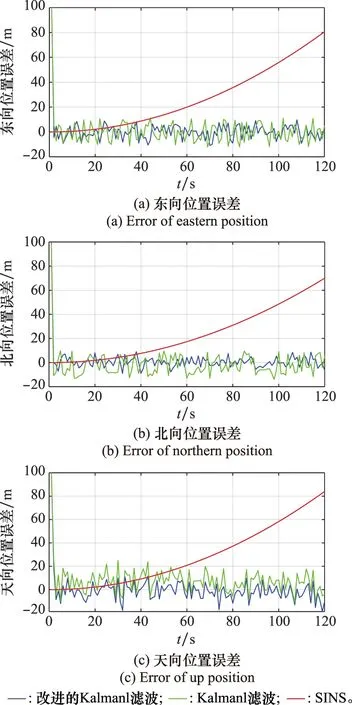
圖9 組合導航位置誤差Fig.9 Position error of integrated navigation

從圖9中可以看出,SINS在東北天方向的定位誤差都存在不同程度的發散。改進的Kalman濾波算法與傳統的Kalman濾波算法相比,其改進之處主要體現在天向定位誤差方面。在天向位置,SINS定位誤差范圍為0～83.25 m,改進的Kalman濾波算法定位誤差范圍為為-19.75～11.37 m,傳統Kalman濾波算法定位誤差范圍為-15.86～24.63 m。通過對機場終端區高程異常的補償,可在原有的Kalman濾波算法的基礎上進一步縮小高度定位誤差波動范圍,提高高度的定位精度。改進后的Kalman濾波算法在提高高度定位精度的同時,仍可起到抑制SINS的定位誤差發散的效果,保證系統有良好的濾波輸出。

4 結 論

本文針對無ILS引導的機場終端區,利用Kalman濾波算法對ADS/SINS/BDS測量數據進行優化融合,提高了飛機高度測量精度。針對飛機進近階段受到靜壓源誤差影響高度測量變差的情況,利用機場終端區高程異常補償算法,將ADS所測高度轉變為不受靜壓源誤差影響的BDS測量高度,確保了飛機離地高度測量的準確度。通過仿真可以看出,本文所改進Kalman濾波算法可以有效抑制SINS測量誤差隨時間增加而發散的情況,且在飛機受到靜壓源誤差干擾時,通過高程異常補償,有效提高了飛機飛行高度的定位精度,增強了飛機進近階段的安全性,為無ILS終端區飛機進近的高度解算優化算法提供了參考。