高壓共軌系統關鍵參數對油壓波動的影響

張熙燁，陳相安，李思哲，仲皓，張學敏

(中國農業大學工學院，北京 100083)

隨著排放法規的日益嚴格，人們對柴油機燃燒性能、噴射噴油規律以及排放水平等方面的要求也越來越高[1]，高壓共軌系統(Common Rail System，CRS)因其具有優化燃燒、可獨立控制噴油壓力、能有效降低排放和油耗的突出優勢，已成為當前柴油機的主要研究方向[2-3]。

CRS主要由電控單元、高壓油泵、共軌管、電控噴油器等部分組成[4-5]，其中高壓油泵僅向共軌管供油維持共軌壓力，采用壓力-時間式燃油計量原理，用高速電磁閥控制噴射過程。但噴油器針閥受外力作用驅動，其開啟回落在蓄壓腔和共軌管內都會產生壓力波，并隨著連接管路傳播擴散，造成噴油壓力波動，影響噴射精確性[6]。而壓力波動會引起噴油量變化，壓力對噴油器內部流動狀況的影響直接影響噴油質量及排放[7]。關于高壓共軌系統中的油壓波動問題，一直以來在世界范圍內都被廣泛研究。N.A.Henein等[8]采用噴油率試驗臺及單缸柴油機研究了柴油機噴油的壓力波動特性，指出隨共軌壓力提高實際噴油時間與信號指令之間的間隔會縮短，增加噴油時間，造成噴油量不準確；G.M.Bianchi等[9]采用一維/三維耦合仿真的方法建立共軌系統噴油器模型，通過改變高壓泵噴油壓力，對不噴射、單次噴射、多次噴射情況下共軌管內的壓力波動進行了研究，發現共軌控制腔內壓力波動的傳播和振蕩對多次噴射的油量有較大的影響，建議通過改變機械結構參數降低波動的影響。馬修真等[10]利用在AMESim仿真平臺建立高壓共軌系統數值仿真模型的方法，發現循環噴油量隨著參數變化而產生波動，并指出在全工況平面內，回油壓力、控制閥桿升程、進油孔直徑、出油孔直徑、針閥升程和噴油器流動系數為影響流量波動的6個關鍵參數，是高壓共軌噴油系統參數優化的主要目標。

為更好地分析高壓共軌系統關鍵參數對油壓波動的影響，為后續柴油機高壓共軌系統的設計開發、模擬計算等提供更加準確的數據支持和邊界條件，本研究應用AMESim仿真平臺對高壓共軌系統進行了建模，并通過試驗對模型的準確性進行驗證，在此基礎之上對CRS各參數對共軌管內壓力波動的影響進行研究，分析影響波動的主要因素。

1 模型建立及試驗驗證

1.1 高壓共軌系統仿真模型的建立

本試驗采用的CRS900高壓共軌試驗臺由高壓共軌噴射系統、380 V三相交流變頻驅動系統、控制系統、傳動系統以及油路系統組成。基于對高壓共軌系統的認識及對CRS900共軌試驗臺的實際測量分析，應用AMESim仿真平臺對試驗臺搭載的高壓共軌系統進行完整的建模[11-13]，仿真模型見圖1。

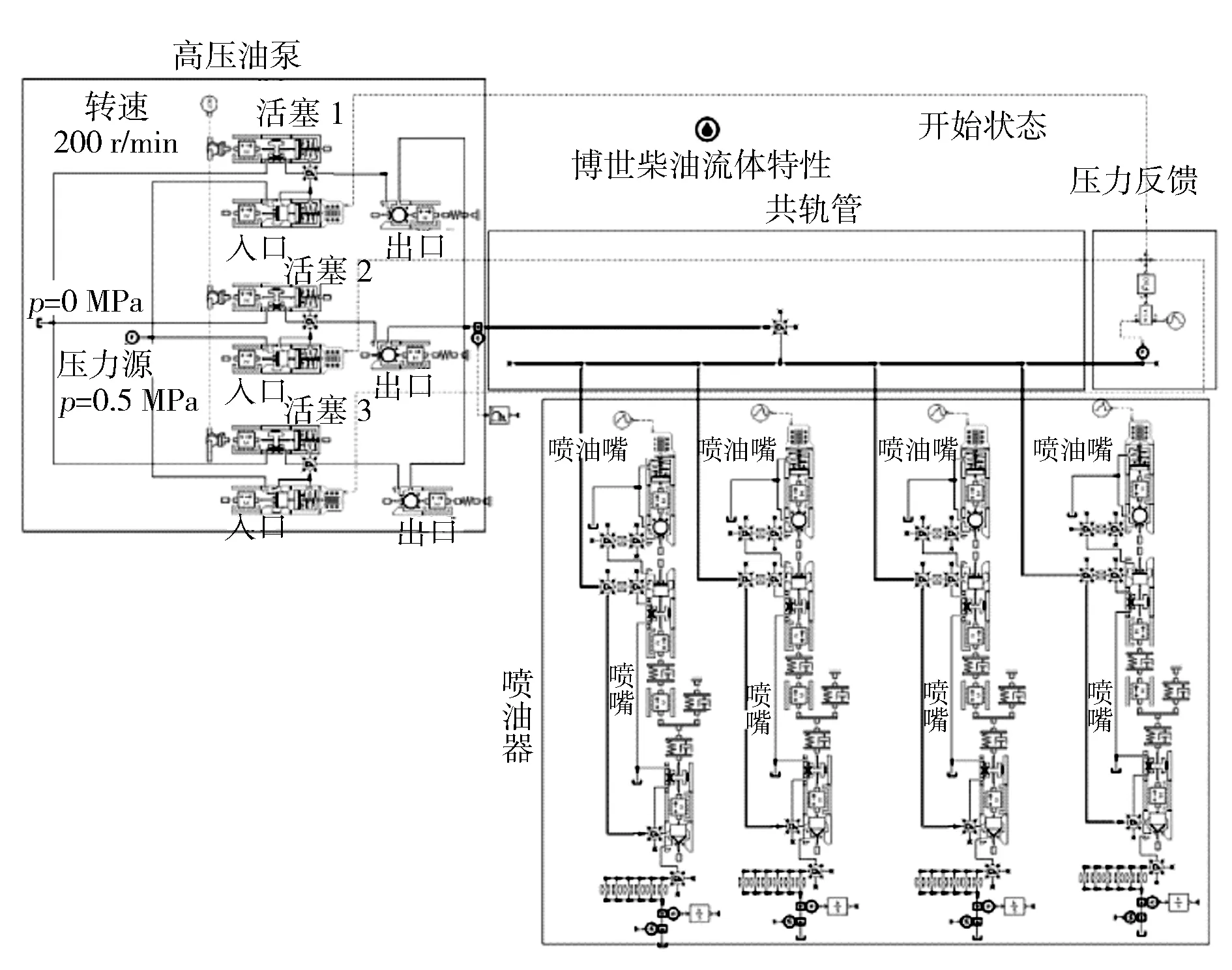
圖1 高壓共軌系統仿真模型

模型定義了系統中油液的特性，包括密度、黏度、氣體溶解量等，此次仿真液體特性選用的是0號柴油，密度為0.84 kg/L，凝點為0 ℃，沸點為180～370 ℃。

1.2 試驗驗證

在CRS系統中，高壓油泵轉速與整機轉速成固定比例關系。本研究中選取轉速比為1∶2，選取柴油機中間轉速1 600 r/min為試驗轉速，此時高壓油泵轉速穩定在800 r/min。試驗中固定轉速在800 r/min，加載油壓，待轉速平穩且油軌油壓基本穩定時開始試驗。

試驗中分別測定了不同條件下的噴油量。首先設定油壓分別為40 MPa，60 MPa，80 MPa，100 MPa，分別記錄在不同噴油脈寬、固定噴油次數條件下的噴油量；然后設定固定噴油脈寬分別為0.6 ms，0.8 ms，1.0 ms，1.2 ms，調整噴油壓力，測量固定噴油次數條件下的噴油量。通過計算得出各工況下的單次循環噴油量，部分試驗與仿真數據對比見表1。

由表1數據可見，各個軌壓下仿真噴油量與試驗值之間的平均誤差小于5%，在允許范圍以內，且可以看出所有工況條件下噴油量仿真值與試驗值變化趨勢一致，該仿真模型與CRS900試驗臺搭載的CRS系統噴油特性相近。由以上分析可得，該仿真模型與實際共軌系統相比具有較高吻合度、較好的準確性和較好代表性，可以利用該仿真模型來進一步模擬研究CRS900試驗臺所搭載的CRS系統的特性。

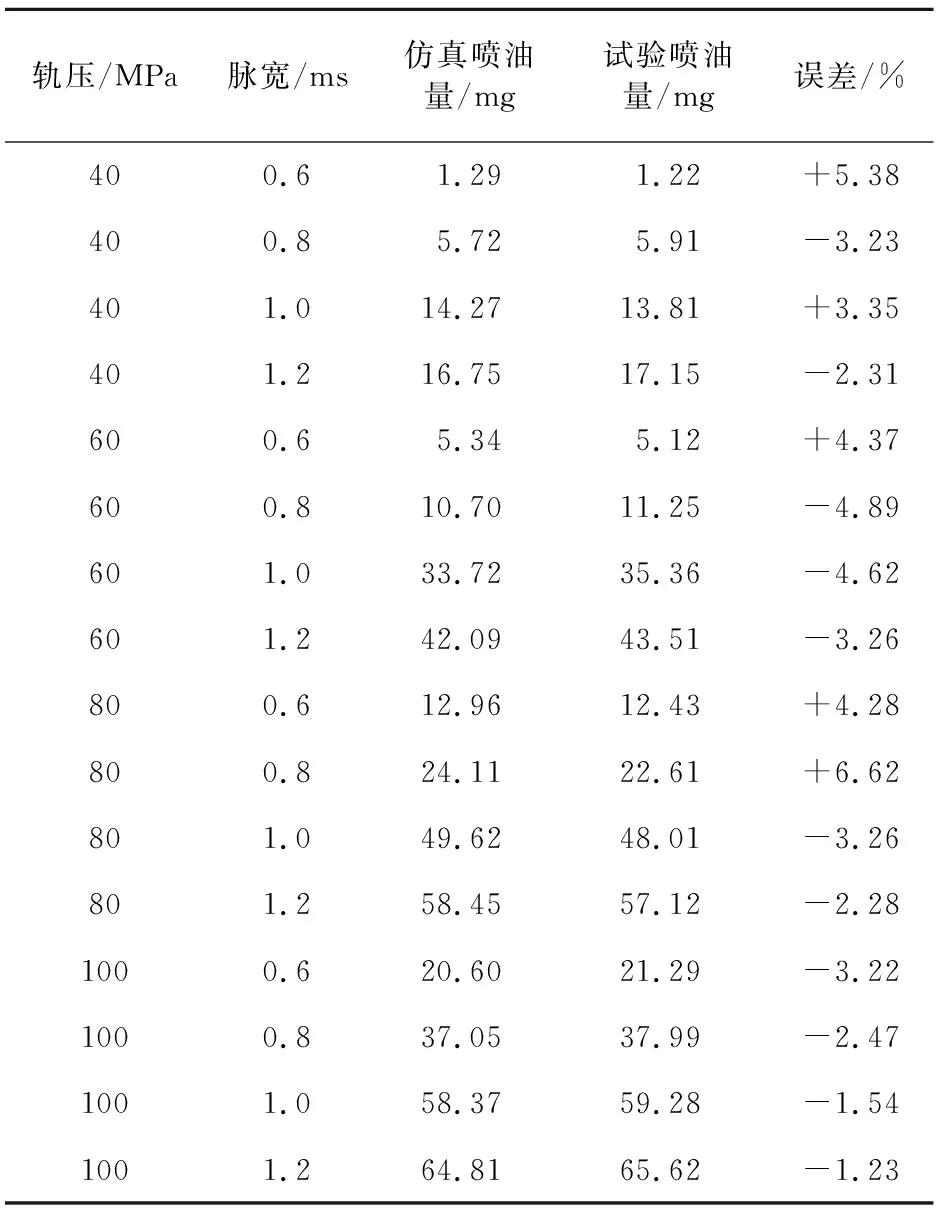
表1 部分試驗與仿真噴油量數據對比

2 仿真試驗與分析

高壓共軌系統參數在生產裝配和使用過程中的變化會引起循環噴油量的波動，從而造成噴油系統工作穩定性的下降。為此分別對噴油壓力、噴油脈寬、共軌管直徑3個主要高壓共軌系統參數值對共軌管內油壓波動的影響進行仿真試驗，分析各參數對油壓波動的影響。

2.1 噴油壓力對油壓波動的影響

圖2示出固定共軌管和高壓油管的長度和直徑，脈寬1 ms，不同軌壓時共軌管內的油壓波動。噴油器從0 ms時刻開啟噴油，持續1.2 ms后落座。由圖2可知，共軌管內的油壓波動幅值隨著噴油壓力的增大呈現增大趨勢。且隨著軌壓逐步增大，噴油器噴油后管內油壓波動頻率升高。

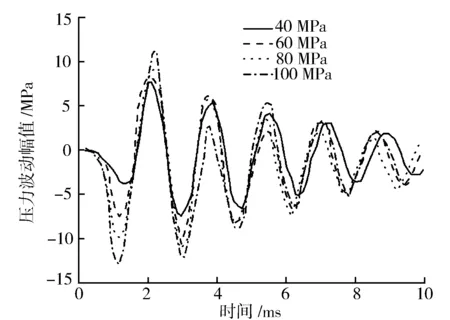
圖2 軌壓對壓力波動的影響

由于在相同軌壓不同噴油脈寬條件下，不同脈寬對應的壓力波動隨時間的變化在針閥開始落座關閉前處于基本吻合的狀態，所以應用此規律確定針閥開始關閉的點。

圖3至圖6示出4種軌壓下1.0 ms以及1.5 ms噴油脈寬所對應的油壓波動規律，且在圖中標識出了兩種脈寬的壓力波動分離點A，即為1.0 ms的脈寬對應的噴油器針閥開始回位關閉的時刻。當噴油器針閥開始落座時，噴油壓力開始回升，軌壓逐步升高，針閥抬起后，管內壓力下降幅度也隨之升高，這是由于軌壓增大導致燃油噴射能力增大，相同噴油脈寬下噴出的燃油量隨軌壓升高而增大，且單位時間內泄壓量較大，進而增大了初次的油壓波動幅度。隨后電磁信號斷開，針閥開始回位，此時共軌管內油壓開始逐步回升。軌壓還影響著壓力波動的頻率，軌壓升高，壓力波動頻率同樣升高。

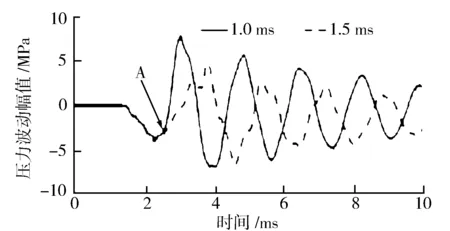
圖3 40 MPa軌壓下的油壓波動

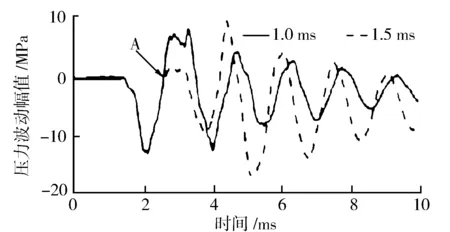
圖4 60 MPa軌壓下的油壓波動

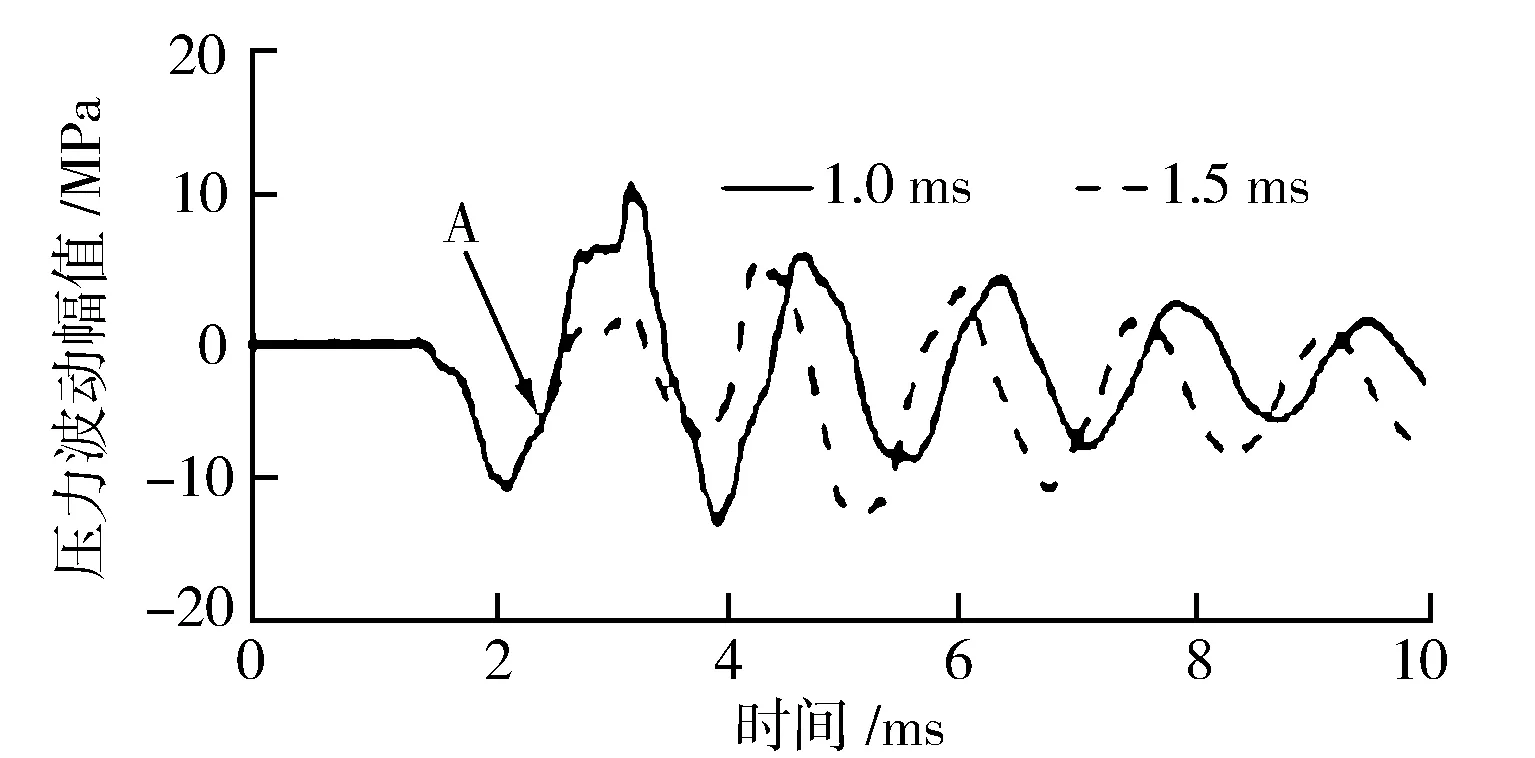
圖5 80 MPa軌壓下的油壓波動

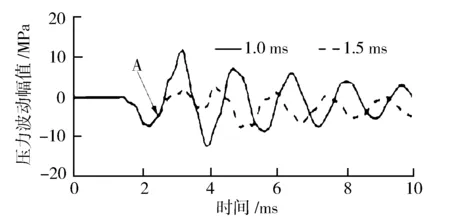
圖6 100 MPa軌壓下的油壓波動

因此，從整體上看，壓力波動幅度隨著軌壓增加而增大。

2.2 噴油脈寬對油壓波動的影響

圖7示出噴油壓力為60 MPa，高壓油管長度和直徑固定，不同噴油脈寬時的共軌管內油壓幅值波動隨時間的變化。在噴油脈寬從0.2 ms遞增至0.8 ms的過程中，壓力波動幅值隨著脈寬的增加而增大。為了在圖中表述清晰，沒有將0.8 ms的波動曲線繪出。在脈寬繼續從0.6 ms增大至1.0 ms的過程中，壓力波動幅度隨噴油脈寬的增大呈現出與之前不同的變化趨勢，此時油壓波動幅值隨脈寬的增大而減小，當繼續增大脈寬，波動幅值轉而增大。

圖7 60 MPa時脈寬對壓力波動的影響

為了更清楚地說明噴油脈寬這一單一變量與油壓波動之間的影響規律，仿真得出20 MPa和100 MPa兩種相差較大的噴油壓力下，噴油脈寬從0.8 ms連續變化至1.4 ms，步長為0.2 ms時，油壓波動隨時間的變化，結果見圖8和圖9。

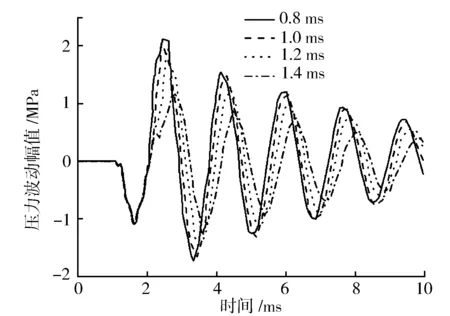
圖8 20 MPa時噴油脈寬對壓力波動的影響

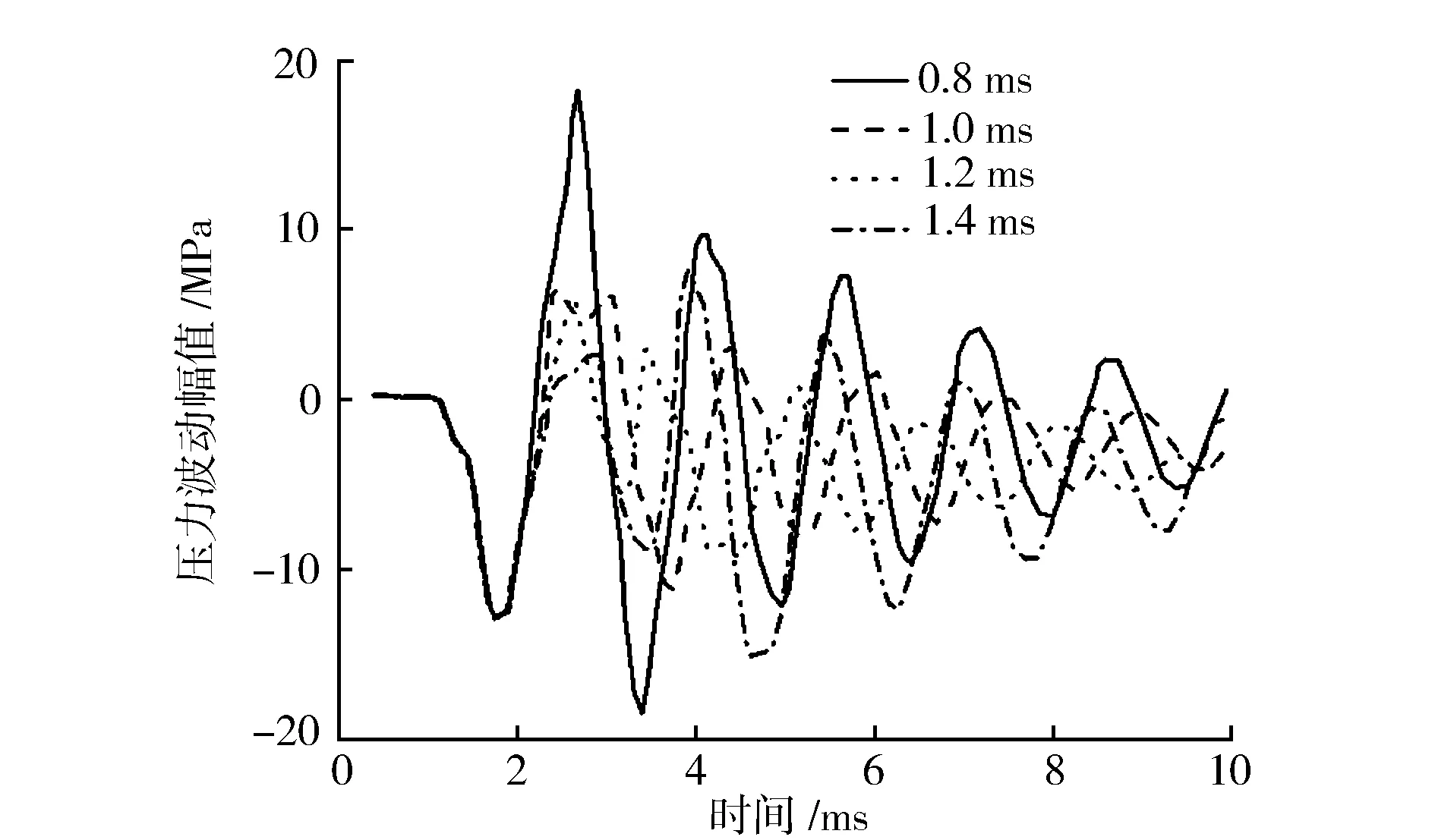
圖9 100 MPa時噴油脈寬對壓力波動的影響

在20 MPa條件下，隨著脈寬從0.8 ms上升至1.4 ms，壓力波動幅值隨之略微減小；而在100 MPa軌壓下，與圖7中60 MPa條件下的情況類似，波動幅值隨著脈寬的連續增大先減小再增大。這主要是因為在不同噴油脈寬條件下，針閥開始關閉落座時間不同。針閥的開啟和關閉會造成噴油器內蓄壓腔壓力周期性波動，同樣也會引起共軌管內的壓力產生波動，但共軌管內的壓力波動相對蓄壓腔內的油壓波動存在滯后。即如果針閥開始關閉的時刻處在蓄壓腔壓力波動幅值上升的階段，則會促進共軌管內的波動；而如果針閥開始關閉時刻處于蓄壓腔壓力波動幅值下降的階段，則會削弱共軌管內的波動，這也導致了在相同軌壓不同噴油脈寬條件下，油壓波動幅值的變化呈現出不同的變化趨勢。所以在100 MPa軌壓時，噴油脈寬從0.8 ms變化至1.4 ms過程中，由于噴油結束時間不同，油壓波動幅值出現先減小再增大的情況。

2.3 共軌管直徑對油壓波動的影響

高壓共軌系統中的共軌管直徑也會影響燃油波動規律。對比不同管徑下油壓波動的變化應在共軌管容積不變的前提下進行，否則會導致其他重要參數發生變動，不利于對單一變量進行研究。本節仿真是基于 CRS900 試驗臺共軌部件的測量數據，在此基礎上對共軌管直徑進行單一變量研究。

實測CRS900試驗臺共軌管內管徑為16 mm，長300 mm。表2列出仿真所選取的5種不同內管徑，在保持容積不變的前提下所對應的共軌管長度。

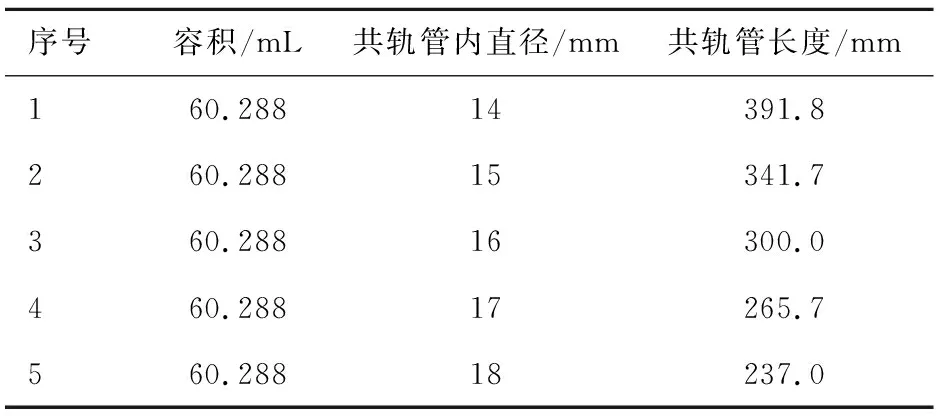
表2 仿真共軌管內管徑和長度

圖10示出在60 MPa噴油壓力，1.0 ms脈寬下，不同共軌管內直徑下管內壓力波動隨時間變化的趨勢。由圖10可知，隨著共軌管內直徑增大，油壓脈動幅值明顯減小，但由于噴油壓力和噴油脈寬是固定的，所以油壓波動頻率基本保持不變。在噴油器剛剛關閉時，受到針閥落座壓力波影響，管內產生水擊波動現象，且初次振動幅值最大。隨著噴油器關閉，共軌管內油壓逐漸趨于平穩，逐步收斂于設定的期望軌壓。在振幅隨時間遞減的過程中，大管徑所對應的各個周期內的振幅均小于小管徑對應的振幅。綜合以上分析，選擇較大的共軌管直徑有助于減小內部燃油波動的影響，但是也并非管徑越大越好，管徑過大會影響管內油壓的建立響應時間。

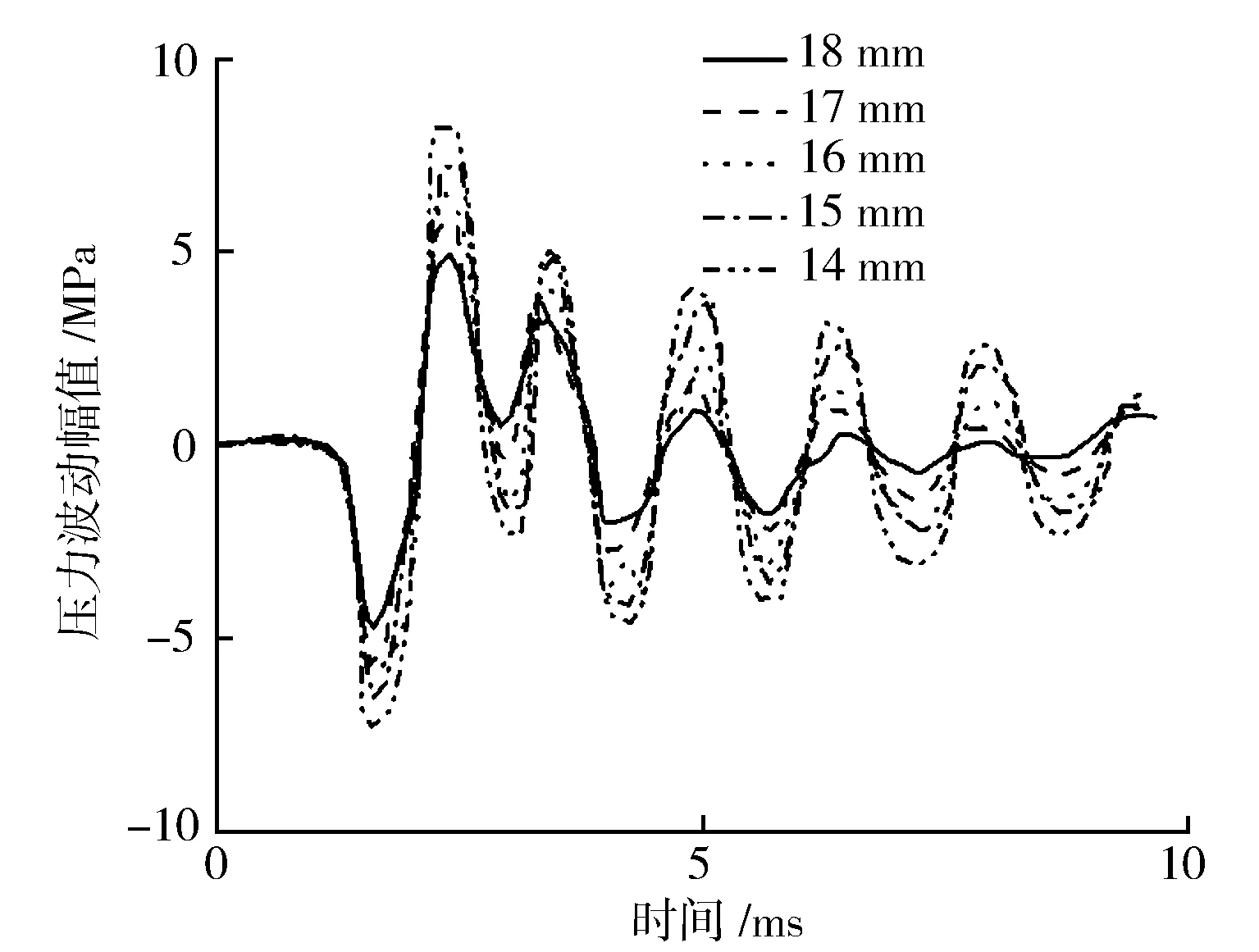
圖10 共軌管直徑對壓力波動的影響

3 基于R語言的油壓波動影響因素分析

在數據的回歸分析中，如果樣本包含兩個或以上的自變量，就應當歸結為多元線性回歸問題。針對噴油壓力、噴油脈寬、共軌管直徑3個自變量與因變量的仿真數據，回歸分析計算量較大，分析較為繁雜，本研究借助R語言環境，將不同自變量對因變量的影響轉換為標分進行回歸分析。

建立多元線性回歸模型：

yi=b0+b1x1+b2x2+b3x3+μi。

(1)

通過cor()函數求得脈寬、軌壓和共軌管管徑與波動幅度之間相關系數矩陣(見表3)。其中mk為脈寬，gy為軌壓，gj為共軌管管徑，volatility為波動幅度。

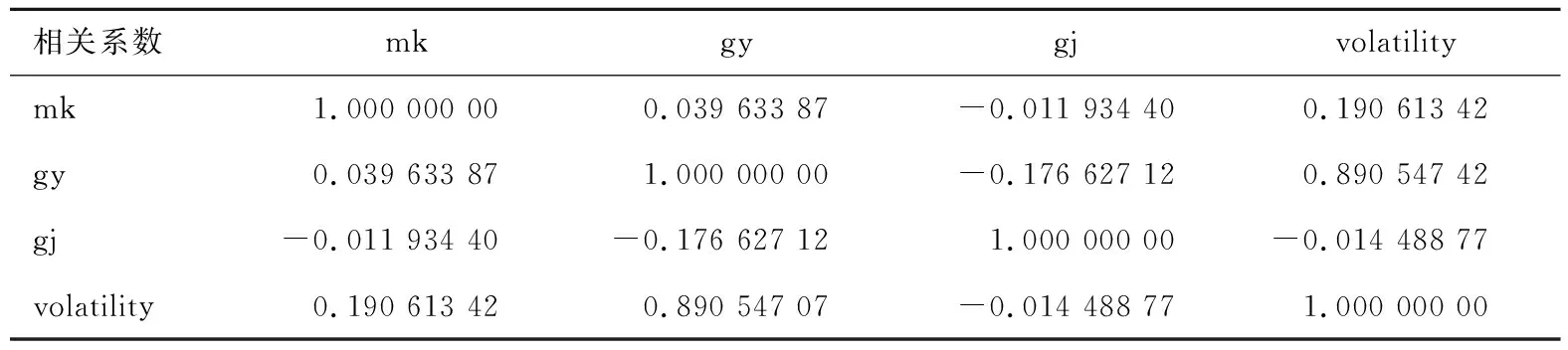
表3 cor(data1)相關系數矩陣

由該相關系數矩陣可以看出，軌壓與波動幅度相關性達到0.89，呈強相關關系，共軌管管徑與波動幅度呈現負相關，這也與仿真結果一致。

圖11示出scatterplotMatrix函數輸出的在非對角線區域變量間的散點相關矩陣圖。矩陣圖由16副小圖組成，每一幅圖顯示了自變量之間兩兩對應的關系。本研究關注3個自變量(脈寬、軌壓、管徑)與因變量油壓波動幅度之間的關系，即第4列的圖形信息。從圖11可以看出，波動幅度隨著軌壓增大而增大明顯，而隨著脈寬和共軌管管徑在仿真數據區間內變化幅度不明顯。

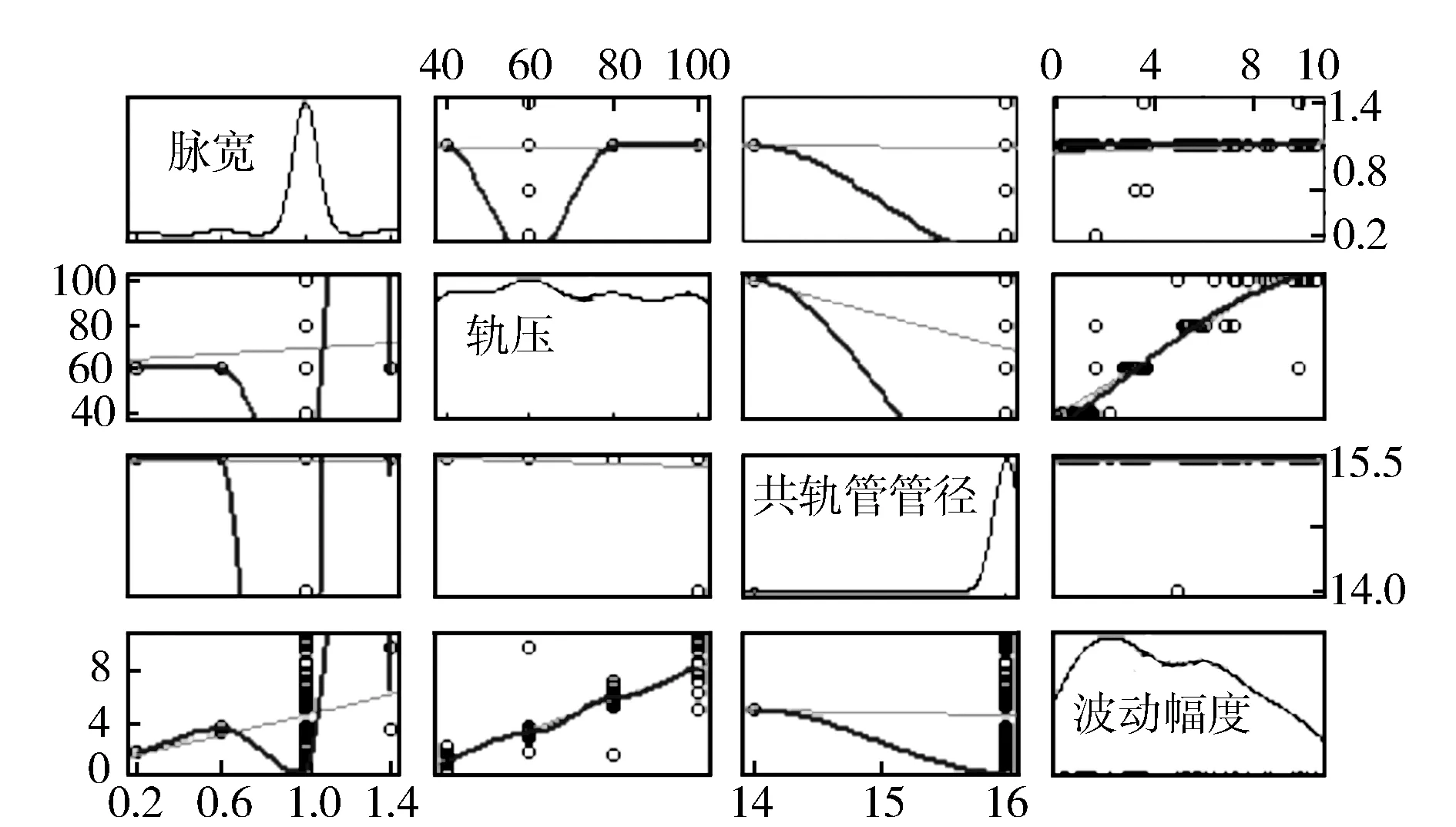
圖11 散點相關矩陣圖

在此基礎上，通過應用lm()函數擬合多元線性回歸模型，該函數輸出結果如下：

Call:

lm(formu1a～volati1ity～mk + gy + gj, data = data1)

Residua1s:

Min 1Q Median 3Q Max

-4.363 6 -0.542 5 -0.134 0 0.413 0 5.123 5

Coefficients:

Estimate Std.Error t value Pr(<|t|)

---

signif.codes: 0 '***' 0.001 '**' 0.01'*' 0.05 '.' 0.1 ' ' 1

Residua1 standard error: 1.24 on 56 degrees of freedom

Mu1tiple R-squared: 0.838 5, Adjusted R-squared: 0.829 9

F-statistic: 96.93 on 3 and 56 DF,p-value:<2.2e-16

>confint(fit)

在本例中，軌壓的回歸系數為0.12，表示控制脈寬和管徑不變時，軌壓上升1%，波動幅度將會上升0.12%，它的系數在p<0.001的水平下顯著不為0。

結果表明，軌壓改變1%，波動幅度就在95%的置信區間[0.11,0.14]中變化。

為了進一步說明各個自變量對油壓波動影響所占的權重大小，通過relweights()函數對樣本數據中各個預測變量的相對重要性進行了進一步的計算，結果見圖12。

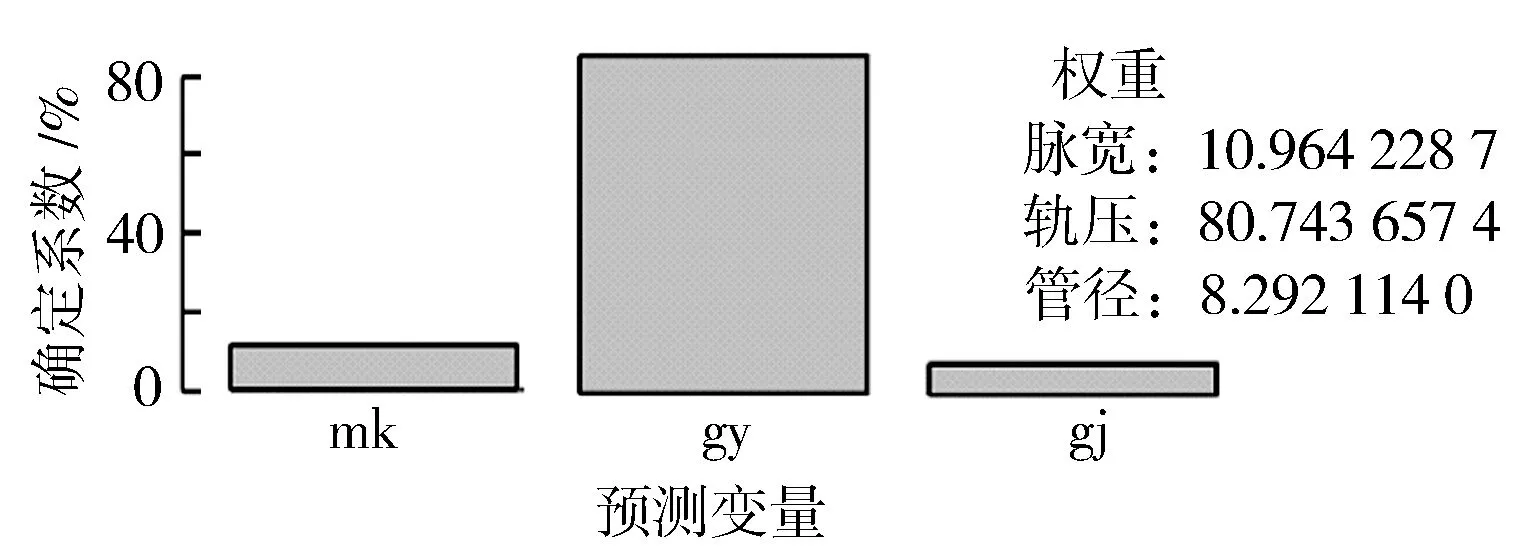
圖12 預測變量相對重要性

由圖12可以看出，在噴油壓力、噴油脈寬和共軌管管徑3個影響因素中，軌壓即噴油壓力對油壓波動幅值的影響權重高達80.74%，對油壓波動的影響占據主導地位，而脈寬和管徑影響較小，分別占據10.96%和8.29%。

4 結論

a)保持共軌管直徑和脈寬不變，共軌管內的油壓波動幅值隨著噴油壓力的增大呈現增大趨勢，且隨著軌壓增大，噴油器噴油后油壓波動頻率升高；

b)保持共軌管直徑和噴油壓力不變，不同的噴油脈寬對油壓波動幅值的影響具有不確定性，即隨著脈寬增大，波動幅值增量為正或負；

c)保持噴油壓力和脈寬不變，在保持容積不變的前提下改變共軌管直徑和長度會對管內油壓波動造成影響，共軌管直徑增大油壓脈動幅值明顯減小，但由于噴油壓力和噴油脈寬是固定的，所以油壓波動頻率基本保持不變；

d)在噴油壓力、噴油脈寬和共軌管管徑3個影響因素中，軌壓即噴油壓力對油壓波動幅值的影響權重高達80.74%，對油壓波動的影響占據主導地位。