應用有限單元法的機床進給系統軸扭特性分析

陳 曄，熊曉航，趙春雨，張義民

（1.遼寧工業大學機械工程與自動化學院，遼寧 錦州 121001；2.東北大學機械工程與自動化學院，遼寧 沈陽 110819；3.杭州電子科技大學機械工程學院，浙江 杭州 310018）

1 引言

在機床的滾珠絲杠進給系統中，工作臺和螺母與絲杠相連接，在受到工作載荷的作用時，絲杠和螺母會產生軸向和扭轉的接觸變形，從而導致絲杠產生軸向振動和扭轉振動，進而使工作臺產生軸向位移，影響進給系統的定位精度[1-2]。因此，研究機床傳動系統的動力學是提高工作臺定位精度的基礎，國內外許多學者都對此進行了大量的研究工作。文獻[3-5]對絲杠螺母結合面分別給出了有限元模型，并對動力學特性進行了分析；文獻[6-9]對進給系統應用集中質量法建模，并對系統的振動響應進行了分析；文獻[10]提出一種基于時間序列的進給系統建模方法，并用于加速度響應特性的預測；文獻[11-12]分別對傳動絲杠建立了振型方程，并對相應振型進行了分析，文獻[13]考慮了摩擦和間隙因素對滾珠絲杠進給系統建模與分析。工作臺與絲杠通過螺母接觸相連，國內外對其接觸特性與剛度進行了很多研究[14-20]，如應用Frenet-Serret坐標系研究滾珠絲杠副的動力學特性、和接觸剛度求解；對滾珠絲杠副的滾動體承載、蠕滑以及摩擦特性進行研究。基于上述學者的研究，可較為準確的求取絲杠螺母副的接觸剛度。

機床工作臺位置在工作時是沿絲杠軸向不斷變化的，這會導致機床進給系統的動態性能、固有頻率以及振動響應等均隨之發生變化，而加工過程中工作臺所受的多為變載荷，所帶來的振動問題將更為突出，將會影響加工精度。而上述文獻中，多將絲杠作為集中質量處理建立數學模型或僅僅應用有限元分析軟件建立進給系統的物理模型，影響計算；精度；同時工作臺位置對系統，特別是工作臺自身的動態特性影響的分析并未提及。因此，對于機床進給系統精細的動力學建模以及對工作臺的動態特性分析還有必要進行深入研究。

基于有限元法，以某數控車床為例，將絲杠進行單元劃分，建立考慮軸向和扭轉耦合的進給系統的動力學方程，討論了單元體數目對提高運算精度和計算時間的影響，對于機床工作臺在不同位置下影響其軸向振動模態所對應的固有頻率、工作臺動態響應進行研究，并進行了試驗驗證，證明在合理選取單元體數目的情況下該模型具有較高準確性以及運算效率。

2 基于有限元法的系統動力學方程

2.1 進給系統模型與單元體劃分

以絲杠螺母副以及工作臺刀具為研究對象，考慮軸向、扭轉變形，建立的進給單元的動力學模型，如圖1所示。

圖1 滾珠絲杠進給系統模型Fig.1 Simple Model of Ball Screw Drive System

工作臺簡化為質量為ms的質量塊，以絲杠左端為坐標原點建立坐標系，設工作臺沿z方向的位移為u s(t)，扭轉位角位移為φs(t)，絲杠螺母副沿z方向的軸向接觸剛度和阻尼分別記為k u、cu；繞z軸的扭轉剛度和阻尼記為kφ、cφ。前、后支承軸承沿z方向移動的軸向剛度和阻尼分別記為；兩軸承繞z軸轉動的扭轉剛度和阻尼分別記為

由于絲杠為連續體，其振型函數和運動方程應是關于時間t和空間z的函數，應用有限元法，將絲杠劃分為n個單元體，圖2所示為絲杠第i個單元體（i=1，2…n），其中，節點i和節點i+1上沿z方向的位移分別為u i(t)和u i+1(t)，繞z軸扭轉的角位移分別為φi(t)和φi+1(t)。設單元廣義坐標自由度順序為：

圖2 絲杠單元體Fig.2 Element of Screw

對節點單元應用Lagrange方程，得到單元i的質量矩陣m i和剛度矩陣k i，i=2，3，…，n-1。

式中：ρ—絲杠密度；l為絲杠單元長度；A—絲杠截面積；E—絲杠的彈性模量；I—絲杠截面極慣性矩；J—絲杠截面中性軸極慣性矩；G—剪切彈性模量。

2.2 特殊單元

同時，考慮特殊單元體：和左右軸承接觸的兩個邊界單元，以及與工作臺螺母接觸的單元體，并分別求出其各自的質量矩陣和剛度矩陣以及相關耦合項。

（1）與左右軸承接觸的邊界單元

邊界單元的質量矩陣與中間單元的相同，即：

以左側邊界單元為例，如圖3所示。對節點單元應用La?grange方程，可得其單元剛度矩陣：

圖3 絲杠邊界單元體Fig.3 Boundary Element of Screw

同理，可得到右側單元的剛度矩陣：

（2）與工作臺連接的第j個絲杠單元

設絲杠第j個節點與螺母工作臺接觸，如圖4所示，節點j和節點j+1上沿z方向的位移分別為u j(t)和u j+1(t)，繞z軸扭轉的角位移分別為。計算工作臺的動能：

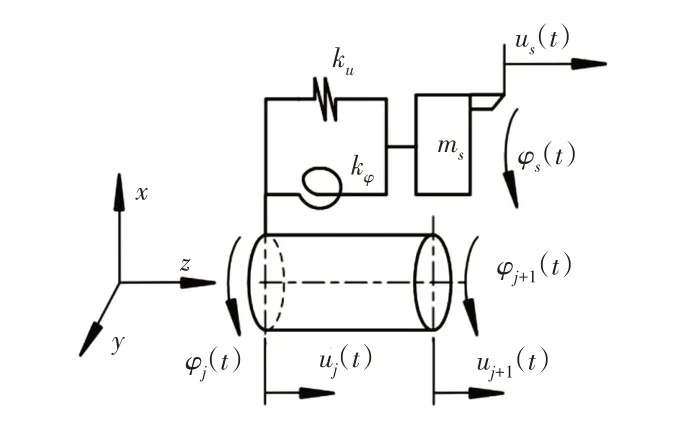
圖4 工作臺與絲杠單元體Fig.4 The Worktable and Screw Element

由式（7）可知，絲杠單元體j的質量矩陣中不存在與工作臺質量的耦合。

計算工作臺的勢能：

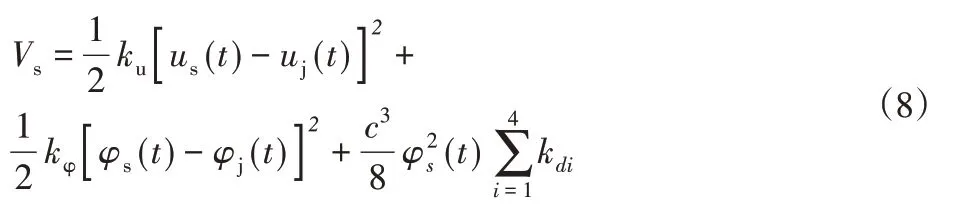
將V s分別對u j、φj、u s和φs求偏導，得：

從上式可以看出，第j個絲杠單元剛度矩陣中存在關于u s和φs的耦合項。

2.3 單元組集

絲杠單元體的單元質量矩陣和剛度矩陣按絲杠位移向量通過矩陣變換（式（10）），可得到絲杠的質量和剛度矩陣。

式中：A i—變換矩陣。

考慮工作臺軸向位移的自由度，整個系統的自由度為：

2.4 進給系統動力學方程

結合絲杠的質量矩陣和剛度矩陣以及相關耦合項，可得系統的質量和剛度矩陣，進而求得進給系統運動微分方程為：

式中：M—系統質量矩陣；K—系統剛度矩陣；F—激勵向量；q—系統廣義坐標。

這里研究的對象為典型的數控車床z軸進給系統，其相關的參數，如表1所示。

表1 進給系統的參數Tab.1 Technical Data of Feed Drive System

3 機床工作臺動態特性分析

令F=0，方程（3）的特征方程為：

由方程（13）可求解出系統的所有固有頻率和固有振型，振動系統的固有頻率數目與系統自由度數目相同，由于這里系統的動力學方程是基于有限單元法建立，故系統的固有頻率數目眾多，由于篇幅關系，這里只研究對系統影響較大的前3階固有頻率進行分析。由于絲杠單元體n的數目影響方程的運算精度和運算效率，數目過少運算速度快但精度低，數目過高則反之，故取不同單元體試算z∕L=0.5處的前3階固有頻率，發現當n取120以上時，前三階固有頻率值均趨于穩定收斂，而當n超過90之后，由于迭代次數增多，程序運行的時間損耗也大幅度提高。故綜合考慮運算精度和速度這里仿真運算中均取絲杠單元體數目n=120。

取工作臺位置為z∕L=0.5處，應用MATLAB求解方程（13），得到系統的前3階固有頻率及其對應的模態，如表2所示。由表2可以看出，工作臺軸向振動模態所對應的是系統的第1、3階固有頻率。

表2 z/L=0.5時系統前3階固有頻率Tab.2 The First 3 Natural Frequencies as z/L=0.5

但機床在工作時，工作臺位置并非是固定不變的，這也就意味著在動力學方程（3）中，與工作臺發生耦合的絲杠單元是不斷變化的，故在工作過程中系統為時變系統，其質量矩陣和剛度矩陣均會因為工作臺位置變化而發生變化，進而系統的固有特性也會發變化。工作臺位置在z∕L=0.1～0.9范圍內變化時，影響工作臺軸向振動模態的系統第1、3階固有頻率的變化規律，如圖5所示。從圖5（a）中可以看出，系統的第1階固有頻率呈現先減后增的變化趨勢，其中固有頻率最大的工作臺位置出現在絲杠z∕L=0.1和0.9處，即絲杠端部；而固有頻率最大的工作臺位置出現在絲杠z∕L=0.5處，即絲杠中部處，固有頻率的變化率達到了50.58%。

從圖5（b）中可以看出，系統的第2階固有頻率只在工作臺處于兩端處突然呈現較大的變化，變化率為8.48%，而沿絲杠其他位置處基本保持不變。由于工作時，工作臺位置不會達到兩端部，故可以認為工作臺在z軸位置變化對系統的第2階固有頻率影響不大。

從圖5（c）中可見，系統的第3階固有頻率的變化趨勢與第1階恰好相反，呈現先增大后減小的變化規律，其中固有頻率最大的工作臺位置均出現在絲杠z∕L=0.5處，而固有頻率最小的工作臺位置亦都出現在絲杠z∕L=0.1和0.9處。固有頻率的變化率為10.3 %。

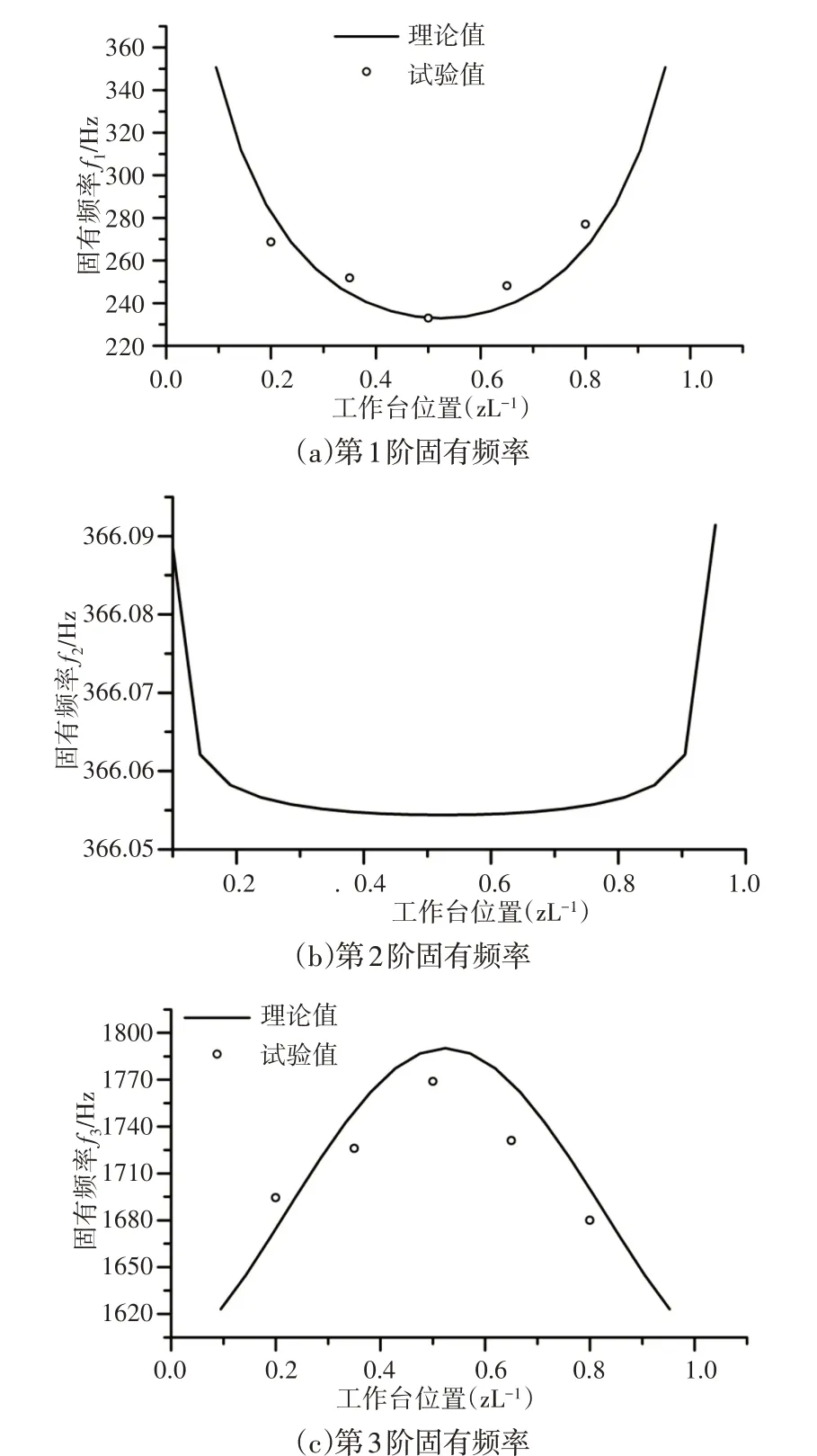
圖5 系統前3階固有頻率隨工作臺位置的變化規律Fig.5 Variation of the First Three Natural Frequencies with Positions of Worktable

4 試驗驗證

為驗證這一規律，這里采用一臺典型的數控車床作為試驗對象，采用錘擊法對機床工作臺特殊點進行了動態特性試驗，如圖6所示。

圖6 試驗系統Fig.6 Experiment System

為使測試更加準確，應用086M92ES型電子沖擊力錘，可提供可重復的穩定沖擊力，并在工作臺的關鍵點處布置壓電式加速度傳感器的測振點，加速度傳感器主要拾取在敲擊點處施加沿z軸的脈沖激勵后工作臺的速度振動響應信號，經過濾波、快速傅里葉變換等處理，便可以得到工作臺在頻域上的速度振動響應。試驗選取工作臺處在z∕L=0.2、z∕L=0.35、z∕L=0.5、z∕L=0.65以及z∕L=0.8五個位置作為試驗點，拾取速度響應信號。通過測試得到的頻率成分，發現在有兩個明顯的頻率分別與理論解中的第1和3階固有頻率相對應，因此將測試值與理論值一起繪出，如圖5a、c所示，第1階固有頻率的仿真結果與試驗的誤差在4.5%以內，第3階固有頻率的仿真結果與試驗結果的誤差在2%以內，且變化趨勢與仿真計算得出的結論相吻合。由此可見，這里的進給系統動力學方程在求解系統固有頻率，特別是求系統中、低段固有頻率時均具有較高的精度。

5 結論

（1）應用有限元法，將絲杠作為連續體劃分單元體，建立機床進給系統軸向和扭轉振動的動力學方程，可求解系統、特別是絲杠連續體各個位置處的動態特性。通過討論單元體數目對提高運算精度和計算時間的影響，得到當絲杠單元體數目取120時，系統前三階固有頻率的仿真結果均趨于穩定收斂，此時仿真結果與試驗結果的誤差低于4.5%。（2）軸向振動模態頻率隨工作臺位置呈現非線性的變化規律：第1階固有頻率呈現先減后增的變化趨勢，其中固有頻率最大的工作臺位置出現在絲杠端部；第3階固有頻率則為先增后減的變化規律，其中固有頻率最大的工作臺位置均出現在絲杠中部。第2階固有頻率受工作臺位置的影響并不顯著。