CDZ350鉆桿吊卡吊耳彈塑性分析和殘余應力研究

周井玲，李 昕，許波兵，王新鵬

（1.南通大學機械工程學院，江蘇 南通 226019；2.江蘇如東通用石油機械股份有限公司，江蘇 南通 226499）

1 引言

隨著科技水平的進步，我國石油開采作業從陸地逐漸轉移到海洋，深度也從近海的200m提升至深海3000m。深海石油開采的實現得益于高自動化、高安全性、高穩定性的開采設備和開采平臺。吊卡作為鉆井設備中最為常用的一種，其穩定性、安全性對于海洋鉆井和石油開采是極其重要的。吊卡工作時，由兩側的吊環勾住吊卡每一側的吊耳，帶動中央錐面上夾持的管柱，進行平穩的提升運動。吊耳和吊環的接觸是高副接觸，局部接觸應力很大。高的接觸應力會在吊耳表面下方產生高等效應力場[1-2]，次表面可能會產生塑性屈服[3]。在工程結構設計中，允許結構產生一定塑性變形又不導致結構破壞[6]，可充分發揮材料的潛能，提高承載能力。研究吊耳下方的塑性變形對優化吊耳設計，檢驗其安全性具有重要意義。

國內對吊耳接觸的研究大多數基于彈性理論：尚福林[1]等采用理論計算和有限元得到了CD吊卡吊耳接觸表面應力和裂紋應力強度因子，基于彈性理論對吊卡吊耳安全性進行了了評判；文獻[2]對套管吊卡進行了有限元仿真，依據彈性理論對套管吊卡進行了穩定性校核和裂紋擴展研究。由于接觸行為通常伴有較大的應力，較易產生塑性變形，僅進行彈性范圍的研究不能充分發揮材料的性能，故對吊卡吊耳接觸研究應采用彈塑性理論。對彈塑性問題的研究國內外均以數值方法為主：文獻[9]采用了一種數值算法計算了彈塑性接觸，并提出了一種計算方法優化，大大節省了計算資源；何濤[7]等運用了Wang的方法，對彈塑性有潤滑點接觸問題進形了求解，得到了加載卸載的應力和殘余應力分布，以及不同滾動速率下油膜的厚度。

現以CDZ350型吊卡為研究對象，建立吊耳-吊環的接觸模型，采用有限元數值計算方法[2，4]，對吊卡承受1.5倍額定載荷時吊耳的彈塑性變形、卸載后殘余應力和殘余應力對二次加載的影響進行研究，模擬了吊卡產品出廠時進行的1.5倍壓力試驗-卸載-正常使用的過程。為證明有限元計算的準確性，對吊卡吊耳側面進行貼片驗證。研究結果為吊卡的材料工藝設計、安全性設計提供了理論依據。

2 材料塑性性質

2.1 吊耳材料塑性變形曲線

金屬材料在受到超過屈服極限的應力時會發生塑性變形[6]。為了表示材料塑性變形的性質，通常都要對其進行常溫單軸拉伸試驗。吊卡主體的材料為35CrMoV，經過油淬之后表面以及表層以下會有一層淬透層，深度約為50mm。根據《GB∕T 228.1-2010金屬材料室溫拉伸試驗方法》，對取自吊卡吊耳部位淬透層直徑為10mm的樣件進行了單軸拉伸試驗[4]，得到了淬火強化后的35CrMov的單軸拉伸曲線。35CrMoV單軸拉伸曲線，如圖1所示。

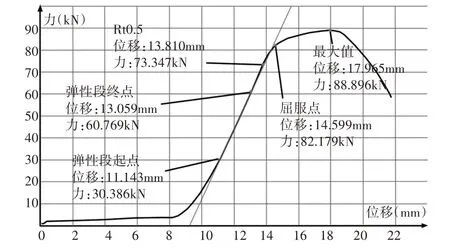
圖1 35CrMoV單軸拉伸曲線Fig.1 Uniaxial Tension Curve of 35CrMoV

得到單軸拉伸曲線后將拉力除以試件的截面積可以得到應力[6]，可以計算出抗拉極限、屈服極限等力學參數，計算結果，如表1所示。

表1 35CrMoV力學性能參數（MPa）Tab.1 Mechanical Properties of 35CrMoV（MPa）

由圖1可發現35CrMoV的單軸拉伸曲線中未表現有明顯的屈服平臺，也沒有明顯的上下屈服極限之分，可采用線性硬化材料的模型對材料的性質進行定義。在線性硬化模型中[6-8]，任意一點應力應變關系可以表示為：

式中：E—彈性模量；

Et—切線模量；

σs—屈服強度；

σ—該點的應力；

ε—該點的應變。

將35CrMoV的力學參數測試結果帶入式（1）即可求得線性硬化模型的剪切模量。計算后可得35CrMoV材料的切線模量為3768.5MPa。同時圖1中材料在超過抗拉極限后隨應變增加應力減小，此時材料發生了軟化現象，材料性能下降。在接觸問題中，如果接觸體表面材料達到塑性軟化狀態就會發生塑性擠出和塑性流動，造成材料破壞。

3 彈塑性接觸有限元分析

3.1 吊卡吊耳接觸有限元模型

以CDZ350型吊卡吊耳和吊環接觸為原型，根據圣維南原理和對稱性，截取吊耳部分，簡化吊耳吊環接觸模型，如圖2所示。網格劃分時全采用精度高的六面體單元，并在接觸面添加接觸面網格細化，使計算結果更加精確。

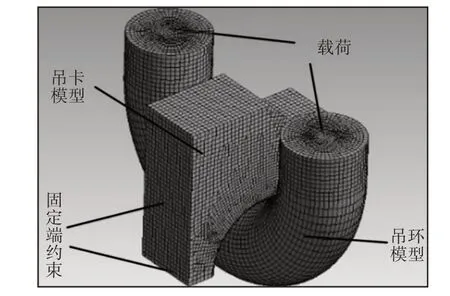
圖2 吊耳吊環簡化模型和網格劃分Fig.2 Simplified Model and Hex-Meshing of Lifting Lug and Ring

網格模型單元數為119311，節點數為463845。設定吊耳吊環接觸對為無摩擦，接觸計算方式為增廣拉格朗日法。為了模擬吊卡的實際工作情況[5]，在截取出的吊耳模型的兩個截取截面添加固定端約束，在吊環模型的頂面施加向上的載荷。為了模擬1.5倍試壓-卸載-正常使用的而過程，載荷設置時分為四步，對應載荷值設置為1.5倍額定載荷、無載荷、1倍額定載荷、無載荷。

3.2 彈塑性分析和殘余應力有限元分析結果

將材料的彈性模量、切線模量、泊松比等材料塑性系數導入到ANSYS Workbench中，進行有限元計算。建立分析坐標系，原點位于初始接觸點，方向如圖3所示。

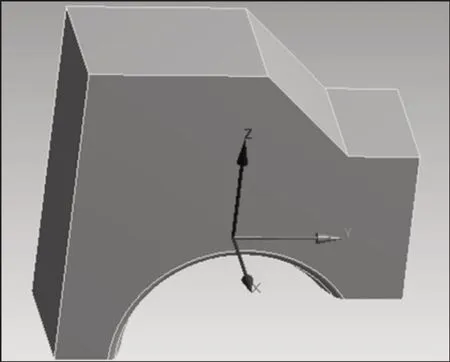
圖3吊耳分析坐標系Fig.3 Lifting Lug Analysis Coordinate System

圖4 ～圖7分別為yoz面上的1.5倍載荷、一次卸載、1倍載荷、二次卸載情況下的吊耳次表面等效應力圖。可以看出在1.5倍載荷時，吊耳次表面發生了小范圍的塑性變形，塑性區y向長度約為33mm，z方向長度約為26mm。形狀較為不規則，且塑性區擴展到了表面。

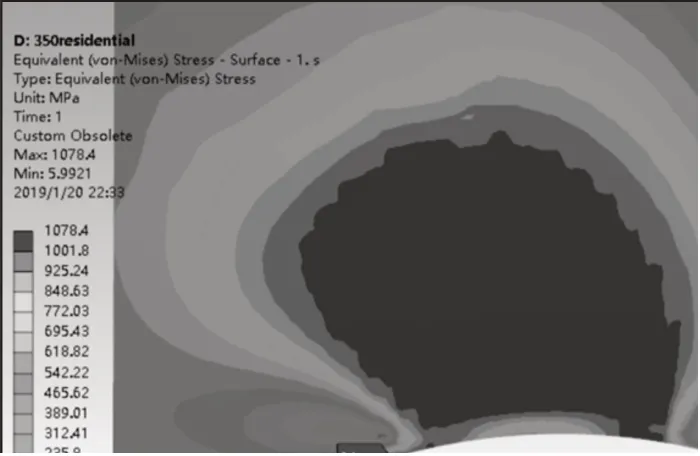
圖4 1.5倍額定載荷y oz面等效應力Fig.4 Equivalent Stress on y o z Surface under 1.5 Time Rated Load

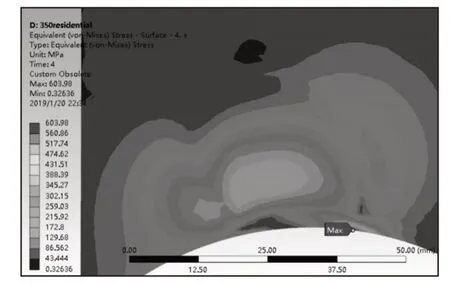
圖7 二次卸載殘余應力Fig.7 Residual Stress of Secondary Unloading

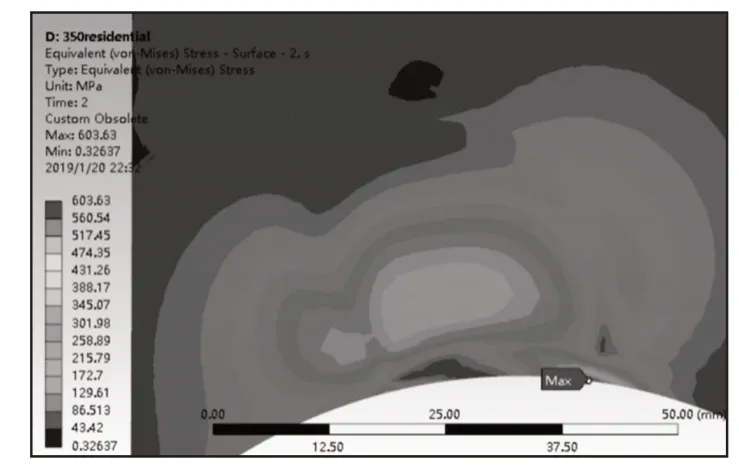
圖5 一次卸載殘余應力Fig.5 Residual Stress of Primary Unloading

通過圖4～圖7可以看出在兩次的加載-卸載過程中yoz截面上接觸區次表面等效應力分布規律主要有：

（1）1.5倍一次加載時接觸區次表面存在塑性區，塑性區中應力分布平緩，且兩端延伸到表面。最高應力為1078MPa，超過屈服極限，發生塑性變形，但未超過材料抗拉極限，說明材料僅發生硬化而沒有發生軟化現象，不會發生塑性擠出和塑性流動等接觸塑性破壞。

（2）兩次卸載后殘余應力分布相似，達到穩定狀態[10]。內部次表面殘余應力存在峰值，大小為443.7MPa。表面殘余應力最高為603.98MPa，出現在加載時表面塑性變形處。殘余應力分布區域基本為加載時的塑性區域，并且在彈性區和塑性區邊界存在兩個應力低峰[7，9]。

（3）二次加載時最高應力為1005.6MPa，未超過屈服極限，并且圖6中左側應力較圖4中減小，可認為殘余應力具有一定的保護作用，能夠減小正常使用中次表面應力，提高承載能力。

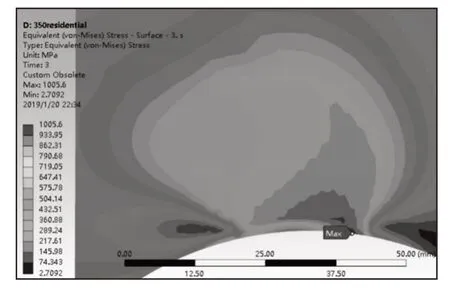
圖6 二次加載等效應力Fig.6 Equivalent Stress of Secondary Loading

4 吊卡吊耳貼片測試

4.1 實驗對象和試驗設備

對吊耳表面貼應變片測量應變可驗證有限元結果。采用PA120-5A型應變片以及YJ-25型應變測試儀，由千噸級壓力試驗機提供壓力，測量CDZ350吊卡在1.5倍額定載荷下和卸載后吊耳側面的應變情況，與有限元結果進行對比。由于應變片工作時需排除外界的干擾，所以布置位置只能位于吊耳側面。吊耳側面貼片位置和壓力測試工裝圖，如圖8、圖9所示。1-3號點、4號點、5號點與水平面分別呈90°、60°、30°夾角，1-3號點之間間隔為20mm。

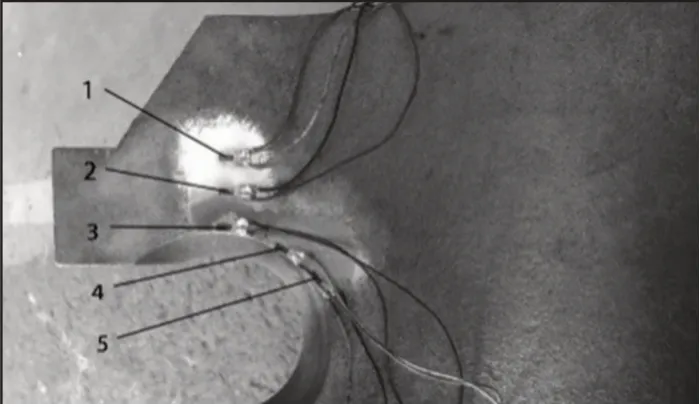
圖8 吊耳貼片位置圖Fig.8 Strain Gauge Location of Lifting Lugs

圖9 壓力測試工裝Fig.9 Pressure Test Fixture

4.2 貼片測試結果

記錄應變儀上的讀數，將讀數處以材料的彈性模量可以得到貼片方向的測試應力。提取有限元分析中表面各個測點處的各向應力數值，根據HooKe定律[3，6]

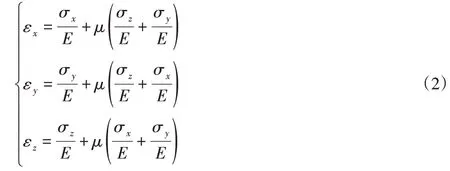
將三向應力合成為貼片方向的測試應變和應力，并將應力結果整理之下表2中。可以看到4號點在加載時應力最大，而卸載時殘余應力較小。這點和文獻[5]中的結果相一致。而1號點加載和卸載時都存在較大的應力，說明塑性區主要集中在與水平面呈90°的接觸區表面和次表面。比較有限元和實驗結果可以看兩者較為貼合，最大誤差僅為7.5%，從而驗證了有限元模擬的準確性。

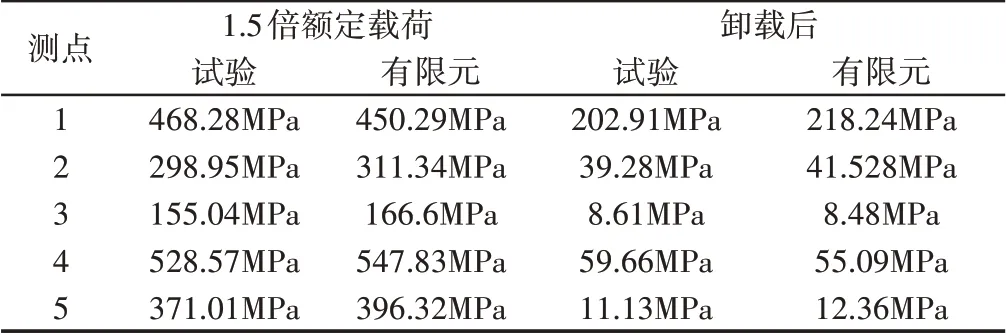
表2 各測點應力實驗值和有限元比較Tab.2 Comparison of Strain Gauge Experiment and FEM Values at Different Measuring Points

5 結論

經過上述分析可總結以下幾點：

（1）吊耳在1.5倍額定載荷下次表面和表面發生塑性變形，等效應力峰值為1078MPa，高于屈服極限低于抗拉極限，材料發生硬化，不會發生塑性破壞，可安全使用。

（2）兩次卸載后殘余應力相似，達到穩定狀態。次表面殘余應力峰值為443.7MPa，表面殘余應力峰值為603.98MPa，殘余應力主要分布區域為加載時的塑性變形區域。

（3）二次加載時等效應力峰值為1005.6MPa，未超過屈服極限，說明二次加載接觸為全彈性，內部殘余應力減小了次表面二次加載時的應力，對二次加載有保護作用。

（4）吊耳側面加載時最大殘余應力出現在1號點附近，說明塑性變形主要出現在在與水平面呈90°的接觸區表面和次表面。貼片試驗結果和有限元結果近似，最大誤差為7.5%，驗證了有限元結果的正確性。