局部魯棒主成分分析及其在故障診斷中的應用

蘇立鵬，金樟民，尤 戈，易燦燦

（1.溫州市特種設備檢測研究院，浙江 溫州 325000；2.武漢科技大學，湖北 武漢 430081）

1 引言

機械設備是國民經濟建設的重要基礎設備，廣泛應用于冶金、石油化工、電力建筑等國民經濟命脈領域[1]。機械設備一旦出現故障將會導致企業停工和嚴重的經濟損失，因此，針對機械設備可能出現的故障的診斷和結構健康監測技術在近幾十年迅速發展。而作為機械設備中起支撐作用的關鍵零部件，軸承的工作狀態將直接影響整個設備的運行狀態，因此實現對軸承的故障診斷具有重要的研究價值[2]。實測的軸承故障振動信號由于背景噪聲和外界環境干擾的存在表現出很強的非線性、非平穩特性，且有用的早期微弱故障特征極易淹沒在強噪聲背景中，因此設備故障診斷的一個重要的研究方向是故障特征的有效提取。學者提出了多種振動信號的特征提取方法。小波分解（Wavelet Trans?form，WT）[3]能將信號分解為代表信號特征成分的低頻成分和代表噪聲成分的高頻成分，但是小波基函數和分解層數的選擇對分解的結果有決定性影響。奇異譜分析（Singular Spectral Analysis，SSA）[4-5]可以將信號分解為奇異值表示的特征子空間，有用的信號特征可以通過有效的奇異值能量來評估，但是奇異值的選取仍是一個難題。

在SSA的基礎上，學者提出了低秩矩陣逼近（Low-Rank Ma?trix Approximation，LRMA）[6]的思想，在信號降噪領域稱為魯棒主成分分析方法（Robust Principal Component Analysis，RPCA）[7]，該方法假設原始信號矩陣可以分解為代表信號特征信息的低秩成分和代表噪聲的稀疏成分[8]。并將SSA中奇異值的選擇這一NP難題轉化求解奇異值之和最小化這一凸優化問題，從而有效的提取含噪信號中的特征成分。該方法的核心思想是特征成分矩陣具有全局低秩屬性，從而使得其奇異值分解的奇異值之和也較小。然而，實測的機械設備故障信號的特征成分形成的特征矩陣一般并不具有全局低秩的特性，因而RPCA可能并不適用。針對這個問題提出了局部魯棒主成分分析（Local Robust Principal Component Analysis，LRPCA）的降噪方法，與RPCA全局低秩的強條件假設不同，LRPC只需數據矩陣在有限個局部區域滿足低秩假設，并在這些區域分別構建特征成分的局部低秩近似矩陣，接著通過這些低秩矩陣的平滑凸組合來全局近似特征信號矩陣，從而實現信號的特征提取目的。該方法首先通過相空間重構[9]構建實測的一維信號的吸引子軌道矩陣，然后通過提出的局部低秩模型提取信號的故障特征成分，最后分別通過數值仿真實驗和實測的軸承外圈故障數據的分析證明提出的方法具有較好的特征提取效果。

2 理論描述

2.1 實測一維振動信號的相空間重構

由于機械故障信號有很強的非線性、非平穩特性，其在一維空間難以展示，而通過相空間重構將實測的一維振動數據轉換為吸引子矩陣，可以很好的反映原系統的許多動力學特征。在這一過程中，一維振動信號x∈[x1，…，x N]∈R N被重構為一個吸引子軌道矩陣X∈R L×K（延遲時間為1，嵌入維度為L，K=N+1-L），如式（1）所示。

2.2 魯棒主成分分析

傳統的SSA方法是對軌道矩陣進行奇異值分解X=UΛV T，利用奇異值譜的特性來提取信號的特征信息。其中U∈R L×r，V∈R K×r分別稱為左右奇異向量，Λ=diag(σ1，σ2，…，σr)是按大小順序排列的對角奇異值矩陣，則原始信號矩陣可以表示為r個奇異值表示的信號子空間的和，即，在信號降噪領域，有用的信號特征是按照奇異值譜的能量的大小（一般是前幾階奇異值）選擇特定的幾個特征子空間來表示。但是奇異值的選擇是一個亟待解決的NP難題。

針對這個問題學者提出了LRMA的思想，將奇異值的選擇問題轉化為奇異值之和的最小化的凸優化問題，而在信號降噪領域便是著名的RPCA方法。該方法假設原始信號矩陣X可以表示為代表信號特征信號的低秩成分L∈R L×K和代表噪聲成分的稀疏成分S∈R L×K的和，而低秩約束通過核范數最小化（即奇異值之和最小）來實現。該方法將SSA中奇異值的選取問題轉化為了數學上可求解的低秩成分的核范數最小化問題[10]，如式（2）所示。

2.3 局部魯棒主成分分析

由于實測的機械設備故障信號動力學特性比較復雜，其吸引子特征矩陣并不具有全局低秩的屬性。針對這個問題，可以假設數據矩陣在特定的錨點局部區域內滿足低秩的屬性，即在RP?CA的基礎上，將全局低秩強條件假設放松到矩陣局部區域低秩假設弱條件，并在這些局部區域構建對應的原始特征矩陣的低秩特征矩陣，然后通過這些低秩矩陣的平滑凸組合來全局近似特征信號矩陣，從而實現信號的故障特征提取，將該方法稱為局部魯棒主成分分析方法（LRPCA）。

隨機選擇矩陣中的q個元素錨點，并在這些錨點的局部區域構建信號特征矩陣的低秩近似矩陣L s i∈R L×K，該矩陣能精確的估計在原始特征矩陣對應的錨點s i局部區域的元素值，如圖1所示。根據RPCA的思想，可以通過構建的凸優化問題來提取對應錨點的低秩特征成分矩陣，如式（3）所示。

圖1 局部低秩矩陣近似從矩陣元素到矩陣的映射Fig.1 The Local Low-Rank Matrix Approximation Assumes an Operator that Maps Matrix Entries to Matrices

式中：d((a i，b i)，(i，j))—兩元素點(a i，b i)和(i，j)的距離函數，其值越小表示兩點之間越緊密，即通過錨點q i近似得到的低秩矩陣L i（即T(s i)）在(i，j)位置的估計值較為精確，這里我們采用反余弦函數來定義，如式（5）所示。同時K h((a i，b i)，(i，j))也轉化為K h((a i，i)K h(b i，j))的乘積形式。

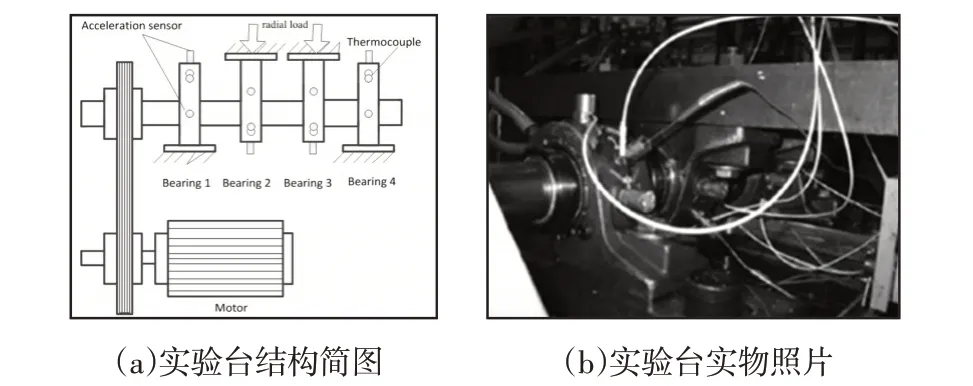
通過式（3）的求解，我們可以獲得隨機選擇的q個錨點附近區域對應的特征成分矩陣的低秩近似矩陣，可以看出每一個低秩矩陣L s i在其對應的錨點附近d(q i，·)

表1 LRPCA算法Tab.1 LRPCA Agorithm

3仿真信號分析

軸承作為機械設備中起承載作用的關鍵零部件，其故障信號通常含有調制特性，且故障特征容易被強背景噪聲所淹沒。為了證明提出方法對故障特征進行識別的效果，構建模擬數值仿真信號，如式（7）所示。

式中：x1(t)—中心頻率為f1=100Hz，調制轉頻為f r=30Hz的調制信號；x1(t)—中心頻率為f2=200Hz的簡諧信號；n(t)—水平為0.5的高斯白噪聲，采樣頻率和采樣點分別為8000Hz和8000。原始不含噪信號時域和頻域圖，如圖2（a）、圖2（b）所示。原始含噪信號時域和頻域圖，如圖2（c）、圖2（d）所示。

圖2仿真信號Fig.2 Simulation Signal

圖中：（a）、（b）—原始不含噪信號時域和頻域；（c）、（d）—原始含噪信號時域和頻域

從含噪信號的頻域圖中雖然可以看見調制信號和簡諧信號的中心頻率，但是調制信號的重要特征即調制邊頻成分被噪聲所淹沒，不易識別。采用提出的LRPCA方法對該信號進行處理，并將WT和RPCA作為對比分析方法。

WT和RPCA分析的結果分別，如圖3、圖4所示。在WT中，我們選用db8小波母函數，分解層數為4，從圖3（b）中雖然可以找到調制邊頻成分（f1±f r），但是極不容易被識別，背景噪聲的干擾依然較強。從RPCA分解結果的頻域圖中可以發現調制邊頻成分（f1±f r）被錯誤地作為無關信號而濾波掉，而且背景噪聲成分仍然存在。

圖3 WT提取的結果Fig.3 The Feature Extraction Result by The WT method

圖4 RPCA提取的結果Fig.4 The Feature Extraction Result by The RPCA Method

使用提出的LRPCA方法處理仿真信號，其重構回的一維特征成分時頻域，如圖5所示。可以發現調制邊頻成分（f1±f r）清晰可見，且噪聲的水平已經降到了非常低的水平，對于特征成分的識別幾乎沒有影響，因此，提出的方法的降噪效果和特征提取的結果非常有效，且明顯優于其他兩種分析方法。

圖5提出的方法的提取結果Fig.5 The Feature Extraction Result by The Proposed Method

4實測信號分析

為了進一步驗證提出方法的實用性，我們對美國辛辛那提大學軸承故障實驗臺采集的軸承外圈故障數據進行了分析。實驗裝置，如圖6所示。在主軸上有四個雙列圓錐滾子軸承，每個有16個滾動體，滾子直徑為d=3.31mm，軸承中徑為D=28.15mm，壓力角為α=15.17°，轉頻為fr=33.33Hz，采樣頻率和采樣點數分別為20000Hz和20000。理論外圈故障理論頻率為：f0=235.29Hz。原始信號的時域和頻域圖，如圖7所示。由于噪聲和其他干擾頻率（圖中紅色圓圈所示）的存在，導致故障特征成分難以識別。

圖6軸承故障實驗臺Fig.6 Rolling Bearing Test Table

圖7軸承外圈故障信號Fig.7 Rolling Bearing Outer Ring Fault Signal

使用提出的方法對該信號進行處理，并選擇WT和RPCA方法作為對比分析。WT和RPCA的分析結果分別，如圖8、圖9所示。在WT中，雖然可以找到故障特征頻率的二階諧波頻率，但是噪聲的干擾依然很大，故障仍難以準確定位。而在RPCA中，干擾頻率成分依然較多，對故障的判斷造成一定的影響。因此WT和RPCA的故障特征提取效果有限。

圖9通過RPCA處理后的提取信號頻域Fig.9 The Extracted Signal in Frequency Domain by RPCA

提出的方法的特征提取結果，如圖10所示。從圖中很容易的識別外圈故障頻率f o和其二階諧波頻率2f o以及轉頻f r，且背景噪聲水平降到了很低的水平，故障特征清晰可見。綜上，分析結果表明，提出的方法對于實測的州城外圈故障有很好的特征提取效果，且相較于其他兩種方法，其性能明顯更加優越。

圖10通過提出的方法處理后的恢復信號頻域Fig.10 The Extracted Signal by The Proposed Method in Frequency Domain

5結論

一種新的局部魯棒主成分分析的方法被提出并用于機械設備故障信號的降噪和特征提取，該方法在魯棒主成分分析的基礎上，將數據矩陣全局低秩的強條件假設放松到局部低秩條件，這個條件與實際的故障特征矩陣矩陣更加吻合。

首先在相空間重構得到的吸引子數據矩陣元素中隨機的選取有限個錨點，并在錨點附近區域通過低秩逼近構建待提取特征矩陣的近似矩陣，然后通過平滑凸組合這些局部低秩矩陣為特征矩陣的全局近似矩陣，再將得到的矩陣通過相空間重構逆過程即為提取的信號的特征成分。分別通過數值仿真實驗和實測軸承外圈故障數據的分析，結果表明提出的方法具有很好的降噪和特征提取效果。