微通道內(nèi)低黏聚合物流體的停留時間分布研究
趙晶,李伯耿,卜志揚(yáng),范宏
(化學(xué)工程聯(lián)合國家重點(diǎn)實(shí)驗(yàn)室,浙江大學(xué)化學(xué)工程與生物工程學(xué)院,浙江杭州 310027)
引 言
連續(xù)流動反應(yīng)器內(nèi)物料的停留時間分布(RTD),對小分子化學(xué)反應(yīng)的影響主要體現(xiàn)在反應(yīng)速率(即反應(yīng)器出口的轉(zhuǎn)化率)。對合成高分子反應(yīng)而言,更涉及聚合產(chǎn)物的分子量分布(MWD)和共聚組成分布。因而,很大程度上影響到聚合物產(chǎn)品的性能。如聚合反應(yīng)呈活性聚合或逐步聚合機(jī)理時,聚合產(chǎn)物的分子量隨物料在反應(yīng)器中停留時間的增加而增大,MWD則因?qū)挼腞TD而變寬[1-4]。
雙金屬催化劑(DMC)催化的三元環(huán)醚的開環(huán)聚合具有活性陰離子聚合的特征[5]。因聚合速率快、聚合熱大,反應(yīng)的熱負(fù)荷和安全風(fēng)險高,工業(yè)上不得不采用單體半連續(xù)滴加的“饑餓聚合”法,效率低下。最近,本課題組[6]采用微通道(MC)反應(yīng)器進(jìn)行了DMC催化的環(huán)醚開環(huán)聚合反應(yīng),大大提高了反應(yīng)的效率和安全性,但尚需通過反應(yīng)物料在反應(yīng)器內(nèi)的RTD,考察聚合產(chǎn)物MWD的變化規(guī)律。
前人對MC中的RTD已多有研究[2,7-16]。Rojahn等[2]和Rossi等[10]比較了直型、螺旋型以及螺旋轉(zhuǎn)向型MC的RTD,指出螺旋轉(zhuǎn)向型MC的RTD最窄,螺旋型MC次之,直型MC最寬。Rojahn等[2]發(fā)現(xiàn),螺旋型和直型MC中都存在臨界Reynolds數(shù)(Rec)。在Rec以下,RTD隨Reynolds數(shù)(Re)的增加而變寬,逾之則變窄,他們將其歸因于徑向二次流動[2,10,17-22]與分子擴(kuò)散之間的競爭。Re非常低時,二次流動幾乎不發(fā)揮作用,徑向混合僅依賴于分子擴(kuò)散。此時,增大Re(或流速)會減少徑向混合的時間,因而徑向混合變差、RTD變寬。但當(dāng)Re足夠高時,二次流動占主導(dǎo),分子擴(kuò)散的影響可忽略,繼續(xù)增大Re可加強(qiáng)二次流動,促使徑向混合變好、RTD變窄。螺旋轉(zhuǎn)向型MC中的RTD隨Re的增大一直變窄,沒有Rec,這是因?yàn)槁菪D(zhuǎn)向型的離心作用較強(qiáng),在Re極小時就能引起二次流動。而Rossi等[10]的研究發(fā)現(xiàn),直型、螺旋型和螺旋轉(zhuǎn)向型MC的RTD均隨Re的增大而變寬,即不存在Rec。
最近,F(xiàn)azli-Abukheyli等[4]針對MC的RTD,提出了一個新模型(PTIS模型),將徑向混合程度以及對流與軸向分散比作為模型參數(shù),為定量研究MC中宏觀RTD與微觀混合特性間的關(guān)系打下了基礎(chǔ)。本文采用低分子量的聚丙二醇(PPG)本體為介質(zhì),對不同流速和不同尺寸的MC進(jìn)行了RTD的測定,并借助PTIS模型考察了MC內(nèi)物料的混合特性。
1 實(shí)驗(yàn)部分
1.1 原料及試劑
數(shù)均分子量分別為1000、2000和4000的PPG,購自浙江紹興恒豐聚氨酯有限公司,經(jīng)4A分子篩浸泡除水、G4濾芯過濾后使用。使用前,先對各流體樣品進(jìn)行黏度測定,發(fā)現(xiàn)剪切應(yīng)力與剪切應(yīng)變率均呈良好的線性關(guān)系;110℃下三種流體樣品的黏度分別為8.5、21.7和50.3 mPa·s,屬牛頓流體。
乙醇、N,N-二甲基乙酰胺,均為分析純,購自國藥集團(tuán)化學(xué)試劑有限公司;示蹤劑酸性橙購自東京化學(xué)工業(yè)發(fā)展有限公司(上海)。
1.2 儀器及設(shè)備
紫外-可見分光光度計(jì),TU-1901型,北京普析通用儀器有限責(zé)任公司。
同軸圓筒旋轉(zhuǎn)流變儀,HAAKE RS 6000型,德國Haake公司。
螺旋型MC系由316 L不銹鋼空心管緊密纏繞在直徑為140 mm的圓柱上制得;空心管內(nèi)徑0.5或1 mm,長度6、12或30 m。MC與平流泵及進(jìn)樣器的連接示意見圖1;平流泵,2PB1040-Ⅰ型,流量范圍0.01~10 ml/min,北京星達(dá)科技有限公司;進(jìn)樣器,7725i型,上海匯興儀器儀表有限公司。
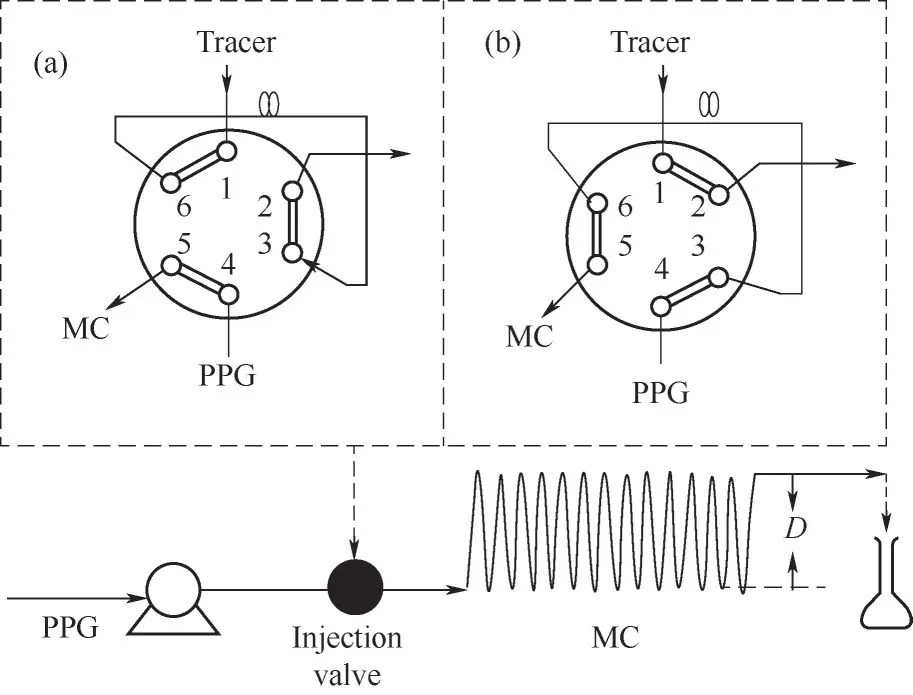
圖1 RTD測量的設(shè)備示意圖Fig.1 Equipment diagramfor RTDmeasurement
1.3 RTD的測量
按文獻(xiàn)中已報(bào)道的方式[8-10,12,15],示蹤劑通過圖1中的進(jìn)樣閥以脈沖形式注入MC中。具體原理及流程如下:(1)使進(jìn)樣閥處于狀態(tài)(a),將注射器中的示蹤劑通過位置1注入50μl定量管中,多余的示蹤劑將從位置2流出;(2)啟動PPG泵,使PPG以0.2~8.0 ml/min的流速通過位置4、5進(jìn)入MC;(3)穩(wěn)定一段時間后,旋轉(zhuǎn)進(jìn)樣閥至狀態(tài)(b)并啟動秒表,將定量管中的示蹤劑沖入MC中;(4)收集不同時間點(diǎn)MC出口處的樣品約4~8滴至容量瓶中,稱重后用乙醇稀釋至5 ml,并用紫外-可見分光光度計(jì)測定稀釋液中的示蹤劑濃度。實(shí)驗(yàn)的平均停留時間為14~2837 s;取樣時間間隔根據(jù)平均停留時間,1~20 s不等。所加示蹤劑的濃度范圍為0.02~0.1 mg/ml,標(biāo)準(zhǔn)工作曲線斜率為0.0467 ml/μg。
正式實(shí)驗(yàn)測試前,對T=110℃、μ=8.5 mPa·s、D=140 mm、u=0.021 m/s、L=6和30 m條件下的RTD做了重復(fù)實(shí)驗(yàn)測試,發(fā)現(xiàn)誤差甚小。因此,測定其余條件下的RTD時,未再做重復(fù)實(shí)驗(yàn)。
MC出口處示蹤劑濃度的計(jì)算方式如下:

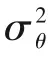
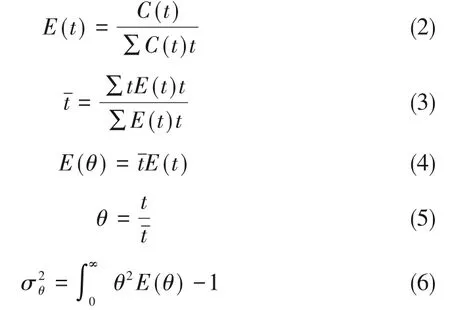
RTD模型與實(shí)驗(yàn)結(jié)果的匹配程度由式(7)所定義的相對殘差(RSSE)來表示。
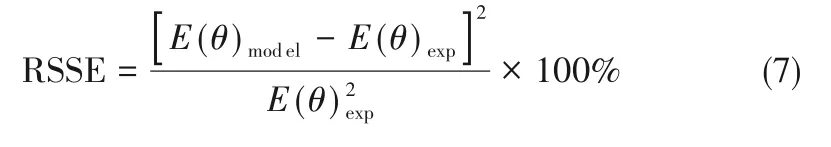
2 RTD模型
RTD的模型種類繁多,傳統(tǒng)反應(yīng)器多用經(jīng)典的多釜串聯(lián)(tanks-in-series,TIS)模型[23]。被用于MC的RTD模型則有軸向分散(axial dispersion,AD)模型[8,11]、對流模型[11]和半經(jīng)驗(yàn)?zāi)P蚚8-9,12,15,24]等。
最近,F(xiàn)azli-Abukheyli等[4]針對MC的RTD,提出了一個平行多釜串聯(lián)模型(PTIS)。它將MC內(nèi)的流體從管中心至管壁分為F層,其中,第j(1≤j≤F)層到管中心的距離為rj,第j層的厚度為Δrj。假定每一層流體的RTD均符合傳統(tǒng)的TIS模型,則總RTD為各層RTD之和,E(θ)如式(8)所示。

式中,αj、βj和Nj分別為第j子層的體積流量分率、體積分率和串聯(lián)釜的個數(shù)。它們與第j子層的體積流率Qj、體積Vj和無量綱流速vj,物料的總體積流率Q,MC的總體積V,以及無量綱徑向距離r、厚度Δr、流速v和平均流速vˉ的關(guān)系分別為:
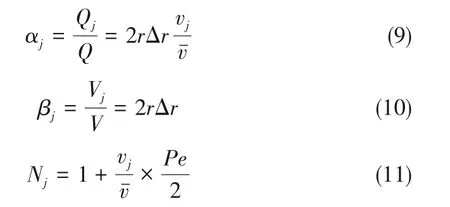
式中,Pe為對流與軸向分散的比率,即

式中,u為流速,m/s;L為管長,m;Dax為軸向分散系數(shù),m2/s。
模型中,r為徑向距離與管半徑之比,取0代表管中心,取1代表管壁;Δr為子層厚度與管半徑之比;v、vj和vˉ分別為流速、第j子層流速和平均流速與管中心處最大流速之比。
顯然,當(dāng)子層的層數(shù)F趨于無窮(即Δrj趨于0)時,RTD更逼近于實(shí)測值。模型分別用y和m來表示速度沿徑向的分布,它們與v、vˉ、r及Δr的關(guān)系見表1。若取F等于105,并將表1及式(9)~式(11)算得的vj、vˉ、αj和βj代入式(8),即得式(13)和式(14)所示的PTIS-y和PTIS-m兩種模型的RTD密度函數(shù)的表達(dá)式。

表1 v、vˉ、r以及Δr與y(或m)的關(guān)系Table 1 Relationship between v,vˉ,r,Δr and y(or m)
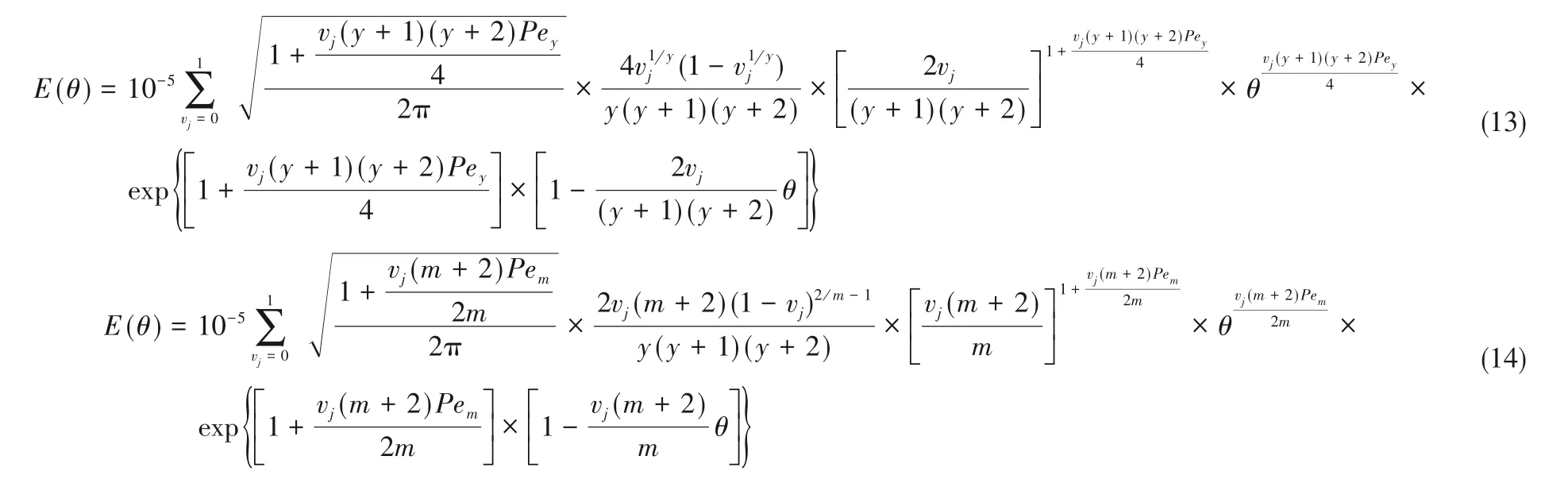
式中,模型參數(shù)Pey和Pem的物理意義均為對流與軸向分散的比率;y,m為徑向速度分布指數(shù),取值范圍分別為0~1以及1到無窮。y=0或m→∞表明不存在速度梯度,RTD最窄;y=1或m=1表明徑向速度梯度最大,RTD最寬。
諸RTD模型中,對流模型沒有可供討論的模型參數(shù),半經(jīng)驗(yàn)?zāi)P偷膮?shù)沒有實(shí)際物理意義;而徑向速度分布指數(shù)y或m一定程度上反映了徑向微觀混合程度。y越小或m越大表示徑向微觀混合越好。因而,PTIS模型一定程度上亦可用于考察MC的微觀混合特性。
3 結(jié)果與討論
3.1 PTIS模型正確性的驗(yàn)證
實(shí)驗(yàn)測定了不同尺寸的螺旋型MC中不同黏度物料的RTD,并分別用兩種形式的PTIS模型[式(13)和式(14)]關(guān)聯(lián)。作為對比,也同時采用TIS模型和AD模型[8,11,23]進(jìn)行關(guān)聯(lián),結(jié)果見圖2。可見,RTD的形狀均有輕微的拖尾,這是因?yàn)镸C中的流動可能會表現(xiàn)出圖3(b)中所示的層流特征[8-10,25-28],而非圖3(a)所示的活塞流。此外,當(dāng)MC的尺寸和物料的流速與黏度有所變化時,RTD的位置和對稱性也發(fā)生了變化,但PTIS-y模型總是與實(shí)驗(yàn)結(jié)果最為相符。
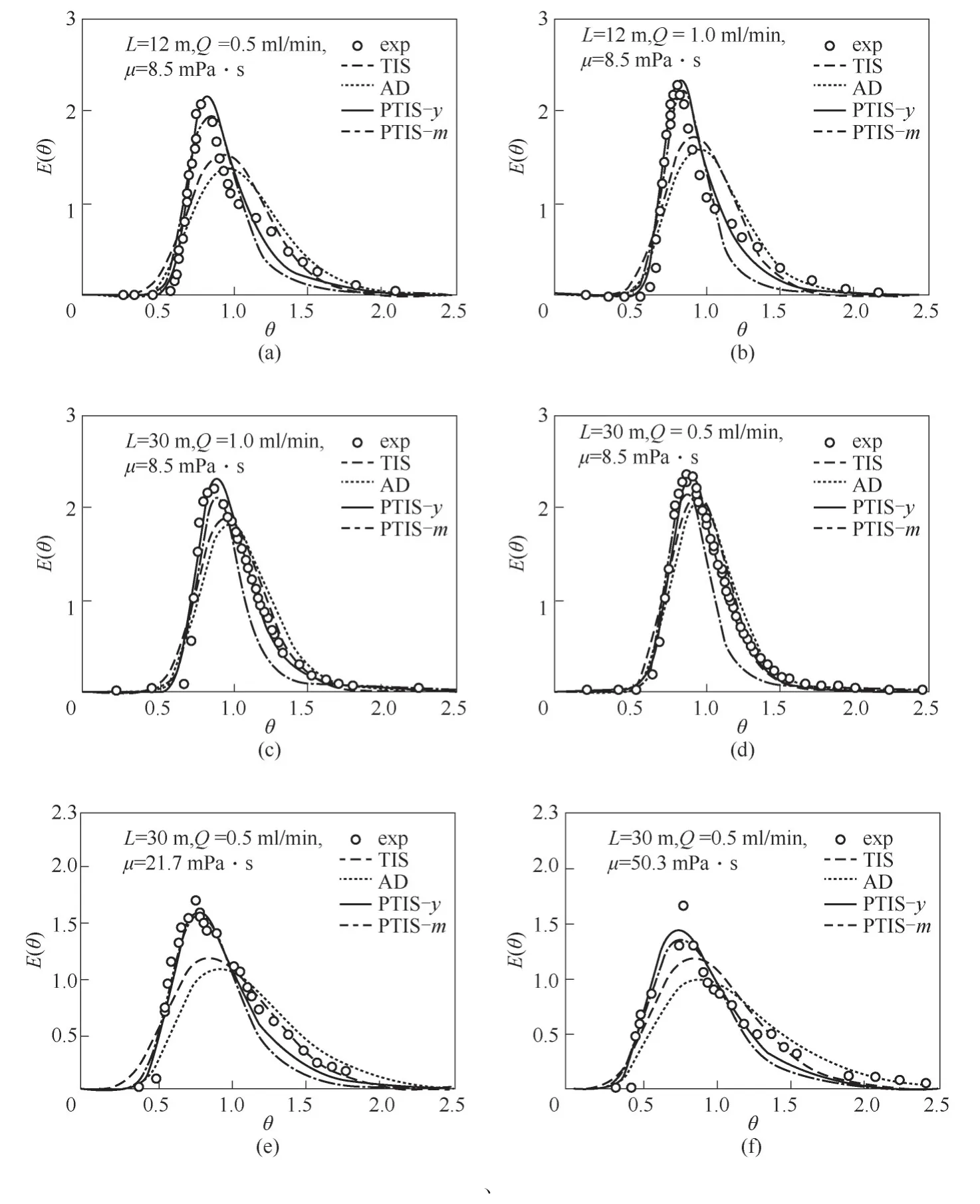
圖2 RTD實(shí)驗(yàn)結(jié)果及模型回歸圖(T=110℃,d=1 mm,D=140 mm)Fig.2 RTDexperimental data and regression results of models

圖3 活塞流與層流示意圖Fig.3 Schematic diagramof plug flow and laminar flow
進(jìn)一步從表2所列的相對殘差(RSSE)結(jié)果可見,PTIS-y模型在各種條件下都更為貼切地描述了實(shí)測的RTD。因此,本文以RTD的實(shí)測和其PTIS-y模型化結(jié)果為基礎(chǔ),進(jìn)行MC混合特性的討論。
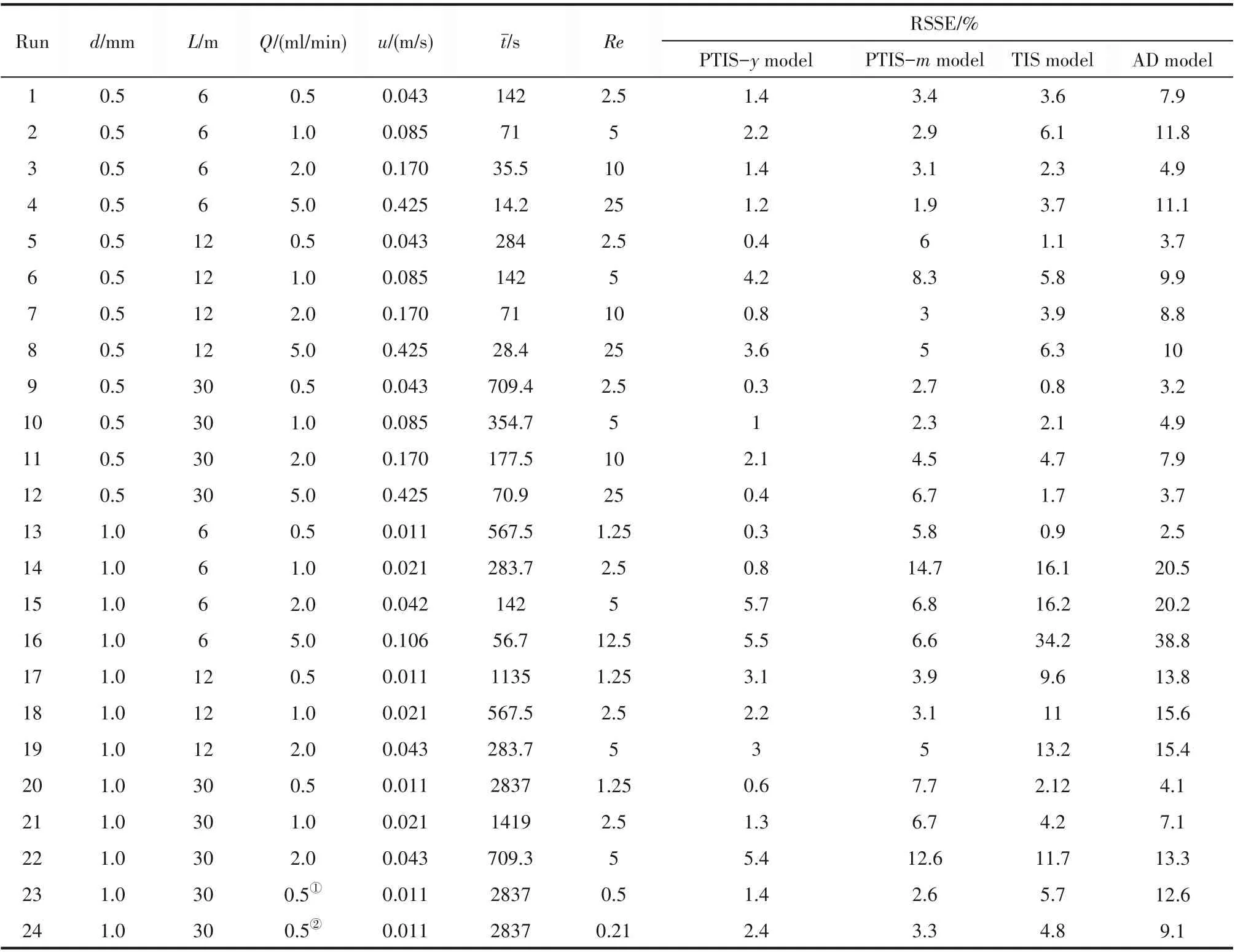
表2 RTD的模型回歸結(jié)果Table 2 Comparison of regression results with various RTD models
3.2 管長對RTD的影響
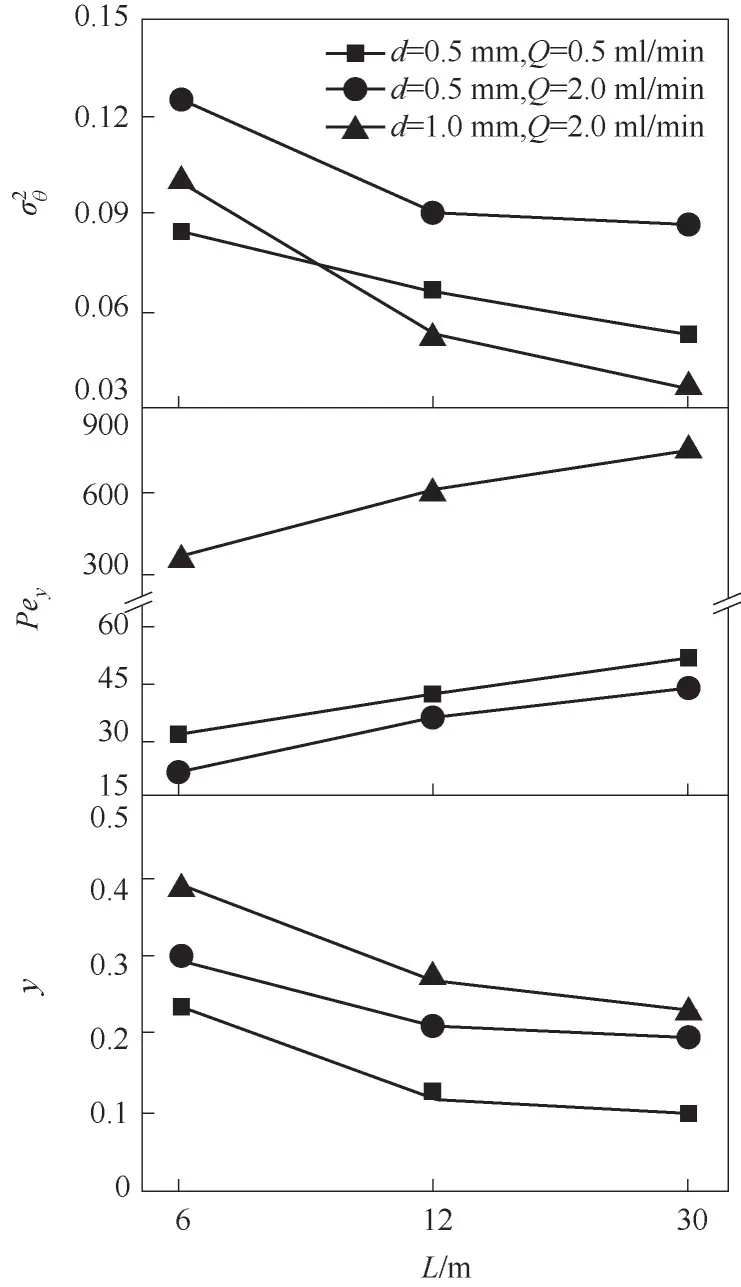
圖4 RTD方差及PTIS-y模型參數(shù)隨MC管長變化曲線(T=110℃,μ=8.5 mPa·s,D=140 mm)Fig.4 Variance of RTDand parameters of PTIS-y model vs MC of different length
3.3 Re對RTD的影響
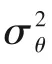

圖5 流體黏度變化時RTD方差及PTIS-y模型參數(shù)隨Re變化曲線(T=110℃,d=1 mm,L=30 m,u=0.011 m/s,D=140 mm,μ=8.5~50.3 mPa·s)Fig.5 Variance of RTDand parameters of PTIS-y model with Re when changing viscosity
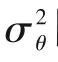
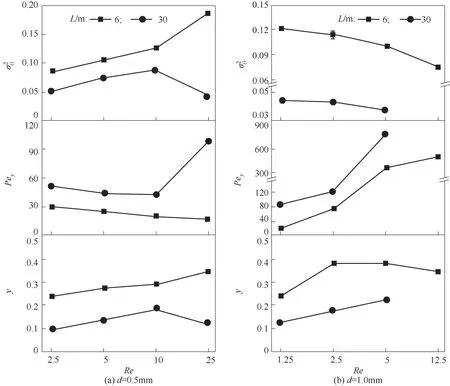
圖6 流速改變時MC中的RTD方差及PTIS-y模型參數(shù)隨Re變化曲線(T=110℃,μ=8.5 mPa·s,D=140 mm,u=0.011~0.425 m/s)Fig.6 Variance of RTDand parameters of PTIS-y model with Re when changing flow rate
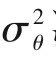
3.4 PTIS-y模型參數(shù)Pey與RTD方差的關(guān)系
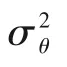

圖7 模型參數(shù)Pey與RTD方差的關(guān)系(T=110℃,d=1 mm,D=140 mm)Fig.7 Relationship between Pey and variance of RTD
4 結(jié) 論
(1)在螺旋型MC中,物料的RTD有輕微拖尾但基本對稱。與其他RTD模型相比,PTIS-y模型因徑向速度分布指數(shù)y的引入,能更好地描述MC的RTD實(shí)測值。
(2)在管徑、流速和黏度保持不變時,管長越長,對流與軸向分散的比率(即Pey)越大,反映徑向微觀混合程度的y越小,RTD越窄。表明停留時間的延長增加了徑向混合時間,使得徑向混合更為充分,減弱了軸向分散。
(3)當(dāng)保持管徑、管長和流速不變,通過降低黏度來增大Re時,黏度越低,Re越大,Pey值越大,反映徑向微觀混合程度的y越小,RTD越窄。較低的黏度可有效促進(jìn)徑向分子擴(kuò)散和二次流動,從而減弱軸向分散,使RTD變窄。
(4)在保持管徑、管長和黏度不變,通過改變流速來改變Re時,小管徑MC的徑向擴(kuò)散距離較短,徑向混合會對軸向分散造成影響,有可能出現(xiàn)一個臨界Reynolds數(shù)(Rec)。Re低于Rec時,RTD隨Re的增加而變寬;高于Rec時,RTD隨Re的增加而變窄。大管徑MC的徑向擴(kuò)散距離較長,徑向混合不足以影響到軸向分散,RTD會隨著Re的增大而變窄。
(5)改變MC管長、物料黏度或流速中的一個,模型參數(shù)Pey與RTD的方差始終呈相反的變化趨勢,即Pey越大,RTD越窄。這說明在單因素改變的前提下,PTIS-y的模型參數(shù)Pey可直接代表RTD的寬窄。
致謝:本文研究過程中,得到中國科學(xué)院大連化學(xué)物理研究所陳光文老師、清華大學(xué)駱廣生老師和王凱老師在實(shí)驗(yàn)儀器、設(shè)備及方法等方面的指導(dǎo)和幫助,在此謹(jǐn)表感謝!
符號說明
D——螺旋線圈的直徑,mm
d——微通道的內(nèi)徑,mm
m——PTIS-m模型中速度分布指數(shù)
Pe,Pey,Pem——分別為Peclet數(shù)、PTIS-y模型中的Peclet和PTIS-m模型中的Peclet數(shù)
T——溫度,℃
y——PTIS-y模型中速度分布指數(shù)
μ——PPG的黏度,mPa·s

