基于DP的隨機模型預測控制能量管理研究

馬永娟 尹燕莉 馬什鵬

（重慶交通大學機電與車輛工程學院）

近年來，有越來越多的學者應用模型預測控制（Model Predictive Control,MPC）來解決混合動力汽車能量管理優化問題[1-11]。它的主要原理是可以通過提前預測獲取未來有限時間內的車輛運行信息，然后實施轉矩的優化分配。可采用指數預測[12]、馬爾科夫鏈[13]等方法預測未來時間內的車輛運行狀態，然后優化算法[14-17]對預測信息進行求解。本文以超輕度混合動力汽車為研究對象，提出基于動態規劃（DP）求解的隨機模型預測控制能量管理策略。

1 超輕度混合動力汽車模型

1.1 系統結構與參數

本文對一款具有并聯結構的超輕度混合動力汽車展開研究。其主要部件除了發動機、電動機及電池外，增加了一個回流式無級自動變速傳動系統實現動力源之間的傳遞。該車具有純發動機驅動、純電機驅動、行車充電及制動能量回收4個工作模式。結構簡圖如圖1所示。

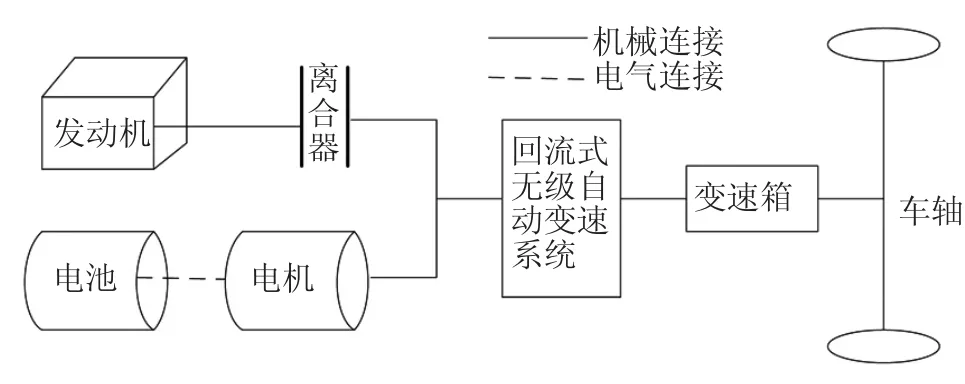
圖1 超輕度混合動力汽車結構簡圖

1.2 車輛動力學模型

汽車在行駛的過程中，需要克服滾動阻力、空氣阻力以及加速阻力（本文不考慮坡度阻力）。車輛在任意工況下的整車縱向動力學模型如式（1）：

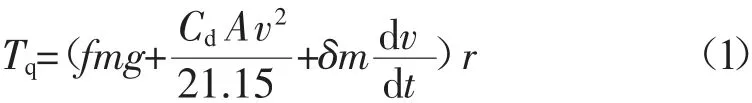
式中：Tq——車輛需求轉矩，N·m；

m——整車質量，kg;

g——重力加速度，m/s2；

f、Cd、δ——車輛的輪胎滾動阻力系數、空氣阻力

系數、旋轉質量換算系數；

A——迎風面積，m2；

d v/d t——車輛加速度，m/s2；

r——車輪半徑，m。

2 基于DP的隨機模型預測控制能量管理策略研究

2.1 基本理論介紹

2.1.1 模型預測控制原理

模型預測控制(MPC)是一種先進的控制方法，在工業控制中得到廣泛應用。它主要以不同預測模型為基礎，預測系統未來輸出，采用滾動優化原則，在有限時域內反復在線優化得到最優的控制量。模型預測控制的框架結構如圖2所示，可以分為3個部分：預測模型、滾動優化及反饋校正。其基本思想可以概括為：在每一個采樣時刻，利用預測模型結合當前測量信息，采用優化算法在線滾動求解一個有限時域的優化問題，并將所得優化解的第1個元素作用于被控系統，將實際輸出值反饋給預測模型修正預測值，并刷新優化問題重新求解[18]。，然后在下一采樣時刻重復此過程直到有限時域結束。

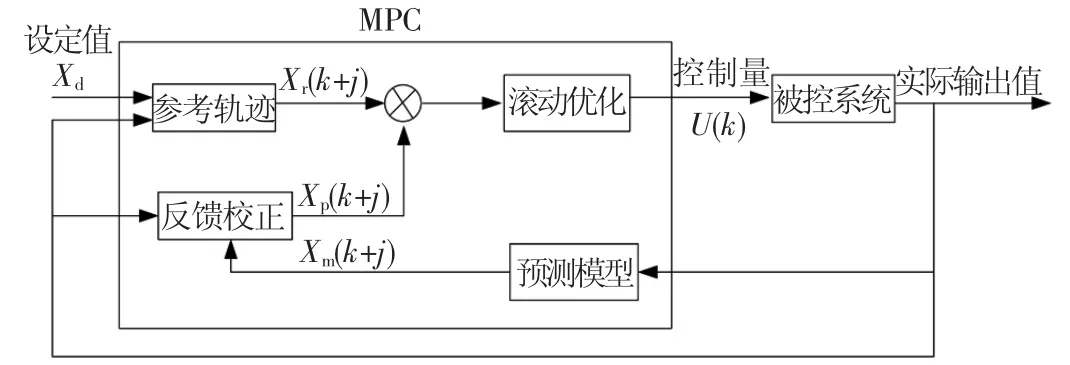
圖2 模型預測控制總體框架圖

2.1.2 動態規劃原理

動態規劃作為一種全局優化算法，本質是求解多階段的決策問題。假設將待求解的問題看作是一個整體，把整體劃分為有限個相互關聯又具有獨立性的個體，通過直接求解各個個體之間的決策問題，會得到多個決策序列，能夠使整體的效果達到最優的決策序列就是動態規劃算法所求出的問題的解。

動態規劃的求解過程可概括為：逆向計算、正向尋優。逆向計算就是通過將待求問題分解為n個階段，從最后1個階段n開始，依次向前直至第1個階段，迭代計算每個階段每一狀態下的最優目標函數值，從而得到與之相對應的最優控制變量。正向尋優就是基于逆向計算的結果，給定1個初始值，通過狀態轉移方程插值得到第1階段至最后1個階段的最優控制變量序列。動態規劃原理如圖3所示。

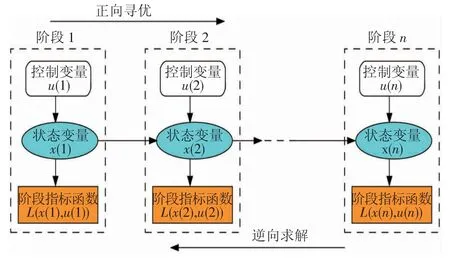
圖3 動態規劃原理圖

2.2 基于DP的隨機模型預測控制能量管理策略

利用模型預測控制對混合動力汽車進行能量管理，就是對未來一段時間內的電機轉矩和發動機轉矩進行最優分配。首先基于馬爾可夫模型預測出有限時域內的加速度信息，然后采用DP算法進行優化求解，獲得轉矩分配序列。利用反饋機制實現閉環控制，獲得最優的分配結果。

2.2.1 基于馬爾可夫模型的加速度預測

預測模型相當于整個MPC能量管理策略框架中的“基石”，通過預測模型提前獲知混合動力汽車未來一段時間內的運行狀態，如車速、加速度及需求功率等信息，便可以根據當前時刻車輛的運行狀態在預測時域內運用優化算法控制車輛性能達到該時域內的最優狀態，從而獲得更高的燃油經濟性。

在車輛運行時，加速度的變化具有隨機性，能夠準確描述汽車的實際行駛過程，且未來某一時刻的加速度只取決于當前時刻的加速度，與歷史加速度信息無關，具有馬爾可夫性質，因此，可建立馬爾可夫加速度預測模型對加速度進行預測。

構建馬爾可夫加速度預測模型的關鍵是計算加速度的轉移概率矩陣，轉移概率矩陣的每一個元素代表汽車加速度從當前狀態轉移到下一狀態的概率，如式（2）。選取概率最大的值作為加速度的實際值，從而確定下一時刻的加速度變化。

式中：a(k)、a(k+1)——當前時刻和下一時刻的加速度；

Pi,j——加速度由當前狀態i轉移到下一狀態j的概率。

可根據式（3）來計算轉移概率矩陣。

式中：Si——加速度由當前狀態i轉移的總次數；

Si,j——在預測時域p內，加速度由當前時刻狀態i轉移到下一狀態j的次數。

選取ECE_EUDC、UDDS2種工況來提取加速度信息。將加速度（-1.5～1.5 m/s2）按一定間隔離散，采樣步長取1 s，預測時域為p。根據以上所建立的馬爾可夫加速度預測模型，對加速度進行預測。

圖4表示車速為40 km/h時加速度的轉移概率。由圖中可以看出，加速度的轉移概率基本呈對角線分布，分布較集中。這是因為在1 s的時間范圍內，實際駕駛時通常不會改變行駛狀態，所以加速度涵蓋的變化信息較少，相差不大，使得下一時刻加速度與當前時刻加速度分布在相近區間。

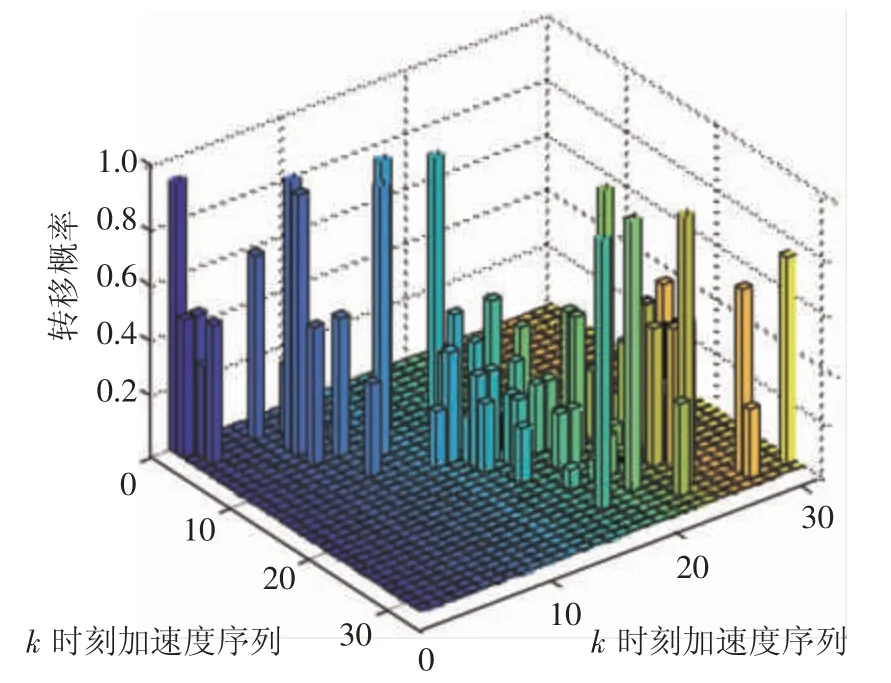
圖4 v=35 km/h時加速度的轉移概率

2.2.2 基于DP求解的滾動優化過程

根據馬爾可夫模型預測獲得的加速度信息，通過式（1）求解獲得預測時域內的需求轉矩。將燃油消耗作為優化目標，選取電機轉矩Tm為控制變量，電池SOC為狀態變量，采用DP求解有限時域內最優的轉矩分配。

1）目標函數和約束條件

通過等效因子將電池能量變化等效為燃油消耗，構建以整車等效燃油消耗量最小以為目標的回報函數，如式（4）所示：

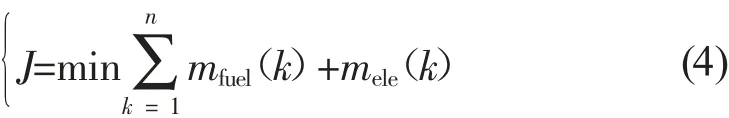
式中：mfuel（k）——當前k時刻發動機燃油消耗量，g；

mele（k）——當前k時刻電池等效燃油能量，g。

在優化過程中，每一階段的決策之后，會引起狀態的轉移，狀態轉移方程如式（5）：

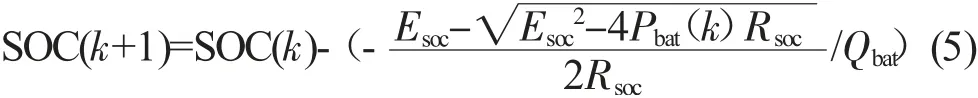
式中：SOC(k)、SOC(k+1)——表示當前k時刻和下一時刻的荷電狀態；

Esoc——當前狀態下的電動勢；

Rsoc——表示當前狀態下的內阻；

Qbat——電池容量；

Pbat（k）——當前k時刻的電池功率。

同時，為防止轉矩、轉速等因素對優化結果造成干擾，因此，在預測時域k～k+p對相關變量做如下約束：

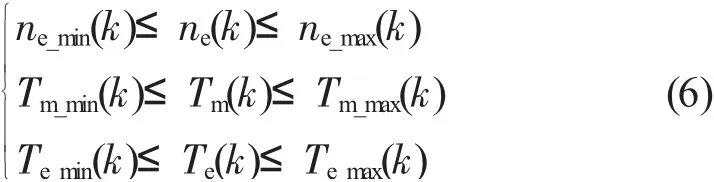
式中：ne(k)——k時刻的發動機轉速，r/min；

ne_max(k)、ne_min(k)為k時刻發動機轉速的最大、最小值，r/min；

Tm(k)——k時刻的電動機轉矩，N·m；

Tm_max(k)、Tm_min(k)——k時刻電機轉矩的最大、最小值，N·m；

Te(k)——k時刻的發動機轉矩，N·m；

Te_max(k)、Te_min(k)——k時刻發動機的最大、最小值，N·m。

2）DP優化求解過程

動態規劃（DP）作為一種全局最優算法，在模型預測控制當中，對預測時域內的預測信息進行滾動優化求解，可提高計算效率，具體優化步驟如下：

（1）根據馬爾可夫模型預測獲取的加速度信息，結合式（1）求出預測時域內的需求轉矩[Tm(k)~Tm(k+p)]；

（2）在預測時域k～k+p內，可將優化問題劃分成p+1個子階段[k，k+1，…，k+p]，并將狀態變量SOC在約束范圍內進行離散化處理；

（3）根據上文的目標函數和約束條件，首先從最后一個階段k+p逆行求解，求出該階段到上一階段k+p-1的最小油耗值，并記錄獲得最低油耗時的控制變量Tm，依次逆向計算直到第k階段，則整個逆向求解過程結束；

（4）從初始階段開始正向尋優，根據k階段的狀態變量SOC(k)，插值找到SOC(k)所對應的最小燃油消耗量fuel(k)和電動機轉矩Tm(k)，根據狀態轉移方程（式5）獲得下一時刻的狀態量SOC(k+1)，重復（3），直到k+p時結束，就能獲得k～k+p內的最優電機轉矩分配序列[Tm(k)，Tm(k+1/k)，…，Tm(k+p/k)]。

2.2.3 實施反饋校正

通過DP求解獲得最優電機轉矩分配序列之后，只將最優序列的第1個控制量Tm(k)施加給車輛。在下一個時刻，首先檢測車輛的實際車速和加速度值，并將其反饋給預測模型，重新預測系統輸出并實施優化求解，重復執行上述過程直到預測時域結束，即可獲得預測時域內的最優轉矩分配。整個控制過程的流程圖如圖5所示。

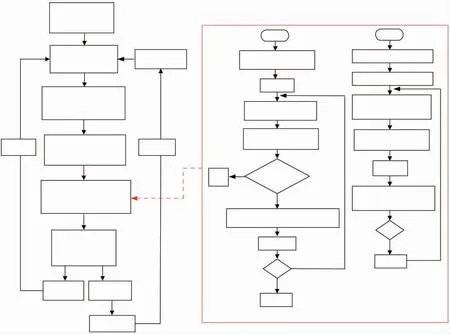
圖5 基于DP的隨機模型預測控制流程圖

3 仿真結果分析

為驗證所提控制策略的性能，利用Matlab/Simulink仿真平臺，基于ECE_EUDC、UDDS標準循環工況進行整車仿真分析。選取預測時域為3 s，采樣時間間隔為1 s；將電池SOC限定0.3~0.8之間，以0.1為間隔進行離散，SOC初始值設為0.6；將預測時域內的需求轉矩以5 N·m的間隔進行離散。仿真結果如圖6所示。圖6a為仿真工況數據圖，圖6b為發動機轉矩隨仿真工況的車速變化軌跡，可以看出，在汽車加速情況下，所需要的車輪處轉矩較大，發動機多呈工作狀態，輸出較大轉矩。圖6c、6d為電機轉矩及電池SOC變化軌跡，可看出，當電動機轉矩為正時，電機作為電動機，使用電能，使電池SOC下降；當電動機轉矩為負時，電機作為發電機，進行發電，使電池SOC上升。綜合觀察圖6，當車速較低、頻繁啟動時多用電動機驅動，當車輛速度較高時，多用發動機，同時給電池充電。這與我們平時熟知的混合動力汽車理想轉矩分配結果相同，說明所提出的控制策略具有一定的可行性。

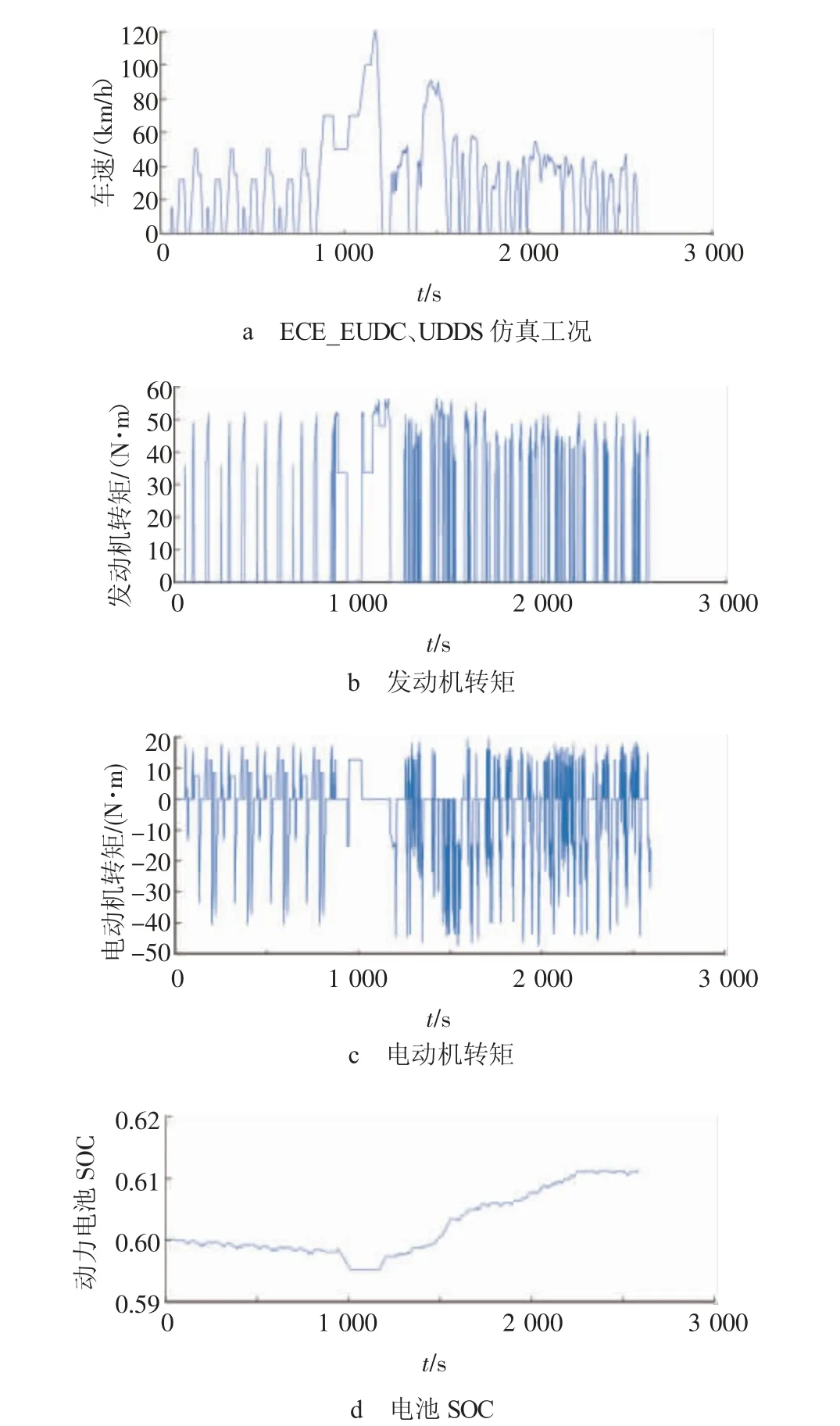
圖6 仿真結果圖

4 結論

本文將MPC控制理論與DP算法有效結合，實現了超輕度混合動力汽車良好的轉矩分配控制。基于ECE_EUDC、UDDS標準循環工況為樣本數據構建馬爾科夫模型對加速度進行預測，對預測時域內的信息采用DP算法進行滾動優化求解，然后實施反饋控制獲得最優轉矩分配。將所提控制策略基于Matlab/Simulink平臺進行仿真分析，仿真結果表明，發動機和電動機基本工作在最優轉矩區域內，證明該策略能取得良好的控制效果以及實現超輕度混合動力汽車最優的能量管理。