弱非線性內(nèi)孤立波在斜坡上的傳播演化特性

郅長紅,陳 科，尤云祥

(上海交通大學 三亞崖州灣深海科技研究院，海南 三亞 572000; 上海交通大學 海洋工程國家重點實驗室，上海 200240)

海洋內(nèi)孤立波是在密度層化海洋內(nèi)部一種常見的波動，尤其發(fā)生在近海沿岸及海峽周圍.Cai等[1]在中國南海發(fā)現(xiàn)具有穩(wěn)定波峰的內(nèi)孤立波，這些內(nèi)孤立波周期長、波高大，有的甚至能達到100 m，于是當這些攜帶了巨大能量和動量的內(nèi)孤立波傳播至陸架海域時，會對近岸海洋結(jié)構(gòu)物造成巨大的動載荷，從而危害其生產(chǎn)和生存安全[2-5].在軍事領(lǐng)域，海洋內(nèi)波導致的密度面脈動能影響水下聲波的傳播，嚴重影響水下目標的探測和定位，甚至引發(fā)潛艇失控等重大事故.在民用上，內(nèi)波頻發(fā)對海上作業(yè)平臺和水下生產(chǎn)設(shè)備也會造成巨大的影響.我國南海北部海域地形復雜且密度垂向?qū)踊卣髅黠@，是內(nèi)波頻發(fā)的海域，為保障海上作業(yè)安全和規(guī)避可能的海下作業(yè)的風險，深刻理解在南海海域內(nèi)波的生成演化傳播機制具有重大的意義.

在理論與數(shù)值研究方面，弱非線性內(nèi)孤立波在平坦地形上的傳播已經(jīng)被廣泛研究.為描述內(nèi)孤立波在斜坡上的傳播過程，張善武[6]利用該理論很好地對南海北部的內(nèi)孤立波的傳播演化進行了模擬.Helfrich等[7]提出了三階非線性項的KdV(Korteweg-de Vries)方程，但他并未對KdV理論做進一步的適用性分析.為定量地衡量非線性和色散性，黃文昊等[8]又通過系列模型試驗給定了上述KdV理論的適用范圍,并基于以上理論針對張力腿平臺建立了載荷計算理論模型[9].Hsieh等[10]通過數(shù)值計算研究了不同斜坡坡度對內(nèi)孤立波傳播的影響.

過去的50年，不少國內(nèi)外學者也相繼通過實驗對內(nèi)孤立波與多種地形(如拱形底、梯形底、三角形、半球形及斜坡等)的相互作用做了不同方面的研究.研究發(fā)現(xiàn)弱非線性的KdV理論適用于大部分內(nèi)波的傳播演化.Kao等[11]在研究內(nèi)孤立波向坡度為 1∶16和1∶9的斜坡上傳播時，發(fā)現(xiàn)在淺化過程中波背面逐漸變陡，隨后破碎，他們將其歸因于界面的剪切不穩(wěn)定.Helfrich等[7]在研究下凹型的內(nèi)孤立波在斜坡上傳播演化時發(fā)現(xiàn)初始波會分裂為多個上凸型的類孤立波以及尾波鏈.杜輝等[12]等對內(nèi)孤立波在緩坡上的破碎及能量分析進行了深入的討論.屈子云等[13]等通過實驗研究發(fā)現(xiàn)了突變地形對內(nèi)孤立波形態(tài)的影響.

本文采用變系數(shù)KdV(Variable-Coefficient Korteweg-de Vries,vKdV)方程來模擬內(nèi)孤立波在緩坡上的傳播演化過程.盛立等[14]的研究結(jié)論表明平坦地形下常系數(shù)的KdV方程適用于弱非線性內(nèi)孤立波的傳播演化.故本文采用KdV的解作為初始波，并用vKdV方程數(shù)值模擬弱非線性的內(nèi)孤立波的在斜坡上的傳播演化過程.因此本文中設(shè)計了兩種坡度的斜坡，用以研究弱非線性內(nèi)孤立波在斜坡上傳播時的演化特性，討論了斜坡的坡度對弱非線性內(nèi)孤立波傳播的影響.除此之外，對弱非線性內(nèi)孤立波在經(jīng)過斜坡后的演化波進行深入的研究.通過本文工作，希望能揭示在較為復雜地形上內(nèi)孤立波的傳播規(guī)律.

1 理論模型

考慮有限深兩層流體中內(nèi)孤立波在斜坡上的傳播演化問題.假設(shè)兩層流體均是不可壓縮且無旋的理想流體.建立直角坐標系Oxz，其中Ox位于兩層流體未擾界面處，Oz垂直向上為正.設(shè)上、下層流體密度分別為ρ1、ρ2，底部最大深度處到未擾界面處的距離為常數(shù)H2.記地形高度函數(shù)為b(x)，上層流體深度為h1，則下層深度為h2=H2-b(x).

設(shè)上下兩層流體的速度勢為φi(i=1，2，分別表示上、下層流體)，壓力為pi.記內(nèi)孤立波的振幅和特征波長分別為a及λ，特征水深為h0，地形特征高度為b0.定義內(nèi)孤立波的非線性參數(shù)ε=a/h0，色散系數(shù)μ=(h0/λ)2，地形高度參數(shù)為β=b0/h0.對各物理量進行無因次變換如下：

(1)

式中：t為時間；g為重力加速度；ζ為兩層流體界面的垂向位移；帶星號的量表示無因次物理量.

首先定義上、下兩層流體中水平速度沿深度方向積分的平均速度：

(2)

(3)

Choi等[15]提出了平坦地形下的MCC (Miyata-Choi-Camassa)方程，用以描述強非線性內(nèi)孤立波.當在有地形的情況下，通過改變MCC控制方程中的底部邊界條件和界面水動力條件得到：

(4)

(5)

(6)

(7)

(8)

取地形函數(shù)b(x)=bα(αx)，其中α為地形坡度參數(shù).那么對弱非線性地形，βα=O(μ)，O表示精度.式(6)簡化為

(9)

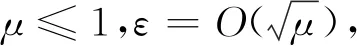
(10)

(11)

若直接采用式(10)和(11)來模擬內(nèi)孤立波在斜坡上傳播演化過程，尤其是地形較為復雜時，在進行數(shù)值時會遇到Kelvin-Helmholtz不穩(wěn)定性問題，從而增加了計算的工作量.因此，若能對其進行簡化，化為只與界面位移有關(guān)的單一方向模型，將大大提高大尺度范圍的計算效率.保留O(ε)的平方非線性項，最終式(10)和(11)可化為變系數(shù)KdV方程：

ζt+c0(x)ζx+c1(x)ζζx+c2(x)ζxxx+

(12)

(13)

KdV方程的內(nèi)孤立波解為

ζ=asech2[λKdV(x-cKdVt)]

(14)

vKdV方程在文獻[16]中也有提及.

2 結(jié)果與分析

2.1 初始條件

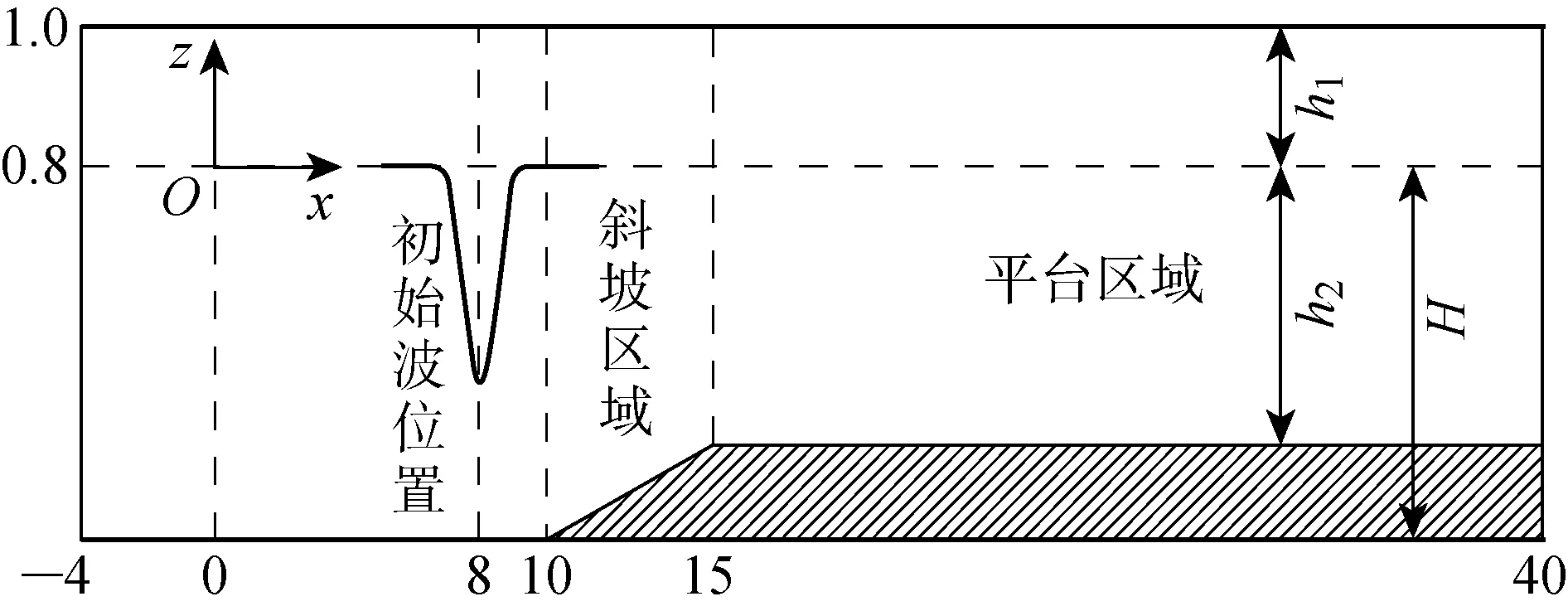
圖1 數(shù)值水槽示意圖(m)Fig.1 Schematic diagram of numerical flume (m)

對式(12)進行數(shù)值計算時，對于空間以及時間上分別采用有限差分法和四階Runge-Kutta數(shù)值離散方法.初始波為KdV方程的定態(tài)解(式(14))，其無因次振幅分別為a/h1=-0.164,-0.237，-0.310 5.本文在對vKdV方程進行數(shù)值模擬時采用與黃文昊等[8]實驗中相同的初始條件，如圖1所示，數(shù)值水槽的無因次全長L/h1=200，水深h=1.0 m，上、下層流體深度比為1∶4.內(nèi)孤立波的無因次初始位置為x0/h1=50，表1中給出了具體的內(nèi)孤立波傳播演化初始條件.網(wǎng)格尺寸大小為Δx=0.1，Δt=0.005.這里設(shè)計了兩種坡度δ=1/10和7/50的斜坡，不同坡度是通過調(diào)整斜坡區(qū)域的垂直高度而保證水平方向的長度不變得到的.文獻[8]表明：存在臨界色散系數(shù)μ0=0.1，KdV定態(tài)解適用于弱色散弱非線性(ε≤μ，μ<μ0)工況.盛立等[14]通過數(shù)值計算發(fā)現(xiàn)KdV傳播模型適用于弱色散弱非線性工況，可用來傳播KdV方程的定態(tài)解.基于此，本文采用式(12)所述方程傳播弱非線性內(nèi)孤立波是合理的.

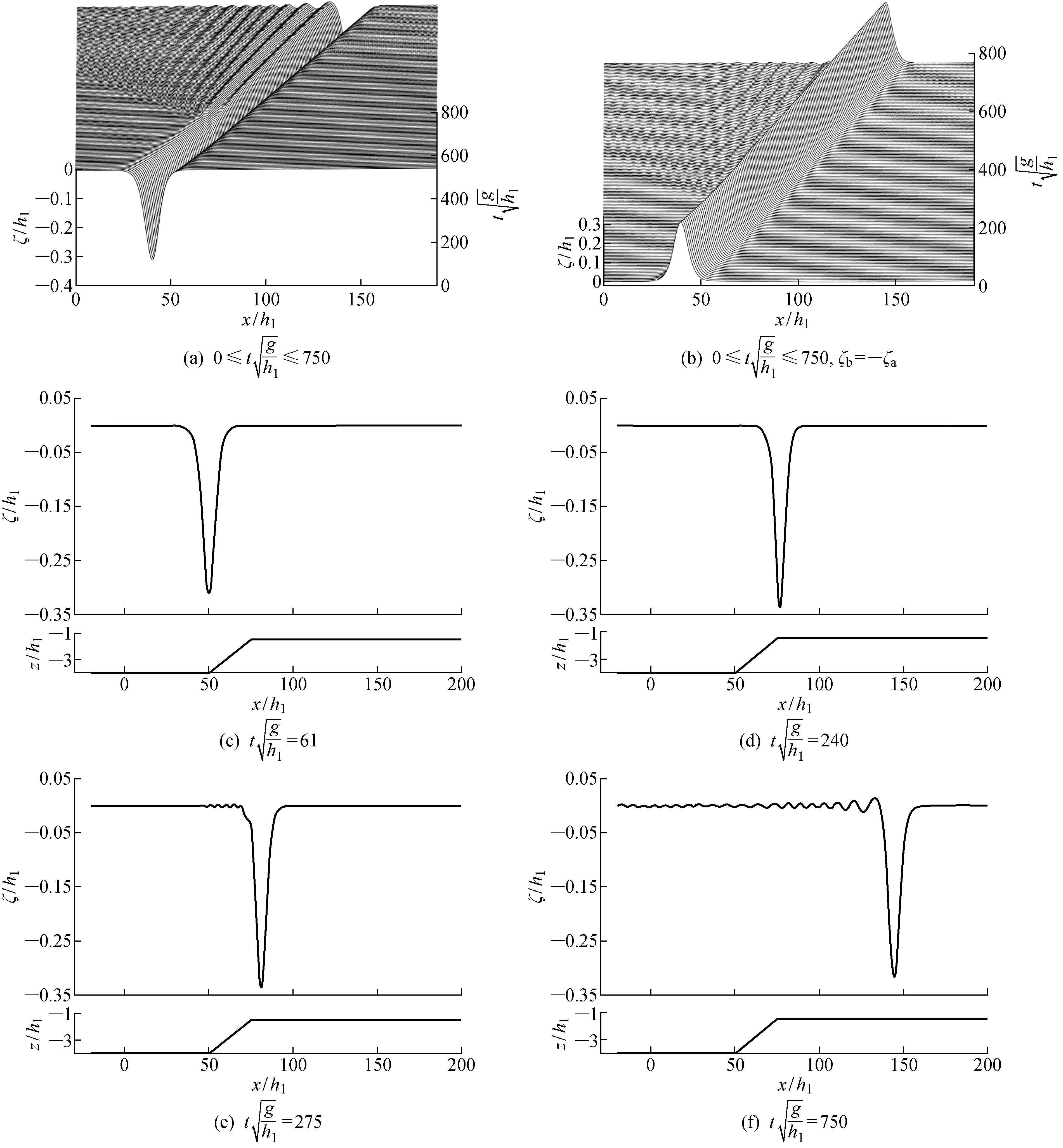
圖2 δ=1/10,h1/h2=1/4,a/h1=-0.310 5時內(nèi)孤立波在斜坡上傳播的演化特性Fig.2 Propagation evolution characteristics of internal solitary waves on slope at δ=1/10,h1/h2=1/4,and a/h1=-0.310 5

表1 內(nèi)孤立波傳播演化初始條件Tab.1 Initial conditions of propagation and evolution of internal solitary waves

2.2 弱非線性內(nèi)孤立波在斜坡上的傳播演化

內(nèi)孤立波在坡度為1/10的斜坡上的傳播過程時波形變化并不是特別明顯，當?shù)竭_斜坡頂端x/h1=50時背部產(chǎn)生了一個突起(圖2(c))，并隨著波的傳播，波背面突起逐漸增大并演化成為一系列分散開來的尾波列(圖2(d)～2(f))，首波的前后兩端也不再對稱.

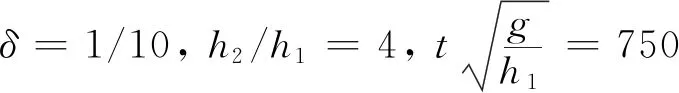
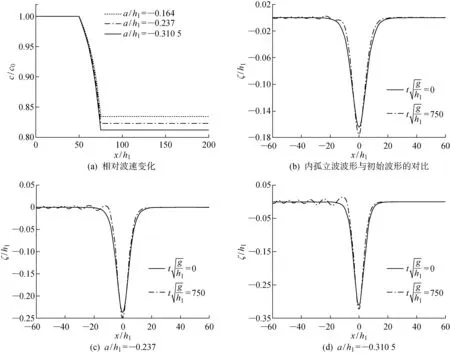
圖時不同振幅內(nèi)孤立波在斜坡上的傳播演化特性Fig.3 Propagation evolution characteristics of internal solitary waves at different amplitudes on slope at δ=1/10,h2/h1=4,and

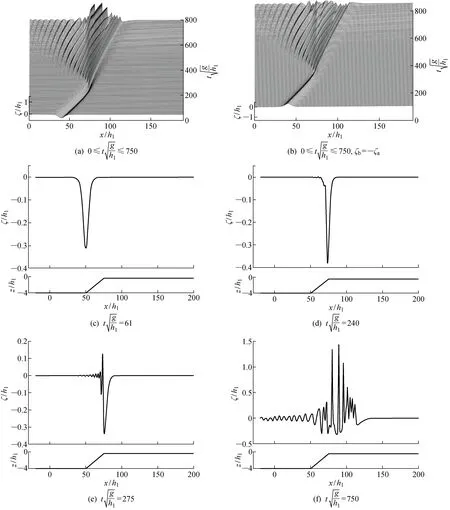
圖4 δ=7/50,h1/h2=1/4,a/h1=-0.310 5時孤立波在斜坡上傳播的演化特性Fig.4 Propagation evolution characteristics of internal solitary waves on slope at δ=7/50,h1/h2=1/4,and a/h1=-0.310 5

圖4所示為a/h1=-0.310 5 的內(nèi)孤立波在坡度為7/50斜坡上的傳播演化過程.數(shù)值結(jié)果是由vKdV (式(12))模型傳播定態(tài)弱非線性內(nèi)孤立波(式(14))計算得到.與坡度為1/10的情況相比，在上游形成的突起幅度明顯變大(圖4(c))，且在上游形成振幅較大的尾波列，首波不再對稱.由圖4(a)和4(b)能清楚地看到在較大坡度的斜坡的作用下振幅隨時間的變化關(guān)系.與δ=1/10的情況不同之處在于：當δ=7/50時，振幅先增加后減小，內(nèi)孤立波由下凹型變?yōu)樯贤剐?當δ=1/10時，振幅先增大后趨于穩(wěn)定，內(nèi)孤立波的極性并未發(fā)生改變.上述演化特性是由于在與斜坡相互作用的初期，斜坡的淺化作用起主導作用，使得振幅增加.隨著坡度進一步增大，演化過程中會導致兩層流體密度層的混合和波面背部不斷變陡，從而使得剪切作用不斷增強，由此導致首波能量的損失遠大于淺化作用，此時能量耗散作用起主導作用，因此振幅減小.如圖 4(c)～4(f)所示，首波波前變得平坦，幾乎與斜坡平行，波背部則逐漸變陡，波形最終變?yōu)樯贤剐?值得注意的是，當斜坡坡度為7/50時，上下層流體深度比h1/h2變?yōu)?，上層流體深度大于下層流體深度，說明內(nèi)孤立波在斜坡上時經(jīng)過了臨界點(h2/h1=1)，由式(6)中可以看到，c1(x)=0 (即h1=h2)處是內(nèi)孤立波極性轉(zhuǎn)變的臨界點，此時需要立方非線性項來更好地描述上下層流體深度相等時內(nèi)孤立波的極性轉(zhuǎn)變過程[7].因此算例中當上層流體大于下層流體時，內(nèi)孤立波會由下凹型轉(zhuǎn)變?yōu)樯贤剐?

弱非線性內(nèi)孤立波在通過斜坡傳播時的演化特性與波受到由下層流體深度減小而導致的淺化效應(yīng)以及在與斜坡相互作用下的能量耗散作用有關(guān).此時由于上下層流體深度的變化導致一系列尾波的產(chǎn)生，使得內(nèi)孤立波振幅減小，而淺化效應(yīng)使振幅增大.斜坡坡度越大，非線性越強，作用于內(nèi)孤立波上的能量耗散作用逐漸超過淺化作用，故而呈現(xiàn)出振幅先增加后減小的趨勢，當內(nèi)孤立波經(jīng)過臨界點后，波形由下凹型變?yōu)樯贤剐停莼蟮牟ㄈ匀荒苡肒dV理論來表征.

3 結(jié)論

在模擬弱非線性內(nèi)孤立波在斜坡上的傳播演化時，vKdV方程更為簡便高效，能適用于大部分常見的內(nèi)孤立波.采用vKdV方程對弱非線性內(nèi)孤立波建立了相應(yīng)的數(shù)值計算模型模擬并研究其在不同坡度的斜坡上的傳播演化特性，主要結(jié)論如下：

(1)當斜坡坡度較小時，弱非線性內(nèi)孤立波經(jīng)過斜坡上的傳播演化時其受到的淺化效應(yīng)大于能量耗散作用，振幅逐漸增加直至在平坦區(qū)域趨于穩(wěn)定，且隨著斜坡坡度的增加，該現(xiàn)象愈加明顯.內(nèi)孤立波在斜坡上傳播時會形成尾波列，尾波的振幅會隨著斜坡坡度的增加而增大.

(2)在相同的地形條件下，非線性越強的內(nèi)孤立波受到的來自斜坡的作用力越大，阻礙作用越明顯，表現(xiàn)為振幅越大的內(nèi)孤立波在傳播過程中振幅的增加量越小，波速的減小量越大.隨著斜坡坡度的增大，弱非線性內(nèi)孤立波在傳播過程中受地形因素導致的能量耗散作用逐漸超越淺化作用，因此內(nèi)孤立波在傳播過程中表現(xiàn)出振幅先增加后減小的特性.當在斜坡傳播經(jīng)過臨界點后內(nèi)孤立波由下凹形轉(zhuǎn)變?yōu)樯贤剐停以谏嫌萎a(chǎn)生了一系列振幅逐漸衰減的尾波列.