非均勻流場螺旋槳空泡數值模擬
劉 恒,伍 銳,3,孫 碩
(1.上海船舶運輸科學研究所 航運技術與安全國家重點實驗室,上海 200135;2.上海船舶運輸科學研究所 航運技術交通行業重點實驗室,上海 200135;3.浙江大學 能源工程學院化工機械研究所,杭州 310027)
19世紀末,英國學者就開始注意到螺旋槳空化現象,空泡的發生導致螺旋槳工作于水汽中,螺旋槳推力下降,航速難以達到預期[1].空化其實是一種熱力學現象,環境壓力不變當溫度升高時,液體吸收熱量發生汽化;溫度下降時,水汽冷凝成液體狀態.對于螺旋槳空化而言,溫度一定,槳葉高速旋轉,槳葉表面壓力低至飽和蒸汽壓力時,液體水分子汽化,水汽通過界面進入氣核使之膨脹發展為肉眼可見空泡;當槳葉表面壓力升高,空泡發生潰滅,釋放熱量,產生劇烈壓力脈沖.常見的螺旋槳空泡形態有片空泡、梢渦空泡、泡空泡、葉根空泡、云霧狀空泡及轂渦空泡等,其中梢渦空化起始最早,會導致螺旋槳輻射噪聲驟增,水下航行器臨界航速的高低完全取決于此.因此,如何延緩梢渦空泡的產生對于槳的設計者而言至關重要,而準確預測梢渦空化則是低噪聲螺旋槳設計的前提和基礎.
相對于試驗而言,數值模擬能夠以較低的成本、更高的效率及能提供更加豐富的流場信息而成為研究螺旋槳空化流動的重要手段.空化數值模型大體分為三類:界面追蹤法[2]、全流場求解Navier-Stokes(N-S)方程均相流模型[3]及歐拉-拉格朗日混合方法[4].其中N-S方程全流場求解應用最為廣泛,該方法將液相和氣相均視為連續流體介質.朱志峰等[5]以E779a螺旋槳模型為研究對象,采用Singhal全空化空化模型,在勻流場中比較了標準k-ω模型、修正Renormalization-group (RNG)k-ε模型和大渦模擬方法(LES)大渦模型對空化后螺旋槳推力系數和蒸汽體積分數的影響.其計算結果表明:標準k-ω模型能適應質量較低的非結構網格,穩定性較好,但對速度和湍流動能的預報精度不高;修正RNGk-ε模型對葉面隨邊處邊界層周圍黏性尾流產生的速度凹陷預報較為準確,對梢渦附近速度的預報也具有一定的精度.相比而言,LES在預報速度和湍流動能時比求解時均N-S方程的前兩種湍流模型更精確,但計算量更大,耗時更久.Liu等[6]同樣以E799a為研究對象,采用Schnerr-Sauer 空化模型,在勻流場中比較了標準k-ε湍流模型和非線性k-ε湍流模型對梢渦空泡的捕捉能力,其研究表明非線性k-ε湍流模型能夠有效預測梢渦空化.胡健等[7]采用LES和Schnerr-Sauer 空化模型,依然以E799a為研究對象,通過對螺旋槳葉梢附近處網格加密(網格單元數量近1 900萬),成功捕捉到勻流場中螺旋槳梢渦空化,數值結果與實驗結果吻合良好.劉芳遠等[8]采用RNGk-ε湍流模型和Zwart-Gerber-Belamri(Z-G-B)空化模型,對勻流場中PPTC(Potsdam Propeller Test Case)槳進行了空化數值計算,有效地實現了梢渦捕捉,同時指出水中含氣率對推力系數和轉矩的影響比空泡形態更強.
螺旋槳一般工作于非均勻流場中,上述的研究均是在均勻流場中進行的,并未對更加復雜的非均勻流場進行分析.Ji等[9]在非均勻流條件下,采用SSTk-ω湍流模型和Z-G-B空化模型對E799a螺旋槳空泡性能進行了數值分析,研究表明其數值計算葉背片空泡形態、空化體積與試驗結果吻合良好,但并未捕捉到梢渦空化.傅慧萍等[10]以PPTC槳為研究對象,結合RNGk-ε湍流模型和Z-G-B空化模型探究了斜流中螺旋槳的空化形態,但是其片空泡、梢渦空泡計算結果與試驗值略有差異.
本文以某油船槳為研究對象,基于RANS(Reynolds-averaged Navier-Stokes)方程,采用Schnerr-Sauer 空化模型和可實現的k-ε兩層湍流模型,采用商業軟件STAR-CCM+求解非均勻流場中螺旋槳的空泡形態,將計算得到的各相位角下葉背片空泡正投影面積、葉背片空泡形態及梢渦空泡形態與試驗結果進行對比.目標是求解出各相位角下與試驗相符的空泡形態,建立快速、高效、準確的空泡數值預報方法.
1 控制方程和空泡模型
在氣液兩相流混合模型中,流場被認為由可變密度的單一流質組成,忽略相間的速度滑移,氣相與液相具有相同的速度和壓力.在慣性直角坐標系下,定義坐標軸x為螺旋槳的旋轉軸,沿水流方向為正,見圖1.因此基于混合密度的均質混合流的連續性和動量控制方程為
(1)
(2)
ρm=ρvαv+ρl(1-αv)=ρvαv+ρlαl
(3)
μm=μvαv+μlαl
(4)
式中:下標i和j分別為坐標方向;下標 l、v分別指液相和氣相;t為時間;ρm為混合流密度;u和p分別為速度和壓力;μm為混合相的動力黏性系數;μt,m為湍流黏性系數;α為相體積分數.ρm和μm均通過體積加權平均后得到.采用可實現的k-ε湍流模型求解渦黏性系數,該模型適用于強旋轉流動和剪切流,文獻[2-5,7]采用該湍流模型得到了較為滿意的結果.
由于控制方程中增加體積分數這一未知量,因此需通過添加額外的方程進行封閉.相變過程可認為起始于溶解于水中的氣核,單位控制體積內混合流的質量始終保持不變,根據氣核的生長和潰滅速率可計算兩相間的質量輸運率和體積分數.基于Rayleigh-Plesset方程的Schnerr-Sauer空化模型能夠對氣液兩相間的質量輸運進行較好的描述[11].體積分數的控制方程為
(5)
(6)
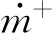
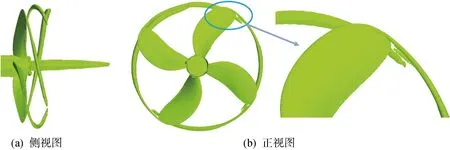
(7)
式中:p0為飽和蒸氣壓,取值 3 850 Pa,試驗時水溫為28.4 ℃.隨著空化逐漸發展,單位體積內汽泡個數N0=αln0,保證液相中汽泡密度始終保持不變.
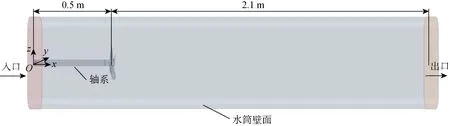
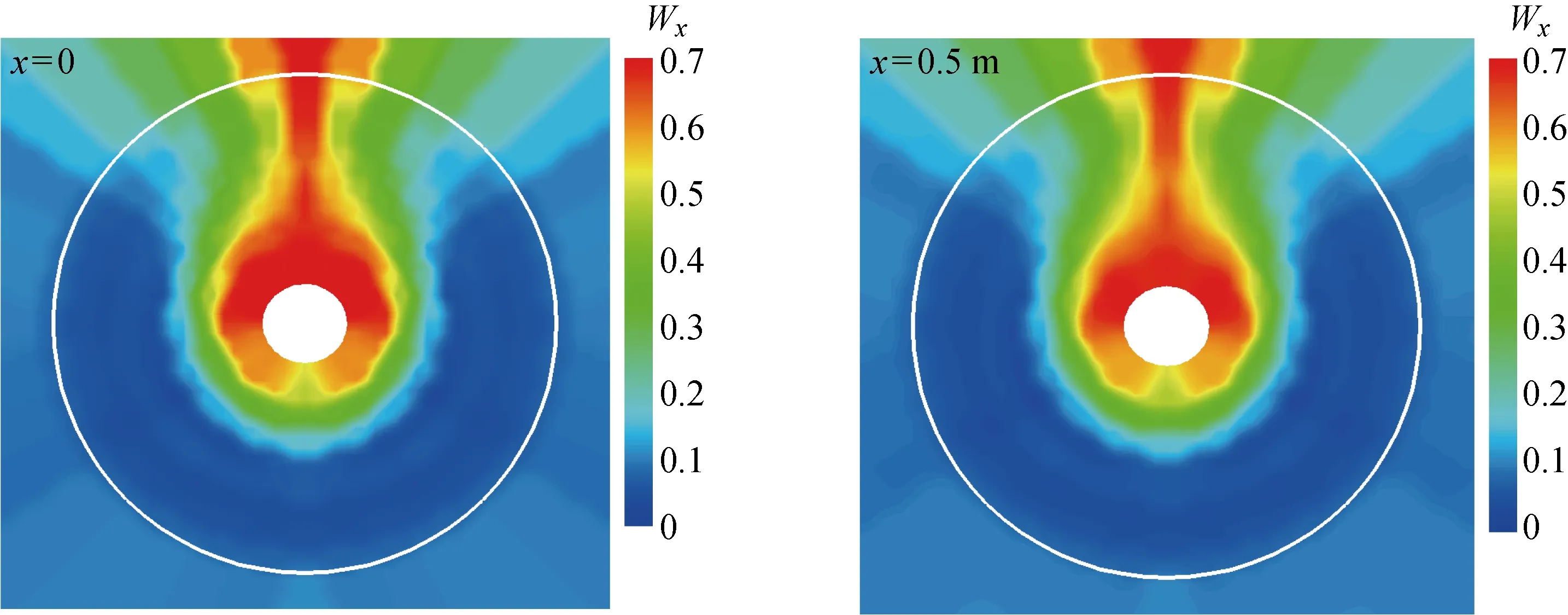
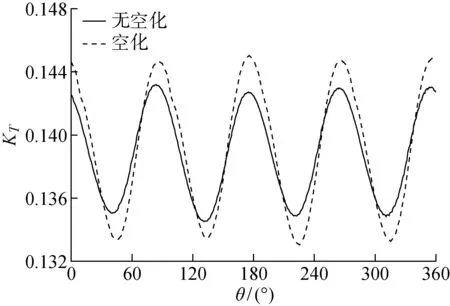
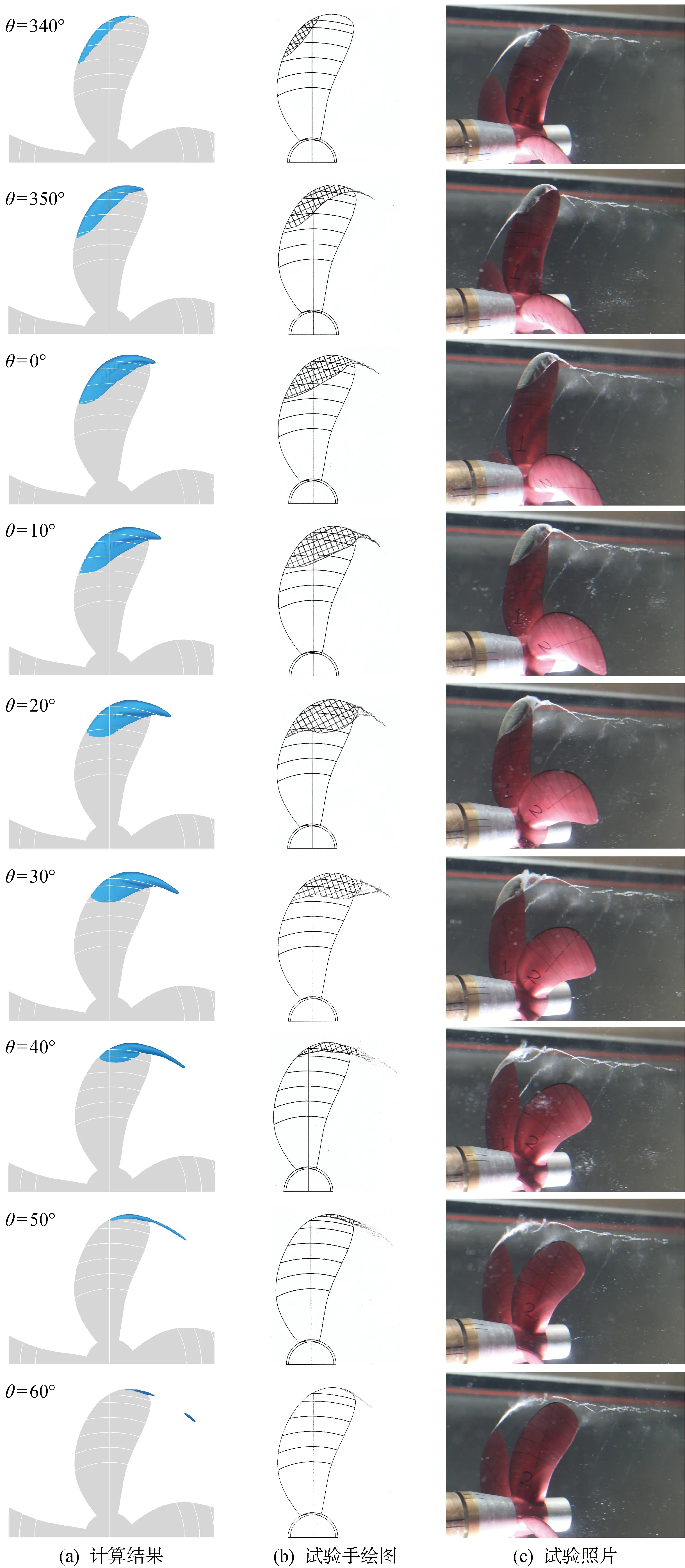
當p (8) 當p>p0時,氣體凝結,質量輸運速率為 (9) 本文以某萬噸級油船螺旋槳模型為研究對象,該槳模已在上海船舶運輸科學研究所(SSSRI)空泡水筒做過大量試驗[12].螺旋槳模型直徑(D)為248 mm,盤面比為0.4,螺距比(0.35D)為0.826,槳葉數為4,旋向為右旋. 計算區域與試驗條件完全相同,SSSRI空泡水筒工作段長2.6 m,橫截面呈正方形帶0.1 m倒圓角,寬為0.6 m,高為0.6 m,螺旋槳位于距入口0.5 m處,見圖1,原點坐標位于入口軸系中心處. 圖1 計算區域(m)Fig.1 Computational field (m) 網格采用六面體核心網格Trim類型,該模型內置有一個用以控制表面模板單元格尺寸的上限,這個上限可避免嚴重的模型幾何失真和生成質量差的網格.整個計算域分為靜止區域和螺旋槳旋轉區域,兩個區域通過交界面連接.為能捕捉到梢渦空泡,需對槳葉梢附近(渦量較大的區域)進行網格加密.渦量大小的判斷采用Q準則: (10) 圖2 Q等值面(Q=5×104 s-2)Fig.2 Isosurface of Q(Q=5×104 s-2) 式中:Ω為渦量;S為漩渦變形率,均為二階張量.圖2給出了Q等值面圖,從圖中可看出,螺旋渦管從槳葉導邊起始,由葉梢處脫出,與試驗梢渦空泡起始的位置相同.再進行空化流場計算時發現,當葉背片空泡產生時,由于片空泡具有一定的厚度,此時渦管在槳葉上的脫出位置與無空化狀態有所改變,產生向x軸負方向的微小位移.基于上述現象在對該渦管進行網格加密時,加密區域應包圍此渦管,為降低網格數量,僅對旋轉區域內螺旋渦管進行了加密. (1)靜止區域最大網格單元尺寸為0.08D,最小尺寸為0.008D(交界面網格尺寸).為保證槳盤面處伴流場,從入口至下游0.7 m處,以軸系為中心1.62D直徑范圍內進行網格加密,網格尺寸為0.02D,網格單元總數約為123 萬. 圖3 計算域網格(網格2)Fig.3 Mesh of computational field (mesh 2) (2)旋轉區域最大網格單元尺寸為0.008D,最小網格尺寸為0.002D(槳葉表面),槳葉設置為無滑移壁面,邊界層內第1層網格高度為2.76×10-4D,共6層,總厚度為4.03×10-4D,本文計算工況下漿葉表面無量綱法向距離y+均在30~100的范圍內.為捕捉梢渦空化,對槳葉梢及螺旋管進行網格加密,尺寸為0.001D,網格單元總數約為277 萬.網格劃分見圖3. 圖4 試驗測得的軸向伴流分布Fig.4 Distribution of axial wake measured by the test 為對計算結果進行可信性校驗,本文運用安全系數法[13]對3套網格計算得到的螺旋槳平均推力系數KT進行不確定度估算,KT=T/(ρln2D4)(T為螺旋槳推力,n為螺旋槳轉速).網格1、2、3計算得到的KT分別為 0.139 3、0.138 8、0.138 5,試驗值為 0.138 0,不確定度估算結果為4.464×10-4.分析計算結果可知,隨著網格數量的增加,推力系數逐漸降低且趨于試驗值,但是網格1與2、網格2與3以及網格3與試驗值之間的差異在變小.不確定度值相當小,可認為計算結果可信.圖5給出了不同網格計算得到的空泡形態.分析圖5可知網格1不能有效地捕捉梢渦空泡,網格2和3均能捕捉到梢渦空泡,葉背片空泡正投影面積和梢渦空泡形態一致.綜合考慮計算消耗和模擬精度之后,選用網格2進行后續計算. 圖5 不同網格模擬的空泡形態與試驗結果對比Fig.5 Comparisons of cavity pattern between calculation and test results at different mesh sizes 螺旋槳數值計算條件、工況與試驗條件完全相同[12].試驗中n為30 r/s,KT為0.138,背景壓力為pref,通過改變背景壓力滿足轉速空泡數σn=(pref-p0)/(0.5ρln2D2)=2.96.在正式計算之前,無螺旋槳情況下,需確認在速度進口處給定的流速分布,流向槳盤面位置時速度分布是否發生改變.圖6給出了入口處和槳盤面處的軸向伴流分布,分析圖6可知在槳盤面處流場分布與入口幾乎相同,因此可按該網格劃分方法進行后續計算. 為保證推力系數與試驗相同,又能捕捉到梢渦空化,因此先進行無空化流場計算.采用滑移網格方法,不加入空化模型,計算時間步長設定為 2.777 8×10-4s,對應螺旋槳旋轉角度為3°.背景壓力設置為1個大氣壓,調整來流速度(軸向伴流分布保持不變)直至時間平均推力系數相等.無空化狀態KT為 0.138 8,誤差為0.6%.螺旋槳旋轉一圈推力系數變化見圖7,分析圖7可知一個旋轉周期內推力系數出現4個峰值,與槳葉數相對應.由圖3可知從θ=45° 附近開始流場逐漸趨于均勻,推力系數曲線也在此出現波谷,無空化狀態波谷θ分別為40°、130°、220°及310°. 圖6 不同斷面處軸向伴流分布Fig.6 Distribution of axial wake at different cross-sections 圖7 螺旋槳旋轉一圈KT變化Fig.7 Variations of KT during one propeller rotation 當無空化流場計算穩定后,激活歐拉多相流模型和空化模型,調整環境壓力使轉速空泡數為2.96,計算時間步長為 9.259 26×10-5s,對應螺旋槳旋轉角度為1°.空化狀態KT為0.139,誤差為0.72%,推力脈動高于無空化狀態,最小推力系數出現在θ=45°,135°,225°,315°.為驗證數值計算結果的準確性,與試驗結果比較,對不同相位角槳葉空泡形態進行了對比分析,見圖8.采用αv=0.1等值面描述空泡形態.圖中給出了槳葉進、出伴流區域空泡發展及潰滅的整個過程:當槳葉開始進入伴流區域時首先出現葉背片空泡,起始于槳葉導邊附近,隨著槳葉繼續旋轉,葉背片空泡面積逐漸增大,梢渦空泡開始脫出,最大葉背片空泡面積出現在θ=10° 的位置,隨后片空泡面積逐漸減小,梢渦空化逐漸加強,隨著槳葉逐漸出伴流區域,葉背片空泡消失,梢渦逐漸降弱直至消失.數值計算準確的預測了這一歷程,片空泡初生、片空泡面積、梢渦初生及梢渦消失等現象與試驗結果吻合. 但是對于梢渦空化而言,空化形態略有差異,例如θ=60° 時,試驗照片顯示槳葉脫出的梢渦并不平滑,剛從葉梢梢部脫落時,梢渦非常細,隨后梢渦空化加強,渦管變粗且外圍呈現霧狀空化,渦管表面非常粗糙.這可能是由于梢渦脫出后進入高伴流區域,速度梯度變大,壓力非常不穩定,致使空化呈現出強烈的非定常特性,在短時間內劇烈變化.計算中θ=60° 時梢渦空化沿螺旋渦管也是由弱變強,從葉梢附近脫出、消失再出現,但是梢渦空間結構更加平順光滑.這主要是由于網格尺寸不能無限增加,再者RANS方法對該微小尺度渦不能夠準確預測.即使采用LES方法,其梢渦渦管依然平順[7]. 試驗中空泡手描圖能夠對葉背片空泡的大小、形態及穩定性進行詳盡描述,從θ=20° 開始梢渦在空間內呈現復雜的三維結構,手描圖難以在二維平面內對其準確的描述,對于梢渦形態手描圖僅進行了示意,因此僅對葉背片空泡進行了量化計算,分析了與試驗結果的差異性.現將不同相位角空泡計算結果、試驗手描圖和試驗照片進行圖像處理,每張照片均進行圖像重塑為正投影圖片,分別測繪葉背空泡正投影平面面積和槳葉正投影平面面積.定義葉背片空泡面積百分比γ=AS/AB(AS為葉背空泡面積,AB為槳葉面積).表1給出了數值和試驗葉背片 表1 計算和試驗葉背片空泡面積對比Tab.1 Comparisons of back-sheet cavity area between calculation and test results 圖8 不同θ時空泡形態計算結果與試驗結果比較Fig.8 Comparisons of cavity pattern between calculation results and test results observation at different θ values 空泡正投影面積百分比結果,分析表1可知數值計算結果與試驗結果吻合,僅在θ=40° 時相差5%左右,其他情況下計算結果與試驗結果的差值在2.5%以內. 本文以較少的網格數量成功模擬了非均勻流場螺旋槳葉背片空泡和梢渦空泡.結果表明:Schnerr-Sauer空化模型和可實現的k-ε兩層湍流模型能夠對非均勻流場螺旋槳空泡形態進行準確預測,計算結果與試驗結果吻合,該計算方法可為非均勻流場螺旋槳空泡模擬提供參考.2 研究對象、網格劃分及可信性校驗
2.1 研究對象
2.2 網格劃分及可信性校驗
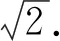
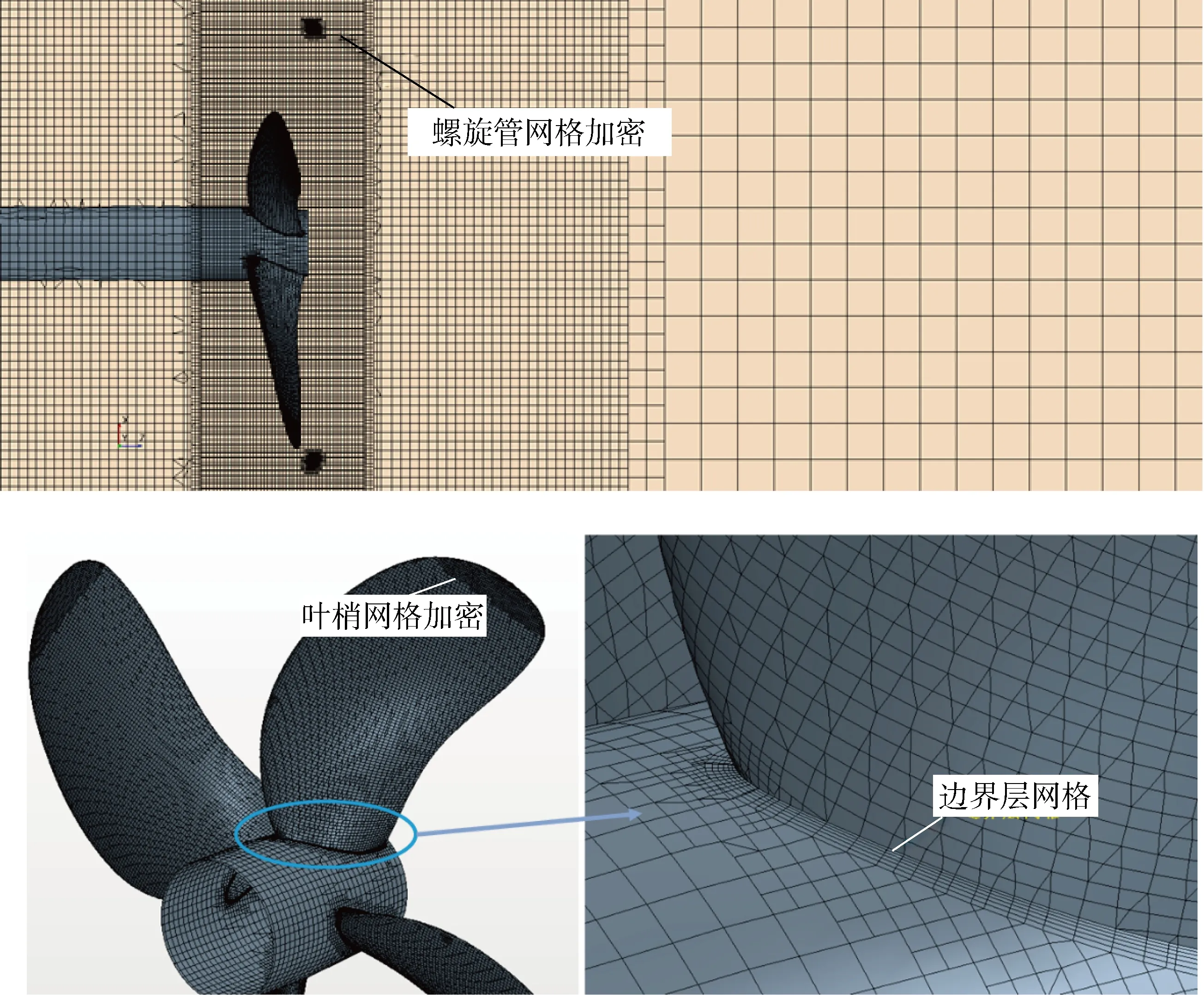
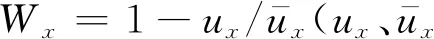
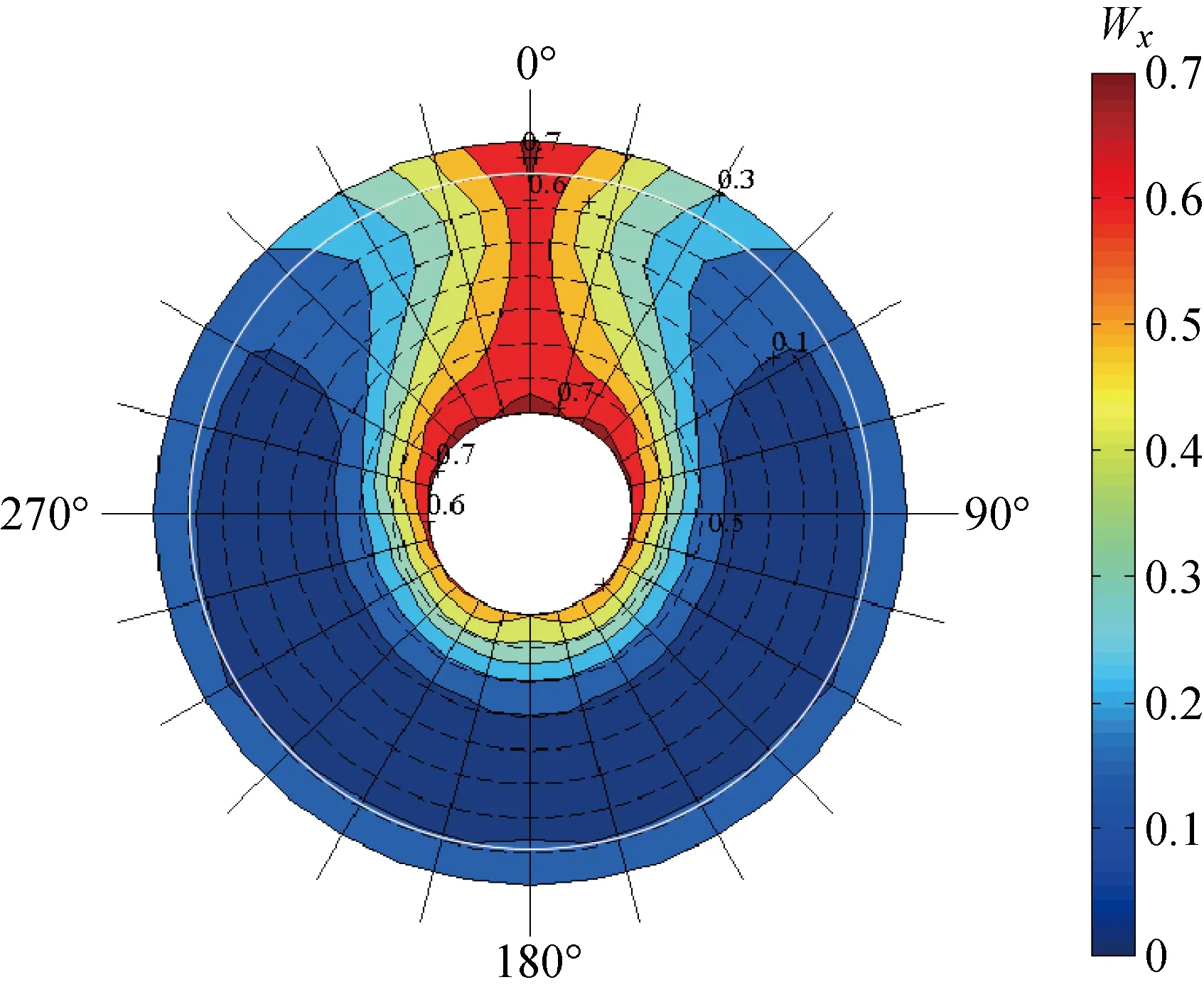
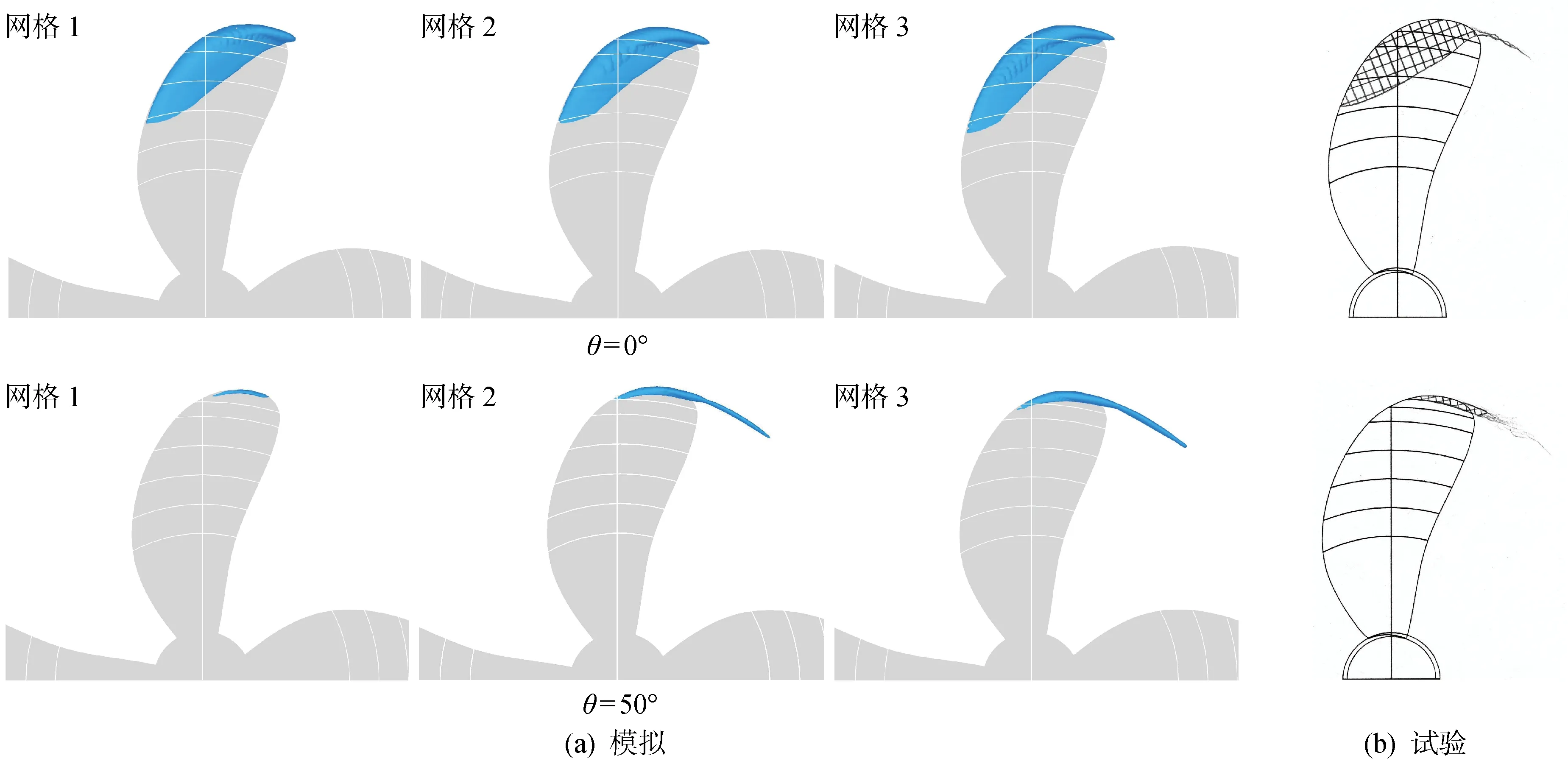
3 結果分析
3.1 無空化流場數值模擬
3.2 空化流場數值模擬

4 結語

