低弗勞德數通氣超空泡初生及發展演變特性

許海雨，羅 凱，黃 闖，左振浩，古鑒霄

(西北工業大學 航海學院，西安 710072)

超空泡減阻技術通過生成包裹航行器的超空泡，避免了大部分航行體表面直接沾濕，從而實現航行阻力的顯著減小和航行速度的大幅提高[1].通氣超空化問題受到國內外研究學者的高度重視.通氣超空泡通常分為兩種泄氣模式：回射流泄氣和渦管泄氣.前者通常發生在弗勞德數較大、重力因素可忽略的情況下[2]，后者通常出現在弗勞德數較低，重力對超空泡流型影響較大的情況下[3-4].眾多學者研究得到了雙渦管泄氣超空泡與回射流泄氣超空泡的轉變條件[5].

Skidmore[6]在試驗中發現航行器模型在小尺寸水洞中空泡以雙渦管模式泄氣，而在大尺寸水洞中空泡以回注射流模式泄氣.Karn等[7]通過試驗研究了不穩定來流對超空泡形態及泄氣方式的影響，指出閉合區泡內外壓差是引起空泡泄氣方式轉變的原因.Rashidi等[8]通過水洞試驗及數值仿真方法研究了通氣超空泡的回射流現象，捕捉到空泡內氣體向空化器方向流動，并發現空泡內有明顯氣體旋渦.王志等[9]采用離子圖像測速(PIV)技術對通氣超空泡內氣體流動結構開展研究，發現了3種典型的空泡流動結構并對每種結構的成因進行了分析.Wang等[10]采用試驗與數值模擬相結合的方法建立了通氣超空化數值模型，模擬了渦管泄氣和回射流泄氣超空泡，并對其流動結構開展了研究.張孝石等[11]在水洞中開展了通氣量對航行體云狀空泡穩定性影響的試驗，指出通氣量影響空泡演變過程，通氣量增大導致空泡發展周期增大，空泡脫落尺寸減小.Ahn等[12]在兩種不同水洞設備中對比分析了相同工況下的超空泡外形及尺度的變化規律.Cao等[13]采用歐拉多相流模型研究了雙渦管泄氣超空泡的空化特性，得到了空泡形態及泡內壓力隨通氣率、流速的變化規律.鄧飛等[14]在水洞試驗中研究了雙圓盤空化器的超空泡形態變化特性，指出雙圓盤空化器存在前盤優先誘導空泡生成及后盤誘導空泡生成兩種空化狀態.Xiang等[15]對通氣超空化流動特此開展數值仿真研究，得到了空泡閉合區氣體體積分數、氣泡速度及氣泡尺寸的分布特性.

綜上，上述研究均集中于發展充分的雙渦管泄氣或回射流泄氣超空泡形態及流場特性，缺少對超空泡初生及發展過程中空泡演變特性的研究，特別是關于在空泡發展過程中空泡形態及泄氣方式的動態變化特性研究.本文基于分相流模型和SST湍流模型，建立可壓縮通氣超空化數值模型.在通氣率和弗勞德數(Fr)系列變化范圍內，系統地研究兩種超空泡的生成及發展演變過程，重點分析了空泡生成過程中空泡形態及泄氣模式的變化規律.

1 計算方法

1.1 數值方法

1.1.1控制方程 商用流體計算軟件CFX的多相流模型包含勻質平衡流模型和分相流模型，文獻[13]分析了兩種多相流模型對通氣超空化的影響，指出分相流模型在計算通氣超空化上具有較高的計算精度.

通氣介質為常溫空氣，忽略兩相間換熱，因此能量方程可以忽略，控制方程只涉及連續性方程、動量方程及體積分數方程.

連續性方程為

(1)

式中：γα為α相(1為水相，2為氣相)的體積分數；ρα為α相的密度；ui為速度；i和下文j分別表示坐標方向；t為時間.

動量方程為

(2)

式中：p為靜壓；μ為動力黏度；Mi為相間作用力.

1.1.2湍流模型 基于Baseline (BSL)k-ω模型的SST湍流模型考慮了湍流剪切應力的傳輸，可以精確地預測流體流動的開始和大逆壓梯度條件下的流體分離.因此本文采用SST湍流模型，基本方程為

(3)

(4)

式中：ρ為密度；k為湍流動能；μ為流體動力黏度；μt為渦黏度系數；pk為湍流生成率；ω為湍流頻率；σω2、σω3、σk3、α3、β3和β′為模型常數.

(5)

(6)

(7)

式中：ν為運動黏度；y′為到最近壁面的距離.

1.1.3算法配置 本文采用有限體積法離散控制方程，控制方程的瞬態項及擴散項分別采用二階向后歐拉式和中心差分格式進行離散，此外，控制方程的對流項采用高精度格式離散方法以提高計算精度.采用全隱式多網格耦合求解技術，同時求解連續性方程、動量方程及能量方程等控制方程，可進一步提高計算收斂速度.為了節約時間，獲得合理空泡演變規律，對非定常計算的時間步長進行無關性分析，最終確定時間步長為0.1 ms.

1.2 物理計算模型

1.2.1計算模型 為了在水洞試驗中驗證數值方法的準確性，本文采用兩套計算模型，一套為水洞試驗驗證的細直桿模型；一套為研究通氣空泡生成、發展的數值計算模型.為了減小模型對通氣超空泡流型的影響，水洞試驗采用細直桿模型，如圖1(a)所示.數值計算模型為了清晰捕獲空泡生成及發展過程中的空泡形態演變特性，減少模型對其影響，采用單空化器模型，如圖1(b)所示.

圖1 幾何模型Fig.1 Geometric model

1.2.2計算域及監測位置設置 通氣超空化區伴隨空泡脫落及強湍流度，因此需要劃分足夠精細的計算網格，對整個計算域進行結構化網格劃分，其中60%以上的網格分布在兩相空化區.并對計算網格進行網格無關性檢驗，網格數為80萬.計算域左側邊界采用速度入口，計算域右側邊界采用壓力出口，通氣孔采用質量流量入口邊界條件，通氣為可壓縮常溫空氣.計算域周圍采用無滑移壁面邊界條件.為了研究超空泡內壓力的變化特性，分布選取P1和P2作為監測點，以監測流場壓力時變特性，其距離空化器的位置分別為2dc和7.5dc，其中dc為空化器直徑.如圖2所示，圖中x為超空泡發展方向，y為重力反方向，來流速度分3種工況：5 m/s、7 m/s及9 m/s.

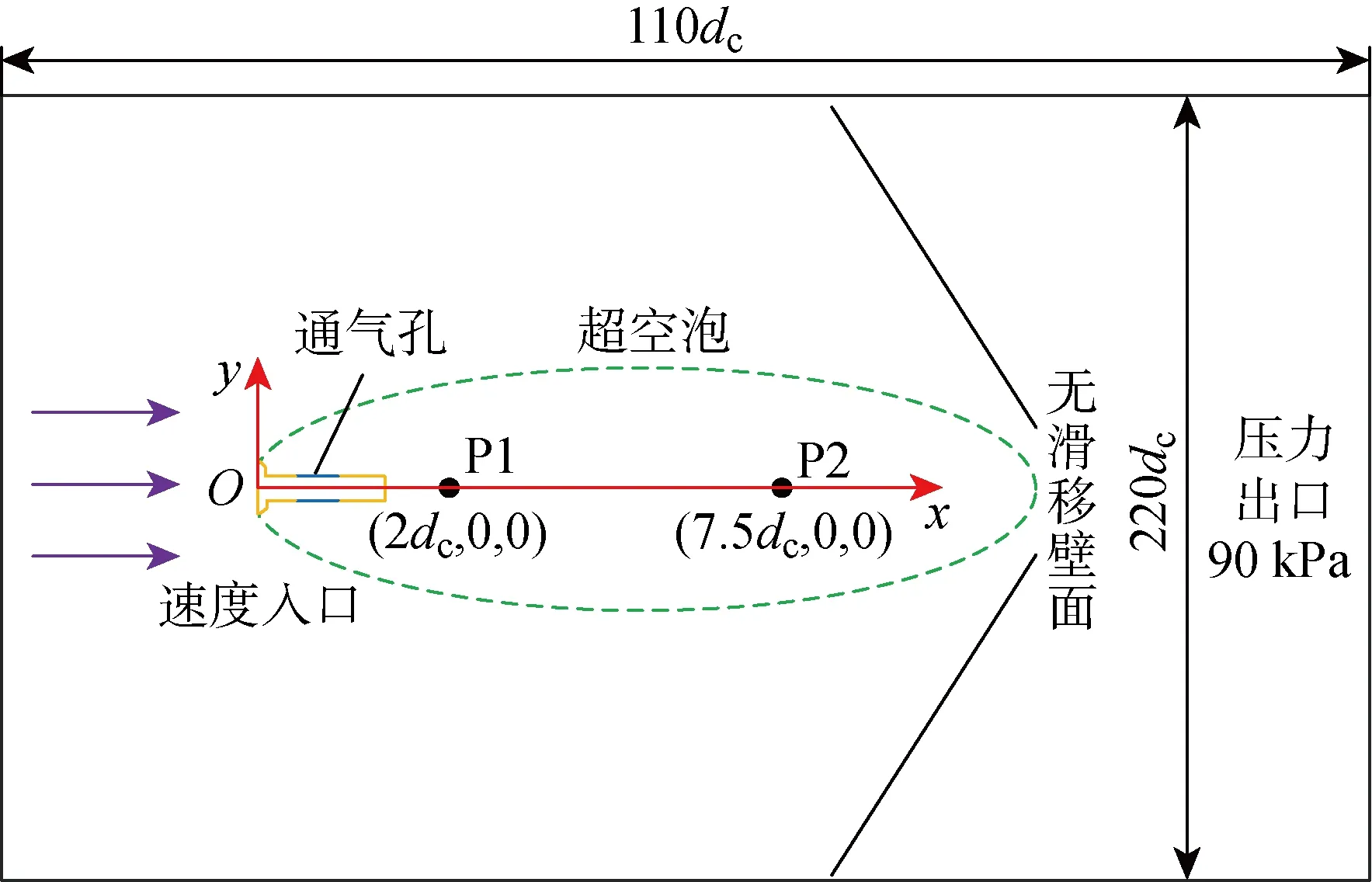
圖2 流域及邊界條件Fig.2 Flow domain and boundary conditions

1.3 模型驗證

為了評估仿真結果的置信度，在西北工業大學水洞中開展用于數值計算方法驗證的水洞試驗，數值仿真采用與試驗相同的計算工況.圖3給出了兩種通氣率下數值計算與水洞試驗的空泡形態結果對比，圖中：Lmax為空泡最大長度；Dmax為超空泡最大直徑；Cq為通氣率.兩種工況的弗勞德數相同，均為24.8，Cq定義如下：

(8)

式中：Q為超空泡氣體體積流量；v為來流速度.

可以看出，在小通氣率工況下，數值計算得到的超空泡最大直徑與水洞試驗結果誤差約為2.82%，超空泡最大長度與水洞試驗結果誤差為2.75%.大通氣率工況下，數值計算得到的超空泡最大直徑與水洞試驗結果誤差約為2.65%，超空泡最大長度與水洞試驗結果誤差為2.66%.為了進一步驗證所建立數值模型的計算精度，圖4給出了在兩種通氣率下數值計算得到的不同時刻超空泡最大長度與水洞試驗的對比結果.由圖可知，小通氣率時，超空泡隨時間發展迅速，空泡長度增長較快，隨后空泡發展緩慢，超空泡長度的增長率顯著減低，最后超空泡發展穩定，超空泡最大長度幾乎不隨時間改變.這是由于開始時超空泡以回射流方式發展，空泡發展迅速，當流動時間為0.9 s時，空泡泄氣方式轉變為雙渦管泄氣方式，由于一部分氣體從渦管流出空泡體，因此空泡的發展緩慢.數值仿真可以精準模擬空泡的發展演變特性，并且在不同時刻下空泡尺度與試驗結果吻合度較高.在大通氣率下，本文所建立的數值模型仍可以高精度地模擬通氣超空化的演變特性，在不同時刻空泡長度與試驗誤差的最大值為2.4%.綜上所述，本文所采用的數值計算方法可以有效地揭示通氣超空化流動機理，空泡尺度與尾部泄氣方式與試驗結果符合度較高，這說明本文的計算方法有較高計算精度，可用于通氣超空泡生成及演變特性的研究.

圖3 Cq不同時數值仿真與水洞試驗結果比對Fig.3 Comparison of test and numerical results at different Cq values

2 計算結果及分析

空化數σ及弗勞德數Fr兩者決定了通氣超空泡的泄氣類型，而通氣率是影響空化數的最主要參數之一.因此本文選用通氣率及弗勞德數兩個參數變量研究通氣超空泡泄氣轉變特性.

2.1 通氣率對空泡初生及發展演變特性的影響

為了研究通氣率對超空泡泄氣類型的影響，本文在通氣率從小到大范圍內，選擇一系列通氣率開展空泡初生及發展演變特性研究，發現隨著通氣率的增大，超空泡泄氣模式依次為回射流泄氣、空泡泄氣轉變臨界狀態及雙渦管泄氣.為了對比研究3種泄氣類型空泡的初生及發展演變特性，文中分別選擇代表3種典型空泡泄氣方式的通氣率(Cq=0.03，0.06，0.39).

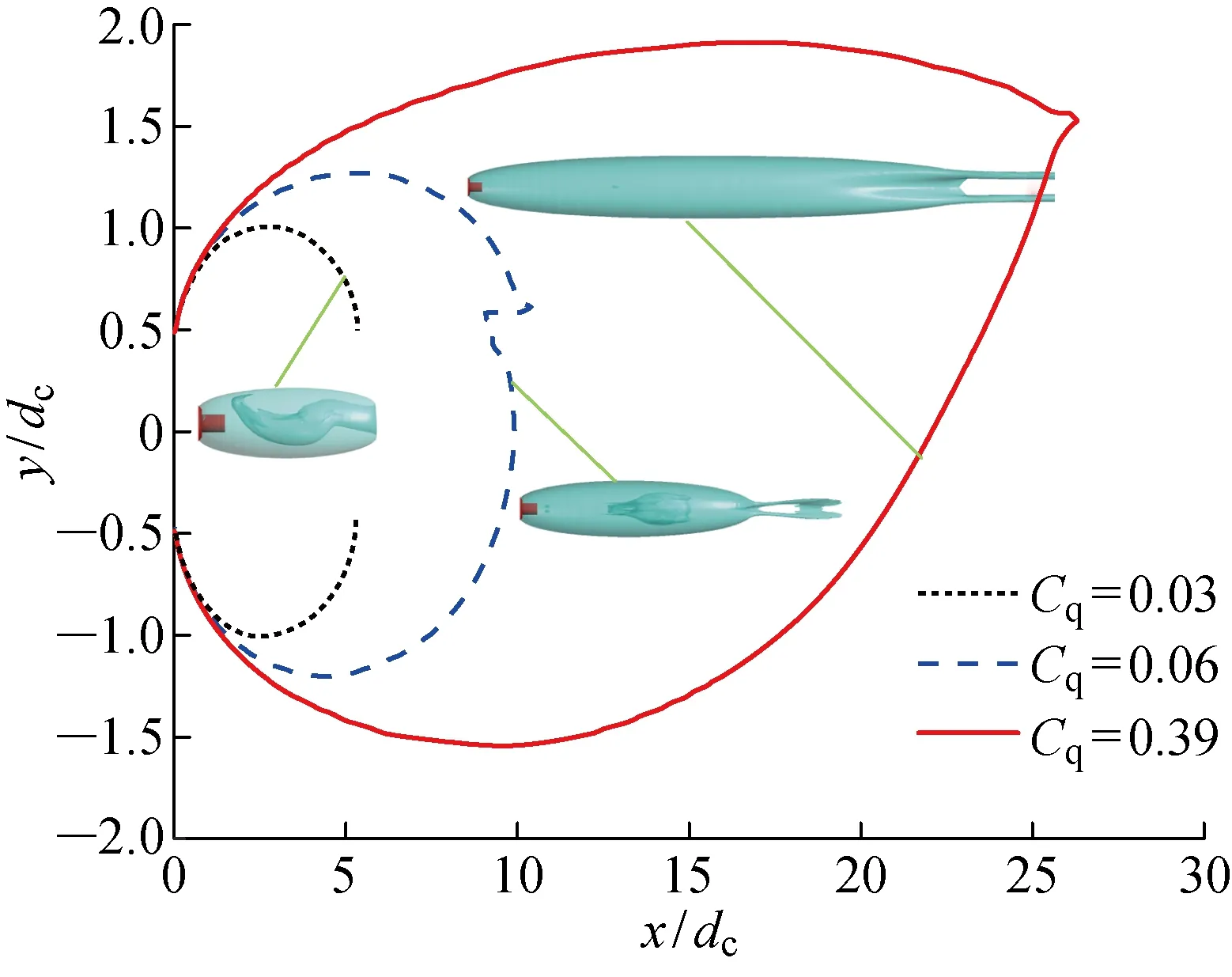
圖5 不同Cq下超空泡輪廓線Fig.5 Supercavity profiles at different Cq values

圖5給出了超空泡對稱面上的空泡輪廓曲線.由圖可知，隨著通氣率的增加，超空泡整體幾何尺寸增大，并且重力對空泡形態的影響也越來越顯著.通氣率為0.03時，空泡形態較小，空泡長度為5.1dc，并且空泡幾何形態為軸對稱空泡，幾乎不受重力效應影響，超空泡以回射流模式泄氣.通氣率增加到0.06時，空泡尺寸顯著增大，空泡長度為10.38dc，超空泡泄氣模式為雙渦管泄氣，但渦管形態較小.當通氣率增加到0.39時，空泡長度增加到26.3dc，超空泡流型受重力影響更大，空泡幾何中心線向上彎曲更顯著，空泡為非對稱幾何形態，此時超空泡以雙渦管模式泄氣.

圖6給出了通氣率為0.03時的超空泡初生、發展及泄氣模式演變過程.由圖可知，在空泡剛生成(t=0.04，0.08 s)時，空泡發展非常不穩定，出現了空泡氣團的斷裂、分離現象.隨著空泡的進一步發展，空泡斷裂現象逐漸消失，但空泡形態具有較強的非定常特性.超空泡泄氣模式為回射流泄氣，在空泡閉合區通入的非凝結氣體裹挾液體水流向空化器方向，并且在閉合區周期性地發生空泡氣團的脫落與空泡的再發展，空泡氣團脫落主體空泡后空泡尺寸減小，然后再繼續發展變大.例如t=1.62 s時刻空泡氣團脫落，空泡長度為46dc，當t=1.66 s時，空泡長度增大到55dc.當t=1.76 s時，空泡氣團再次脫落，空泡長度減小到47.5dc.

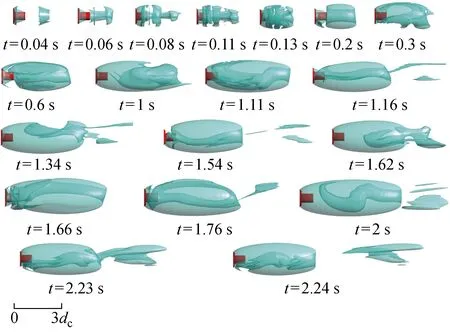
圖6 Cq=0.03時超空泡發展過程Fig.6 Development of supercavity at Cq=0.03

圖7為空泡內壓力振蕩特性，圖中pc為空泡內壓力.在空泡初生時，P1和P2位置的壓力先開始逐漸增大，最大壓力分別為97.1 kPa，99.3 kPa.這是因為超空泡剛發展時，監測點位于空泡閉合區后，其壓力受到超空泡閉合區的高壓影響.隨著空泡的進一步發展，當監測點位于空化區時，泡內壓力開始減小，但由于回射流現象導致空泡內壓力振蕩，空化數發生改變，因而空泡形態及尺度也相應改變.當空泡發展充分時，P1位置的壓力振蕩幅度為3.3%，而P2位置壓力振蕩更加劇烈，振蕩最大幅度為13.3%，其原因在于通氣率過小，空泡形態較小，P2正位于空泡閉合區附近，因此壓力振蕩顯著.由空泡形態及壓力特性可知，回射流超空泡非常不穩定，難以預估其空泡形態及尺寸.

圖8為Cq=0.06時通氣超空泡生成及發展演變過程.圖中將超空泡在重力方向投影所得空泡形態作為正視圖，正視圖中空泡尾部出現的管狀形態即為雙渦管泄氣模式，這可以從圖中最后一行給出的俯視圖中看出.通氣超空泡在剛生成時空泡形態表現出強烈的非定常特性，空泡以回射流模式泄氣.空泡發展非常不穩定，仍出現了空泡氣團的斷裂、分離現象(t=0.04 s).隨著空泡的進一步發展，空泡逐漸增大，在空泡閉合區因回射流強度及回流方向具有時變性，當氣/水混合物與空泡輪廓相互接觸時，空泡形態被破壞，呈現出形態各異的超空泡流型(t=0.18,0.32,0.48 s).超空泡在發展充分時空泡泄氣方式在回射流泄氣和渦管泄氣兩者之間交替進行，回射流泄氣空泡形態如圖中t=1.62,2.10 s所示.渦管泄氣空泡形態如圖中t=2.00,2.32 s所示.

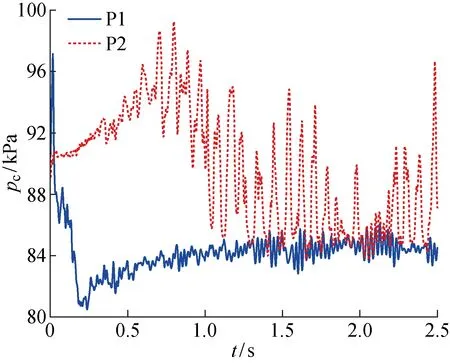
圖7 Cq=0.03時空泡內壓力振蕩特性Fig.7 Oscillation characteristics of pressure inside supercavity at Cq=0.03

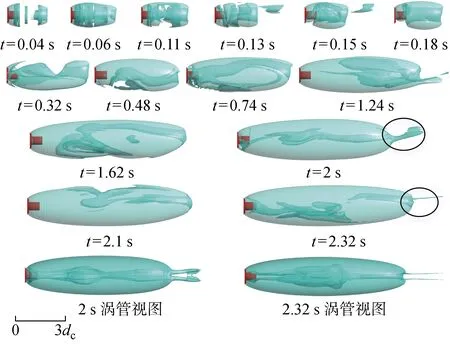
圖8 Cq=0.06時超空泡發展過程Fig.8 Development of supercavity at Cq=0.06

空泡內壓力振蕩特性如圖9所示.由圖可知，空泡內壓力發生一定程度的振蕩，并且P2位置的壓力振蕩更為劇烈.按照Campbell-Hilborne空泡泄氣轉變經驗判斷準則，σFr<1時，空泡以雙渦管模式泄氣；當σFr>1，空泡以回射流模式泄氣.由于空泡內壓力持續振蕩，空泡內壓力處于最大時，計算得到的σFr=0.96，當空泡內壓力處于最小時，σFr=1.58.因此空泡泄氣模式不穩定，在回射流泄氣和渦管泄氣之間來回轉變.

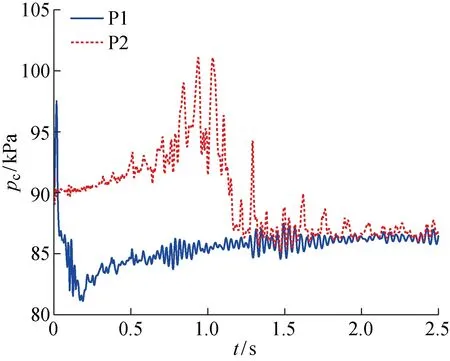
圖9 Cq =0.06時空泡內壓力振蕩特性Fig.9 Oscillation characteristics of pressure inside supercavity at Cq=0.06

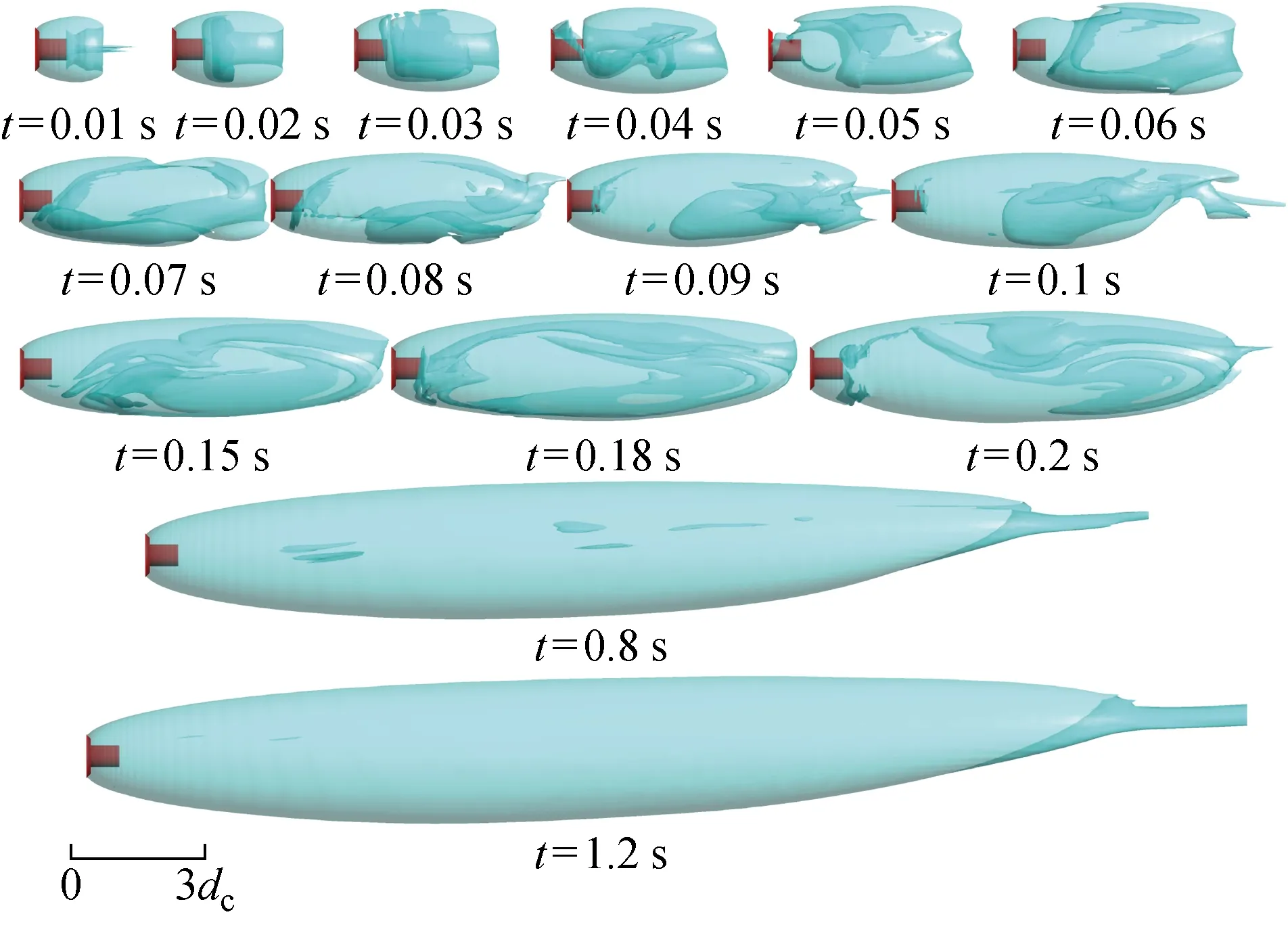
圖10 Cq=0.39時超空泡發展過程Fig.10 Development of supercavity at Cq=0.39

圖10為Cq=0.39時空泡生成及發展演變過程，由圖可知，通氣超空泡在剛生成時空泡發展速度較快.相比較于Cq=0.06的工況，在相同時刻時，超空泡尺度更大，發生空泡形態分離、斷裂等現象減少，并且空泡發展速度更快，表明增大通氣率抑制了空泡的破裂，有助于超空泡的生成及發展.超空泡開始先以回射流泄氣方式生成及發展，如圖中t=0.18 s之前的空泡形態.隨著空泡的繼續發展，空泡幾何尺寸增大，受重力效應的影響也越來越顯著，超空泡泄氣模式最后轉變為回射流模式泄氣(t=0.8，1.2 s).

圖11為空泡發展過程中泡內壓力振蕩曲線，由圖可知，開始時空泡內壓力振蕩劇烈，超空泡非定常特性強烈，這是由于空泡受到回射流作用導致的.當t>0.8 s時，空泡內壓力振蕩特性減緩，空泡最大壓力振蕩幅度僅為344 Pa，此時超空泡以雙渦管模式泄氣，這表明相比較于回射流泄氣，雙渦管泄氣超空泡更加穩定，空泡內壓力及空泡形態非定常性較弱.當超空泡以雙渦管泄氣時，空泡內無回射流現象，通入氣體沿著空泡壁向下發展，在空泡閉合區從雙渦管流出空泡體.

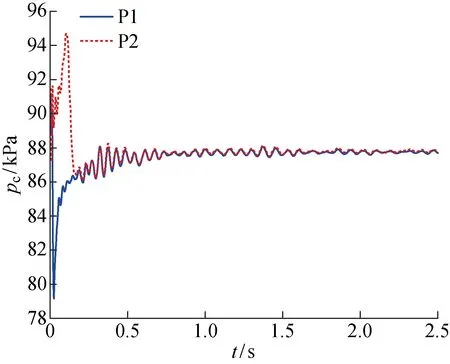
圖11 Cq=0.39時空泡內壓力振蕩特性Fig.11 Oscillation characteristics of pressure inside supercavity at Cq=0.39

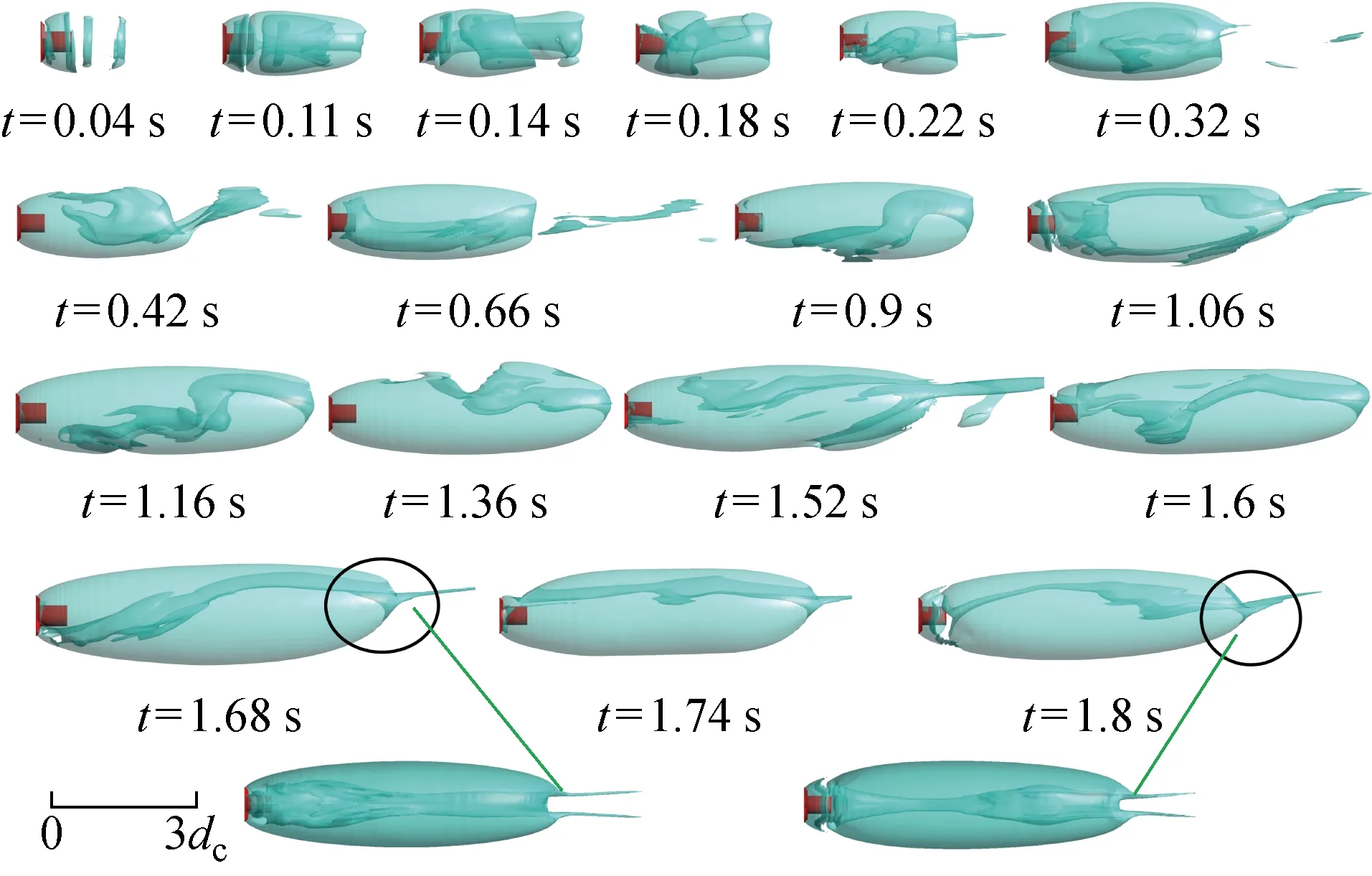
圖12 Fr=11.3時超空泡發展過程Fig.12 Development of supercavity at Fr=11.3

2.2 Fr對超空泡生成及發展演變特性影響

本文選用Cq=0.06，Fr=15.8超空泡泄氣轉變臨界狀態作為參考點，通過增大和減小Fr，以獲得其對超空泡泄氣模式轉變的影響特性.因此保持通氣率0.06不變，系列改變Fr(分別取11.3、20.3)，以研究其對通氣超空泡泄氣類型的影響特性.圖12為Fr=11.3時的空泡演變過程，在空泡開始生成及發展過程中，空泡主要以回射流泄氣模式發展，其空泡演變特性與Fr=15.8時的工況相同，但發展過程中出現渦管泄氣次數更多(t=1.06，1.52 s).當空泡充分發展時，空泡泄氣方式轉變為雙渦管泄氣，如圖中最后一行所示.此時雙渦管管徑較小，但空泡內部仍存在回射流現象，即空泡尾部氣/水混合物流向空化器方向.

空泡內壓力振蕩特性如圖13所示.當空泡泄氣類型轉變為雙渦管泄氣時，空泡內壓力最大振蕩幅度為690 Pa，相比于通氣率0.39時工況，壓力振蕩幅度增大，這也表明空泡內回射流現象的存在.通氣率0.39時，空泡形態較大，因此受重力效應影響大，泄氣方式完全轉變為渦管泄氣，并且空泡內氣體完全從兩個渦管泄出.而Fr=11.3工況空泡形態較小，空泡未全部轉變為渦管泄氣，因此渦管管徑較小，泡內存在回射流動.

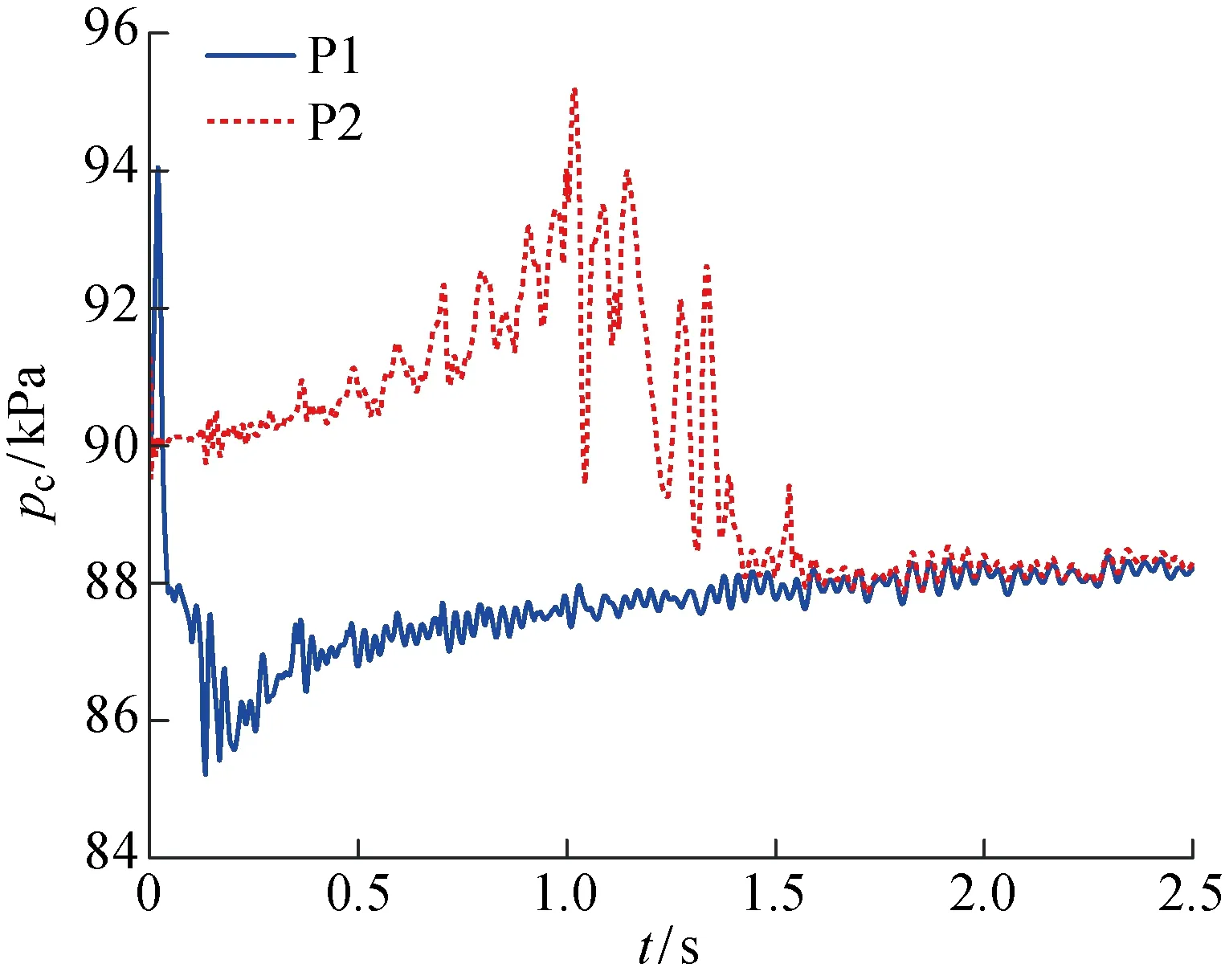
圖13 Fr=11.3時空泡內壓力振蕩特性Fig.13 Oscillation characteristics of pressure inside supercavity at Fr=11.3

圖14為Fr=20.3時的通氣超空泡生成、發展及泄氣特性圖.由圖可知，Fr增大時，通氣超空泡泄氣模式為回射流泄氣，超空泡在生成及發展過程中，回射流對空泡輪廓造成的破壞減小，并且空泡發展速度更快.相比于Fr=15.8工況，超空泡渦管泄氣模式消失，在整個發展過程中，超空泡始終以回射流方式泄氣(t=2.37，2.40，2.50 s).另外，P2位置的壓力要高于P1位置的壓力，這表明空泡內壓力并非恒定的，具有非均勻特性，泡內壓力沿空泡發展方向逐漸增大.

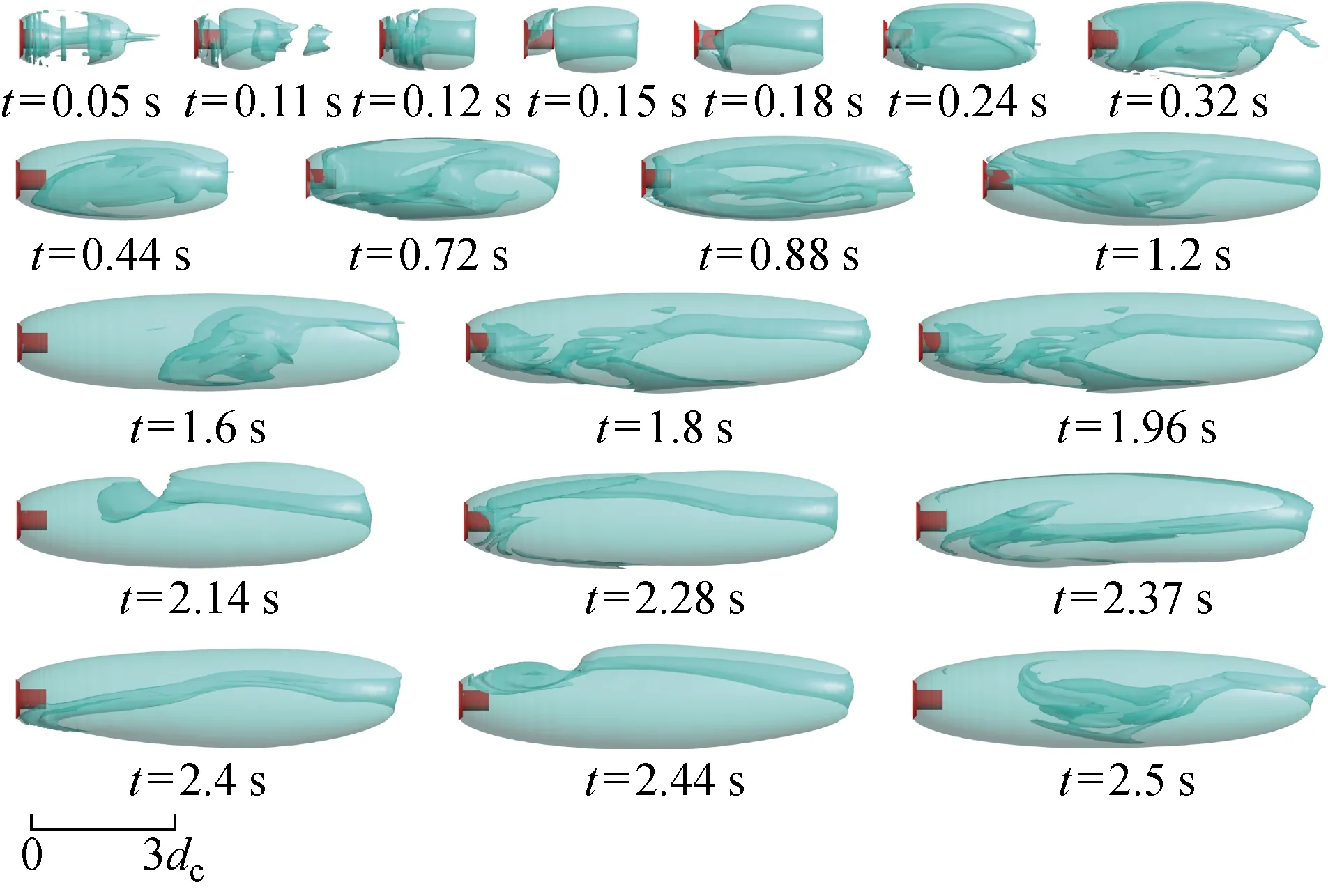
圖14 Fr=20.3時超空泡發展過程Fig.14 Development of supercavity at Fr=20.3

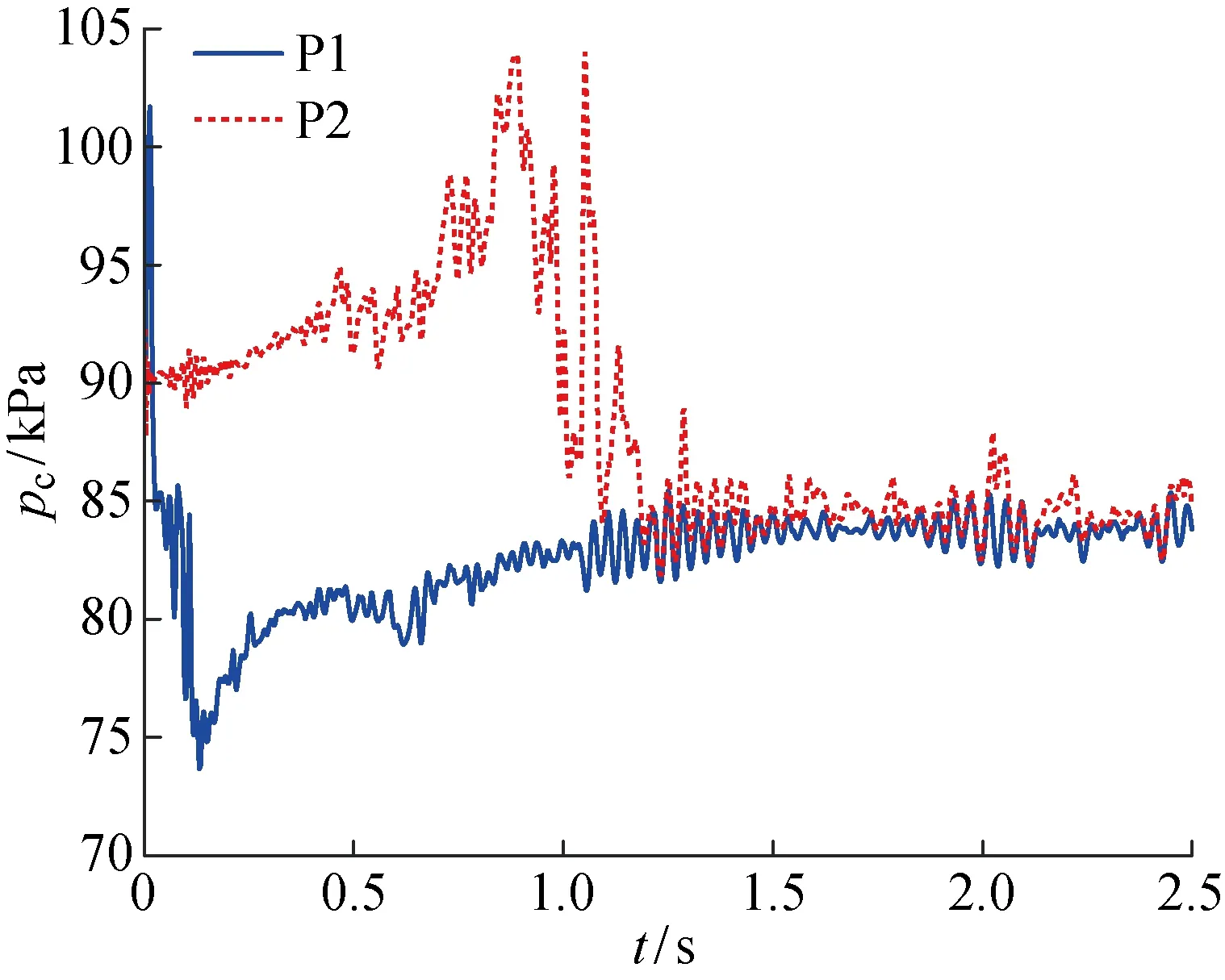
圖15 Fr=20.3時空泡內壓力振蕩特性Fig.15 Oscillation characteristics of pressure inside supercavity at Fr=20.3

空泡內壓力時變特性如圖15所示.相比于低速工況，當超空泡發展完全時，Fr增大，空泡內壓力振蕩特性增強，壓力振幅及振蕩周期均顯著變大，這與空泡回射流泄氣及泡內流動結構有關.通氣率為0.03時空泡泄氣方式為回射流方式，空泡內壓力振蕩更加猛烈.由此可知，回射流超空泡內壓力具有振蕩特性，并且增加流速有助于抑制回射流泄氣超空泡的壓力振蕩.

3 結論

本文對回射流泄氣及雙渦管泄氣的空泡生成、發展及空泡形態變化特性進行非穩態數值計算研究，重點對比分析了不同泄氣類型空泡的形態變化規律及泄氣模式之間相互轉變特性，得到以下結論：

(1)回射流泄氣超空泡內存在氣體裹挾水反向流動的回射流，空泡尾部伴隨氣團的周期性脫落，在空泡初生時伴隨空泡的斷裂及分離現象，空泡形態難以預估，泡內壓力振蕩劇烈.

(2)雙渦管泄氣超空泡相對比較穩定，空泡形態及泡內壓力變化幅度較小，空泡初生時先以回射流模式泄氣發展，隨著空泡進一步發展，最終空泡泄氣模式轉變為雙渦管泄氣.

(3)當空泡處于或接近空泡泄氣轉變臨界時，空泡在初生時以回射流模式泄氣，當空泡充分發展后空泡泄氣類型一直在渦管泄氣和回射流泄氣之間相互轉變，流場及空泡形態變化特性更加復雜.