空間兩剛體滾動約束系統在線運動規劃
任書鋒,楊 丹,余海東,王 皓,b
(上海交通大學 a.上海市復雜薄板結構數字化制造重點實驗室;b.機械系統與振動國家重點實驗室,上海 200240)
機械手靈巧操作和球形機器人的規劃控制是機器人研究領域的熱點,涉及到與物體的接觸與滑動接觸,純滾動接觸能量損耗小,構成一類非完整系統[1],可使用較少的驅動器實現靈巧操作,有利于降低成本并提高系統可靠性.然而,系統狀態變量之間難以解耦帶來了控制和規劃上的困難,同時,滾動約束系統不能轉為鏈式結構,不具備微分平坦的良好特性,且該系統不滿足冪零條件[2],無法使用相關的控制算法.因此,建立一種可以用于實際機器人系統的滾動約束運動規劃方法十分重要.
國內外學者對于非完整系統的研究主要可分為基于最優化的方法和增量隨機采樣的方法.前者通過構造目標函數和非線性約束,將運動規劃問題轉換成非線性優化問題,代表方法有打靶法、直接配點法、迭代線性二次調節器(iLQR)和最優動作控制(SAC)[3-6].其中,直接配點法通過設置配點將運動規劃問題轉換為非線性規劃問題,對初始狀態量和控制量的取值不敏感,算法較為穩定.iLQR將非線性系統線性化,然后使用梯度下降的方法,迭代計算得到最優軌跡.SAC算法可以實現快速在線運動規劃.增量隨機采樣方法的代表為快速搜索隨機樹(RRT)[7]及其改進算法.例如:RRT*,Bi-RRT和Goal-bias RRT等,基于采樣的方法具有效率低、規劃路徑不連續的缺點,同時對于非完整約束,基于控制狀態空間采樣的方法可能導致不收斂,而基于運動狀態空間采樣的方法在擴展子節點時仍需解決兩點邊值問題[8].
滾動約束系統運動規劃方法按照接觸模型可分為針對球-平面間的滾動接觸模型的控制方法[9-12],如冪零近似迭代驅動[9]、基于高斯-博內定理的分階段控制方法[10]和基于同倫延拓法[11]的數值優化方法.針對兩個球之間滾動接觸模型的控制方法,文獻[13]利用球的運動封閉性質提出了球在一般三維物體上滾動的運動規劃算法,文獻[14]提出了球與具有恒定曲率物體滾動接觸的控制方法,文獻[15]將球-平面模型運動規劃方法拓展到高維球體在高維歐式空間中.上述研究成果針對某一特定模型建立,并且都沒有考慮實際機器人系統中的在線控制,這些方法通過離線一次性完成運動規劃,如果應用到實際機械系統的實時控制,由于計算效率的問題,重新計算的控制輸入可能已經不適用于當前狀態.
針對已有研究成果的局限性,本文建立了滾動約束系統的實時運動規劃算法,分別選取常見的球-平面模型和球-球模型作為仿真對象,通過傳感器的反饋更新系統狀態,使用滾動優化的方式滿足對實時規劃的要求,同時改進了SAC算法中滾動預測的迭代方法,以適用于系統變量高度耦合的滾動約束系統.另外,結合球-平面模型和球-球模型的仿真模擬,驗證了算法對這兩類常見滾動約束機器人系統的有效性.
1 滾動約束運動學模型
1.1 接觸模型坐標系系統
兩個剛體點接觸模型如圖1所示,圖中:Oxsyszs為整體坐標系;Ox1y1z1、Ox2y2z2分別為固連在兩個剛體上的正交坐標系;Oxc1yc1zc1、Oxc2yc2zc2分別為接觸點在物體1、2上的正交坐標系;nc1、nc2分別為物體1、2上接觸點坐標系的法向量;ψ為接觸點處坐標系Oxc1yc1zc1和Oxc2yc2zc2之間的相對轉角,將坐標系Oxc2yc2zc2繞著坐標系Oxc1yc1zc1的n軸轉動ψ角度后,兩坐標系的x軸重合.在Oxc2yc2zc2中定義2個物體間的相對線速度V=[vxvyvz],相對角速度Ω=[ωxωyωz].

圖1 接觸模型坐標系Fig.1 Coordinate system of contact model
建立三維物體曲面W?R3的參數表達式,存在二維平面上的開子集U?R2到該曲面W的一個可逆坐標映射f:U?R2→W?R3,使用(u,v)表示該二維平面參數坐標,定義(f,U)為曲面W的參數化表達,對于球面的正交坐標系可為
f:U→R3:(u,v)
(ρsinucosv,ρsinusinv,ρcosu)
(1)
式中:ρ為球半徑;0 基于正交坐標系,定義曲面上某一點f(U)處的單位高斯坐標系為 (2) 兩個三維剛體滾動接觸運動模型如圖2所示,考慮空間物體1受到與物體2的距離為ρ1+ρ2(ρ1為物體1Ox1y1z1到Ox1y1z1的距離;ρ2物體2Ox2y2z2到Oxc2yc2zc2的距離)的約束,因此物體1相對于物體2有5個自由度,該位形空間可用q=[u1v1u2v2ψ]5個參數表示,并使用U1=[u1v1]表示接觸點在物體1曲面上的位置,U2=[u2v2]表示接觸點在物體2曲面上的位置. 圖2 空間剛體滾動接觸運動模型Fig.2 Model of rolling contact motion for space rigid bodies 根據文獻[16]的結果,2個三維物體純滾動的一階運動學方程為 (3) 同時,保持兩物體接觸的約束條件為 vz=0 (4) 兩物體間純滾運動的約束條件為 vx=0,vy=0,ωz=0 (5) 式(3)可表示為如下的控制仿射形式: (6) 式中:t為控制時間;q(t)為系統狀態變量;c(t)=[-ωyωx]T為系統控制輸入. (7) 非完整系統的運動規劃問題可以轉換為最優控制問題:尋找滿足非完整約束式(6)的一個最優c*(t)(t∈[0,T],T為控制結束時間),并滿足起終點狀態約束: q(0)=qstart,q(T)=qgoal (8) 式中:qstart為起點的位形;qgoal為終點的位形. 同時使如下二次型性能指標函數為極小: (9) l(q(t),c(t))=0.5[q(t)-qd(t)]T× Q(q(t)-qd(t))+0.5c(t)TRc(t)dt (10) m(q(T))=0.5[q(T)-qd(T)]T× P1[q(T)-qd(T)] (11) 式中:m[q(T)]為對終點狀態偏差的權重;Q為動態軌跡跟蹤偏差的半正定權重矩陣;qd(t)為通過離線規劃獲得的參考軌跡;R為系統控制能量輸入的正定權重矩陣;P1為計算與目標點偏差的半正定權重矩陣. 除起終點約束外,對于三維空間流形,需要解決奇異點的問題,一種可行的方法是用多個坐標映射構建一個圖冊.為簡化問題,通過引入不等式約束避免奇異點,例如對式(1)中球面參數坐標系在極點位置u=0和u=π存在2個奇異點,可設置如下約束: 0 (12) 同時,對兩物體的相對角速度幅值c建立如下約束: cmin≤c≤cmax (13) 式中:cmin為最小控制輸入向量;cmax為最大控制輸入向量. 為簡化表達,使用ξ(t)代表(q(t),c(t)),上述最優控制問題可表示為如下形式. 輸入:物體曲面模型、qstart及qgoal. 輸出:滿足式(8)、(12)及(13)約束且使性能指標函數式(9)最小的最優c*(t)(t∈[0,T]),即 (14) 式中:h(ξ(t))包括式(6)非完整約束和式(8)起終止狀態約束方程;g(ξ(t))包括式(12)的奇異點約束和式(13)的控制變量約束方程. 針對上述建立的最優控制問題,建立如圖3所示的在線控制算法框圖,實現系統的在線控制,圖中c1為名義控制輸入. 圖3 在線控制算法框圖Fig.3 Online motion planning algorithm 第一階段為離線運動規劃,使用配點法快速獲得名義軌跡.將運動規劃過程分為N-1段,每段兩端節點稱為配點,子區間表示為[ti,ti+1],i=0,1,2,…,N-1,hi=ti+1-ti表示區間時長,使用qi代表ti時刻的系統狀態.對每個區間,采用多項式樣條描述軌跡,使用辛普森積分求解運動微分約束方程和成本函數的積分來平衡對計算效率和精確度的要求.具體實現方法如下: (15) 式中:c0~c3為多項式系數. 同時在區間端點處滿足: (16) 式中:fi為式(7)中非線性方程在第i點計算得到的當前接觸點位形速度. 求解式(15)和(16)構成的線性方程組,可以獲得c0~c3的表達式,并將t=(ti+ti+1)/2代入式(15),獲得區間中點的狀態變量的表達式為 (17) 使用辛普森積分計算性能指標函數: (18) 在每個子區間上使用辛普森積分計算非完整約束: (19) 式(18)中li+1/2和(19)中fi+1/2均為式(17)中點狀態qi+1/2的函數. 因此,式(14)表達的系統離線運動規劃問題可以表示為如下的非線性規劃問題: s.t.h(q(ti)∶q(tN);c(t0)∶c(tN-1))=0 g(q(ti)∶q(tN);c(t0)∶c(tN-1))≤0 (20) 針對上述非線性規劃問題,使用與目標軌跡的距離作為性能指標,為獲得軌跡最短的優化結果,使用初始點和目標點間的線性插值作為配點法的目標軌跡. 在使用配點法優化軌跡時,迭代初值的選取對最終的求解結果有很大影響,在實際應用中,常對5個狀態變量軌跡有不同要求,例如球形機器人在平面滾動,期望平面上的接觸點軌跡最短,而對球面接觸點軌跡和物體間相對轉角軌跡要求滿足起終點約束即可,應選擇使得平面上接觸點軌跡為直線的控制輸入作為配點法的初始值.圖3中兩狀態控制法的目的即是通過控制5個系統狀態中兩個狀態軌跡為起終點間線性插值,使用式(3)反向求解獲得對應的控制輸入ctc(t).具體實現方法如下: (21) 式中:[1]、[2]分別表示提取q的第1、第2個元素. 由式(3)的第1個方程可得: c(ti)=[K1(ti)+Rψ(ti)K2(ti)Rψ(ti)] (22) 由式(3)的其余兩個方程,使用歐拉法得到其余3個狀態變量軌跡的計算公式為 RψK2(ti)Rψ]-1c(ti) (23) 從i=0,1,2,…,M-1交替使用式(22)和(23)得到c(ti)和q(ti),獲得兩狀態控制下的軌跡qtc(t)和控制輸入ctc(t). 使用兩狀態控制法的結果ξtc=[qtcctc]作為初始值,求解式(20)的非線性規劃問題,可以獲得維度為5(N+1)優化軌跡qdc矩陣和維度為2(N+1)的控制輸入cdc. 首先將非線性模型式(6)線性化: (24) 式中: 在預測區間內,最優控制律可以表達為 (25) 對應的系統狀態變量求解形式為 q(t)= (26) 式中:f1(s)=f[q(s)c1(s)],f2(s)=f[q(s)c2(s)]. 構建預測區間內運動規劃的二次型函數J1: (27) (28) (29) (30) 式中:η(t)為梯度方向;ε為步長.由此得 (31) (32) (33) 式中:Jτ為關于時間的單變量函數.使Jτ最小的控制介入時間即為最優控制介入時間τ. 步驟3通過線搜索迭代求解最優控制時長λ: λ=ωkΔtinit (34) 式中:ω為搜索速率;k為迭代次數;Δtinit為控制時長的初值.將獲得的最優控制律作用在[t0,t0+ts],在獲得反饋更新后,根據反饋結果更新狀態,重新計算預測窗口內的最優控制律并應用到下一個采樣周期內,直到控制任務結束. 基于上述建立的滾動約束系統在線規劃算法,通過MATLAB軟件實現球-平面模型和球-球模型的仿真,仿真程序運行環境為:i7-4770MQ CPU@3.40 GHz 12 GB RAM.規劃周期均設置為1 s,使用序列二次規劃(SQP)算法實現非線性規劃問題式(20)的求解,獲得參考軌跡和名義控制輸入,在實時運動規劃過程中應用四階龍格庫塔法求解非完整約束式(7). 離線規劃中配點法使用表1中的參數,配置41個配點,設置相應的控制變量幅值約束,對Q,P1和R的選取主要考慮軌跡與起終點直線軌跡qd的動態跟蹤誤差最小,因此使用較大的Q和較小的R,P1用于增加目標點的權重,可根據對不同系統變量的要求在對角線位置選擇不同的數值. 使用表2中的參數作為在線運動規劃的仿真參 表1 滾動接觸模型離線運動規劃參數Tab.1 Parameters for offline planning of rolling contact model 表2 滾動接觸模型在線運動規劃參數Tab.2 Parameters for online planning of rolling contact model 數,模擬反饋控制頻率為50 Hz,設置預測時間窗口為0.5 s,求解式(7)預測模型運動,并將模擬結果作為傳感器的反饋輸入.表中kmax為迭代次數的最大值. 在真實系統中,應建立具有可控性的滾動約束模型,對于滾動約束非完整系統的可控性,已有學者進行了相關研究.文獻[17]給出任意兩個空間三維物體滾動約束系統可控性的一般性結論:當且僅當兩個物體的曲面空間是非等距同構時,任意兩個空間三維物體滾動約束系統是完全可控的. 應用上述結論,在任意模型參數下,球模型和平面模型是非等距同構的,因此球-平面滾動接觸模型是完全可控的.對于球-球接觸模型,當且僅當兩球的半徑不同時,兩個球為非等距同構,因此需要建立不同球半徑的接觸模型,即ρ1≠ρ2. 對于球在平面滾動的運動規劃仿真,標記平面模型為物體1,標記球模型為物體2,使用式(1)作為球參數表達式,選擇球半徑ρ=0.5.設置起點位形為qstart=[π/4 0 π/2 0 0],目標點位形為qgoal=[π/2 π/2 π/2 0 0]. 圖4所示為該仿真案例中,滾動接觸模型在t=0,0.25,0.75,1 s時刻的狀態,并標注兩個物體上接觸點的最終優化軌跡.對比起終點位置處球模型上固連坐標系的狀態,證明球面接觸點的位置[u2v2]以及ψ保持一致,圖中灰色平面表示接觸平面,紫色球體表示運動過程中的接觸球體. 圖4 球-平面滾動接觸運動規劃結果Fig.4 Planning results of sphere-plane rolling contact motion 圖5所示為球-平面模型仿真結果,模型的5個位形坐標在t=0.9 s附近提前達到預定的目標位置,圖例中qg(i)(i=1,2,…,5)表示目標點的5個位形坐標,其中球面接觸點軌跡構成一條閉合曲線以滿足起終點位置相同的要求,并且軌跡上的箭頭標明了球面接觸點閉合軌跡的運動方向.由于離線規劃采用低階的方法求解非完整約束方程,所以獲得的參考軌跡在真實機器人系統中并不能滿足非完整約束,而在實時控制中采用高階方法求解約束獲得的軌跡與真實系統更加接近,因此離線與在線規劃結果存在一定差異,同時在線規劃中通過調整預測窗口長度的方式可以快速得到下一采樣區間的優化控制輸入,并在獲得新的反饋后修正結果,不斷滾動迭代. 圖5 球-平面模型優化控制輸入和狀態空間曲線Fig.5 Optimized control input and state space curves of sphere-plane model 圖6 球-平面模型計算時間曲線Fig.6 tc versus t of sphere-plane model 圖6所示為球-平面模型的每步的計算時間tc與仿真時間(即前文控制時間)的關系,在該案例中,計算時間為6.5~8.9 ms,單步平均求解時長為7.1 ms.在仿真中,采樣時間為20 ms,考慮到使用MATLAB軟件計算效率較其他編譯型語言低,建立的控制器可用于中低速運動的場景. 對于球在另一個球面滾動的運動規劃仿真,標記半徑較大的球模型為物體1,另外一個球模型為物體2,設置兩個球模型的半徑參數分別為ρ1=4,ρ2=1,同樣使用式(1)作為球參數表達式.設置起點位形為qstart=[π/4 0 π/2 0 0],目標點位形為qgoal=[π/2 π/4 π/2 0 0]. 圖7所示為該仿真案例中,滾動接觸模型在t=0,0.25,0.75,1 s時刻的狀態,并顯示兩個物體上接觸點的最終優化軌跡,終點處物體2上接觸點位置與起點處相同,并且達到物體1上的目標位置. 圖8所示為球-球模型仿真結果,5個位形坐標在t=1 s時刻達到預定的目標位置,由于對物體1上接觸點參考軌跡設置的權重較大,在線規劃的最終軌跡與物體1上的參考軌跡有較高的重合度. 圖7 球-球滾動接觸仿運動規劃結果Fig.7 Planning results of sphere-sphere rolling contact simulation motion 實際上,如果SAC算法直接使用起終點的線性插值作為目標軌跡,會出現無法到達目標點的情況,因此離線規劃的目的是為在線規劃提供一條較好的參考軌跡,使得在線規劃每一次滾動優化的目標值都具有一定可行性,并且離線規劃可以根據實際情況調整配點數量和積分方法平衡參考軌跡的精度和計算時間. 圖9所示為球-球模型的每步的計算時間與仿真時間的關系,在該案例中,計算時間為6.7~13.0 ms,單步平均求解時長為8.1 ms,計算效率較球-平面模型低. 圖8 球-球模型優化控制輸入和狀態空間曲線Fig.8 Optimized control input and state space curves of sphere-sphere model 圖9 球-球模型計算時間曲線Fig.9 Calculation time curve of sphere-sphere model 本文基于純滾動接觸運動學模型,構建了含滾動約束這一類非完整系統的在線運動規劃算法框架.針對已有的研究成果受限于特定的模型且提出的算法只適用于離線的、全局的運動規劃的問題,改進了SAC算法,采用離線運動規劃結合在線運動規劃的方式,建立了通用性更強的在線運動規劃算法.通過配點法快速獲得低精確度的參考軌跡,在實時規劃過程中通過反饋校正和滾動優化獲得下一步的優化控制輸入.將算法用于球-平面模型和球-球模型的仿真,結果證明該算法可用于解決球形機器人地面運動控制和機械手指操作物體的實時運動規劃問題,也為其他滾動接觸機器人系統的控制算法提供了可行的解決方案.1.2 滾動約束運動方程


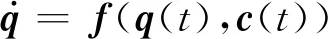
2 滾動約束運動規劃算法
2.1 問題的描述


2.2 運動規劃算法
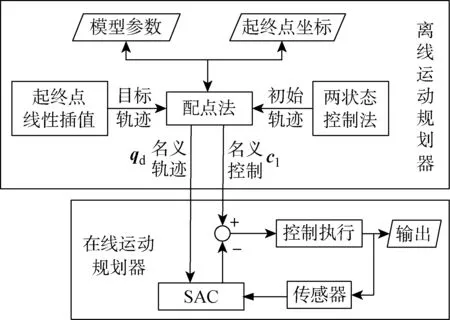










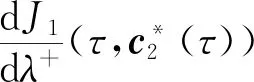
3 仿真計算及結果分析
3.1 仿真參數


3.2 滾動約束系統的可控性
3.3 球-平面接觸模型運動規劃仿真
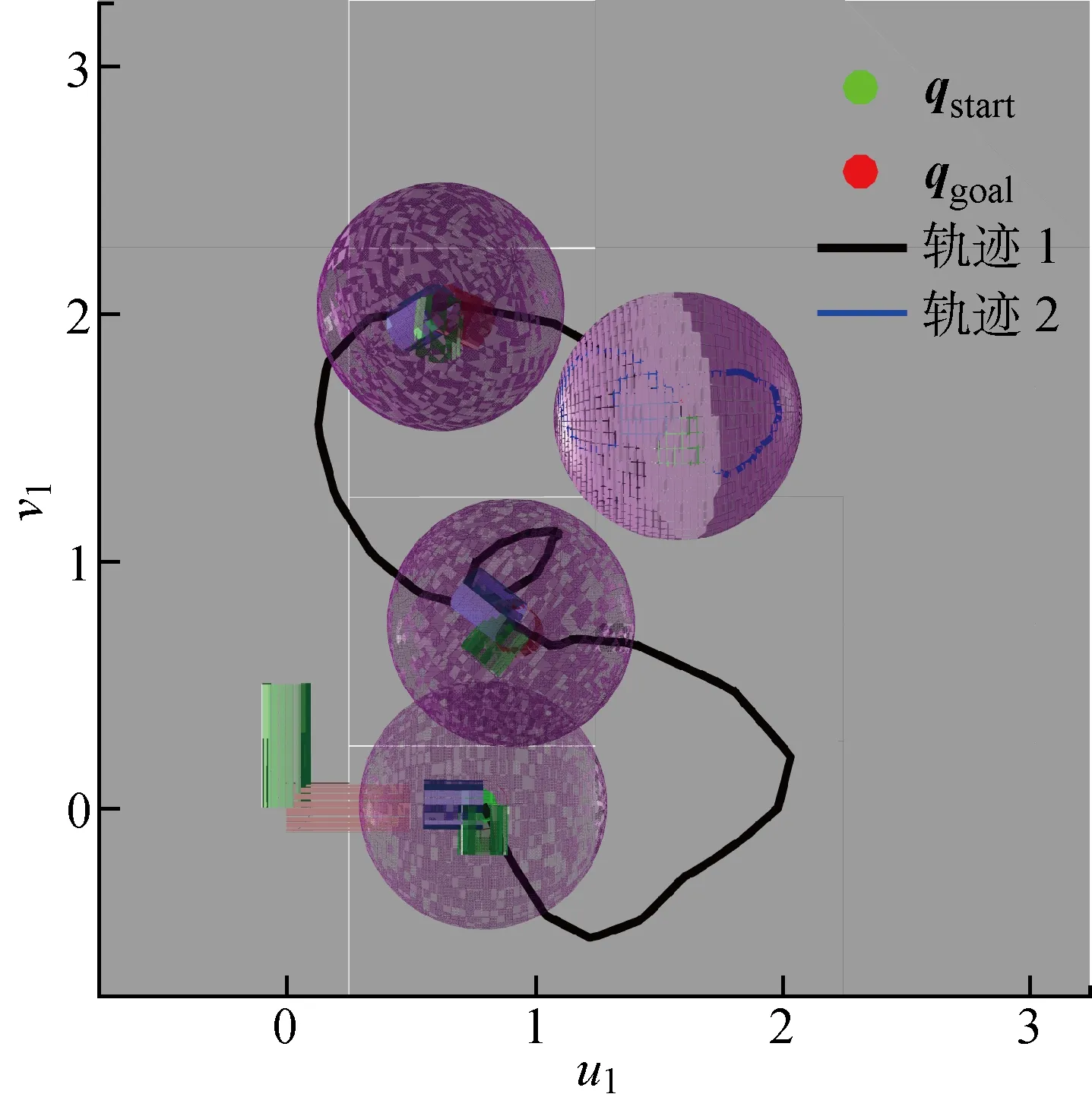


3.4 球-球接觸模型運動規劃仿真



4 結語

