一個多參數優化系統在簡單模型中的應用

祖子清，楊慶，夏江江，張蘊斐，朱學明

（1.國家海洋環境預報中心自然資源部海洋災害預報技術重點實驗室，北京 100081；2.中國科學院東亞區域氣候-環境重點實驗室，中國科學院大氣物理研究所，北京 100029）

1 引言

相對于自然界真實的大氣和海洋的狀態變化，數值預報總是伴隨著預報誤差。誤差來源可分為初始誤差和模式誤差[1]。初始誤差是因為數值模式使用了不準確的初始條件，而初始條件的準確程度會受到觀測系統的空間布局以及觀測儀器精度等因素的限制[2-4]。模式誤差是由于數值模式對自然界真實狀態演變過程的描述存在不合理之處，這取決于模式的差分方案、物理過程的參數化方案[5]以及模式使用的物理參數值等是否合理[6-7]。

對于模式誤差，合理選取模式物理參數的取值，可以在一定程度上抵消模式誤差[8-9]。在調整參數時常用的方法是手動調整，即給定一個參數值，然后積分模式，考察模擬是否更加靠近觀測，然后根據這一信息繼續更新參數值。這種方法往往運算量大，且具有主觀性和片面性。因此，人們發展了多種數學方法對模式參數進行調整，如基于集合卡曼濾波的方法[10-13]、基于四維變分的方法[14-15]和基于粒子濾波的方法[16]等。

四維變分同化是一種有效的調整模式參數的方法[17-19]。該方法定義目標函數衡量同化窗口內模擬的狀態變量與觀測序列的距離，采用變分（伴隨）方法搜索使距離縮小的方向，利用優化算法不斷更新物理參數值，最終使狀態變量不斷趨近于觀測序列。Zhang等[20]采用伴隨方法和孿生試驗，對三維正壓潮汐模式中的二維底摩擦系數進行了優化。Peng等[21]利用伴隨方法，針對風暴潮預報中較為關鍵的物理參數（如拖曳系數）進行了優化，結果表明通過同化觀測數據，參數的調整可以抵消部分模式誤差（不論這部分模式誤差是否由于拖曳系數的誤差所致），顯著提升風暴潮增水預報能力。Zhang等[22]利用四維變分方法估算了海洋邊界層模式中的兩個參數。但是，這種方法的缺點是優化系統設計復雜、需要數值模式具備伴隨模式、可移植性差。

本文發展了一個多參數優化系統。該系統設計簡單，便于移植，采用直接計算梯度的方法，不需要數值模式事先具有伴隨模式，適用于數值模式中少量參數（少于10個）的優化問題。在孿生試驗的假定下，本文基于一個理想的模型，開展了3個參數的優化試驗。本文首先介紹使用的模型和方法，然后介紹試驗結果，最后進行總結和討論。

2 模型和方法

2.1 模型簡介

本研究使用了盒子模型進行參數估計。盒子模型是為研究北大西洋經圈翻轉環流的穩定性和多平衡態等性質而發展的一個模型[23-25]。盒子模型較為簡單，包括兩個方程，3個物理參數，沒有空間格點，方程如下：

式中：T和S分別為海盆南北兩側的溫度和鹽度之差；η1和η2分別代表南北兩側的熱力和淡水強迫之差，η3為溫鹽對大氣強迫松弛時間的比值。式（1）和式（2）中所有變量均為無量綱量。在數值離散時采用了二階龍格庫塔方案。時間步長取Δt=0.001。

在積分過程中，各時刻的狀態變量Fi=(Ti,Si)是初始條件(T0,S0)和參數(η1,η2,η3)的函數Fi=Fi(T0,S0;η1,η2,η3)，即狀態變量會隨著初始條件和參數取值的變化而改變。給定η1=3.0，η2=1.02，η3=0.2（將這組參數值分別記為ηb1,ηb2,ηb3），當初始條件取為T0=1.875，S0=1.275時，系統處于平衡態，即此時狀態變量Ti和Si在積分過程中不隨時間變化。為了孤立物理參數變化對狀態變量變化的影響，本文所有試驗的初始條件均取為T0=1.875，S0=1.275。因此，在積分過程中，模型狀態的變化可完全歸因于參數值的變化。

2.2 方法簡介

本研究的試驗設計采用了孿生試驗的假定。首先，假定參數真值為。在真值的設定下，積分模型3 000步，且從第500步開始，每隔200步取一對T和S作為觀測值（To和So）。然后，建立多參數優化系統，將上述觀測同化進系統中。同化系統會根據模型的狀態變量與觀測數據的距離及其梯度等信息，對模型參數進行多次修正，使模型的狀態變量不斷逼近觀測。最后，當模型的狀態變量與觀測的距離達到極小值時，獲得最優參數，或稱最優參數增量，此時需要考察最優參數值能否從最初的（ηb1,ηb2,ηb3）收斂 到 參 數 真 值，或 者 最 優 參 數 增 量（Δη1,Δη2,Δη3）能否從隨機數收斂到參數的增量真值（0.02，-0.03，-0.04）。

在多參數優化系統中，為了衡量模型狀態變量與觀測數據的距離，引入了如下的目標函數：

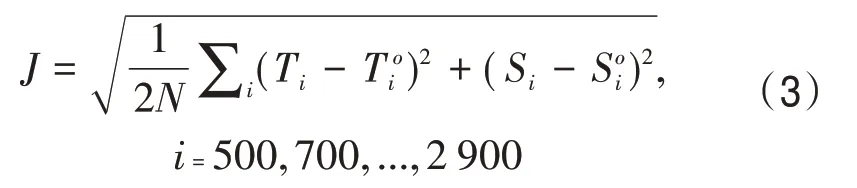
式中：Ti和Si為狀態變量，為參數增量的函數，即Ti=Ti(Δη1,Δη2,Δη3)和和為觀測數據，為常量。時間頻次i由觀測數據確定，從第500個時間步開始，間隔200步取一次，共13個（N=13）。實際上，目標函數即為狀態變量相對于觀測的均方根誤差。

參數估計過程中的關鍵問題在于如何計算梯度，即目標函數對參數增量的梯度(?J/?Δηi,i=1,2,3)。在四維變分同化中，計算梯度需要用到伴隨模式，算法也較為復雜。考慮到盒子模型的參數較少，模型簡單，且積分時間較短，本文采用直接計算梯度的方法。計算目標函數相對于參數增量Δηi的梯度，需分別在ηbi+Δηi和ηbi+Δηi+ε下積分模型，獲得對應的狀態變量F(ηbi+Δηi)和F(ηbi+Δηi+ε)，并計算狀態變量與觀測的距離J(ηbi+Δηi)和J(ηbi+Δηi+ε)。目標函數相對于該參數增量Δηi的梯度即為：

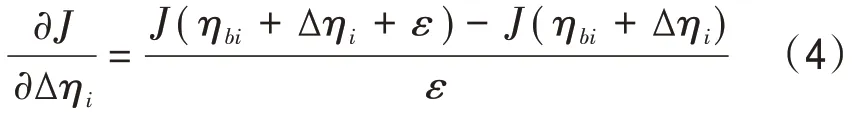
式中：ε為小值，取1.0×10-7。需要說明的是，這種計算方法獲得的梯度精度要高于伴隨（變分）方法的精度，但缺點是每增加一個參數的梯度，需要單獨運行一次模式。

多參數優化系統的優化算法使用了序列二次規劃（Sequential Quadratic Programming，SQP）算法[26-27]，該方法適用于非線性系統的等式和不等式約束規劃問題。理論上講，在參數估計的問題中，不應該設置參數增量（Δη1,Δη2,Δη3）的范圍約束，即參數增量的優化問題是一個無約束的問題。但是考慮到SQP算法的要求，此處將參數增量的范圍設置為[-10，10]，遠遠大于參數真值的變化范圍（0.02，-0.03，-0.04）。如果在參數增量優化過程中達到了給定的范圍邊界，則需將范圍進一步擴大。

綜上，多參數優化系統的計算流程如圖1所示。（1）首先，系統產生隨機數，作為參數增量Δηi的初猜值；（2）將參數增量Δηi疊加到參數基態ηbi上，作為參數值，積分盒子模型，獲得狀態變量的時間序列F(ηbi+Δηi)；（3）基于觀測數據和狀態變量的時間序列，計算目標函數J(ηbi+Δηi)；（4）在參數基態和參數增量(ηbi+Δηi)的基礎上，再疊加一個小擾動ε，并積分盒子模型，獲得狀態變量的時間序列F(ηbi+Δηi+ε)；（5）基于觀測數據和狀態變量的時間序列，計算目標函數J(ηbi+Δηi+ε)；（6）計算目標函數相對于參數增量的梯度?J(ηbi+Δηi)/?Δηi；（7）將 目 標 函 數J(ηbi+Δηi)和 梯 度?J(ηbi+Δηi)/?Δηi輸入優化算法，更新參數增量Δηi；（8）重復過程（2）—（7），直到優化算法達到終止條件；（9）多次重復過程（1）—（8），從目標函數的極小值中找出最小值，并將對應的參數增量作為全局最優的參數增量。在這個流程中，目標函數衡量當前參數設置下模型的狀態變量與觀測之間的距離，梯度提供距離在當前參數增量的一個小鄰域內的導數信息。優化算法基于目標函數與梯度，不斷調整參數值，使狀態變量不斷逼近觀測數據，獲得最優的參數增量。

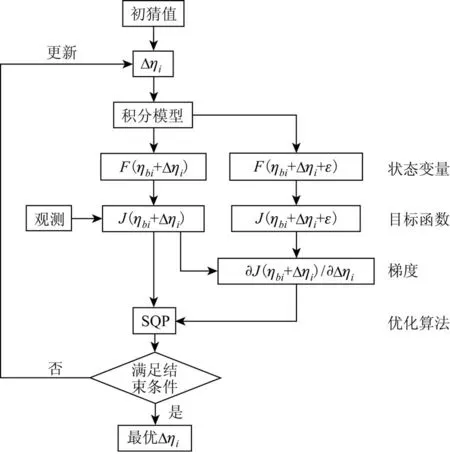
圖1 多參數優化系統的計算流程示意圖

在手動調整模式參數時，人們經常每次只調整1個參數值，在此過程中其他參數值是固定的。調整好1個參數的取值之后，再去調整第2個參數。這種做法是否存在局限性呢？本文設計了兩組試驗，一組同時優化3個參數，另一組分別單獨優化3個參數，用以考察單獨優化參數時，是否可以找到當前參數的真值。在兩組試驗中，梯度的計算方案稍有差別。同時優化3個參數時，相當于在點(ηb1+Δη1,ηb2+Δη2,ηb3+Δη3)的鄰域內計算梯度，如式（5）—（7）所示。單獨優化1個參數時，相當于在點(ηb1+Δη1,ηb2,ηb3)，(ηb1,ηb2+Δη2,ηb3)和(ηb1,ηb2,ηb3+Δη3)的鄰域內分別計算梯度，如式（8）—（10）所示。

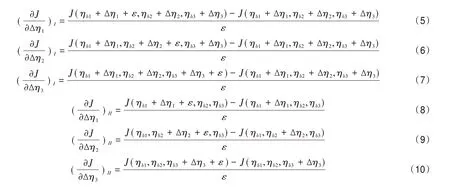
3 結果

3.1 同時優化3個參數

將隨機數作為參數增量的初猜值，基于狀態變量和觀測的距離及其梯度信息，多參數優化系統同時對3個參數增量進行了優化，優化的結果如圖2和表1所示。

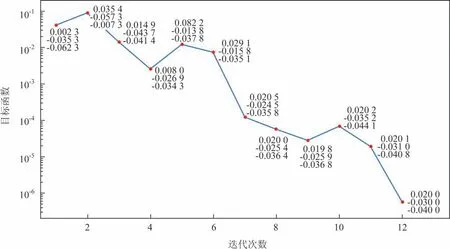
圖2 同時優化3個參數時，目標函數和參數增量的變化（紅色點表示損失函數值，右側的3個數值從上往下依次表示Δη1、Δη2、Δη3的值）

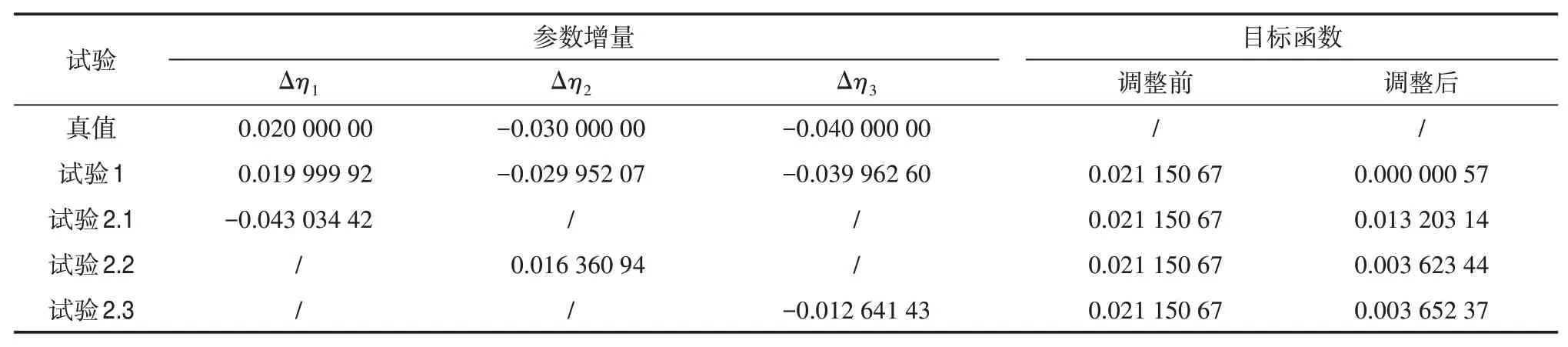
表1 3個參數的增量真值、最優值及其對應的目標函數

優化系統從隨機數開始，經過了12次迭代，收斂到參數增量真值（0.02，-0.03，-0.04）。最優參數增量的誤差量級分別為10-7、10-4和10-4。目標函數（均方根誤差）調整前為2.11×10-2，調整后下降到5.7×10-7。從狀態變量上看（見圖3a—b），調整前參數為基態ηb1,ηb2,ηb3，模型處于平衡態，狀態變量不隨時間變化（藍色線），與觀測數據相差較遠。調整后，狀態變量（紅色線）逼近所有觀測數據。這說明，多參數優化系統可以根據觀測數據和多次模型積分結果，找到參數增量真值。

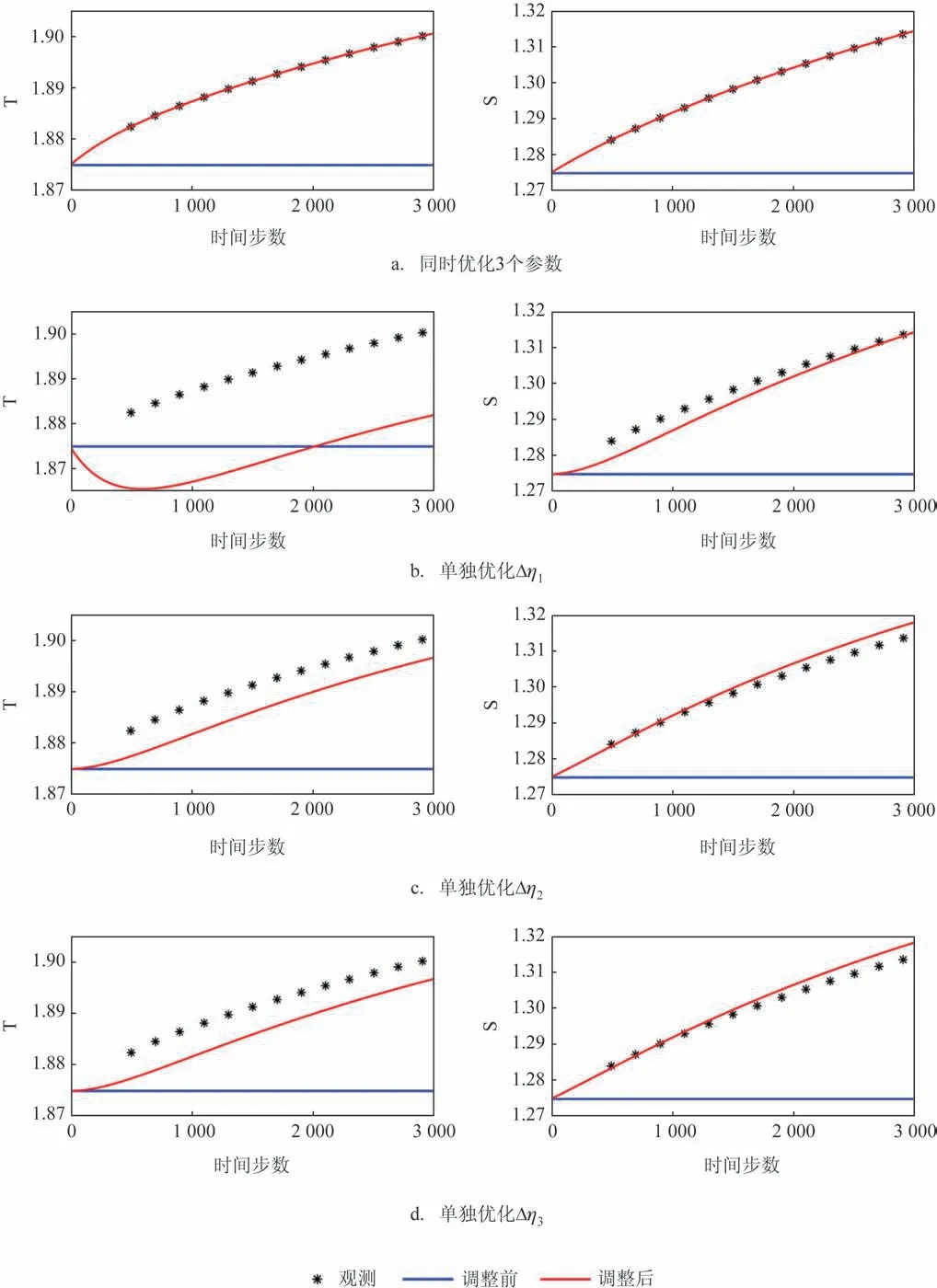
圖3 觀測和模型狀態變量隨積分步數的變化

在每次迭代中，模型需要計算F(ηb1+Δη1,ηb2+Δη2,ηb3+Δη3),F(ηb1+Δη1+ε,ηb2+Δη2,ηb3+Δη3),F(ηb1+Δη1,ηb2+Δη2+ε,ηb3+Δη3)，F(ηb1+Δη1,ηb2+Δη2,ηb3+Δη3+ε)，需積分模型4次，12次迭代共需積分48次。如果給定3個參數增量的搜索半徑[-0.1，0.1]，那么采用遍歷搜索半徑內每個參數增量的方法，為達到上述參數估計的精度，則需要積分模型2×106×2×103×2×103=8×1012次。如此大的運算量，對于簡單的盒子模型都是不可行的，對于復雜的大氣海洋環流模式更是無法實現。這也從另一個角度說明，多參數優化系統在很大程度上降低了模型的積分次數，這在需要較長積分時間的復雜環流模式的參數優化問題中，是尤為有用的。

圖2所示的初猜值符號恰好與增量真值的符號相同，這在一定程度上有助于優化過程的收斂。如果初猜值的符號與真值增量不同，則可能會增加迭代的次數，優化過程可能不收斂于真值增量。然而，在實際情況下，我們無法事先知道真值增量的符號。因此，采用多組隨機初猜值，重復圖1所示的優化過程，是十分必要的。

3.2 單獨優化3個參數

對參數進行手動調整時，人們往往每次只調整1個參數，然后評估該參數對模式模擬的改進程度。將該參數調整到最優之后，再調整下一個參數。從上文的討論中，這相當于在(ηb1+Δη1,ηb2,ηb3)的鄰域內搜索梯度的下降方向和最優參數增量，而不是在(ηb1+Δη1,ηb2+Δη2,ηb3+Δη3)的鄰域內搜索。對于多個參數均存在誤差的情況下，這種方法是否能收斂到3個參數的增量真值？本文設計了另一組試驗，分別單獨優化3個參數增量，考察是否可以得到相應的參數增量真值。

計算結果如表1中試驗2.1—2.3所示。單獨優化Δη1，最優參數增量為-0.043，與增量真值0.02相差較多，目標函數調整前為0.021，調整后下降到0.013。最優參數增量不僅數值上與增量真值相差較多，且符號相反，這說明參數調整的方向是錯誤的。從圖3b中可以發現，調整后S與觀測差別較小，但T與觀測差別較大，甚至較調整之前更大。

單獨優化Δη2時，最優參數增量為0.016，與增量真值-0.03差別較大，且符號相反，目標函數調整前為0.021，調整后下降到0.003 6。最優參數增量與增量真值符號相反，說明Δη2調整的方向也是錯誤的。相對Δη1而言，Δη2優化之后，目標函數下降較多。從圖3c可以發現，優化后的T和S距離觀測相對較近，但效果與同時優化3個參數的情形仍存在較大的差別。

單獨優化Δη3時，最優增量為-0.013，與真值增量相差相對較小，符號相同，目標函數調整前為0.021，調整后下降到0.003 6。相對于Δη1和Δη2，Δη3的最優增量符號與增量真值相同，說明參數調整的方向是正確的。從圖3d可以發現，調整參數后的狀態變量趨近于觀測數據，但效果仍與同時調整3個參數的情形存在一定差異。

以上的試驗結果說明，如果每次只調整1個參數，可能會導致單個參數的調整方向錯誤。在這個錯誤的基礎上，繼續調整第2個參數，必然會導致第2個參數的值出現錯誤。在一組錯誤的最優參數增量設置下，目標函數不可能達到全局最小值。因此，每次只調整一個參數是存在局限的。

4 總結和討論

對于數值模式中少量參數的優化問題，本文建立了一個多參數優化系統，可以對數值模式的多個參數進行同時優化，以減小模式的系統性偏差。該系統設計簡單、易于維護和進一步擴展；系統與數值模式采用文件進行數據交換，因此便于移植到其他數值模式上。

本文將多參數優化系統與一個簡單的盒子模型結合，檢驗了參數優化的效果。首先，基于孿生試驗，預先給定盒子模型的參數真值，并產生觀測數據。然后利用該系統對模型的3個參數同時進行優化。結果顯示，優化算法經過約10次迭代后，系統可以找到預先給定的參數真值。另外，分別單獨優化3個參數時，雖然狀態變量也趨近了觀測，但程度有限；參數增量并不收斂于給定的參數增量真值，甚至會出現最優參數增量與參數增量真值反號的情況。這說明，當人們采用手動方法對模式參數進行逐一、單參數調整時，參數調整的效果具有一定的局限性，而同時調整多個參數可以降低這種局限性。

在實際中，對于復雜的大氣和海洋環流模式，我們無法事先判斷哪些參數是存在誤差的，同時對于大量的參數，限于運算量也無法同時進行調整。從實用的角度講，只要能降低誤差，參數調整就是有意義的，即參數調整無需收斂于真值，而是盡可能大地抵消模式誤差，使模式狀態變量最大程度上趨近于觀測[21]。在這種前提下，同時優化盡可能多的參數，相對于較少的參數，往往可以在更大程度上使狀態變量趨近于觀測。

多參數優化系統具有較好的可移植性。首先，系統采用了直接計算梯度的方式，避免使用復雜的四維變分同化計算方案，尤其是避免了調用伴隨模式。這在很大程度上簡化了系統的復雜性，同時對于目前尚不具備伴隨模式的數值模式（比如多數生態模式和風暴潮增水模式）也可以方便地進行移植。雖然使用直接計算梯度的方式會在一定程度上增加積分模式的次數（每增加1個參數需要多積分模式1次），但是如果同時優化的參數個數少于10個，這種方案的運算量依然是可以接受的。其次，多參數優化系統通過數據文件與模式進行數據交換。系統將模式參數增量值寫入模式的參數文件，模式積分完成后，系統再讀取積分結果，并計算目標函數。在這個流程中，模式積分作為一個獨立的模塊嵌入到系統中，保證了系統可以方便地移植到其他數值模式上。

多參數優化系統是為調整大氣和海洋環流，以及海洋生態等復雜模式中的多個參數設計的，本文是將其應用到簡單模型的一次嘗試和檢驗。在復雜模式中應用該系統需要考慮更多的因素。比如，復雜模式中參數眾多，需要挑選少量重要的參數進行調整，這依賴于一定的參數調整經驗。如果海洋模式中，溫度的垂向廓線誤差較大，那么首先需要調整溫度發展方程中的擴散系數。根據經驗確定了少量重要參數之后，需要對這些參數取值進行擾動，考察這些參數取值的變化是否的確可以引起模式狀態的顯著變化。在復雜模式中，目標函數需要根據關注的問題確定。如果海洋的垂向溫度模擬誤差較大，觀測數據選擇了Argo溫度廓線，那么目標函數可以選擇模式溫度的均方根誤差。此時，參數調整的目標就是降低模式溫度的誤差。另外，復雜模式中不同參數間的取值范圍不同，需要進行歸一化以促進優化算法收斂等。目前，針對南海業務化海洋學預報系統使用的ROMS（Regional Ocean Modeling System）模式，我們已經利用多參數優化系統對其中的5個物理參數同時進行了調整，結果顯示，多個模式變量的模擬得到了顯著的改善，我們將會在另一篇文章中討論這些問題。