水庫大壩工程深基坑支護安全性的有限元分析
楊 瑩
(新疆水利水電勘測設計研究院,烏魯木齊 830000)
0 引 言
基坑工程作為建筑項目中的基礎子工程,在基坑開挖時,需要對周邊土體進行支護,以保證工程的順利開展[1-3]。但對于支護要求較高,同時由于在開挖過程中,施加在支護架上的應力會出現變化,因此對于支護架的位移預測計算較為困難[4-5]。在早期基坑支護安全性的研究中,通常只能使用現有公式對于當前土體、支護材料以及開挖深度等指標進行帶入,大致得出需要的應力。在進行支護時,則往往發現支護架的位移誤差遠大于實際理論誤差值。隨著計算機技術的應用,利用計算機的計算能力可以對影響基坑支護安全的參數進行導入,并進行大量計算,得出相對準確的數據。但結果仍是由固定公式給出,結果準確性仍難以滿足需求[6-8]。現在已開發出有限元分析法,該方法可以實現動態應力分析,大大提高了基坑支護安全性分析結果的準確度。但當前的分析結果缺乏對支護狀態和基坑土體中互斥性的考慮,仍有改善空間[9-11]。
1 水庫大壩工程深基坑支護安全性的有限元分析方法設計
1.1 基坑支護安全性物元描述
傳統有限元分析中,難以將支護狀態下的互斥問題相容化,影響分析結果的可靠性[12-13]。因此,本文選擇采用物元分析法對支護的安全性首先進行物元描述,保證其中存在互斥問題可以共同分析。首先設描述對象為N,支護下的性狀為C,狀態下的量值V,描述中的主要元素為R=(N,C,V)并作為主要元素,并構成物元。而當基坑支護N中,存在若干性狀,則得出n個特征c1、c2、…、cn以及相對應的量值v1、v2、…、vn描述,表示為:
(1)
而通常情況下,支護與基坑之間可以看作存在客觀性矛盾的兩個個體,采用N0代表該支護結構的參照標準,并將性狀ci的值限定為ari≤vn≤bri,而其中的經典域物元矩陣則可以表示為:
(2)
同時需要對上述公式中的數據進行關聯函數計算。假設元素集中的元素定義范圍為X0=[a,b],那么元素模量則為|X0|=|b-a|,而在定義集合中的任一點X距離定義范圍X0=[a,b]的距離如下計算:
(3)
同時其中的關聯函數則可以表示如下:
(4)
式中:p(X,X0)為在點X與范圍X0=[a,b]的差距;p(X,Xp)為點X與范圍Xp=[ap,bp]的差距;X為支護結構的物元量值;X0為經典域物元下的取值幅度;Xp為節域物元的取值幅度。
通過計算以上數值,確定基坑和支護之間的物元描述和誤差值,運用該數值在有限元分析結果的數值中進行誤差修正。
1.2 支護狀態有限元模擬
在分析基坑支護的安全性之前,需要將基坑土體的應力進行模擬分析[14-15]。在基坑處于靜止不動狀態時,圍護機構不存在左右位移,土體本身處在彈性平衡狀態。對于支護中,靜止土體的壓力則為:
P0=(∑γihi+q)K0
(5)
式中:γi為支護點位上的土層重度,kN/m3;q為支護邊坡地面的均布荷載,kPa;hi為支護點位上的土層厚度,m;K0為支護點位上土體的靜止土壓力系數;P0為支護點位上土體的靜止壓力強度,kPa。
同時根據上述內容中對于基坑和支護之間的物元描述,將參數和計算方法引入有限元分析軟件中,利用有限元分析軟件可以模擬支護在開挖狀態下的力學變化。當基坑開挖時,由于土體的自重應力發生改變,土體中的應力分布將會隨著變化,對于支護的安全性也會出現改變。在有限元模擬下,將基坑開挖狀態下的網格圖形態進行呈現,見圖1。
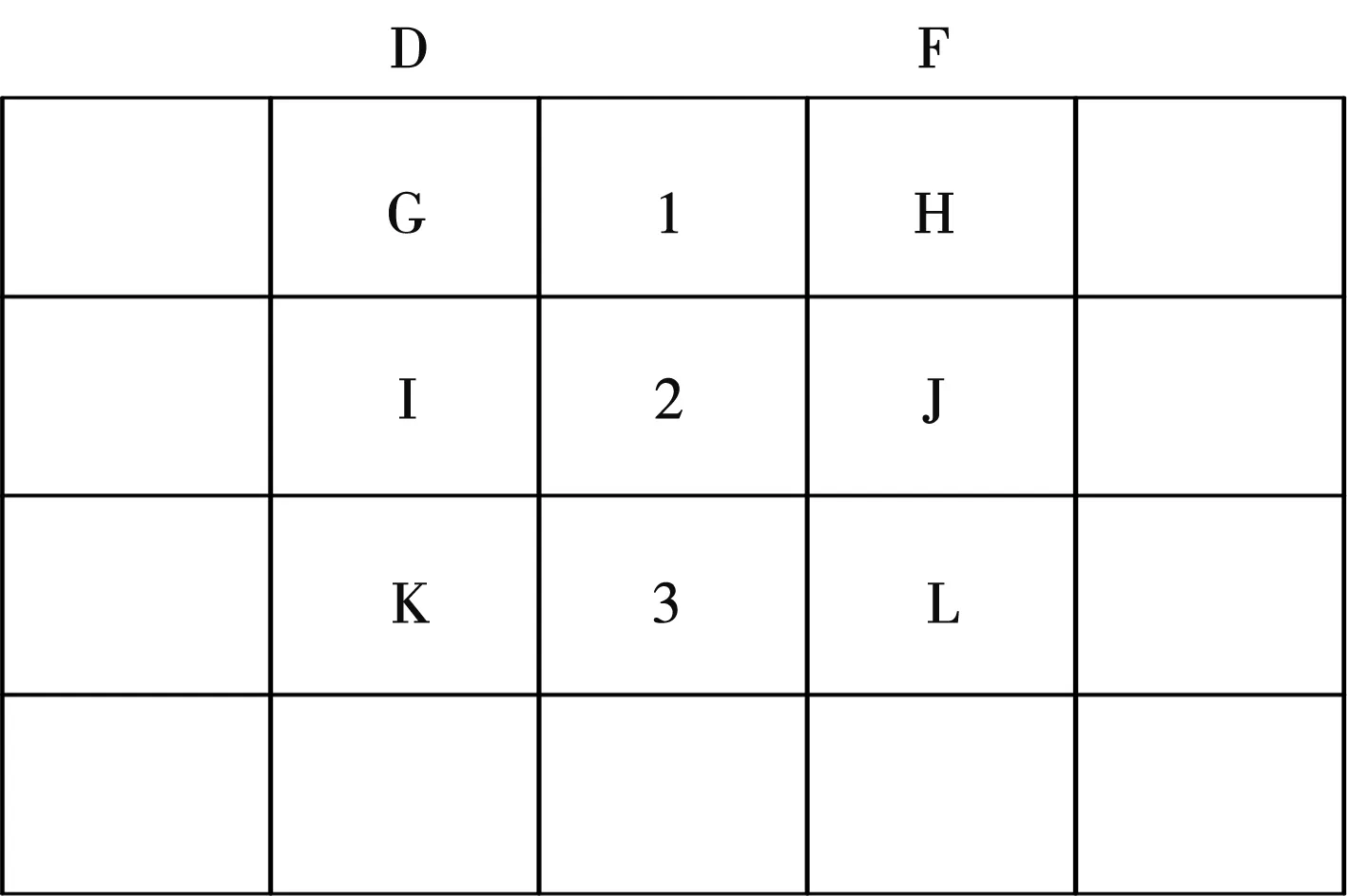
圖1 有限元開挖模擬示意圖
在圖1中,將土體分為多級,實際級數根據工程實際規劃擬定。其中,一級為DFGH,二級為GHIJ,三級則為IJKL。在開挖過程中,開挖土體對于其下部土體作用的等效節點力由自重力得出,即{f}1、{f}2、{f}3。同時根據該地層的地基應力狀態,包括天然應力狀態{σ0}、開挖應變狀態{ε0}以及土體位移狀態{δ0},可以得到對應的內力變形:
(6)
根據上述公式,得出對應開挖面的節點力,獲得有限元的動態力矩模型,以此作為安全性分析的基礎參數值。
1.3 有限元折減安全系數計算
本文在進行有限元折減安全系數中,采用強度參數標準值來進行開挖和計算,參數可由上述計算和有限元分析軟件得出,并得到基坑開挖到坑底的應力狀態并進行迭代計算,以得到安全系數。其中,在進行迭代計算位移增量的公式為:
(7)
式中:δdi為經過第i次迭代的位移子增量;{σi-1}為經過第i次迭代開始的應力穩定值;{F}為支護承載的外部荷載。
在計算過程中,應力點的位置見圖2。
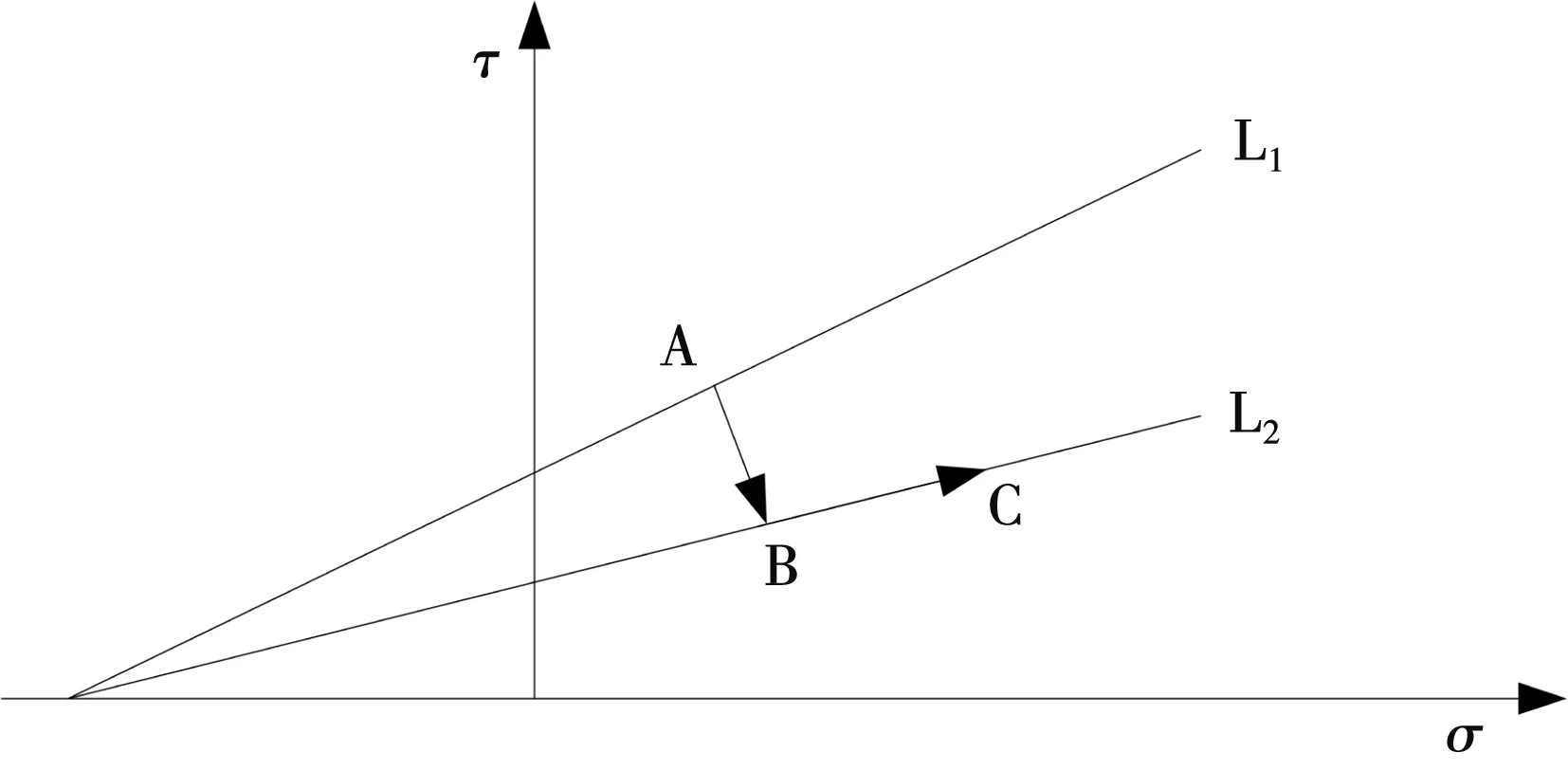
圖2 迭代計算中應力變化圖
在圖1中,支護的屈服面L1的強度在降低后,其參數則變為L2。而在屈服面L1上的點A,在強度降低時則修正到L2上的點B,而后續迭代則會令點B沿L2進行移動,如點C。在迭代過程中,強度參數會出現折減,導致屈服面跟隨迭代過程出現變化,使計算收斂性變差,引出需要調整其中的荷載乘子,本文將其設為m,并作為應力調節過程中的荷載比例,并根據比例來擬定對于強度參數的實際折減量,將處于屈服面L1上的應力進行修正,調整后的強度實際整理值則為:
(8)
其中,下標的A、B、C均為應力對應的點。經過迭代計算后,即可得出不同應力下支護的應力狀況,從而根據擬定的應力要求,得出相應的安全系數。
2 實驗論證分析
為了驗證設計的安全性有限元分析方法的可行性,設計實驗,采用某地水庫大壩工程的基坑支護進行安全性有限元分析,并與文獻[1]、文獻[7]及文獻[9]中的有限元分析法進行對比,判斷有限元分析后的數據準確性,再依據數據準確性得出該方法的安全性和有效性。
2.1 工程介紹
實驗中的水庫大壩控制流域面積為331 km2,庫容為836×104m3。在工程開挖中,需要對被挖表面土體剝離14 721 m3,對深處卵石土體的開挖則需要剝離31 040 m3,對石方的開挖中剝離133 211 m3。在壩體基坑開挖中,最深開挖深度為27 m,在最淺深度為12 m。在該工程中,影響支護結構的土層參數見表1。
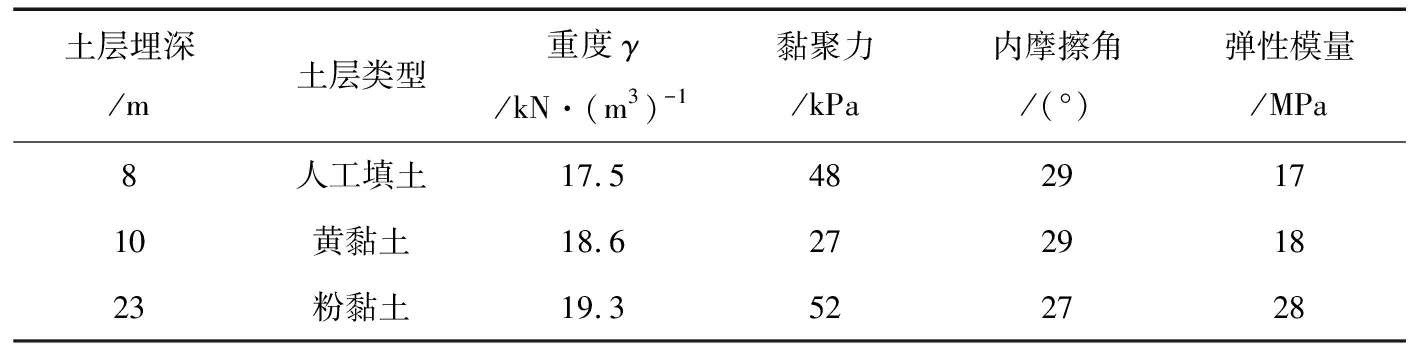
表1 影響支護結構的土層參數
2.2 實驗結果
在對基坑支護的安全性有限元分析中,通常都會提前分析在不同開挖下支護參考點的位移狀況,并以此得出對應的安全性。因此在本文實驗中,主要對照不同有限元分析方法,對基坑開挖過程中準確預先分析出對應的位移量。其中,該工程的支護短邊中點在開挖中的位移見表2。
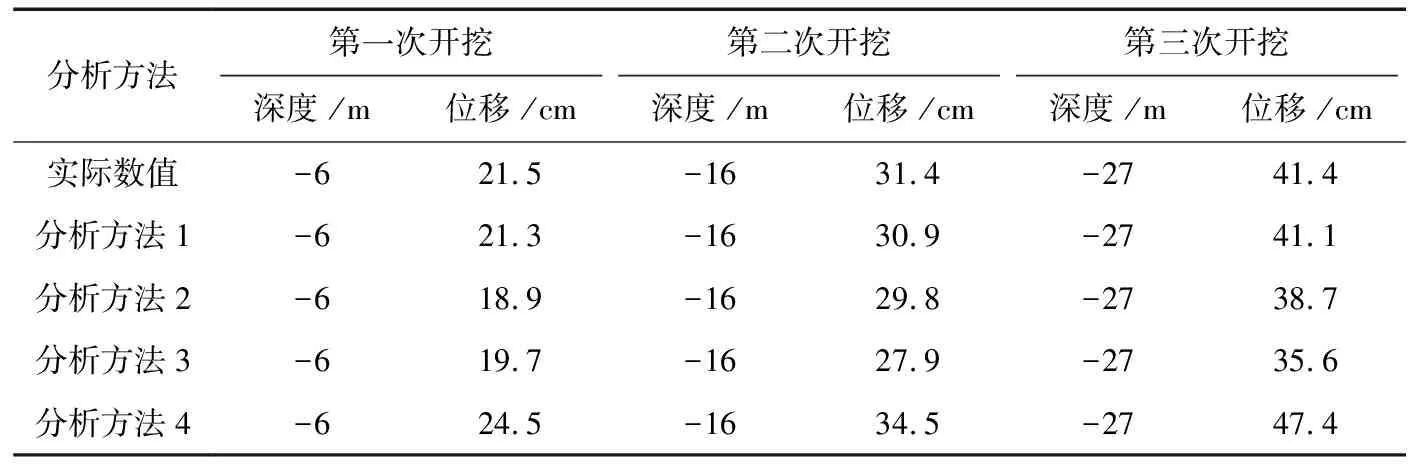
表2 支護短邊中點開挖位移分析
在表2中,分析方法1為本文設計的有限元分析方法,分析方法2為文獻[1]中的分析方法,分析方法3為文獻[7]中的分析方法,分析方法4為文獻[9]中的分析方法。由表2中可以看出,在對不同開挖下的預先分析中,本文設計的有限元分析方法更接近實際數值。
對于支護的長邊中點的位移有限元分析結果見表3。
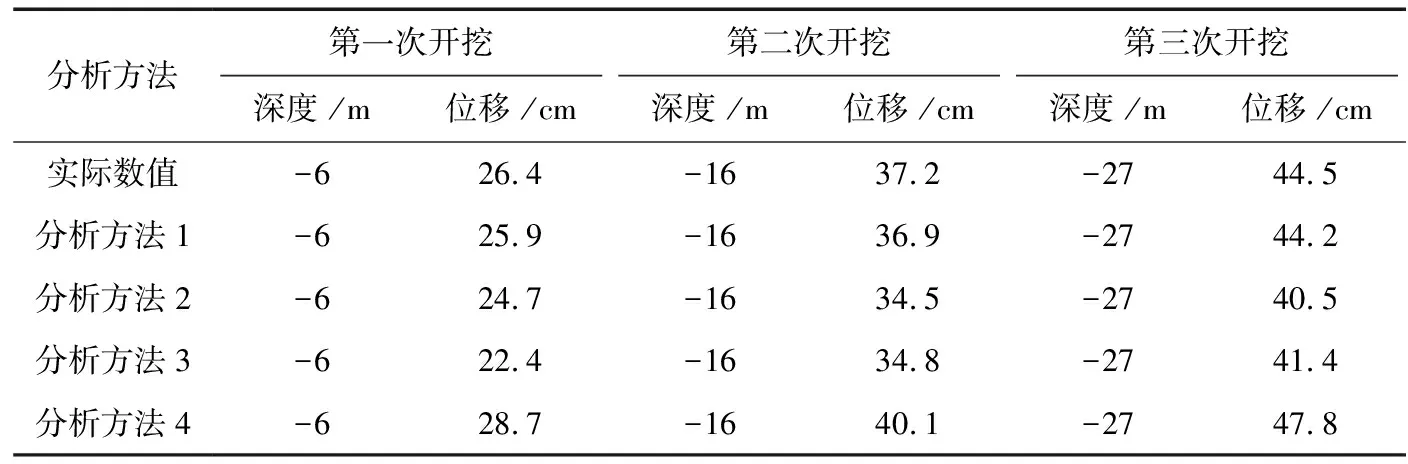
表3 支護長邊中點開挖位移分析
在表3的支護長邊中點的開挖位移分析中,與表2結果類似,本文有限元分析得出的位移值更接近實際數值,說明本文有限元分析結果更接近實際數值。從安全性分析的角度來說,分析中的數據越接近真實數值,說明分析準確度越高,安全性分析時獲得的指標更加準確,由此可證明本文設計的安全性有限元分析方法具有可行性。
3 結 語
本文在有限元分析中,添加了物元描述,以此來降低因基坑土體和支護架之間互斥性對有限元分析結果的影響。實驗結果證明,本文設計的安全性有限元分析方法得出的支護位移結果更接近實際施工結果,證明分析方法的可行性。而在本文分析方法中,將深基坑分為多個網格單元進行分析,導致分析時的運算量過大,對設備的占用較為嚴重。在今后的研究中,將會嘗試采用更簡捷的分析方法來進行分析。

