不對(duì)中－松動(dòng)－碰摩轉(zhuǎn)子系統(tǒng)的動(dòng)力學(xué)特性分析

謝沅博

不對(duì)中－松動(dòng)－碰摩轉(zhuǎn)子系統(tǒng)的動(dòng)力學(xué)特性分析

謝沅博

（蘭州交通大學(xué) 機(jī)電工程學(xué)院，甘肅 蘭州 730070）

考慮聯(lián)軸器不對(duì)中、輸入軸端支座松動(dòng)和轉(zhuǎn)定子間碰摩等耦合故障因素，建立了兩端以滑動(dòng)軸承支撐的非線性剛度雙盤(pán)轉(zhuǎn)子系統(tǒng)動(dòng)力學(xué)模型，運(yùn)用變步長(zhǎng)四階龍格庫(kù)塔法對(duì)該系統(tǒng)進(jìn)行數(shù)值求解，采用分叉圖、相圖、Poincaré截面圖以及最大碰摩力圖主要分析了轉(zhuǎn)速和轉(zhuǎn)盤(pán)偏心量對(duì)系統(tǒng)動(dòng)力學(xué)特性的影響。結(jié)果表明：隨著轉(zhuǎn)速的增大，系統(tǒng)出現(xiàn)了周期運(yùn)動(dòng)、混沌運(yùn)動(dòng)、概周期運(yùn)動(dòng)；轉(zhuǎn)盤(pán)偏心量小范圍的減小會(huì)使系統(tǒng)在低中速區(qū)段運(yùn)行的穩(wěn)定性明顯提高，反之偏心量的增大會(huì)導(dǎo)致系統(tǒng)臨界分叉轉(zhuǎn)速的提前，使原有單周期運(yùn)動(dòng)直接突變?yōu)榛煦邕\(yùn)動(dòng)，轉(zhuǎn)定間的碰摩程度極劇增大。

轉(zhuǎn)子；不對(duì)中；轉(zhuǎn)子偏心；碰摩；分叉

旋轉(zhuǎn)機(jī)械在工業(yè)生產(chǎn)中起著不可動(dòng)搖的地位，而起旋轉(zhuǎn)和支撐作用的轉(zhuǎn)子－軸承系統(tǒng)是其中最關(guān)鍵的部分，但由于非人為因素導(dǎo)致轉(zhuǎn)子－軸承系統(tǒng)產(chǎn)生的故障輕則會(huì)降低旋轉(zhuǎn)機(jī)械的運(yùn)行精度和穩(wěn)定運(yùn)行壽命，重則會(huì)引發(fā)重大機(jī)械損壞和災(zāi)難性后果[1]。

近年來(lái)，國(guó)內(nèi)外學(xué)者對(duì)于轉(zhuǎn)子－軸承系統(tǒng)的研究逐步深入，何振鵬等[2]建立了滑動(dòng)軸承支撐的不含聯(lián)軸器雙盤(pán)轉(zhuǎn)子系統(tǒng)模型以及雙跨含聯(lián)軸器綜合不對(duì)中的轉(zhuǎn)子系統(tǒng)模型，分析了這兩類(lèi)故障轉(zhuǎn)子系統(tǒng)大轉(zhuǎn)速范圍內(nèi)的運(yùn)動(dòng)特征。陳果[3]建立了不平衡碰摩耦合故障轉(zhuǎn)子－軸承系統(tǒng)模型，在考慮VC振動(dòng)的前提下研究了轉(zhuǎn)速、軸承間隙、碰摩剛度和轉(zhuǎn)盤(pán)偏心量對(duì)系統(tǒng)動(dòng)力學(xué)特性的影響。甄滿等[4]采用Newmark-β法對(duì)比研究了含彈性聯(lián)軸器的多跨轉(zhuǎn)子系統(tǒng)在有不對(duì)中故障和無(wú)不對(duì)中故障兩種工況下的動(dòng)力學(xué)特性。Sun W等[5]考慮了在油膜溫度的影響下四自由度的轉(zhuǎn)子－軸承系統(tǒng)所出現(xiàn)的油膜渦動(dòng)和油膜振蕩對(duì)系統(tǒng)穩(wěn)定性的影響。Yang Y等[6]針對(duì)轉(zhuǎn)系－軸承系統(tǒng)考慮碰摩非線性因素，分析了軸徑、涂層、不平衡偏心量對(duì)系統(tǒng)動(dòng)態(tài)特性的影響。劉楊等[7]基于有限元法結(jié)合具體實(shí)驗(yàn)驗(yàn)證研究了考慮含松動(dòng)－碰摩耦合故障轉(zhuǎn)子系統(tǒng)的動(dòng)力學(xué)特性，發(fā)現(xiàn)不同轉(zhuǎn)速下系統(tǒng)頻率和油膜失穩(wěn)現(xiàn)象的變遷規(guī)律。劉杰等[8]考慮非穩(wěn)態(tài)油膜力并結(jié)合實(shí)驗(yàn)對(duì)轉(zhuǎn)軸及轉(zhuǎn)盤(pán)松動(dòng)的轉(zhuǎn)子系統(tǒng)進(jìn)行了動(dòng)力學(xué)特性分析。Liang Ma等[9]對(duì)在齒式聯(lián)軸器不對(duì)中故障下帶擠壓油膜阻尼器的滾動(dòng)軸承轉(zhuǎn)子系統(tǒng)進(jìn)行了動(dòng)力學(xué)分析，基于赫茲接觸和潤(rùn)滑理論研究發(fā)現(xiàn)阻尼器對(duì)系統(tǒng)出現(xiàn)的故障非線性有抑制作用，同時(shí)配合合適的轉(zhuǎn)子剛度以及聯(lián)軸器不對(duì)中程度能增大系統(tǒng)的穩(wěn)定區(qū)間。曾旭焱[10]研究了含碰摩故障的轉(zhuǎn)子－滾動(dòng)軸承系統(tǒng)的動(dòng)力學(xué)特性，并用簡(jiǎn)單胞映射方法發(fā)現(xiàn)系統(tǒng)存在周期一和周期三吸引子共存現(xiàn)象。

綜上所述目前對(duì)于考慮聯(lián)軸器不對(duì)中、支座松動(dòng)以及碰摩耦合故障的雙盤(pán)非線性剛度轉(zhuǎn)子的研究還不多，有鑒于此，本文在馬輝等[11]提出的新松動(dòng)模型基礎(chǔ)上建立了雙盤(pán)滑動(dòng)軸承支撐下含聯(lián)軸器不對(duì)中，一端支座松動(dòng)和碰摩耦合故障轉(zhuǎn)子系統(tǒng)，采用龍格庫(kù)塔數(shù)值積分法對(duì)系統(tǒng)進(jìn)行數(shù)值仿真，分析了不同轉(zhuǎn)速及不同轉(zhuǎn)速下偏心量對(duì)系統(tǒng)動(dòng)力學(xué)行為的影響，可以為分析實(shí)際生產(chǎn)中的轉(zhuǎn)子－軸承系統(tǒng)正常運(yùn)行以及為預(yù)防故障的發(fā)展提供一定的指導(dǎo)和理論參考。

1 系統(tǒng)動(dòng)力學(xué)模型

圖1所示為不對(duì)中－松動(dòng)－碰摩轉(zhuǎn)子系統(tǒng)，雙盤(pán)轉(zhuǎn)子兩端以相同的滑動(dòng)軸承支撐。

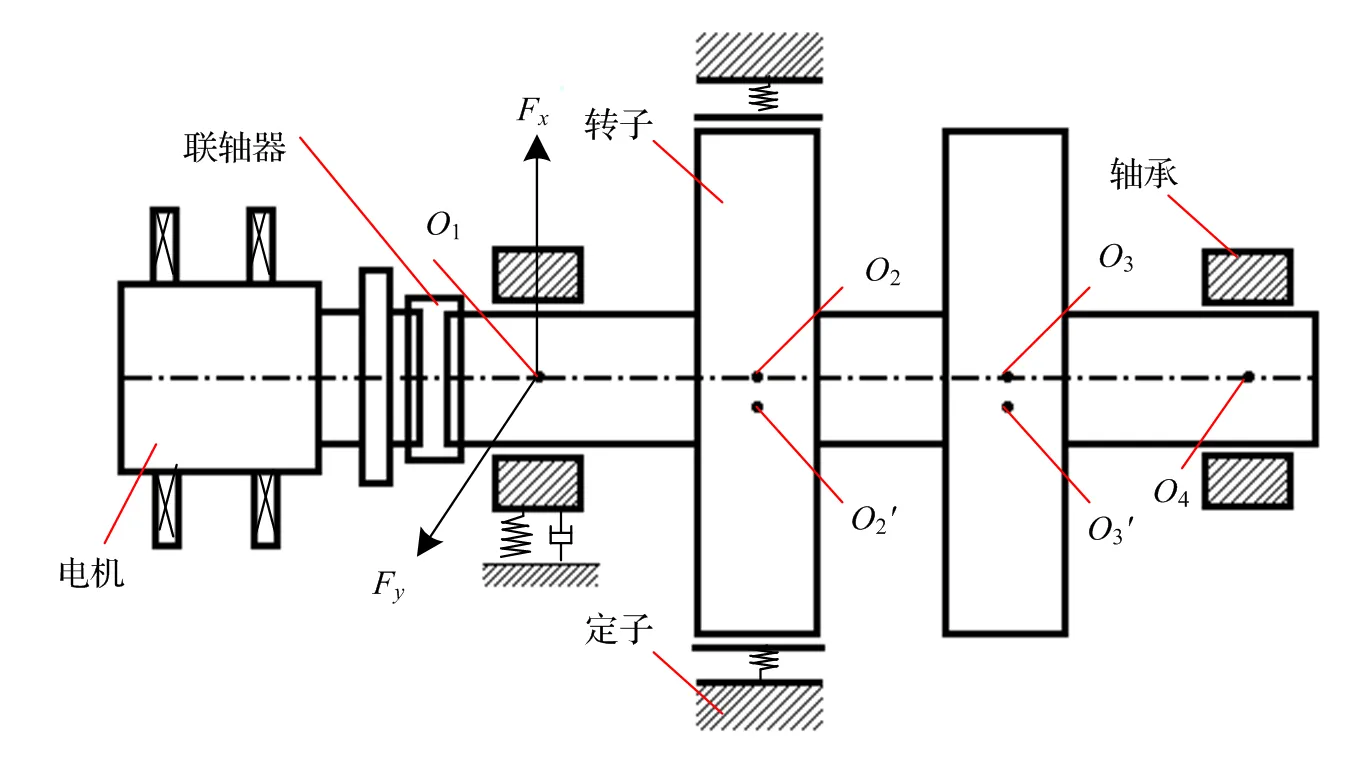
O1和O4分別為左邊和右邊軸承軸瓦的幾何中心；O2和O3分別為左邊和右邊轉(zhuǎn)盤(pán)的幾何中心；O2' 和O3'分別為左邊和右邊轉(zhuǎn)盤(pán)的質(zhì)心；Fi(i＝x, y)為軸承作用在軸上的油膜力。

1.1 聯(lián)軸器不對(duì)中模型

電機(jī)輸出軸靠聯(lián)軸器與轉(zhuǎn)子系統(tǒng)輸入軸相連來(lái)傳遞扭矩。聯(lián)軸器不對(duì)中故障主要是聯(lián)軸器角度不對(duì)中、聯(lián)軸器平行不對(duì)中和前兩者均存在的綜合不對(duì)中，如圖2所示。

當(dāng)電機(jī)主動(dòng)軸通過(guò)聯(lián)軸器齒套帶動(dòng)轉(zhuǎn)子從動(dòng)軸運(yùn)動(dòng)時(shí)，中間齒套質(zhì)心做圓周運(yùn)動(dòng)，綜合不對(duì)中量由平行不對(duì)中和角度不對(duì)中表示為：

式中：Δ為綜合不對(duì)中量，mm；為平行不對(duì)中量，rad；Δ聯(lián)軸器間距，mm；為角度不對(duì)中量，rad。

圖2 不對(duì)中模型

聯(lián)軸器殼體和齒套質(zhì)心的運(yùn)動(dòng)軌跡可表示為：

根據(jù)式（2）求其對(duì)時(shí)間的二階導(dǎo)數(shù)得到加速度，則不對(duì)中的影響等效于在轉(zhuǎn)子左端施加了一個(gè)不對(duì)中激振外力，該力表示為：

1.2 支座松動(dòng)等效剛度模型

轉(zhuǎn)子系統(tǒng)在正常運(yùn)轉(zhuǎn)過(guò)程中可能會(huì)因?yàn)楹芏嘣蛑率怪ё蓜?dòng)產(chǎn)生間隙，比如固定支座的螺栓未擰緊、由于制造精度誤差使支座與基礎(chǔ)的切合面非平行切合等。而在考慮支座松動(dòng)對(duì)轉(zhuǎn)子系統(tǒng)的影響時(shí)假設(shè)松動(dòng)間隙相比轉(zhuǎn)子在豎直方向上的位移小很多，并且不計(jì)松動(dòng)間隙引起的偏心問(wèn)題和轉(zhuǎn)子剛度的變化，同時(shí)這里僅考慮鉛錘方向的松動(dòng)。分段線性的具體表達(dá)式為：

式中：為支座松動(dòng)間隙，mm；c為不同位移條件下基礎(chǔ)對(duì)支座的等效阻尼，N·s·m-1；k為不同位移條件下基礎(chǔ)對(duì)支座的剛度，N·s·m-1；＝1,2。

1.3 碰摩力模型

當(dāng)轉(zhuǎn)子隨著轉(zhuǎn)速的提高徑向振動(dòng)位移大于轉(zhuǎn)盤(pán)與定子之間的間隙時(shí)發(fā)生碰摩，如圖3所示。

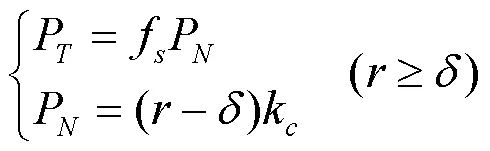
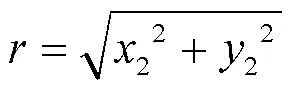
將該碰摩力分解到如圖3所示軸方向、軸方向可以得到碰摩力在軸方向、軸方向上的分量和為：

1.4 短圓瓦軸承油膜力模型

設(shè)f和f是該軸承的無(wú)量綱油膜力，采用收斂性比較好的Capone短軸承油膜力模型，油膜力滿足雷諾方程，計(jì)算公式為[12]：

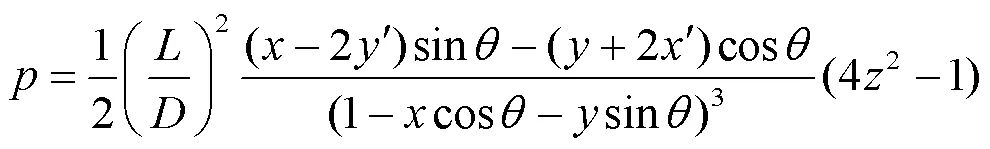
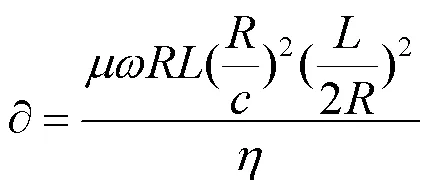
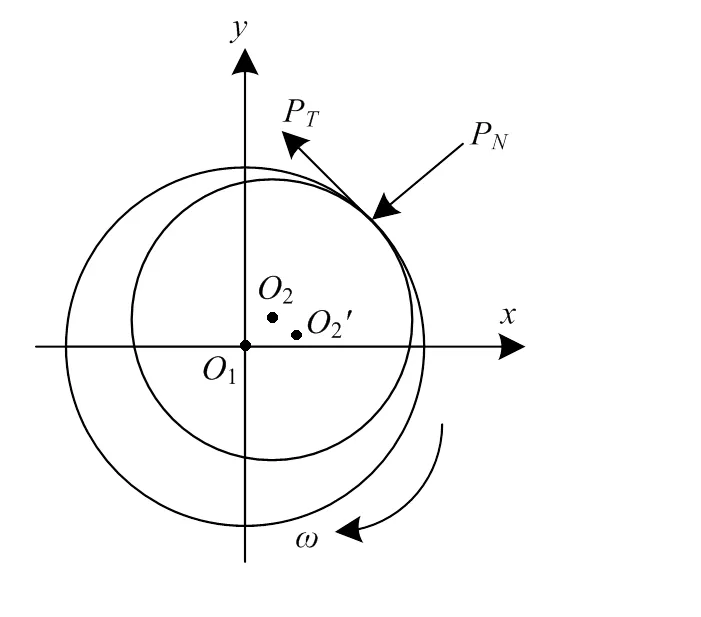
PT為在接觸點(diǎn)處的切向載荷，N；PN為在接觸點(diǎn)處的法向載荷，N。

則滑動(dòng)軸承處的油膜力分量f(,,,)和f(,,,)可以表示為：

1.5 系統(tǒng)運(yùn)動(dòng)微分方程

轉(zhuǎn)子支撐軸因其應(yīng)變和應(yīng)力的關(guān)系是非線性函數(shù)關(guān)系，所以一般來(lái)說(shuō)剛度也是非線性的。為了更加準(zhǔn)確描述實(shí)際生產(chǎn)中的非線性剛度轉(zhuǎn)子，這里引入由Cveticanin[13]提出的線性項(xiàng)與立方項(xiàng)之和關(guān)系導(dǎo)出的轉(zhuǎn)軸非線性彈性力為：

式中：為彈性軸線性剛度，N·m-1；k為彈性軸立方非線性彎曲剛度，N·m-1。

如圖1所示，設(shè)系統(tǒng)在左端軸承1處、左轉(zhuǎn)盤(pán)2處、右轉(zhuǎn)盤(pán)3處、右端軸承4處的軸心徑向位移分別為（1,1）、（2,2）、（3,3）、（4,4），則系統(tǒng)的微分方程為式（11）。式中：為重力加速度，m/s2；m為左端松動(dòng)支座質(zhì)量，kg。

為了方便計(jì)算，取如下無(wú)量綱變換[2]：

2 仿真計(jì)算結(jié)果及其分析

采用變步長(zhǎng)四階Runge-Kutta法對(duì)系統(tǒng)進(jìn)行數(shù)值仿真積分，以表1中的參數(shù)作為基準(zhǔn)參數(shù)來(lái)分析系統(tǒng)的振動(dòng)響應(yīng)和分叉特性。

2.1 轉(zhuǎn)速的影響

表1 系統(tǒng)基準(zhǔn)參數(shù)

注：1代表左軸承；2代表左轉(zhuǎn)盤(pán)；3代表右轉(zhuǎn)盤(pán)；4代表右軸承。

圖4 基準(zhǔn)參數(shù)下系統(tǒng)分叉圖和最大碰摩力圖

2.2 偏心量的影響

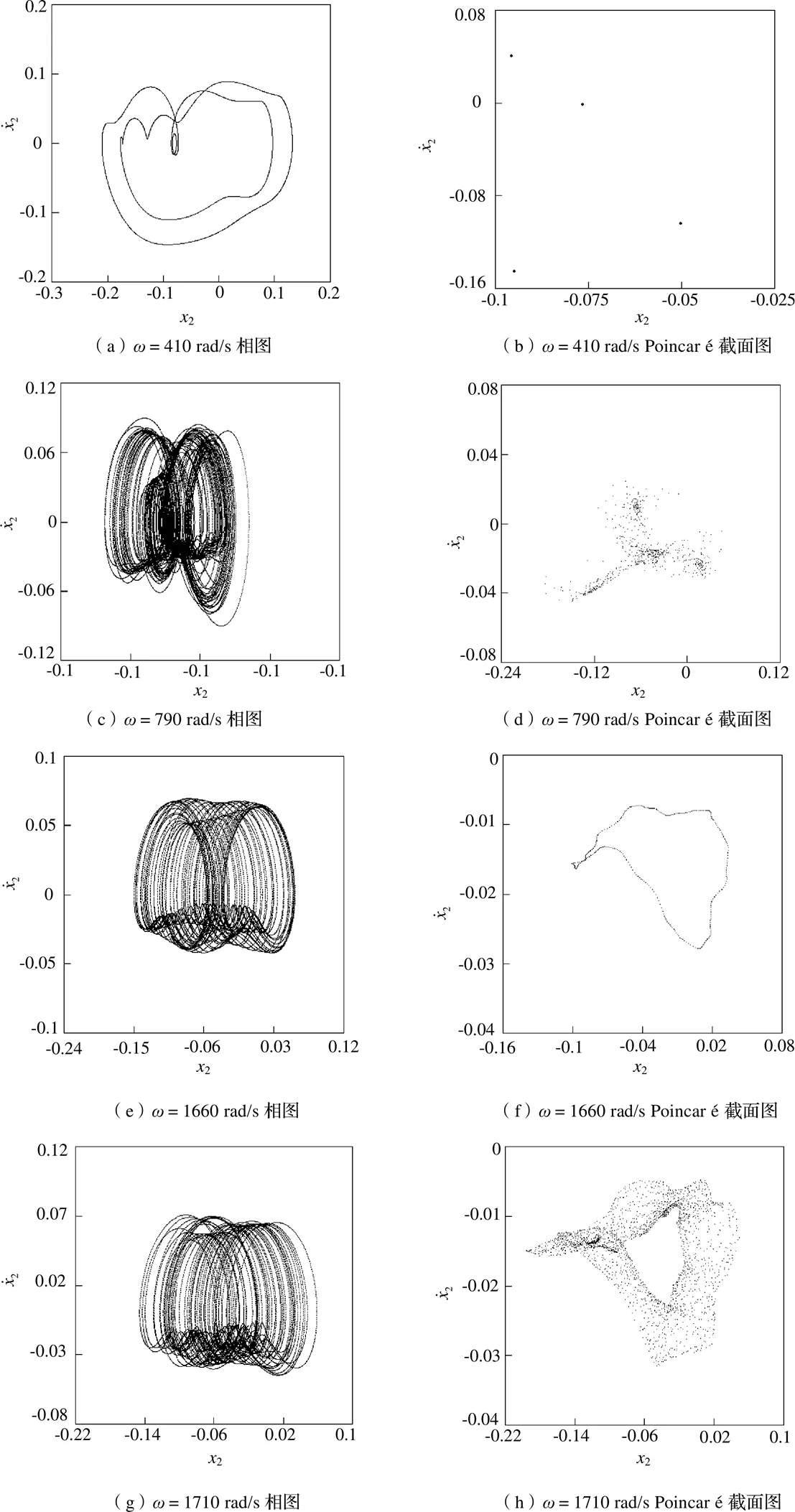
圖5 各個(gè)轉(zhuǎn)速對(duì)應(yīng)的相圖和Poincaré截面圖

圖6 偏心量對(duì)系統(tǒng)動(dòng)力學(xué)響應(yīng)的影響

圖7 不同偏心量下的最大碰摩力圖

3 結(jié)論

本文建立了含不對(duì)中－松動(dòng)－碰摩耦合的故障轉(zhuǎn)子系統(tǒng)，主要分析了系統(tǒng)轉(zhuǎn)速和轉(zhuǎn)盤(pán)偏心量1這兩個(gè)重要的參數(shù)對(duì)系統(tǒng)動(dòng)力學(xué)特性以及分叉的影響。

（1）基準(zhǔn)參數(shù)下隨著轉(zhuǎn)速的變化系統(tǒng)出現(xiàn)了周期運(yùn)動(dòng)、混沌運(yùn)動(dòng)、概周期運(yùn)動(dòng)以及多周期與混沌交替的復(fù)雜運(yùn)動(dòng)，在多故障耦合因素的影響下系統(tǒng)在不同臨界轉(zhuǎn)速附近會(huì)以不同的分叉方式進(jìn)入混沌運(yùn)動(dòng)。

（2）轉(zhuǎn)盤(pán)偏心量1小范圍的減小會(huì)使系統(tǒng)在低中速區(qū)段的碰摩程度減輕，在400 rad/s附近的混沌運(yùn)動(dòng)和520 rad/s開(kāi)始的多周期與混沌交替運(yùn)動(dòng)被周期運(yùn)動(dòng)所替代，系統(tǒng)在低中速區(qū)段的穩(wěn)定性明顯提高。反之偏心量1的增大會(huì)使系統(tǒng)的臨界分叉轉(zhuǎn)速提前，500rad/s附近混沌響應(yīng)區(qū)段變寬的同時(shí)原有860 rad/s處的單周期區(qū)域直接突變?yōu)榛煦邕\(yùn)動(dòng)，對(duì)比之下轉(zhuǎn)定間的無(wú)量綱碰摩力驟增，因此轉(zhuǎn)定間的碰摩也變得非常嚴(yán)重。

[1]王延博. 大型汽輪發(fā)電機(jī)組軸系不對(duì)中振動(dòng)的研究[J]. 動(dòng)力工程，2004（6）：768-774，784.

[2]何振鵬，徐唐進(jìn)，劉佳航，等. 具有不對(duì)中故障的轉(zhuǎn)子滑動(dòng)軸承系統(tǒng)動(dòng)力學(xué)特性研究[J]. 潤(rùn)滑與密封，2018，43（8）：36-45.

[3]陳果. 具有不平衡－碰摩耦合故障的轉(zhuǎn)子－滾動(dòng)軸承系統(tǒng)非線性動(dòng)力學(xué)研究[J]. 振動(dòng)與沖擊，2008（4）：43-48，167-168.

[4]甄滿，田擁勝，孫濤，等. 具有不對(duì)中故障的雙跨轉(zhuǎn)子系統(tǒng)非線性動(dòng)力學(xué)特性[J]. 機(jī)械工程學(xué)報(bào)，2020，56（16）：109-117.

[5]Sun W, Yan Z, Tan T, et al. Nonlinear characterization of the rotor-bearing system with the oil-film and unbalance forces considering the effect of the oil-film temperature[J]. Nonlinear Dynamics，2018，92（3）：1119-1145.

[6]Yang Y , Cao D , Xu Y . Rubbing analysis of a nonlinear rotor system with surface coatings[J]. International Journal of Non-Linear Mechanics, 2016，84：105-115.

[7]劉楊，李炎臻，太興宇. 轉(zhuǎn)子－滑動(dòng)軸承系統(tǒng)松動(dòng)－碰摩耦合故障分析[J]. 振動(dòng)工程學(xué)報(bào)，2016，29（3）：549-554.

[8]劉杰，李志農(nóng)，盧文秀. 非穩(wěn)態(tài)油膜力對(duì)轉(zhuǎn)子系統(tǒng)盤(pán)軸松動(dòng)故障的影響研究[J]. 振動(dòng)與沖擊，2019，38（17）：268-275.

[9]Ma L，Zhang J，Lin J，et al. Dynamic characteristics analysis of a misaligned rotor-bearing system with squeeze film dampers[J]. Journal of Zhejiang University Science，2016，17（8）：614-631.

[10]曾旭焱. 含碰摩故障的雙盤(pán)轉(zhuǎn)子－滾動(dòng)軸承系統(tǒng)動(dòng)力學(xué)特性分析[J]. 現(xiàn)代制造工程，2020（8）：141-146.

[11]馬輝，孫偉，王學(xué)軍，等. 轉(zhuǎn)子系統(tǒng)松動(dòng)故障特征分析[J]. 東北大學(xué)學(xué)報(bào)（自然科版），2009，30（3）：400-404.

[12]劉長(zhǎng)利，夏春明，鄭建榮，等. 碰摩和油膜耦合故障轉(zhuǎn)子系統(tǒng)周期運(yùn)動(dòng)分岔分析[J]. 振動(dòng)與沖擊，2008（5）：85-88，176.

[13]Cveticanin L. A necessary condition for chaos in rotor systems[J]. Mechanism and Machine Theory，1997，32（3）：411-416.

Dynamic Analysis of Rotor System with Misalignment, Loose and Rub-Impact

XIE Yuanbo

( School of Mechanical Engineering, Lanzhou Jiaotong University,Lanzhou 730070, China)

Aiming at the coupling fault factors such as coupling misalignment, loosening of the input shaft end support and the rubbing between the rotor and stator, a dynamic model of a dual-disk rotor system with nonlinear stiffness supported by sliding bearings at both ends is established. The numerical analysis of the system is conducted by using variable step fourth-order Runge-Kutta method, and the bifurcation diagram, phase diagram, Poincaré sectional diagram and maximum rubbing force diagram are used to analyze the influence of the rotation speed and the turntable eccentricity on the dynamic characteristics of the system. The results show that the increase of the speed leads to the periodic motion, chaotic motion, pseudo-periodic motion of the system; the reduction of the turntable eccentricity in a small range significantly improves the stability of the system in the low and medium speed range. Conversely, the increase of the eccentricity leads to the advancement of the critical bifurcation speed of the system, which mutates the previous single-period motion directly into chaotic motion, and the degree of the rubbing between the rotor and stator is greatly increased.

rotor；misalignment；rotor eccentricity；rubbing-impact；bifurcation

TH113.1

A

10.3969/j.issn.1006-0316.2021.08.006

1006-0316 (2021) 08-0037-09

2021-01-07

謝沅博（1995－），男，四川南充人，碩士研究生，主要研究方向?yàn)榉蔷€性動(dòng)力學(xué)，E-mail：1726845017@qq.com。