“田忌賽馬”中的社會契約與創新激勵
陸文玥 劉志闊 段劍輝


摘要:“田忌賽馬”反映了在保持社會契約的權威性和激勵人力資本創新方面的策略觀。基于現代契約經濟學理論,從“立約-違約”雙向契約敘事視角出發,文章通過構建博弈模型,提出序貫博弈下齊王的“相馬”策略,探究其中蘊含的人力資本產權和創新激勵機制。在對剩余控制權和剩余索取權的爭奪中,馬匹的能力和序貫博弈為齊王提供了控制權優勢,同時通過交換收益權,激發“創造性破壞”,在維護社會契約權威性的同時激勵創新。
關鍵詞:田忌賽馬;契約經濟學;人力資本;創新激勵
一、文獻綜述
對“田忌賽馬”問題,國內學者分別從策略性、是否存在違規、選拔機制、賽馬歷史等方面進行了研究。陜聲祥(2017)認為,出馬順序是賽前共同約定的重要規則,田忌通過改變這一規則而獲勝,反映出他重功利、輕規則,因此勝之不武。柯政(2016)認為,“賽馬”助長了考生從功利而非興趣或特長出發選擇科目的傾向,因此這種激勵機制不利于選賢用能。張建發(2017)認為,田忌并未突破規則,而是通過靈活變通的方式提高了比賽的績效。尹向飛和陳柳欽(2006)建立了模型,驗證了田忌的出馬順序是最優策略,提出存在權能謀事的最優策略定理。崔立根(2014)認為,賽馬實為一種政治活動,旨在通過競爭與溝通選拔人才,而非選拔良馬。
本文將齊王與諸公子(整體)之間的賽制約定視為一種權威性的社會契約(一級契約),將齊王-田忌-其他諸公子的非合作博弈視為一種競爭性契約(二級契約)。由于契約是不完全的,賽馬者之間必然存在著對剩余控制權和剩余索取權的爭奪。就機制設計而言,是否存在著一種既保證參與約束又提供激勵相容的機制?換言之,齊王在確保社會契約條件下的控制權基礎上,如何通過收益權的轉讓激勵孫臏這樣的人才脫穎而出?
假設1:一級契約具有權威性。
假設2:一級契約下的承諾未必可信。
假設3:違約須具有程序正義性。
假設4:二級契約下存在信息不對稱。
假設5:二級契約下存在集體行動邏輯。
假設6:各小國間存在競爭性的人才市場。
二、一級契約與序貫博弈
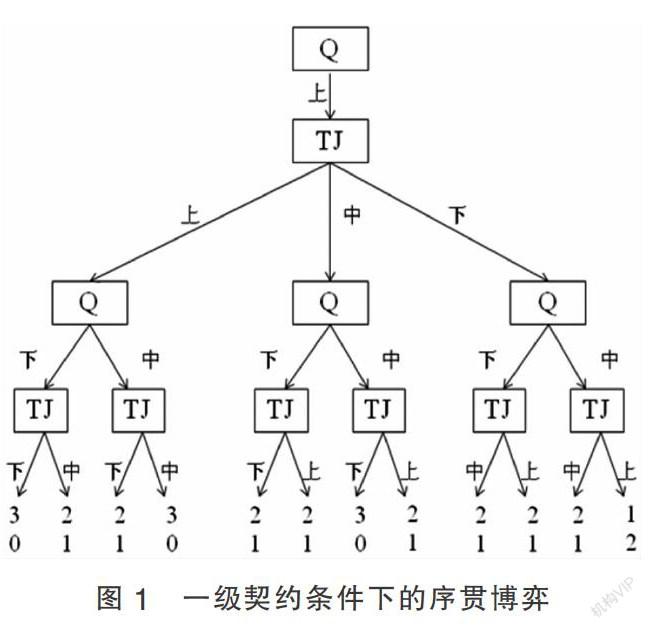
假設將“諸公子”視為一個整體,該比賽是“諸公子”T和齊王Q之間的一場2×2零和博弈。但在操作層面,賽馬是按“下-上”、“上-中”、“中-下”的回合分三輪進行的,因此實際上是一種序貫博弈。齊王在第二輪具有權變的權利,即根據田忌在第一輪的策略適時調整戰術的權利。如圖1所示,齊王和田忌分別用Q和TJ表示,每輪馬匹的品級由上、中、下表示,按照三局兩勝的慣例,在第二輪結束時即可確定二人的得分,設每輪勝出得1分,每輪失敗得0分,支付如下。
由圖1可知,由于齊王擁有事后權變機會,因此田忌以“下-上-中”獲勝的概率只有,全盤皆輸的概率為,獲勝一輪的概率為,而齊王獲勝的概率則達。可見,齊王在比賽中具有絕對的控制權優勢,因此一級契約的存續是有保障的。無論是從齊王馬匹的能力還是從序貫博弈所帶來的主動權而言,齊王都沒有必要主動違約。此外,齊王的承諾之所以可信,還與諸公子內部的集體博弈困境有關,即二級契約博弈。
三、二級契約與集體行動博弈
假設存在兩種契約類型,既定契約a和備選契約集B,二者同時競爭,bi∈B,nb≥2。在不完全契約條件下,a有被違約的可能,即a有被bi替代的可能。假設替代策略為S1或s1,不替代策略為S2或s2。如果bi優于a,則有替代的可能,概率為0≤pi≤1,p1+p2+…+pi=1,i∈n為。然而,由于存在違約和再談判等導致的交易費用,因此可視為既有契約a對任何替代者的潛在懲罰,設為支付-α(α>0),而如果維持a,則不存在這一支付,即α=0。于是,bi面臨兩種效用因素,即替代a和遭受a的懲罰。在一場“贏者全得”的博弈中,勝出者得到支付w(w>0),其他得到支付0。同時,bi會預期到,即使替代了a,也將面臨契約集B中其他契約替代的潛在可能性。假設在a契約仍為所有當事人所遵守的情況下,B中各契約均為備選契約,彼此之間存在競爭但不存在懲罰,懲罰只來自既有契約a對bi潛在替代的反應。換言之,即使bi成功替代a(同時獲得支付-α),也并不能確保自身不受B集合中其他成員發起替代,故其預期支付為EVi=-α×(1-pi)+(w-α)×pi=wpi-α。現僅考慮B集合中任意兩個契約b1和b2之間的博弈(見圖2)。
經推導可知①,b1和b2分別選擇發起或不發起替代行為作為其占優策略的條件如表1所示。
此外,當w>α且wpi<α時,存在兩個納什均衡,即(s2,S1)和(s1,S2),b1和b2均無占優策略。這是一個“貢獻博弈”,即盡管各方都希望對方承擔貢獻公共品的成本,但并不能排除自己做此貢獻并獨自承擔成本(或交易費用)的可能。然而,本例中,不僅面對公共品成本問題,還面對收益激勵問題,因此需要進一步分析。由于二者在此條件下均無占優策略,因此考慮契約數量的影響。
假設這些競爭性契約個體在體現整體特征方面是均質的,因此將它們各自發起替代的行為視為具有相同的概率值γ。如此,假設bi發起替代行為的概率為γ,不發起的概率為1-γ。除bi以外,其他所有n-1個參與者都發起替代行為的概率為γn-1,而不發起的概率為1-γn-1。以P1為例。在均衡條件下,它對兩種選擇是無差異的,因此設其純策略的預期支付相等,即
EV1=γn-1×(wp1-α)+(1-γn-1)(w-α)=0
s.t. w>α,wp1<α
經計算得
γ=[]
對wp1<α兩邊乘以-1,再加上w,得w-α

