聯(lián)合仿真模型中代數環(huán)求解問題

王慧雙 李琳琳

摘? 要：FMI聯(lián)合仿真標準，用來作為不同學科仿真工具的數據交互接口，將這些系統(tǒng)中由不同仿真工具建立的仿真過程以數據形式連接起來，形成統(tǒng)一的仿真耦合系統(tǒng)。反饋回路是許多復雜仿真系統(tǒng)在運用計算機技術進行系統(tǒng)仿真模擬時，由于計算機是按照一定的時序進行計算的，所以存在反饋回路的仿真系統(tǒng)就會產生代數環(huán)結構。該文通過引入解非線性方程組的方法解決FMI聯(lián)合仿真系統(tǒng)中的代數環(huán)問題。

關鍵詞：FMI聯(lián)合仿真技術? 代數環(huán)? tarjan算法? 牛頓迭代法

中圖分類號：O151? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A文章編號：1672-3791（2021）05（a）-0038-03

Abstract： FMI joint simulation standard is used as the data interaction interface of simulation tools of different disciplines， which connects the simulation processes established by different simulation tools in these systems in the form of data to form a unified simulation coupling system. Feedback loop is a complex simulation system. When computer technology is used to simulate the system， because the computer calculates according to a certain time sequence， the simulation system with feedback loop will produce algebraic loop structure. In this paper， the algebraic loop problem in FMI joint simulation system is solved by introducing the method of solving nonlinear equations.

Key Words： FMI joint simulation technology; Algebraic rings; Tarjan algorithm; Newton's method

利用仿真模擬實際系統(tǒng)中的運行情況，進而實現系統(tǒng)的優(yōu)化。考慮到各學科的耦合作用和影響，為了實現對研究對象在實際情況中更為精確、高效，多學科聯(lián)合仿真的概念應運而生[1]。FMI聯(lián)合仿真標準為多學科聯(lián)合仿真模型提供了數據交互接口和通信協(xié)議。聯(lián)合仿真系統(tǒng)中的代數環(huán)問題，影響著聯(lián)合仿真的仿真精度與速度，該文應用DFS理論對各聯(lián)合仿真模型之間的控制信息進行檢索，并提出了一種基于解非線性方程的方法對聯(lián)合仿真模型中的代數環(huán)結構進行求解。

1? 基于tarjan算法的代數環(huán)檢測

1.1 圖論基礎知識

1.1.1 強連通圖

由有向邊構成的圖成為有向圖，并且在有向圖中的任意一頂點都有到達其他頂點的路徑，則稱為強連通圖[2]。

1.1.2 強連通分量

在非強連通圖中的連通部分。其中，獨立的頂點也稱為一個強連通分量。

1.2 Tarjan算法

Tarjan算法是基于對圖深度優(yōu)先搜索的算法，用于求解圖的連通性問題，每個強連通分量為搜索樹中的一顆子樹，搜索時，把當前搜索樹中未處理的頂點加入一個堆棧，回溯時可以判斷棧頂到棧中的節(jié)點是否為一個強連通分量[3]。

該文利用Tarjan算法分析耦合系統(tǒng)形成的有向圖，不僅可以檢測出有向圖中的強連通分量也就是耦合系統(tǒng)中的代數環(huán)，還可以計算出有向圖中各個節(jié)點的賦值順序，利用這個賦值順序可以進行仿真初始化過程。

1.2.1 定義

DFN（u）為節(jié)點u搜索的次序編號（時間戳）;LOW（u）為u或u的子樹能夠追溯到最早的棧中節(jié)點的次序號。

由定義可以得出，當DFN（u）= LOW（u）時，以u為根的搜索子樹上所有節(jié)點為一個強連通分量[4]。

1.2.2 算法實現過程

（1）當檢索到未被記錄的點u時，DFN[u]=LOW[u]=time。

（2）每當搜索到一個點，把該點壓入棧頂，當u和v有邊相連時：

如果v不在棧中，DFS（v），并且LOW[u] = min{LOW（u），LOW（v）};

如果v在棧中，此時LOW[u] = min{LOW[u]，DFN[v]}。

（3）當DFN[u]=LOW[u]時，將它以及在它之上的元素彈出棧，此時，彈出棧的結點構成一個強連通分量。

（4）繼續(xù)搜索，直到圖被遍歷完畢。

2? 基于牛頓法解代數環(huán)

牛頓法是將非線性方程線性化的過程[5]。其核心思想是利用泰勒級數展開（忽略二階以上的項），通過不斷迭代尋找導數為0的解，求得近似解。

首先針對一元函數利用牛頓法進行求解進行簡單介紹。

2.1 一元函數推導過程

對于一元函數f（x）=0，將（x）在點x0處用泰勒公式進行展開（忽略二階以上的項）：

不斷進行迭代，當梯度的模等于零或者函數值下降小于指定閾值，得到函數解X*。

牛頓法利用逐次逼近的方法，計算機運算速度快、適合做重復性操作，讓計算機對一組指令進行重復執(zhí)行，在每次執(zhí)行這組指令時，都從變量的原值推出一個新值[6]。

牛頓法屬于二階收斂連，迭代速度相比簡單迭代要快很多。但是，牛頓法對初值比較敏感，若初值不合適，系統(tǒng)很有可能會出現不收斂的情況，使得求解效率降低;另外，函數必須具有二階偏導，計算量比較復雜。

3? 實驗結果對比

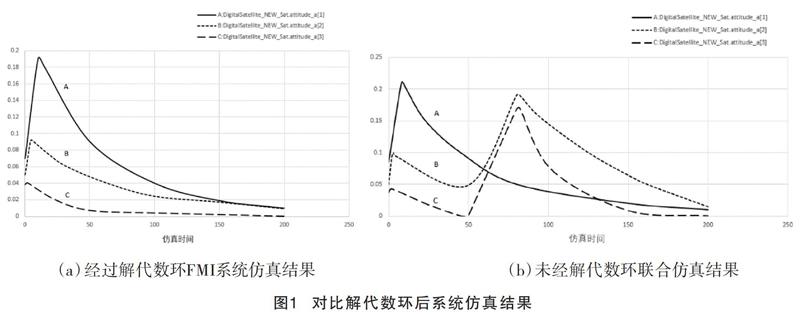
該次實驗案例中采用的實驗FMU模型有6個，分別為：衛(wèi)星動力學模型、姿態(tài)軌道控制器模型、動量輪安裝矩陣模型以及3個干擾模型。該實驗中選擇了動力學模型的3個輸出端口參數attitude_a[1]、attitude_a[2]、attitude_a[3]作為參考數據，這3個參數分別代表了衛(wèi)星在X軸、Y軸、Z軸3個方向的姿態(tài)角。

通過比較圖1實驗結果可以看出，解代數環(huán)的聯(lián)合仿真模型仿真結果和未進行解代數環(huán)的聯(lián)合模型仿真結果明顯不同，經過求解代數環(huán)的系統(tǒng)仿真過程更穩(wěn)定，仿真模型曲線更平滑，其所得結果也更精確。圖1仿真結果對比驗證了該文所述的代數環(huán)檢測和求解算法的有效性。在未來面對多學科模型耦合的之間存在的代數環(huán)問題提出了效果較好的解決方案。

4? 結語

隨著聯(lián)合仿真技術的快速發(fā)展，多學科之間的聯(lián)合仿真驗證過程，已經是開發(fā)系統(tǒng)性工程的必經之路。FMI聯(lián)合仿真標準定義了多學科聯(lián)合仿真的數據接口，打破了各學科仿真數據交互的壁壘。產品設計前的仿真可以有效降低產品開發(fā)成本和風險，同時可以促進各個學科領域的融合，提升科研成果轉化為生產力的速度。

該文闡述代數環(huán)解析算法在該分布式FMI聯(lián)合仿真系統(tǒng)中的應用實現過程，包括使用Tarjan算法進行代數環(huán)的檢測、基于牛頓迭代法求解代數環(huán)的應用。通過衛(wèi)星控制系統(tǒng)中相關仿真模型在系統(tǒng)中的仿真應用，驗證了該文所論述的代數環(huán)檢測和求解算法在分布式FMI仿真系統(tǒng)中的有效性和正確性。

參考文獻

[1] 姚逸程.基于FMI標準的動力總成模型在環(huán)虛擬車輛仿真研究[D].浙江大學，2017.

[2] 徐泰華.社交網絡中的子圖結構挖掘研究[D].西南交通大學，2019.

[3] 胡全義.基于鍵合圖的多領域統(tǒng)一建模與仿真技術研究[D].大連理工大學，2017.

[4] 楊維維.非線性方程組的算法及其在張量特征值的應用研究[D].南京航空航天大學，2017.

[5] 任露，黃穎為.基于牛頓迭代法的分形圖像研究[J].西安理工大學學報，2016（2）：247.

[6] 武海妮.改進的粒子群算法在求解非線性方程組中的應用[D].延安大學，2019.