在有效生成中涵育數學核心素養

福建省閩清縣第一中學 (350800) 林 婷 林青松

數學課堂是由“預設”和“生成”兩個部分組成的.“預設”是教師根據學情和教學目標有目的、有計劃地對課堂教學內容所進行的精心設計；“生成”是課堂預設的升華，使課堂教學“順學而導”，是教學生命力與真正價值所在.數學教學過程具有復雜多變性，需要教師具有敏銳的課程意識、足夠的教學智慧，寓有形的預設于無形的、動態的課堂教學中，營造出有利于學生發展的原生態課堂，為核心素養的落實找到出口與支點，從而完成數學教育立德樹人的目標.

1 運用“問題導學”，在探究中生成

教材是嚴肅的、權威的，但并非“至圣”的金科玉律，如果照本宣科，就算再高明的教師，也是不可能把課上得很精彩.因此，教師應潛心鉆研教材，在研究教材的基礎上遵循學生學習數學的認知規律，將教學內容“問題化”，提出既能激發學生學習興趣，又具有探究價值的“問題”，通過師生之間對“問題”的互動建構與合作交流，提升學生的“問題”意識，培養學生的探究能力，從而促進課堂生成.

案例1 人教A版必修第一冊“函數的零點與方程的解”教學片斷(引導學生探究零點存在性定理)

問題1 函數f(x)=x5+2x-1存在零點嗎？如果存在，是多少？

師：數學史上，數學家們希望能像求解低次方程那樣去解高次方程，但經過長期的探索，都沒有得到解決.1824年，挪威天才數學家阿貝爾(N.H.Abel，1802—1829)成功地證明了五次及以上的方程沒有根式解.那么，我們能否利用別的方法判斷函數有否零點呢？

生1：可利用函數圖象的性質判斷函數的零點．

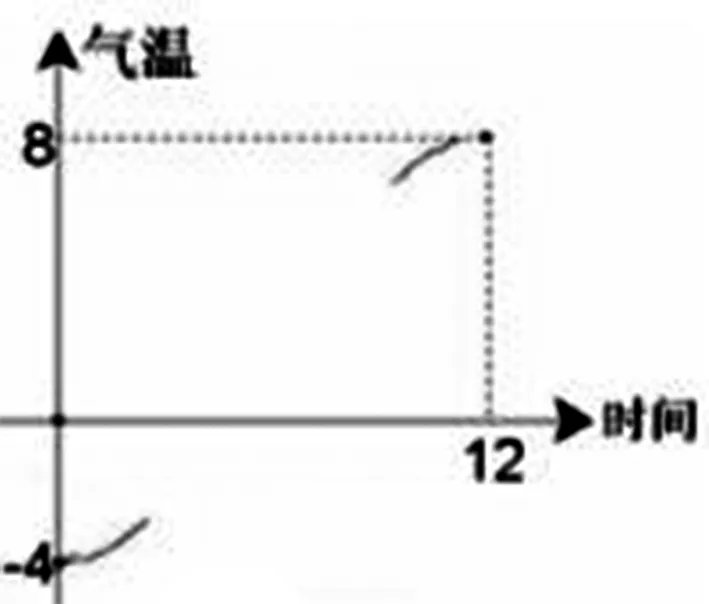
圖1

問題2 圖1為某地區從0時到12時的溫度變化圖，假設氣溫是連續變化的，請用兩種不同的曲線將圖形補充成完整的函數圖象.在這段時間內，是否一定有某時刻的溫度是0℃？為什么？

教師引導學生設計“兩種方法”，激發了學生的探究熱情.他們大膽嘗試、操作.—種、兩種、三種……，課堂出現了“未曾預約”的生成，其中包括在區間(a，b)內只有單一零點的函數圖象(單調或不單調的)，也有多個零點的函數圖象.教師對學生的各種畫法進行展示(限于篇幅，文中只給出圖2(1)、圖2(2)兩種連接方法).

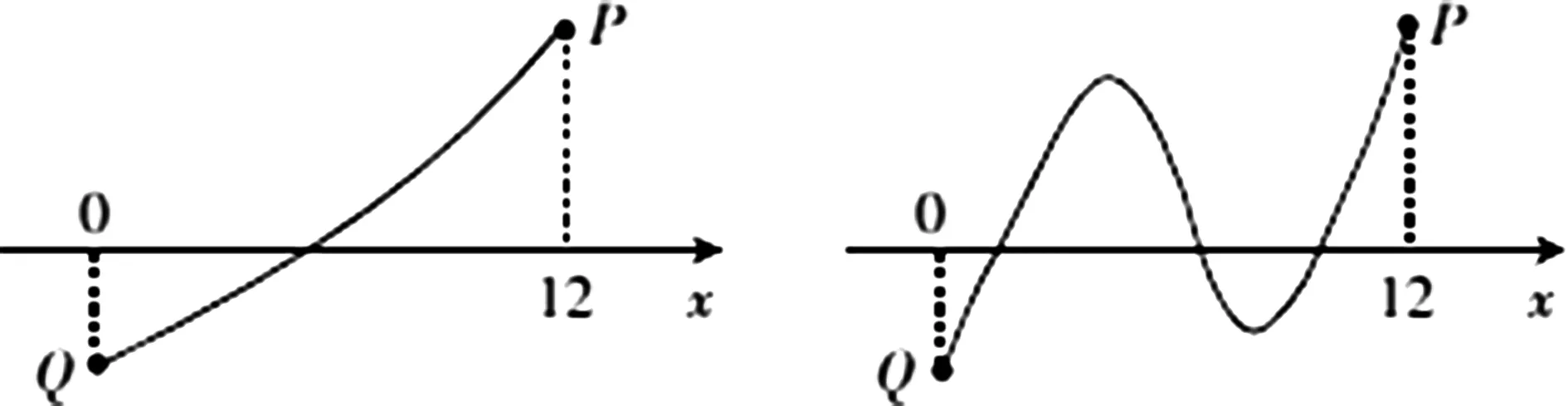
圖2(1) 圖2(2)

問題3 若0時的溫度與12時的溫度都在零上(下)，是否一定有溫度為0℃的時刻？

問題4 對于一般的函數y=f(x)，在區間[a，b]上有f(a)·f(b)<0，那么函數y=f(x)在(a，b)內必存在零點嗎？

學生議論起來，一部分學生認為“存在零點”，另一部分則回答“不一定”.

師：請大家舉例說明.

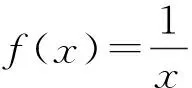
問題5 對于一般的函數y=f(x)，滿足什么條件時，函數f(x)在區間(a，b)內一定有零點？

(教師運用“問題導學”，讓學生經過火熱的思考，水到渠成地獲得了函數零點存在定理.)

問題6 請舉例回答如下問題：

(1)若函數f(x)在區間[a，b]上的圖象是一條連續不斷的曲線，且滿足f(a)·f(b)>0，則f(x)在(a,b)內有零點嗎？

(2)若函數f(x)在區間[a，b]上的圖象是一條連續不斷的曲線，且滿足f(a)·f(b)<0，函數f(x)在(a,b)內是否只有一個零點？

(3)若函數f(x)在區間[a，b]上的圖象是一條連續不斷的曲線，且滿足f(a)·f(b)<0，還需滿足什么條件時，函數f(x)在區間(a,b)內恰有一個零點？

(4)若函數f(x)在區間[a，b]上的圖象是一條連續不斷的曲線，且在區間(a,b)內恰有一個零點.是否必有f(a)·f(b)<0？

教師從“溫度曲線”這一生活常識出發，讓學生直觀感受某個時間段上溫度的變化，“區間”、“連續不斷”、“異號”等要素一應俱全，為學生提供了探究性學習的好素材.通過設計環環相扣的“問題”引導學生探究，使學習過程成為在教師引領下“再創造”的過程，真正實現了“教教材”到“用教材教”.課堂靈動充溢，順理成章地歸納、抽象、概括出問題的本質屬性，生成了“函數零點存在定理”，提升了學生的直觀想象、數學抽象、邏輯推理等核心素養.

2 善待錯誤資源，在辨析中生成

教師在課堂教學中“有意”或“無意”的“錯誤”，學生認知過程中的偏差或失誤，我們稱之為教學中的“錯誤資源”.由于學生的知識水平、思維方式等方面都存在著差異，課堂生成難免存在一定的偏頗與缺陷.教師應樹立正確的“錯誤”觀，并有效利用學生的錯誤，引導學生質疑、討論，促使學生通過比較、分析、反思，不斷深化知識學習，完善認知結構，提高對錯誤的“免疫力”.

案例2高中數學新教材人教A版必修第一冊“基本不等式的應用”教學片斷

對于上述錯解，若不加以詳細分析就將其束之高閣，必然會挫傷學生的自信心.因此教師因勢利導，引導學生從失敗走向成功.

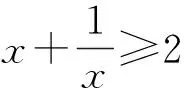
解決了以上問題之后,教師圍繞問題特征引導學生進一步探究.

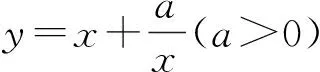
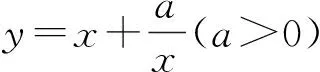
多好的生成性資源啊！在課堂教學中，教師應善于利用“錯誤資源”，探尋錯誤背后所隱含的教育價值，使之成為新的教學契機.通過互動交流，深度探究，促使學生在正確與錯誤的矛盾中碰撞，引發知錯、改錯、防錯的良性反應，對數學學習產生積極的情感體驗，并從中審視與體驗，幫助學生建構起正確的認知結構，在“錯誤—發現—探究—歸真”的良性循環中提升思維品質，涵育數學抽象、邏輯推理、數學建模、數學運算等核心素養.

3 引導反思評價，在感悟中生成

數學知識的學習過程既需要有一個對所學知識的掌握、加工與理解的認識過程，也需要有一個對該過程進行積極的監控、調節的反思過程.引導學生解后反思，對自己的思維過程進行再驗證、再認識，在不斷地提出問題又不斷地解決問題的過程中，促使學生對數學思想方法從感性認識上升到理性認識，從而迸發思維的靈性，為演繹高效課堂、培養學生的關鍵能力創設良機.

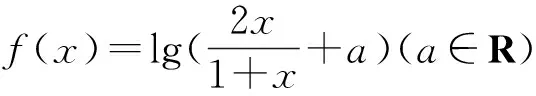
(這是我校高三數學第一輪復習單元考試的一道填空題，題目不難，但錯的很多.)

講評課上，教師請一位答錯的學生說說如何得出結果.

生1：由于函數f(x)為奇函數，因此f(0)=0，得lga=0，故a=1.

為了讓學生從根本上認識錯因，改正錯誤，教師引導學生反思：

反思1 求出a的值后，我們還應該考慮什么？

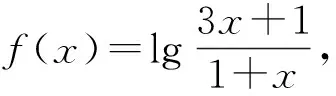
“這結果與已知條件矛盾！”學生一臉疑惑：“利用f(0)=0怎么會出錯呢？”

教師不動聲色，進一步引導學生反思：

反思2f(0)=0對所有奇函數都成立嗎？若不是，請舉出反例.

學生通過反思，體會到：由于函數f(x)中含有參數a，因此無法確定其定義域是否包含0.在未確定函數定義域是否含有0時，不能盲目應用f(0)=0求參數的值.

反思4 滿足什么條件的函數才是奇函數呢？

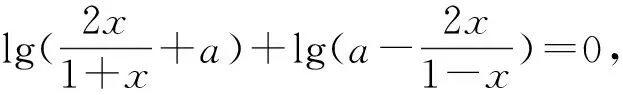
反思5 本題對今后解決這一類問題有什么啟發呢？

生3：(1)解決函數問題應該優先考慮定義域，在a沒有確定的情況下，無法確定x=0是否在定義域內；(2)判斷函數的奇偶性用定義求解最可靠.

師：非常好！由以上解法我們還可以得到一個啟示：對于等式恒成立問題，可以運用待定系數法求解參變量的值.

案例3中，教師利用學生的錯解作為反面教材，引導學生進行反思，通過相互交流，深層思考.師生在互動對話中經歷了從錯誤走向正確認識的過程，不僅加深了學生對概念內涵的認識，而且能促使學生的學習活動成為一種有目標有策略的主動行為，不斷地發現問題，提出問題，生成新的問題的“生長點”，推動學生從淺層學習不斷走向深度學習.

總之，只有合理、恰當地處理好預設與生成的關系，科學而藝術地把握動態生成資源，使之成為學生掌握知識、培養情感、提升能力的生長點，才能打造出基于學生主體的孕育數學核心素養的課堂教學.