對一堂優(yōu)質(zhì)評比課的幾點思考

浙江省寧波市第四中學(xué) (315016) 蔣亞軍

貴州省安龍縣2020年春季高中數(shù)學(xué)優(yōu)質(zhì)課評比在安龍一中舉辦，筆者作為支教教師有機會參與到聽課環(huán)節(jié)，課題為《1.1.2余弦定理(第一課時)》.參賽的六位選手精心準(zhǔn)備，呈現(xiàn)了精彩的設(shè)計.本文以聽課者的視角對情境引入、定理推導(dǎo)和課堂小結(jié)三個環(huán)節(jié)進行了以下幾點思考.

思考1：如何創(chuàng)設(shè)合適的情境

情境引入1：以杭州淳安的千島湖圖片，設(shè)計三個小島分別是A、B、C，一名游客想從A島直接到C島，已知AB=6km，AC=3km，∠B=120°，卻不知道BC距離究竟是多長，你能幫他算一算嗎？

情境引入2：多彩貴州有很多隧道,技術(shù)人員在修建每個隧道前(打通前)都需要確定隧道長度.其方法是:先在地面上選一適當(dāng)位置A，量出A到山腳B、C的距離,再利用測量儀器測出的大小,最后通計算求出山腳的長度BC.大家想知道工程技術(shù)人員是怎樣計算出來的嗎?

評注：《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年)解讀》指出，基于核心素養(yǎng)的教學(xué)，要特別重視情境的創(chuàng)設(shè)和問題的提出.情境可以包括：現(xiàn)實情境、數(shù)學(xué)情境、科學(xué)情境[1].參賽的六位選手都是從現(xiàn)實情境出發(fā)，將生活中的問題抽象轉(zhuǎn)化為數(shù)學(xué)的問題，聯(lián)系學(xué)生已有的知識正弦定理，發(fā)現(xiàn)正弦定理不能解決這類問題，產(chǎn)生認(rèn)知上的沖突，激發(fā)學(xué)生的求知欲，順利引入本課題余弦定理.相比較很多學(xué)生對千島湖的不熟悉，引入2更貼近學(xué)生的生活，通過教師有意識的講解，學(xué)生對美好家鄉(xiāng)美好生活感到自豪.解三角形的產(chǎn)生和發(fā)展就是解決現(xiàn)實生活中測量三角形的邊和角，使幾何與代數(shù)有機的結(jié)合起來，進而促進三角函數(shù)的發(fā)展，正弦定理和余弦定理不僅是解決三角形中定邊定角的有力工具，而且是對初中全等三角形的定性判斷上升到了定量計算.遺憾的是很少有選手從整體教學(xué)的角度去思考這一問題，幫助學(xué)生編織相互聯(lián)系的知識網(wǎng)絡(luò).

思考2：余弦定理公式的推導(dǎo)

在△ABC中,已知AB=c,AC=b,角A,求BC邊a.

圖1

公式推導(dǎo)3：(1)當(dāng)∠A是直角時，a2=b2+c2=b2+c2-2bccos90°=b2+c2-2bccosA.

圖2

(2)當(dāng)∠A是銳角時,如圖2,過點C作CD⊥AB,交AB于點D,則在Rt△ACD中,AD=bcosA,CD=bsinA.從而,BD=AB-AD=c-bcosA.在Rt△BCD中,由勾股定理可得BC2=BD2+CD2=(c-bcosA)2+(bsinA)2=c2-2cbcosA+b2，即,a2=b2+c2-2bccosA.

圖3

(3)當(dāng)∠A是鈍角時,如圖3,過點C作CD⊥AB,交BA延長線于點D,則在Rt△ACD中AD=bcos(π-A)=-bcosA中,CD=bsin(π-A)=bsinA.從而,BD=AB+AD=c-bcosA.在Rt△BCD中,由勾股定理可得BC2=BD2+CD2=(c-bcosA)2+(bsinA)2=c2-2cbcosA+b2,即a2=b2+c2-2bccosA.

綜上(1),(2),(3)可知,a2=b2+c2-2bccosA成立.

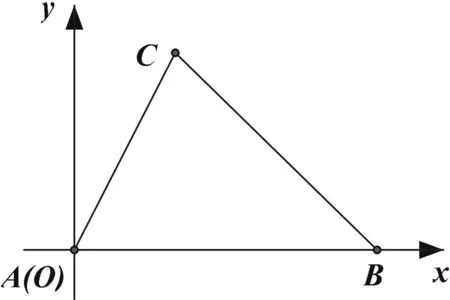
圖4

公式推導(dǎo)4：建立平面直角坐標(biāo)系(如圖4),則由題意可得點A(0,0),B(c,0),C(bcosA,bsinA),再由兩點間距離公式可得a2=(c-bcosA)2+(bsinA)2=c2-2cbcosA+b2.即a2=b2+c2-2bccosA.

思考3：設(shè)計有新意的課堂小結(jié)

課堂小結(jié)1：通過本節(jié)課的研學(xué)習(xí)，同學(xué)們學(xué)到了那些知識和方法？有何體會？(學(xué)生自我總結(jié)，教師適時補充完善)

1.余弦定理及其推論.

2.余弦定理可解決兩類解三角形問題：一是已知三邊，二是已知兩邊及其夾角.

3.用向量法證明余弦定理，體現(xiàn)了數(shù)形結(jié)合思想.

課堂小結(jié)2：在師生共同完成知識、方法、數(shù)學(xué)思想的小結(jié)后，教師賦打油詩一首：

解決三角形，邊角是關(guān)鍵

正弦加余弦，余弦可求邊

正弦邊角化，定角用余弦

綜合正余弦，三角化簡便

課堂小結(jié)3：以框圖的形式展現(xiàn)本節(jié)課的知識和學(xué)習(xí)的脈絡(luò).

評注：課堂小結(jié)是對本節(jié)課學(xué)習(xí)的知識、方法、技能和數(shù)學(xué)思想的總結(jié)，對比三種不同的總結(jié)方式，會發(fā)現(xiàn)：課堂小結(jié)1是教師經(jīng)常采用的一種模式，通過學(xué)生自主回顧總結(jié)和教師適時補充完善，有利于學(xué)生對學(xué)習(xí)內(nèi)容的有效整理，培養(yǎng)學(xué)生的表達(dá)能力；課堂小結(jié)2打油詩一首更是增添新意，引起學(xué)生的興趣，朗朗上口的語言，更利于學(xué)生理解和掌握解三角形時的方法選擇；課堂小結(jié)3以圖形的形式再次展現(xiàn)本節(jié)課的學(xué)習(xí)過程，條理清晰思路明確，比文字語言描述更加生動，并且提出一個思考題，學(xué)生帶著問題離開課堂，通過查找資料、分工合作，有效地將課堂延伸，激發(fā)學(xué)生的學(xué)習(xí)熱情和學(xué)習(xí)興趣.

數(shù)學(xué)學(xué)科核心素養(yǎng)是數(shù)學(xué)課程目標(biāo)的集中體現(xiàn)，是具有數(shù)學(xué)特征的思維品質(zhì)、關(guān)鍵能力，以及情感態(tài)度價值觀的集中體現(xiàn)，是在數(shù)學(xué)學(xué)習(xí)和應(yīng)用的過程中逐步形成和發(fā)展的[2].而核心素養(yǎng)的培養(yǎng)，既要使學(xué)生習(xí)得數(shù)學(xué)知識，更要讓學(xué)生經(jīng)歷數(shù)學(xué)研究的過程，體驗隱藏在背后的數(shù)學(xué)思想方法以及研究方法[3].教師在課堂教學(xué)中應(yīng)當(dāng)結(jié)合教學(xué)內(nèi)容，設(shè)計合適的問題情境，引導(dǎo)學(xué)生用數(shù)學(xué)的語言表達(dá)問題，培養(yǎng)發(fā)現(xiàn)和提出問題的能力，分析和解決問題的能力，在余弦定理公式的推導(dǎo)過程中一點要舍得花時間讓學(xué)生思考和探索，給予學(xué)生展示思維活動的機會和平臺，激發(fā)學(xué)生多角度深層次的思考問題，關(guān)注學(xué)生對數(shù)學(xué)知識真正的理解.從而達(dá)到學(xué)生對“冷艷”的數(shù)學(xué)進行“火熱”的思考的目的.有新意的設(shè)計課堂小結(jié)，如打油詩形式、框圖形式以及設(shè)計成一個卡通圖案，會給學(xué)生一種視覺上的沖擊，產(chǎn)生新鮮感，促進學(xué)生的理解和掌握.