大懸挑空間網架屋蓋—樹狀編織筒殼支承結構的穩定性研究

周鼎 吳岸

1.武漢市政工程設計研究院有限責任公司 430070

2.武漢理工大學 430070

引言

近年來，空間網架結構憑借其輕質高強、生產安裝便利、外觀優美等特點，廣泛應用于大跨建筑結構的屋蓋中［1－3］。作為大跨空間網架的支承結構，樹狀仿生結構的應用，極大地增加了大跨空間結構建筑面積的利用率，使支承節點域內的應力分布更加均勻［4－6］。

然而大跨度空間網架及其樹狀支承結構的缺點是節點桿件受力復雜，結構整體穩定性差，極易發生整體傾覆，因此針對該類建筑結構的穩定性分析顯得十分重要。目前，國內外學者針對空間網架結構的穩定性進行了大量的研究，并取得了較多的成果。Dhatt和Batoz等［7］在非線性結構穩定問題的牛頓法基礎上提出了位移增量法。He等［8］對圓柱形網架結構的穩定性進行研究，分析了結構可能出現的屈曲模態以及不同條件下的極限承載力。楊倫［9］對某機場T3 航站樓網架屋蓋進行了特征值屈曲分析、幾何線性屈曲分析和彈塑性全過程穩定性驗算，結果表明該網架屋蓋具有一定的延性，穩定性滿足要求。劉記雄等［10］利用SPA2000 對開洞和不開洞網架結構分別進行了線性和非線性屈曲分析，研究了開洞大小及位置對網架結構穩定性的影響。袁棪等［11］以某大學體育館平板網架結構為研究對象，從整體穩定性、溫差作用兩個方面對整體結構（帶支撐）和上部結構單獨計算的整體工作性能進行對比分析。結果表明，單獨計算的上部網架結構所得的穩定性承載力較大，偏于不安全。

本文在上述研究基礎上以某大懸挑空間網架屋蓋—樹狀編織筒殼支承結構為研究對象，對其穩定性進行研究。采用MIDAS 及ABAQUS 對結構進行線性、幾何非線性和幾何材料雙重非線性屈曲分析，觀察其屈曲模態及失穩破壞形式。并根據屈曲模態結果確定失效構件，完成關鍵構件失效后的穩定性計算。

1 工程概況

1.1 工程背景

廣東省某大懸挑空間網架屋蓋及其樹狀編織筒殼支承結構，其屋蓋采用局部雙層具有明顯曲率的大懸挑空間網架結構。網架為四角錐網架結構，網架支承最大跨度60m，最大懸挑23.5m，高度20m。網架結構中部的樹形編織體支承是由12 個V 型圓鋼管豎向通過多級分支三維展開，呈樹狀結構相貫交織在一起，形成空間筒殼結構如圖1 所示。其節點形式呈X型、Y型和根部作用的V型。材料屬性見表1。

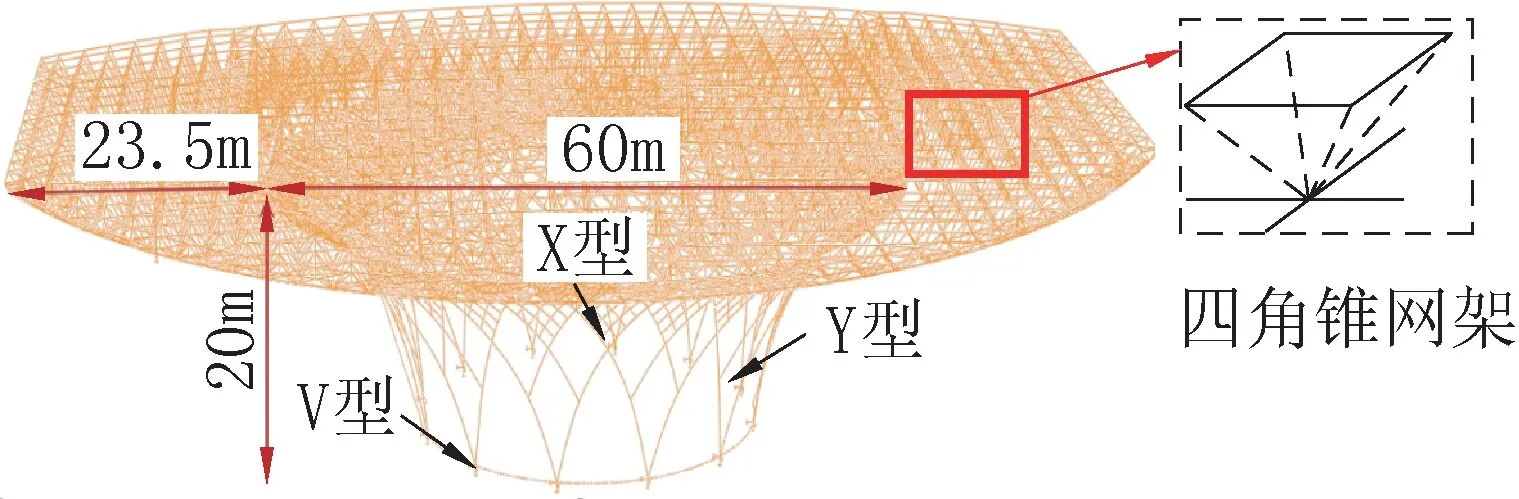
圖1 大懸挑空間網架屋蓋—樹狀編織筒殼支承結構Fig.1 Large cantilevered grid roof with treelike braided cylindrical shell

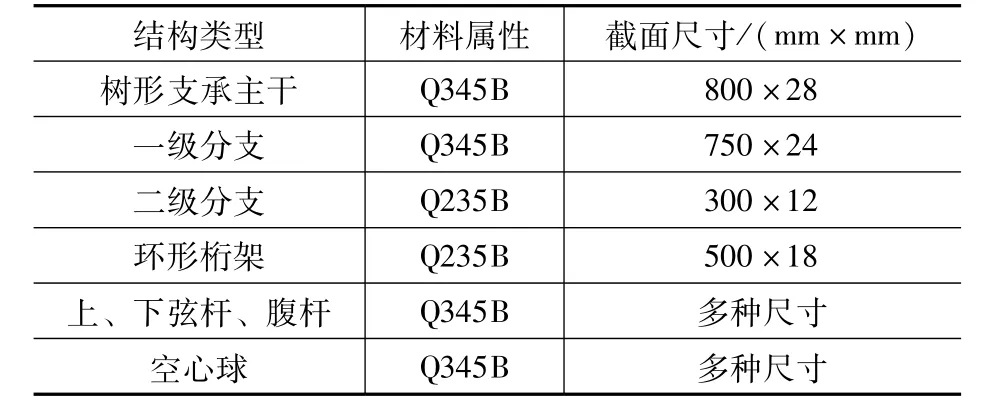
表1 結構材料Tab.1 Structural materials

1.2 荷載組合

結構抗震設防烈度為7 度，設計基本地震加速度為0.10g，地面粗糙度類別為B 類。根據實際情況確定結構計算的荷載取值。（1）網架屋面恒荷載標準值：上弦層0.75kN／m2、下弦層0.30kN／m2；（2）網架屋面活荷載標準值：上弦層0.50kN／m2、下弦層0.50kN／m2；（3）基本風壓：0.65kN／m2（100 年重現期）、0.6kN／m2（50年重現期）；（4）基本雪壓：無。

大懸挑空間網架屋蓋—樹狀編織筒殼支承結構根據《建筑結構荷載規范》（GB 50009—2012）［12］進行荷載組合，得到的靜力荷載工況組合如表2 所示。

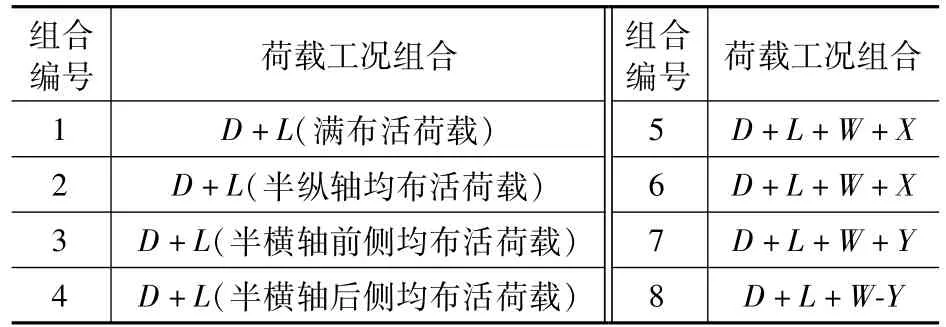
表2 荷載組合Tab.2 Load combination

2 線性屈曲分析

線性屈曲分析是對理想結構的整體穩定分析，不包含幾何缺陷和材料的非線性，其得到的屈曲臨界荷載反映的是結構極限荷載的上限值。通常在進行整體結構的非線性分析之前，需要引入線性屈曲模態作為初始缺陷的分布形式，因此非常有必要進行線性屈曲分析。

2.1 最不利荷載組合

用midas Gen軟件按照表2 中的8 種工況組合對結構進行線性屈曲分析，以獲得不同荷載工況下的屈曲荷載系數。表3 給出了8 種工況下結構的前5 階線性屈曲荷載系數。

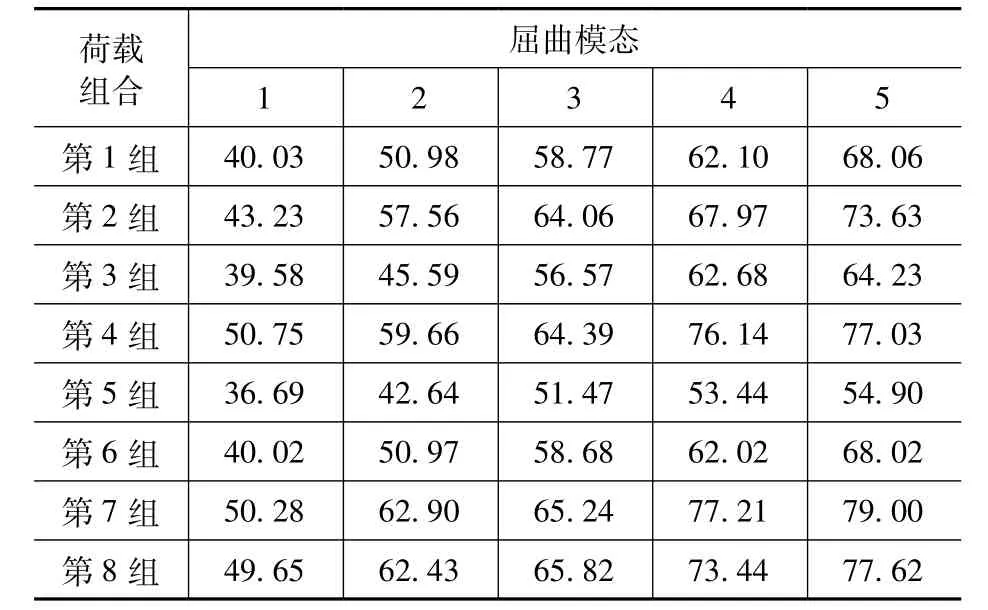
表3 8 種工況下的前5 階線性屈曲荷載系數Tab.3 Linear buckling load coefficients of the first five orders under 8 working conditions

屈曲臨界荷載等于屈曲臨界系數與所施加荷載的乘積，即屈曲臨界系數越小，其整體穩定性越低。由表3 結構前5 階屈曲臨界荷載系數的趨勢可知，第5 組荷載組合是最不利工況組合。

2.2 失穩模態

圖2 為ABAQUS 計算的荷載組合5（D＋L＋W＋X）作用下結構前5 階線性屈曲失穩模態。從圖中可知，前5 階屈曲失穩主要發生在屋蓋網架結構以及樹狀支承的前側，其中以樹狀支承結構節點處更為明顯。主要是由于結構在第5 種荷載組合下，橫向風荷載比較強烈，而結構的橫向剛度較弱，導致該部位率先發生失穩。

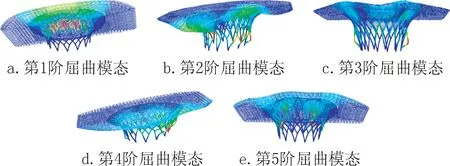
圖2 屈曲模態Fig.2 Buckling mode diagram

通過對比ABAQUS 與MIDAS 計算的前5 階線性屈曲荷載系數（表4），發現屈曲荷載系數的變化規律基本一致，皆隨模態階數的增加而增加。前5 階模態屈曲荷載系數的最大誤差在8%以內，平均誤差為5.71%，驗證了所采用的模型及計算方法的正確性，計算模型及結果可用于后續的非線性屈曲分析。

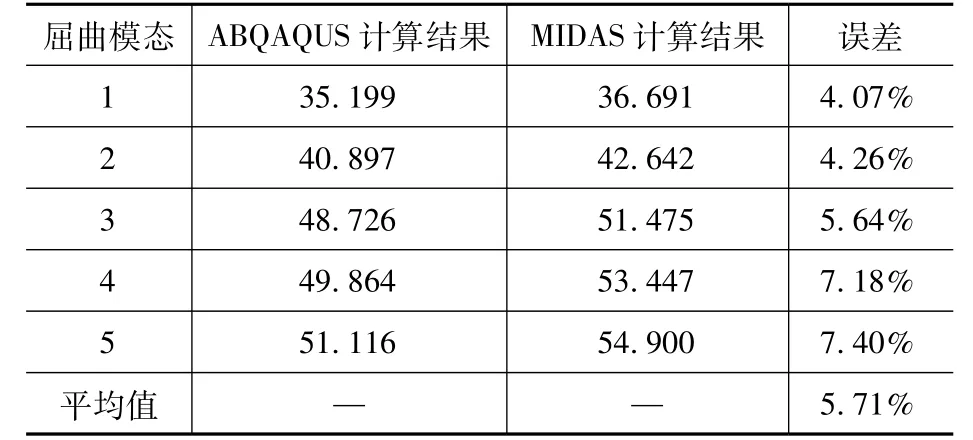
表4 前5 階屈曲模態對比Tab.4 Comparison of the first five buckling modes

3 非線性屈曲分析

3.1 幾何非線性屈曲分析

目前在進行結構幾何非線性屈曲分析時，一般采用一致模態缺陷法，即用最低階的屈曲模態來模擬初始幾何缺陷對結構的影響。研究表明初始缺陷達到空間最大跨度的1／300 時，缺陷對結構承載力才會產生較大影響。初始缺陷取L／300、L／200、L／100 即200mm、300mm、600mm（L為最大跨度60m）。

表5 為在第5 組最不利荷載組合工況下利用ABAQUS和MIDAS 計算的不同初始缺陷的幾何非線性屈曲系數。從表中發現，屈曲系數隨著初始缺陷取值的增大而減小；初始缺陷對結構幾何非線性穩定承載力影響較小，承載力下降5%～10%。MIDAS和ABAQUS的計算結構誤差在6%以內，說明兩種軟件計算的幾何非線性結果較為合理，同時也說明該結構為缺陷不敏感結構。

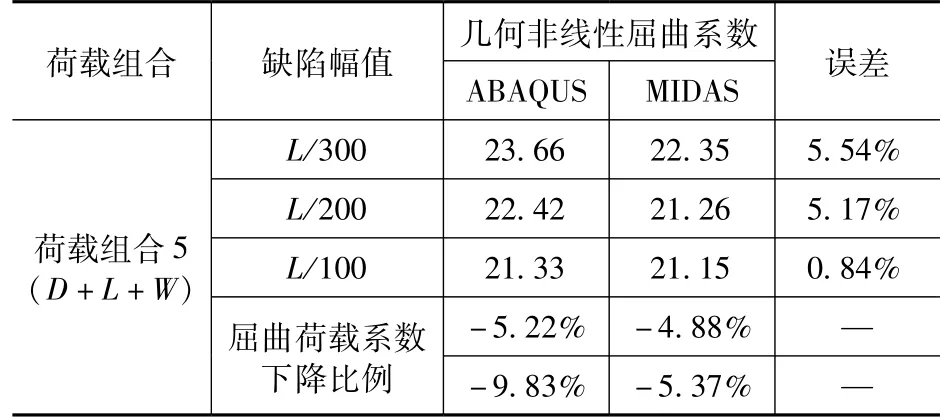
表5 幾何非線性屈曲荷載系數Tab.5 Geometric nonlinear buckling load coefficient

圖3 為利用ABAQUS計算荷載組合5 工況下的幾何非線性屈曲臨界荷載系數與豎向最大位移之間的關系曲線。從圖中可以發現，荷載組合5工況下帶缺陷結構的幾何非線性屈曲分析（L／300）得到的穩定性承載力為基本荷載的23.66倍，表明結構具有較好的穩定性；屈曲系數在達到臨界點之前，豎向位移隨著荷載的增大而增大。

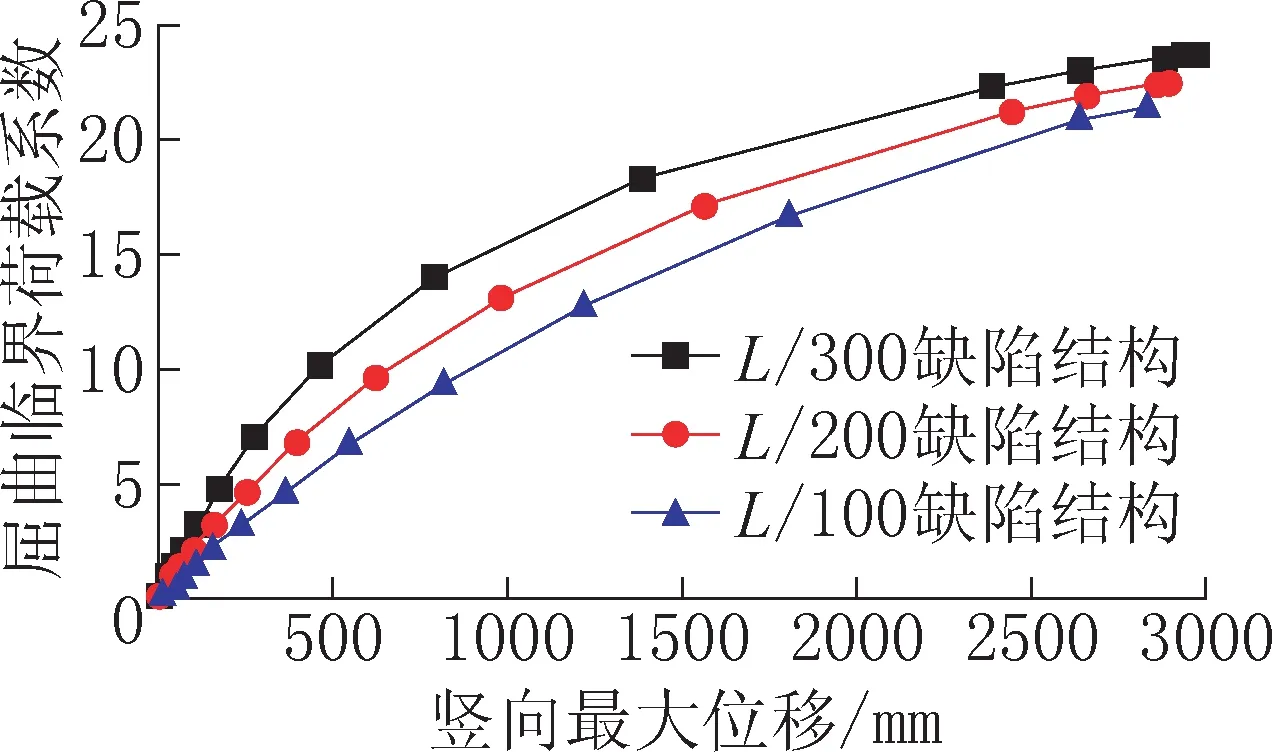
圖3 幾何非線性屈曲臨界荷載系數-豎向最大位移曲線Fig.3 The curve of geometric nonlinear buckling load coefficient and vertical maximum displacement

3.2 雙重非線性屈曲分析

對于網架結構這類厚度相對于跨度很小的柔性結構，幾何非線性分析雖然能反映其整體的穩定性，但不能排除網架結構部分桿件在結構達到臨界荷載之前就進入彈塑性狀態。因此，對于重要結構，既考慮幾何非線性又考慮材料非線性的雙重非線性分析最能反映結構的真實情況。

表6 為采用ABAQUS對結構進行雙重非線性屈曲分析的屈曲荷載系數，荷載選擇第5 組最不利荷載組合工況，初始缺陷值分別取L／300、L／200、L／100，鋼材采用雙折線模型。從表中可以發現，結構的雙重非線性屈曲荷載系數明顯小于幾何非線性荷載系數，造成二者計算結果相差較大的原因主要是由于結構發生屈曲時產生了較大的變形，在考慮材料非線性后，屈曲部位桿件應力超過了材料屈服應力進入塑性階段。

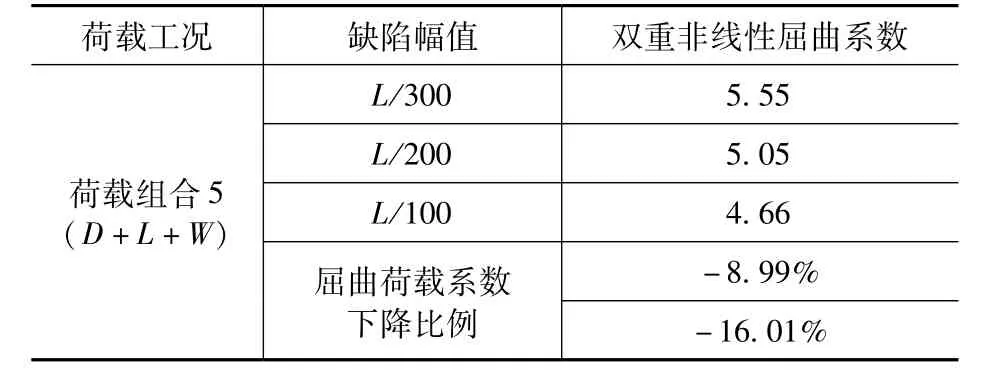
表6 雙重非線性屈曲荷載系數Tab.6 Double nonlinear buckling load coefficients

從圖4 不同缺陷下雙重非線性屈曲荷載系數隨豎向位移的變化曲線可知，屈曲系數隨著初始缺陷的增大逐漸減小，在結構達到臨界荷載之前均隨著豎向位移的增加而增加。初始缺陷的變化使非線性承載力降低8%～16%，說明結構為缺陷不敏感結構。

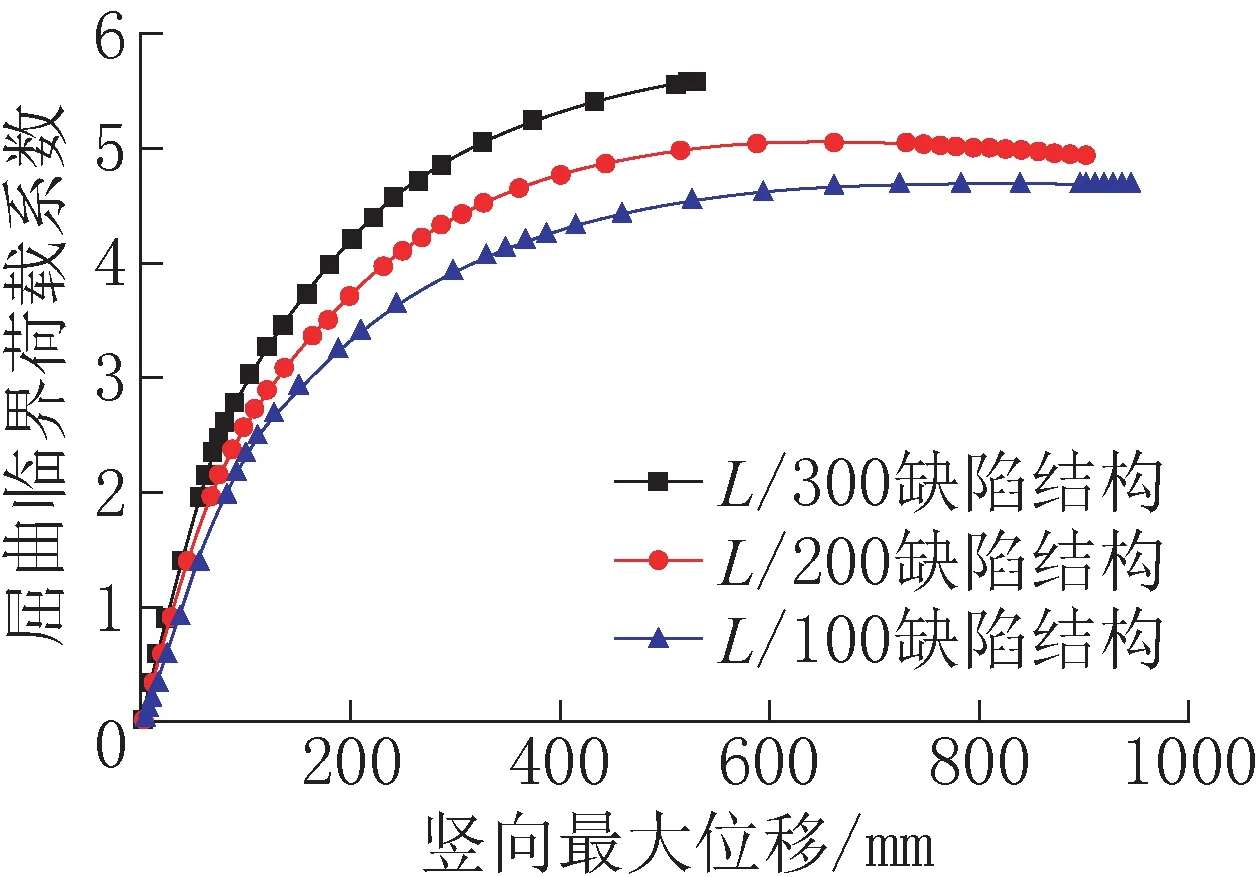
圖4 雙重非線性屈曲臨界荷載系數-豎向最大位移曲線Fig.4 The curve of double nonlinear buckling load coefficient and vertical maximum displacement

3.3 關鍵構件失效的雙重非線性屈曲分析

由前文結構的屈曲模態分析可知，結構在第5 種最不利荷載組合工況下屈曲失穩主要發生在屋蓋網架結構以及樹狀支承的前側，其中以樹狀支承結構節點處更為明顯。因此，在對屈曲模態失穩形式研究的基礎上，總結出以下4 種關鍵構件的失效可能會對結構整體穩定性產生較大的影響：失效構件1 為樹狀編織筒殼結構前側Y型節點的主干構件；失效構件2 為其相鄰的Y型節點的分支構件；失效構件3為X型節點的分支構件；失效構件4 為屋蓋桁架下部支承構件。如圖5 所示。在進行失效桿件的雙重非線性屈曲分析時，對失效的關鍵構件用非常小的剛度進行模擬，初始缺陷取L／300，鋼材采用雙折線模型。

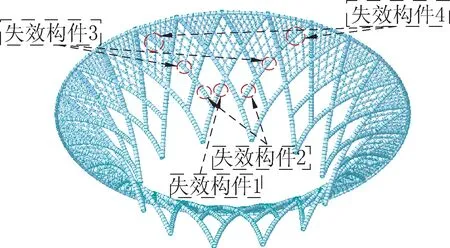
圖5 關鍵構件失效布置Fig.5 Failure diagram of key components

圖6 繪制了在第5 組荷載組合工況下，不同關鍵部位構件失效后的雙重非線性屈曲荷載系數與豎向最大位移的關系曲線，并將得到的屈曲荷載系數列于表7。從圖6 和表7 中可以發現，不同部位關鍵構件的失效均會影響結構受力性能，會使結構穩定性下降。樹狀編織筒殼結構前側Y型節點的主干構件失效會導致屈曲臨界荷載降低約15.5%，與其相鄰的Y型節點的分支構件、X型節點的分支構件和屋蓋桁架下部支承桿件的失效導致屈曲臨界荷載分別降低約9.73%、9%和4.14%。說明Y型節點主干構件的失效對結構穩定性的影響最大，通過增強該樹狀結構主干可以提高結構的承載力。

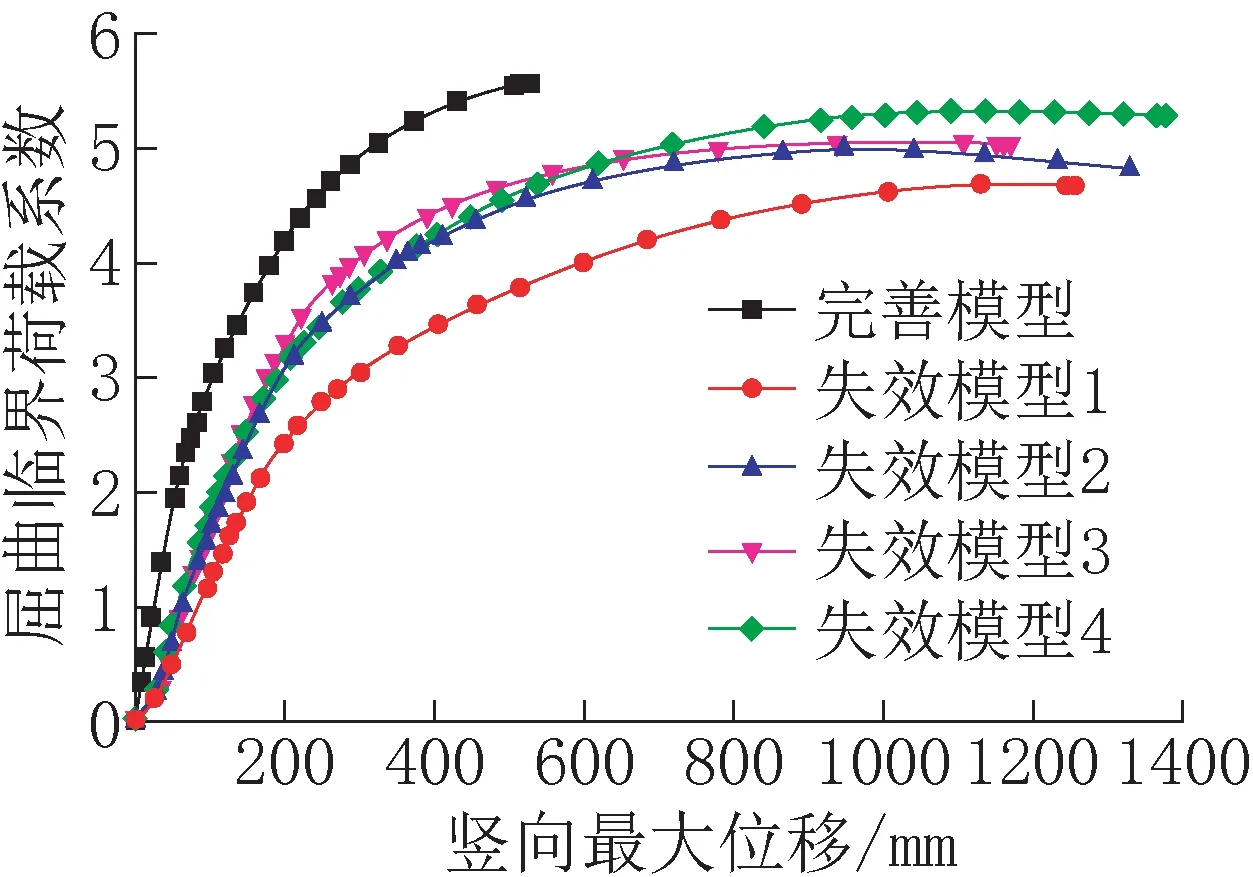
圖6 關鍵構件失效的屈曲荷載系數-豎向最大位移曲線Fig.6 Buckling load coefficient and vertical maximum displacement curve of key components failure

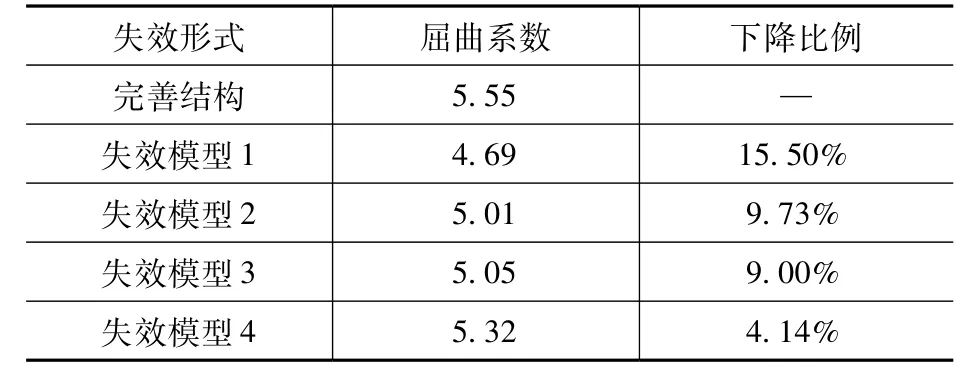
表7 關鍵構件失效下荷載屈曲系數Tab.7 Load buckling coefficient of key component failure

4 結論

1.利用ABAQUS和MIDAS 對結構進行線性屈曲分析發現，結構在第5 組荷載組合工況下屈曲荷載系數最小，可以作為最不利荷載組合工況。該工況下屈曲失穩主要發生在屋蓋網架結構以及樹狀支承的前側，其中以樹狀支承結構節點處更為明顯。

2.對結構進行幾何非線性屈曲分析發現，初始缺陷對結構幾何非線性穩定承載力影響較小，承載力下降在5%～10%，說明該結構為缺陷不敏感結構。

3.對結構進行雙重非線性屈曲分析發現，考慮幾何、材料雙重非線性相較于幾何非線性，結構的屈曲荷載系數有明顯下降。其中初始缺陷的變化使非線性穩定承載力降低8%～16%。

4.對結構關鍵構件失效的雙重非線性屈曲分析發現，不同部位關鍵構件的失效均會影響結構受力性能，會使結構穩定性下降，其中以樹狀支承結構主要受力的Y型節點的主干失效對結構穩定性影響最大，通過增強該樹狀結構主干可以提高結構的承載力。