基于卷積神經網絡和MPGA-LM算法的陣列側向測井快速反演方法

吳易智， 范宜仁*， 巫振觀， 鄧少貴，張盼， 陳詩宇， 尹中旭

1 中國石油大學(華東)地球科學與技術學院， 青島 266580 2 海洋國家實驗室海洋礦產資源評價與探測技術功能實驗室， 青島 266237

0 引言

憑借著較高的分辨率以及豐富的探測信息，陣列側向測井被廣泛用于大斜度井/水平井的油氣藏評價(Rasmus, 1982; Itskovich et al., 1998; 鄧少貴等, 2010).然而在致密性儲層電阻率評價過程中，由于地層裂縫和薄互層發育以及沉積顆粒的大小、磨圓不一等因素，導致儲層各向異性特征明顯，測井響應復雜，為油氣層的識別與評價帶來一定的難度(Salazar and Torres-Verdín, 2009; 高杰等, 2010; Gao et al., 2013).因此，如何從測井響應中準確提取地層真實電阻率成為電測井領域亟待解決的難題之一.

非線性反演技術可以充分考慮井眼、侵入等因素對測井響應的影響，成為大斜度井/水平井井旁電阻率剖面重構的有效手段(Nam et al., 2010; Wang, 2011; 潘克家等, 2013).其算法包括確定性算法和隨機類算法.其中，確定性算法主要基于最小二乘理論，其核心在于通過不斷迭代模型參數的方式使得模擬數據與觀測數據的偏差最小(Osman and Laporte, 1996; Habashy and Abubakar, 2004; Madsen et al., 2004; 姚東華等, 2010; Hu and Fan, 2018)，該類算法包括最速下降法、高斯牛頓法以及列文伯格馬奎特法等(Anderson, 2001).由于能夠有效消除圍巖、層厚和侵入等因素的影響，確定性算法被廣泛用于2D陣列側向測井資料的快速處理(Wang et al., 2009; 王磊等, 2018).然而對于斜井各向異性等三維地層環境而言，正演效率過低，導致反演迭代過程中雅可比矩陣或海森矩陣求取耗時，同時該類算法對初值依賴性強，易陷于局部極小值，不利于陣列側向測井資料的快速精確處理(Pardo et al., 2007; Dubourg et al., 2017; Wu et al., 2020).不同于確定性算法，隨機類算法由單點或多點啟發，搜索步長和方向具有隨機性，可以在求解域內全空間搜索，全局尋優能力強，進而能夠提高資料處理精度，此類算法包括粒子群優化算法、模擬退火算法以及差分進化算法等(Eiben et al., 1994;Yang and Torres-Verdín, 2011; Li et al., 2020).然而，兩類算法在尋優過程中皆要不斷調用正演，尤其對于三維地層環境而言，正演速度仍是制約反演效率的關鍵因素.

近年來，隨著智能算法的興起，有研究學者將深度學習技術引入地球物理反演當中(林年添等, 2018; Shahriari et al., 2020; Wu and Fan, 2021; Zhang et al.,2021)，以期能夠解決反演策略中正演效率低的難題.其中，反向傳播神經網絡(BPNN)作為一種強大的監督類學習架構，自從提出以來被廣泛用于特征識別以及函數逼近領域(Rumelhart and McClelland, 1986; Xu et al., 2018).然而，面對復雜輸入輸出問題，BPNN存在超參數優化困難、遷移性差、訓練參數過多以及不易收斂等缺點.為此，深層卷積神經網絡(CNN)憑借著局部連接和權重共享的優點逐漸代替BPNN(Fukushima, 1980; LeCun et al., 1998; Krizhevsky et al., 2017).在測井領域，Zhu等(2018)通過建立五層卷積神經網絡實現了地層巖性特征的快速識別；Li等(2019)基于1D模型和多層卷積神經網絡實現了大斜度井/水平井隨鉆電磁波測井的快速反演；Jin等(2019)通過優化卷積神經網絡的損失函數實現了隨鉆測井領域的實時地質導向.然而，上述研究皆是針對簡單輸入輸出問題，而對于陣列側向測井3D反演問題，國內外尚無研究.因此，針對陣列側向測井資料處理，如何提升高維正演效率，如何保證反演精度是當前智能測井領域亟需解決的難題.

為此，本文從三維有限元技術(3D-FEM)出發，首先對斜井各向異性地層參數進行敏感性分析，確定侵入、各向異性和地層傾角對陣列側向測井的敏感性大小；其次，建立三維陣列側向測井響應數據庫，引入二維卷積神經網絡(2D-CNN)技術，并基于二進制轉換將地層模型轉為網絡輸入層所需的2D圖像，提高網絡識別局部特征的能力；接著，建立深層2D-CNN結構，并引入“丟棄”(Dropout)和“填充”(Padding)機制，實現三維陣列側向快速正演；最后，基于敏感性分析和快速正演，將多種群遺傳算法與列文伯格馬奎特算法相結合(MPGA-LM)，對傾斜各向異性地層的電阻率剖面進行了快速精確重構.

1 陣列側向測井數值模擬

1.1 三維有限元數值模擬

本文以斯倫貝謝研發的高分辨率陣列側向測井儀HRLA為例，儀器包括一個主電極A0、六對屏蔽電極A1-A6(A1′-A6′)及兩對監督電極M1、M2(M1′、M2′)，屏蔽電極和監督電極關于主電極對稱，通過改變不同電極間的收發組合方式，可以形成6種具有不同探測深度的視電阻率曲線，探測深度由淺及深分別命名為RLA0，RLA1，RLA2，RLA3，RLA4，RLA5.

不同探測模式視電阻率可以通過測量監督電極電位進行計算，其中淺探測模式RLA0需要測量同側兩個監督電極的電勢差值ΔUM1M2(RLA0)，其他探測模式只需測量任意監督電極上電勢，其視電阻率計算公式如下：

(1)

(2)

式中，i為1～5，分別代表上述5種工作方式；Ki為第i種測井模式的電極系數，可在均勻地層條件下獲得；RRLAi為第i種測井模式的視電阻率；UM1(RLAi)為第i種測井模式的主電極電位；I0(RLAi)為第i種測井模式的主電極電流.

可以看出，求解陣列側向測井視電阻率的關鍵在于得到監督電極上的電勢，為此必須將整個空間的電位分布函數求出.由于陣列側向測井用的是低頻交流電，故可視為穩定電流，進而該問題轉為穩流場電勢分布函數的求解問題.

根據邊界條件和變分原理，陣列側向測井響應可歸結為求取泛函極值問題，泛函構造式如下：

(3)

式中，Λ為除去電極部分的求解區域，Ii和Ui分別代表儀器每個電極的電流和電勢大小.

在電阻率不同的子空間交界面上，電流、電位具有連續性，滿足如下邊界條件：

(4)

式中，“-”表示交界面左側(上側)，“+”表示交界面右側(下側)；n為交界面單位法向量.

在無窮遠邊界和絕緣電極表面還需滿足Dirichlet和Neumann邊界條件，如下所示：

U|Γ1=0,

(5)

式中，Γ1和Γ2分別為無窮遠邊界和絕緣電極表面.

在主電極和屏蔽電極表面，滿足等值面邊界條件：

(6)

式中，UAi為電極表面電勢，Γ3主電極或屏蔽電極表面，n為電極表面單位法向量，Ii為電極發射電流，i為0～5.

為求解上述泛函的最小值，一般采用三維有限元方法(3D-FEM)，最后采用前線解法求取含有大型稀疏矩陣的線性方程組，如式(7)，該方法由于可以在求解過程中對剛度矩陣邊消元邊安裝，可有效提升正演計算速度(張庚驥, 2009).

KΦ=F,

(7)

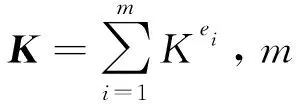
1.2 影響因素分析

陣列側向測井受泥漿侵入、地層傾角以及各向異性等多種因素影響，因此，確定各因素對測井響應影響強弱對于反演初值選取、約束條件施加具有重要意義.本節系統分析了侵入深度、各向異性和地層相對傾角等因素對陣列側向測井響應的敏感性，定義敏感因子S如下：

(8)

其中，i為陣列側向探測模式，此處取1～5，x為地層參數，分別代表侵入深度Di，各向異性系數λ和地層傾角θ.

首先，分析侵入對陣列側向測井響應的影響.以無限厚一層模型為例，地層為各向同性，侵入帶電阻率為2 Ωm，侵入深度Di變化范圍為0～3 m，侵入帶與原狀地層電阻率對比度范圍Rat為1～20.敏感性分布圖如圖1所示，橫縱坐標分別為侵入深度和電阻率對比度.可以看出，陣列側向測井對侵入深度敏感因子最大約為2，且隨著探測深度的增大，對侵入深度的敏感區間也隨之增大：淺、中、深探測模式RLA1、RLA3和RLA5的敏感區域分別為0.2～0.5 m、0.3～1.0 m和0.6～2.3 m.

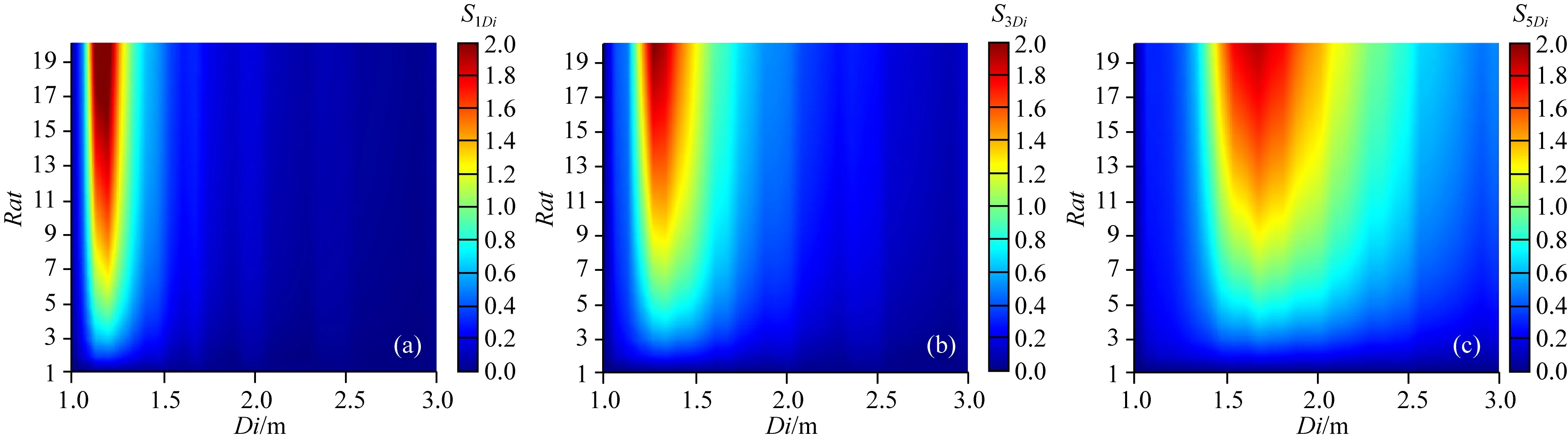
圖1 HRLA對侵入深度的敏感性 (a)?RLA1/?Di； (b)?RLA3/?Di； (c)?RLA5/?DiFig.1 The sensitivity of HRLA to invasion depth

接著，分析各向異性和地層傾角對陣列側向測井的影響.以無限厚模型為例，地層為各向異性，地層水平電阻率為2 Ωm，各向異性系數變化范圍為1～4，地層相對傾角變化范圍為0°～90°.圖2和圖3分別表示各向異性和地層相對傾角的敏感性分布圖，橫縱坐標分別為各向異性系數和地層相對傾角.可以看出：(1)陣列側向測井對各向異性系數和地層相對傾角的敏感因子最大約為1；(2)陣列側向測井在高角度地層(60°～90°)對各向異性最為敏感，且探測深度較深的測井模式對各向異性的敏感性較大，原因在于當地層相對傾角逐漸增大時，儀器電極發射電流方向逐漸朝著垂直電阻率方向傾斜.因此，垂直電阻率對測井響應貢獻變大，各向異性敏感性增強，而深探測曲線因探測范圍最廣，受其影響最大；(3)陣列側向測井在中高角度(50°～80°)對地層相對傾角最為敏感，且不同測井模式對相對傾角的敏感性與各向異性相似，皆是探測深度較深的測井模式對其敏感性較大，原因在于地層傾角對陣列側向曲線的影響本質是因為地層各向異性的影響，因為地層傾角增大，導致垂直電阻率的影響增大，進而使得陣列側向五條曲線出現變化.

圖2 HRLA對各向異性的敏感性 (a)?RLA1/? λ； (b)?RLA3/? λ； (c)?RLA5/? λ.Fig.2 The sensitivity of HRLA to anisotropy

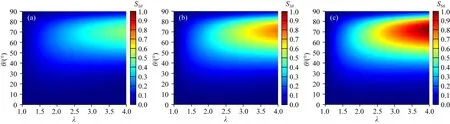
圖3 HRLA對地層相對傾角的敏感性 (a)?RLA1/? θ； (b)?RLA3/? θ； (c) ?RLA5/? θ.Fig.3 The sensitivity of HRLA to dipping angle

2 深層卷積神經網絡快速正演模型

2.1 深層卷積神經網絡理論

深層卷積神經網絡憑借著強大的泛化特性以及學習能力被廣泛用于圖像分類、語音檢測以及物體識別等復雜特征識別領域.一般而言，卷積神經網絡包括輸入層、卷積層、匯聚層(池化層)、全連接層和輸出層，本文以經典二維卷積神經網絡——LeNet-5為例，其結構如圖4所示.其中，輸入層為三通道RGB圖像或者單通道灰度圖像，卷積層包含多個卷積核，不同的卷積核相當于不同的特征提取器，結構為一個二維矩陣，圖像經過卷積層可提取多個局部特征并保存；匯聚層的作用在于特征選擇，降低特征數量，從而減少參數數量，其核心思想在于步長間隔的選擇，達到“降維”的作用；全連接層與全連接前饋神經網絡相同，不再贅述.

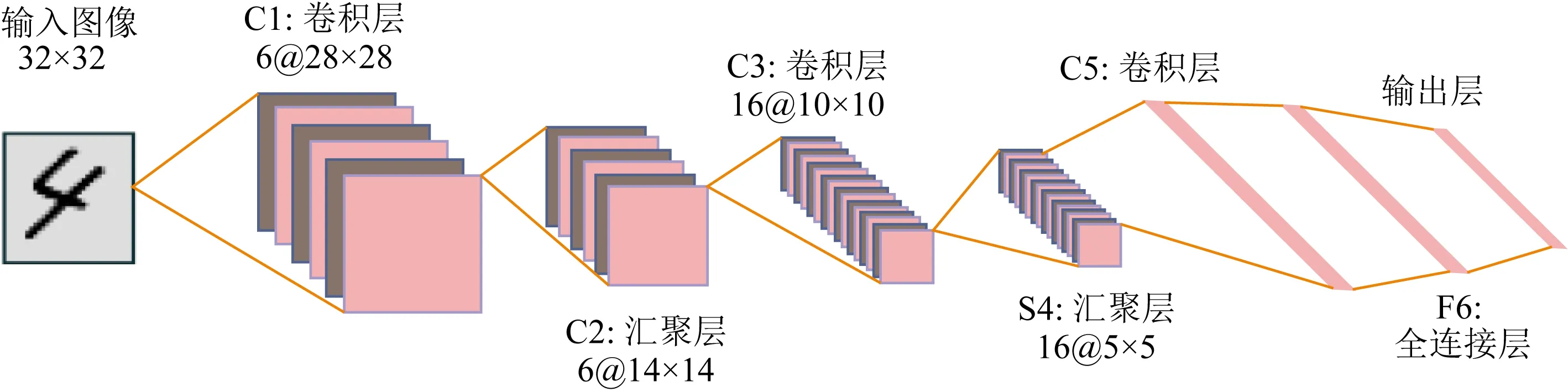
圖4 LeNet-5網絡結構Fig.4 The architecture of LeNet-5

相較于全連接神經網絡，卷積神經網絡最大的特點在于局部連接和權重共享，如圖5所示，圖5a為傳統的二層全連接神經網絡，包括3個輸入，5個輸出，需訓練參數包括15個權重和1個偏置共16個參數；圖5b為二層卷積神經網絡，包括3個輸入，5個輸出，由于輸入層每個神經元只需要與下層局部窗口內的神經元連接，且每個窗口內權重共享，若卷積核大小為3，則需訓練參數包括3個權重和1個偏置共4個參數，可大大減少訓練參數的數量，提高訓練效率.

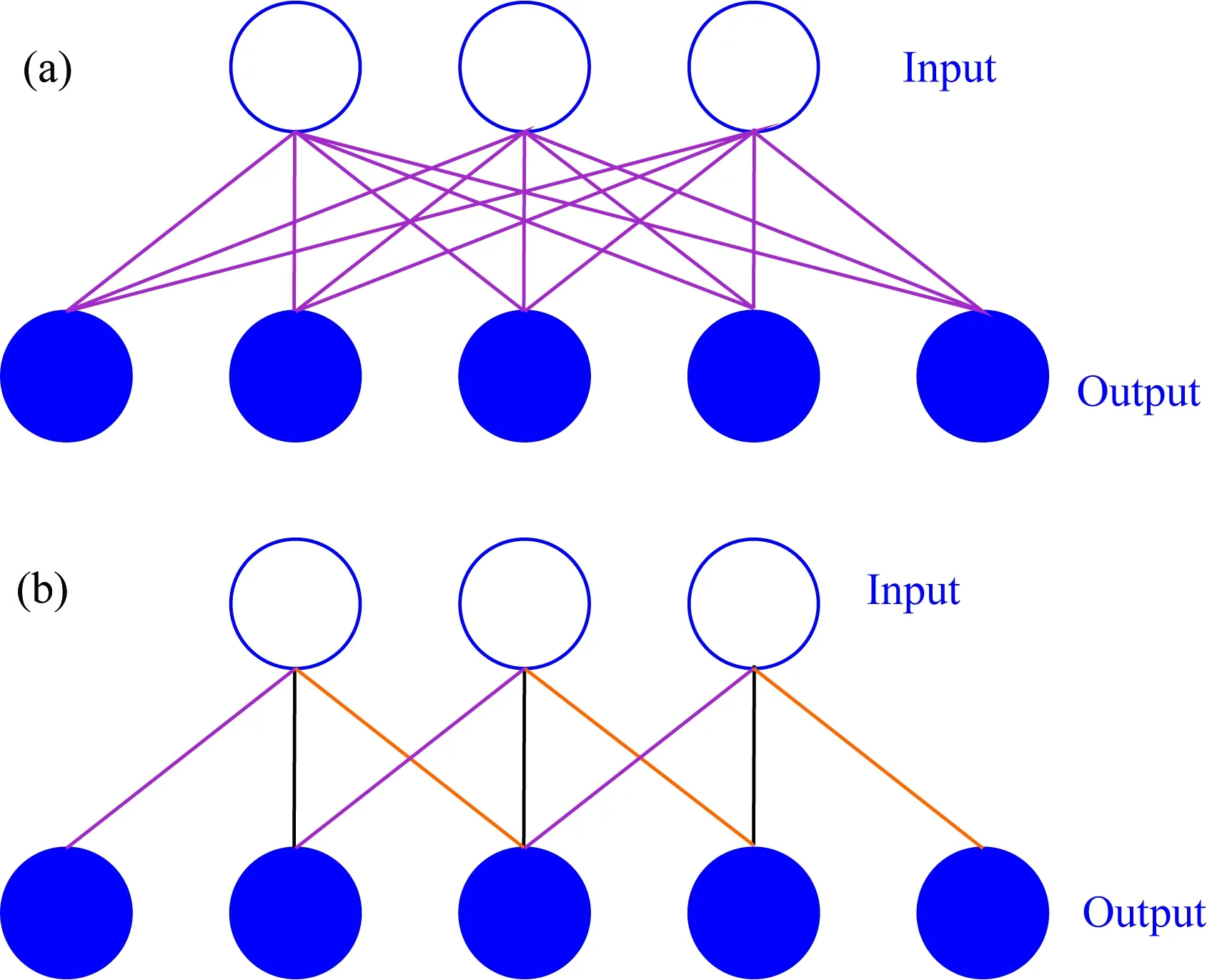
圖5 神經網絡結構 (a) 全連接層； (b) 卷積層.Fig.5 The connection feature of network (a) Fully connected layer； (b) Convolution layer.

同時，為提高深層神經網絡的訓練效率，通常卷積層和全連接層分別引入填充(Padding)和丟棄(Dropout)機制，如圖6所示，通過在圖像卷積之前填充一層像素，使卷積之后的圖片與原圖尺寸相同，進而使得卷積層得以加深，提高訓練精度，如圖6a；另外通過隨機丟棄部分神經元，可有效防止網絡過擬合，加快訓練進程，如圖6b.

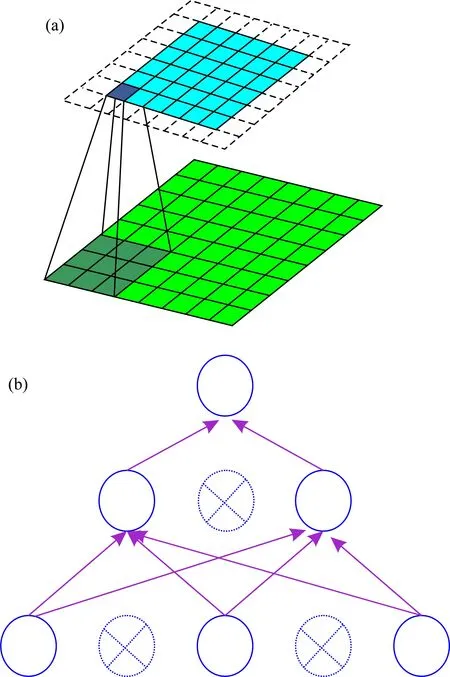
圖6 神經元連接機制 (a) “Padding”機制； (b) “Dropout”機制.Fig.6 Neuronal connection mechanism (a) “Padding” mechanism； (b) “Dropout” mechanism.

2.2 數據庫構建及模型可視化

神經網絡模型的可靠性和穩定性很大程度上依賴于訓練數據的精度，因此，本文基于嚴格三維有限元算法，構建大型數據集，并將其載入深層2D-CNN進行訓練，以此建立快速回歸模型.考慮圍巖和層厚對陣列側向測井響應的影響，數據集基于三層地層模型構建，如圖7a所示，該模型亦作為2D-CNN的輸入.具體地，令兩側圍巖為各向同性地層，電阻率相同，中間層為有侵各向異性地層，模型參數范圍如下：各向異性系數λ為1～4，分為13組，間隔0.25；侵入深度Di為0～1 m，分為11組，間隔0.1 m；圍巖電阻率Rs、沖洗帶水平電阻率Rxoh和目的層水平電阻率Rth范圍皆為0.1～500 Ωm，將其以對數形式各分為20組，對數間隔為0.19；兩側圍巖為半無限厚地層；目的層厚度H為0～5 m，分為16組，間隔0.33 m；測量點為以目的層中點為中心，上下各取兩個點，共5個測量點，采樣點間隔為0.1 m.需要注意的是，為簡化數據庫構建流程，將其按地層傾角分為10個子庫，每個子庫地層傾角間隔10°.因此，每個子庫有13×11×203×16，共18,304,000個樣本，每個樣本包括六個模型參數，共109,824,000個模型數據，將其儲存至變量M中，大小為18304000×6；同時每個樣本含有五個測量點，每個測量點包括五個電阻率值(RLA1～RLA5)，因此，每組共包含457,600,000個數據點，將數據點作為輸出儲存至變量D中，大小為18304000×25.在計算機內存中，每個數據點占8個字節，因此，每組數據大小約為0.944 GB，數據庫總大小為9.44 GB.

對于復雜模型回歸問題，1D-CNN訓練精度無法滿足需求，因此，本文采用學習和泛化能力較強的2D-CNN結構.而對于2D-CNN而言，輸入層普遍為2D圖像，為滿足網絡需求，本文基于二進制轉換將一系列一維模型數組轉化為二維字符串，進而合成一系列二值圖像(Zhong et al., 2019).具體轉換過程如圖7所示，其中圖7a為三層地層模型，具體模型參數如下：兩側圍巖為半無限厚各向同性地層，電阻率為2.564 Ωm，中間層層厚為3.156 m，侵入深度為0.428 m，侵入帶和目的層水平電阻率分別為11.278 Ωm和47.433 Ωm，各向異性系數為1.3，圖7b為模型參數對應的二進制矩陣，圖7c為基于二進制矩陣轉換為的二值圖像，每個模型可唯一對應一個二值圖像.由于數據庫中最大數值為8000，且小數后保留3位，故確定二進制字符串長度為32，若字符串長度過長，可自動補零.

圖7 模型可視化過程 (a) 地層模型； (b) 模型參數對應二進制矩陣； (c) 二值圖像.Fig.7 The process of model visualization (a) Formation model； (b) The binary matrix correspond to model parameters； (c) Binary image corresponding to formation model.

2.3 2D-CNN損失函數及數據歸一化

由于前饋神經網絡的局限性導致訓練精度偏低，為此本文將反向傳播技術應用于2D-CNN網絡架構中，定義損失函數如下：

(9)

g(w,b,x)=w?x+b,

(10)

σ(z)=max(z,0),

(11)

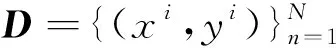
(12)

式中，L為神經網絡層數，Kl和Ml分別為第l層卷積核數量和卷積核尺寸.

接著，通過計算損失函數關于每層參數的梯度進行反向傳播，為不失一般性，本文使用鏈式求導法則對卷積層第l層的參數進行求導:

(13)

由式(10)和式(11)，易得

(14)

(15)

式中，k為第l層第k個特征映射，U為第l+1層的卷積核數量，X(l,k)=σ(g(l,k)).

同時，由于每組樣本中有5個測量點，即Y= (Y1，Y2，Y3，Y4，Y5)T，每個測量點包含五個視電阻率值，即Yi=(RLAi1,RLAi2,RLAi3,RLAi4,RLAi5)T.為提升訓練精度，可將數據進行歸一化處理，本文采用最小最大值歸一化方法，將輸出數據統一歸一化至[0,1]，公式如下：

(16)

需要注意的是，對于卷積神經網絡模型預測的數據而言，需將其反歸一化至正常值.

2.4 深層卷積神經網絡設計及測試

本文以9層卷積神經網絡為例，對大型數據集進行訓練測試，網絡結構及超參數定義如表1所示.網絡輸入為侵入深度、各向異性系數、侵入帶和原狀地層水平電阻率、圍巖層電阻率和目的層厚度所轉換為的二值圖像，即Input=BImage6×32×1, 輸出為陣列側向測井歸一化之后的視電阻率，即Output=RLA1×25.網格架構搭建平臺為：Pycharm2020.2.3，Python3.7和Tensorflow2.0(GPU版本).為防止訓練模型過擬合以及提升訓練精度，引入Dropout和Padding機制，其中Dropout率為0.5，Padding選擇‘same’模式，即每層輸入輸出維度一致，進而使得在每層輸入不丟失信息的前提下將卷積層延續，達到深化卷積層、提升訓練精度的目的.除此之外，由于匯聚層將卷積層提取的多個特征融合，而對于本文回歸問題，每個模型特征都是唯一的，因此，為保持模型特征完整性，不使用匯聚層.同時反向傳播算法采用自適應矩估計算法(Adam).訓練過程中，隨機選取95%的數據集為訓練集，剩余5%的數據為測試集.

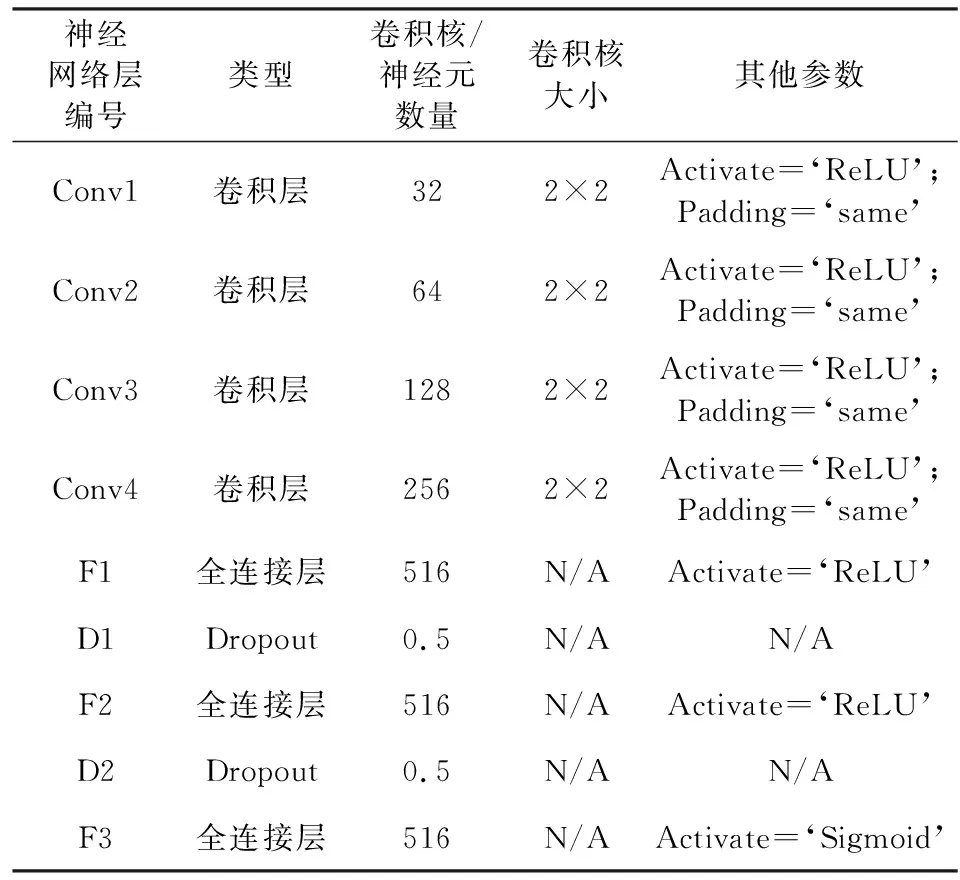
表1 2D-CNN超參數定義Table 1 The definition of hyperparameters in 2D-CNN

為測試2D-CNN網格訓練精度，本文將其訓練結果與BPNN對比分析，其中BPNN網絡架構與其類似，具體為：九層神經網絡結構，激活函數為ReLU，隱含層神經元個數分別為32，64，128，256，516，516，516，Dropout率為0.5，損失函數與反向傳播訓練算法與2D-CNN一致.圖8為其訓練精度與損失函數下降量的對比結果，綠色和黑色散點線分別代表2D-CNN和BPNN訓練結果，可以看出兩者收斂速度大致相同，但訓練精度卻相差較大，2D-CNN在100次迭代后訓練精度即可達到99%左右，而BPNN為85%.除此之外，BPNN容易陷入局部極小值，精度無法隨著迭代的進行而提升，相較而言，2D-CNN不僅可以快速收斂，而且訓練精度隨著迭代的進行逐漸接近100%.測試集與之規律類似，不再贅述.另外，通過計算2D-CNN和BPNN在測試集上的泛化誤差，計算公式如式(17).我們發現，兩者泛化誤差分別為1.28%和16.37%，從而也佐證了2D-CNN算法的高效性.

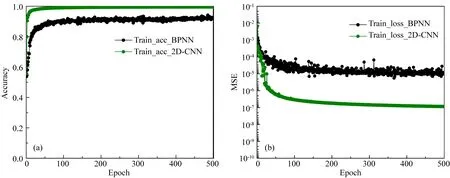
圖8 神經網絡訓練結果 (a) BPNN和2D-CNN預測精度； (b) BPNN和2D-CNN損失函數.Fig.8 Neural network training results (a) Prediction accuracy of BPNN and 2D-CNN； (b) Loss function of BPNN and 2D-CNN.

(17)

式中，ntest為測試集樣本數，此處為211200；RLAij_2D-CNN為2D-CNN計算結果，RLAij_3D-FEM為3D-FEM計算結果.

除此之外，為驗證訓練模型的精度，我們隨機選取20個樣本點，分別測試中間層原狀地層水平電阻率與各向異性系數對模型預測精度的影響，如圖9所示，實線代表3D-FEM計算結果，散點表示2D-CNN預測結果.樣本點模型皆為三層模型：Rs為2 Ωm，H為4 m，Di為0.5 m，Rxoh為20 Ωm.其中圖9aλ為1.5，Rth變化范圍為1～500 Ωm；圖9b中Rth為100 Ωm，λ變化范圍為1～3.從對比結果可以看出，兩者吻合度極高，最大相對誤差分別為0.81%和0.24%.因此，基于深層卷積網絡的快速正演模型滿足精度需求，為斜井各向異性地層的快速反演提供有力支撐.

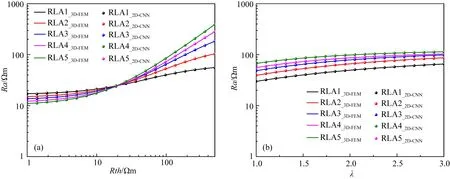
圖9 2D-CNN精度測試 (a) Rth對預測精度的影響； (b) λ對預測精度的影響.Fig.9 Prediction accuracy testing of 2D-CNN (a) The effect of Rth on the prediction accuracy； (b) The effect of λ on the prediction accuracy.

3 混合MPGA-LM算法及快速反演流程

3.1 代價函數定義

大斜度井/水平井陣列側向測井是典型的非線性反演問題，確定性算法L-M算法由于結合高斯牛頓算法和最速下降法的特性，能夠彌補全局尋優能力不強或收斂性差的缺陷，反演過程中采用的代價函數如下：

(18)

式中，x為待反演參數矢量，x=(Di,Rxoh,Rth,λ,Rs)T，上標T表示矩陣的轉置，S(x)為陣列側向儀器正演響應，dobs為實際測量數據，‖·‖2表征L2范數，xp為模型已知參考矢量，通常是上一步迭代參數矢量，ξ為正則化參數，最后一項的作用是壓制測量噪聲，同時減小非線性反演出現的病態問題.反演的目的是得到一個x*使得代價函數最小，即x*=argmin{C(x)}.

進一步，經二階泰勒近似，可得第k步迭代步長xk為

xk=-JT(xk){S(xk)-dobs)}[JT(xk)J(xk)+ξkI]-1,

(19)

式中，I為單位矩陣，J為S在xk處的雅克比矩陣，ξk為第k次迭代的正則化參數大小.

為克服傳統差分方法計算雅可比矩陣耗時的缺陷，本文采用Broyden近似方法進行雅可比矩陣的迭代更新(Broyden, 2000).

·(xk)T,

(20)

式中，J(xk+1)為第k+1步的雅可比矩陣.

3.2 基于MPGA的初值優選策略

由于L-M算法對初值依賴性較強，若初值選取不適，算法易困于局部極小值，反演精度低.為此，本文基于卷積神經網絡快速正演模型，同時為克服標準遺傳算法(GA)早熟早收斂的缺陷，利用多種群遺傳算法(MPGA)優化初值選取，進而提升L-M算法全局尋優能力.

如圖10所示，多種群遺傳算法的核心在于將多個種群進行初始化，即“二進制”編碼，并同時進行選擇、交叉和變異操作.種群間通過移民算子進行協同進化，最后通過適應度函數分析，借助人工選擇算子選取種群最優個體組成精華種群.本文定義適應度函數如下：

圖10 多種群遺傳算法流程Fig.10 The framework of multi-population genetic algorithm

(21)

式中，p= 1,2,…,P，P為種群數量，n=1,2,…,N，N為每個種群個體數量，m為每個測量點數據量，此處為25.

除此之外，本文所采用的多種群遺傳算法超參數選擇如下：種群數目為5，個體數目為30，最大遺傳代數為50，變量的二進制位數為32，交叉概率在[0.7，0.9]內隨機產生，變異概率在[0.001，0.05]內隨機產生.

為測試初值選取精度，以30°三層地層模型為例，兩側為各向同性圍巖，中間層為有侵各向異性地層.表2為測試模型參數分布以及多種群遺傳算法初值選取結果，Mode l1-Mode l5層厚分別為1～5 m，間隔為1 m.可以看出，受層厚影響，當層厚小于3 m時，圍巖電阻率可準確選取，平均相對誤差為4.4%；當層厚大于3 m時，陣列側向測井響應基本不反映圍巖信息，選取誤差急劇增大，而此時其他參數選取較為精確，整體而言，侵入深度平均相對誤差為18.6%，各向異性系數為17.8%，侵入帶和原狀地層水平電阻率分別為18.7%和6.8%，選取精度滿足L-M算法需求.

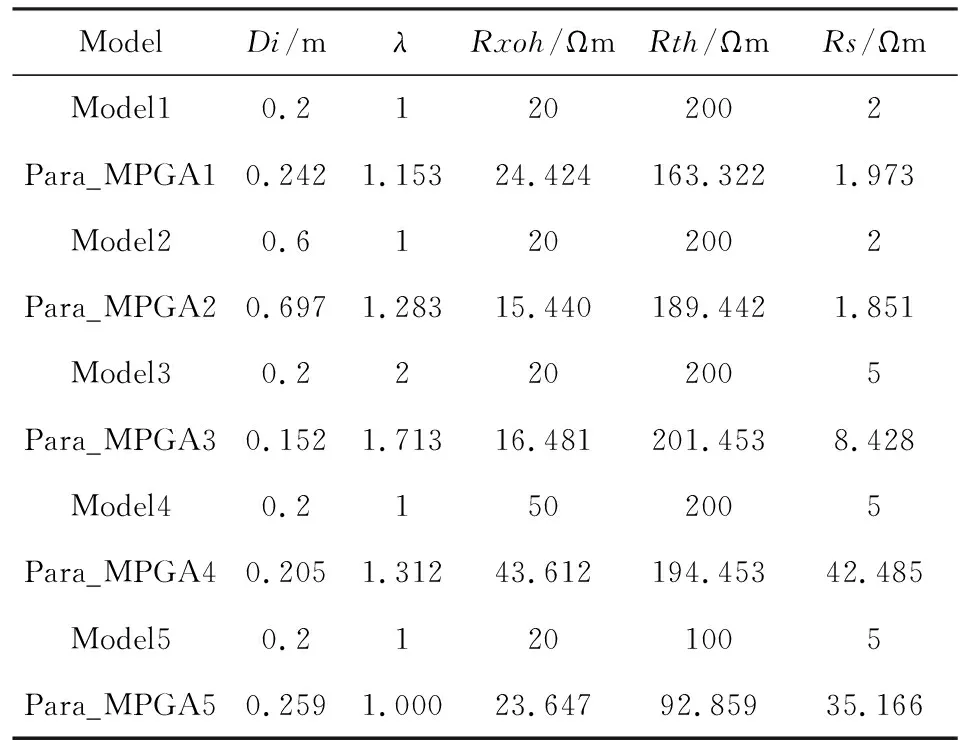
表2 初值選取結果Table 2 The selection result of initial value

3.3 混合MPGA-LM快速反演流程及有效性測試

實際資料處理過程中，針對帶有深度點的大型測井響應數據集，我們將其由上到下分為若干子區域，每個子區域為三層模型，中間層為有限厚，地層厚度由層界面位置決定，而層界面位置可通過視電阻率曲線拐點或伽馬、自然電位等巖性曲線確定，上下地層視為無限厚地層進行處理.圖11為混合MPGA-LM反演流程圖，由上節可知，經MPGA優選后的參數分布于反演代價函數真實解附近，故可將其作為L-M算法的初值，進而提升反演效率；另一方面，由于當層厚大于3 m時候，圍巖對陣列側向響應近乎無影響，此時反演參數可降為4個，即Di、Rxoh、Rth和λ.同時，為提高訓練精度，反演可循環N次(本文N為2)，即處理完整個井段資料后，可進行二次處理.

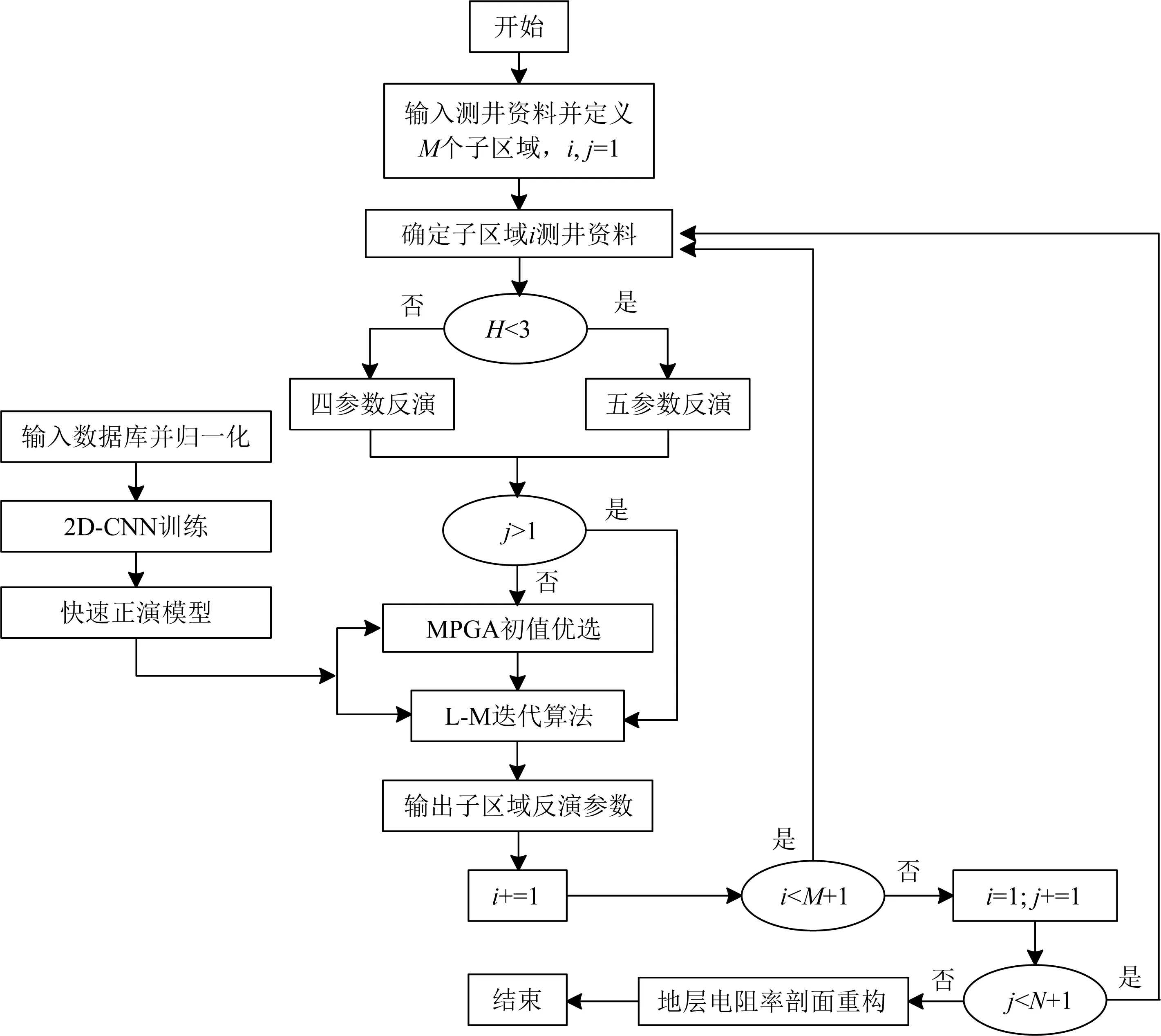
圖11 混合MPGA-LM反演流程Fig.11 The workflow of hybrid MPGA-LM scheme

另外，為測試混合MPGA-LM快速反演算法的有效性，本文以三層模型為例，分別采用簡單初始模型與MPGA提供的初始模型進行反演對比，反演算法皆為LM算法.地層傾角選擇30°，模型參數分布如表3所示.其中，在簡單初始模型中分別將深、淺測井響應RLA1和RLA5作為Rxoh和Rth的初始值，Di和λ的初始值分別為0.5 m和1.5，表3為兩者方法反演結果及相對誤差，可以看出，較之簡單初始模型的LM算法，MPGA-LM可以更好的將地層剖面重構，反演精度更高.以中間地層反演結果為例，基于簡單初始模型的LM算法反演后Di、λ、Rxoh和Rth的相對誤差(RE)分別為36.67%、33%、84.10%和23.08%；MPGA-LM反演后Di、λ、Rxoh和Rth的相對誤差分別為3.33%、0.50%、6.40%和2.86%，精度可以提高數倍至數十倍，由此本文提出的混合MPGA-LM快速反演算法的有效性得到了驗證，為下文數值模擬實例的分析提供了保障.

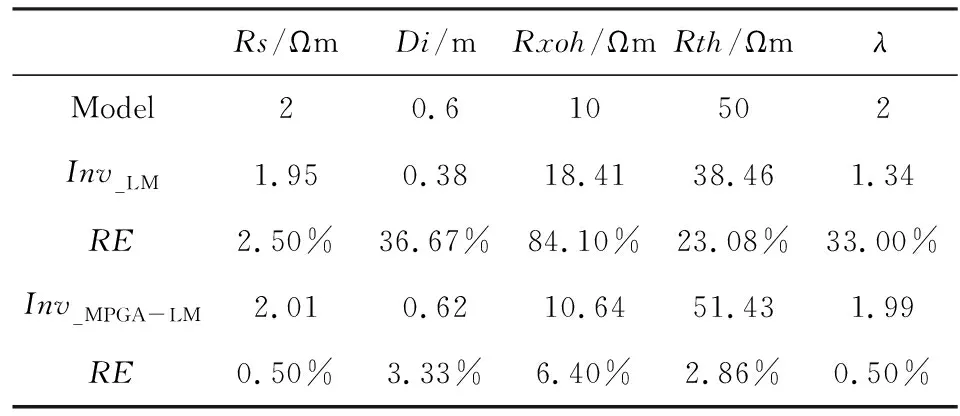
表3 LM與MPGA-LM算法反演結果對比Table 3 The inverted results comparison between LM and MPGA-LM algorithm

4 數值模擬實例

本節通過建立21層俄克拉荷馬模型，進一步驗證上述反演方案的有效性.模型參數如下：井徑為8 inch，泥漿電阻率為0.1 Ωm，地層相對傾角分別

為0°、30°和60°，侵入深度范圍0～1.0 m，侵入帶水平電阻率分布范圍為0.2～30 Ωm，原狀地層水平電阻率范圍為0.2～100 Ωm，各向異性系數范圍為1～2.5 Ωm.圖12為該模型參數分布示意圖，縱坐標為真實垂直深度(TVD).圖13為地層相對傾角分別為0°、30°和60°時陣列側向測井響應.本文將地層界面位置作為已知條件，僅反演侵入深度、侵入帶電阻率以及原狀地層電阻率.

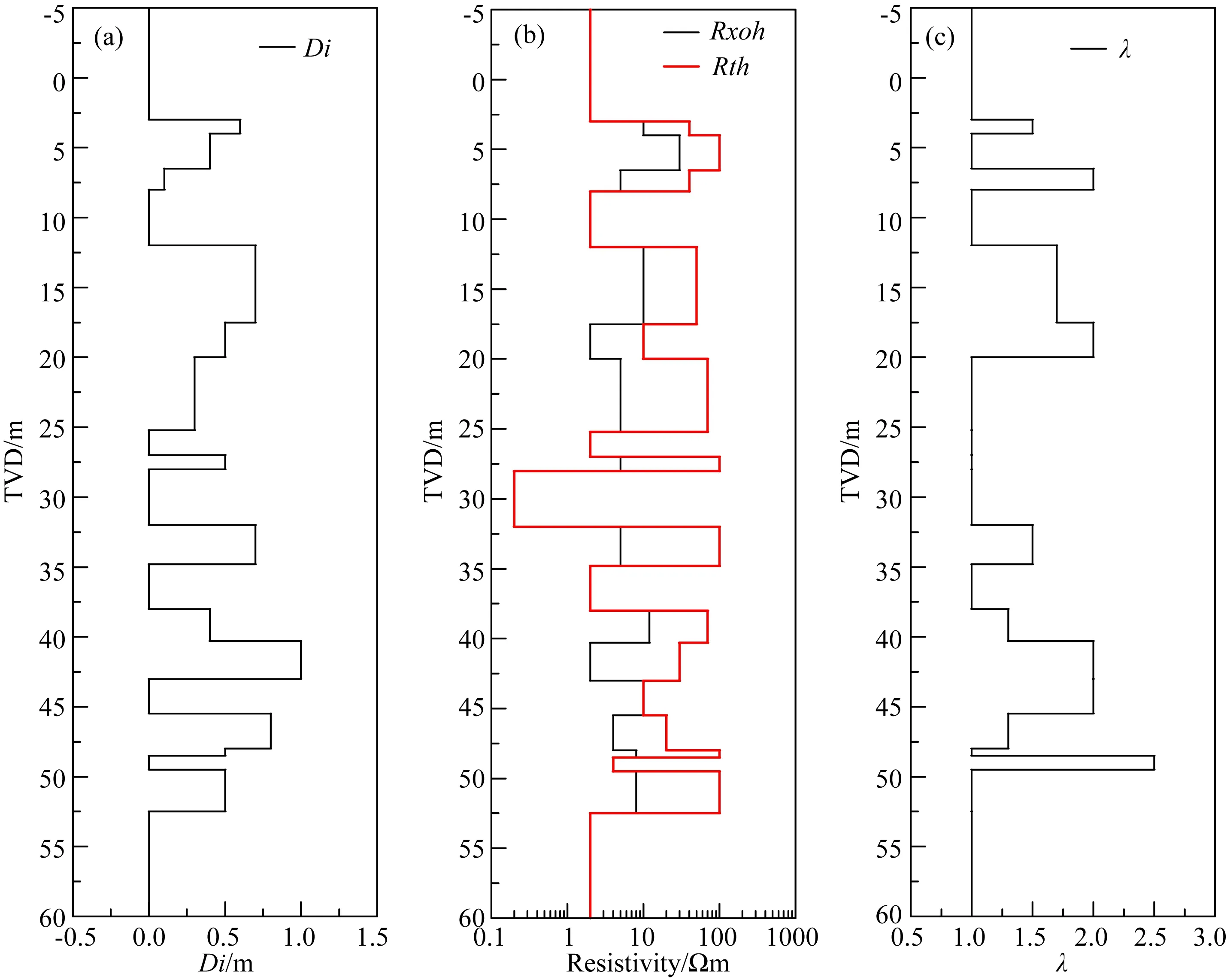
圖12 俄克拉荷馬模型參數分布 (a) 侵入深度； (b) 侵入帶和原狀地層水平電阻率； (c) 各向異性系數.Fig.12 The Oklahoma model parameters (a) Di； (b) Rxoh and Rth；(c) λ.

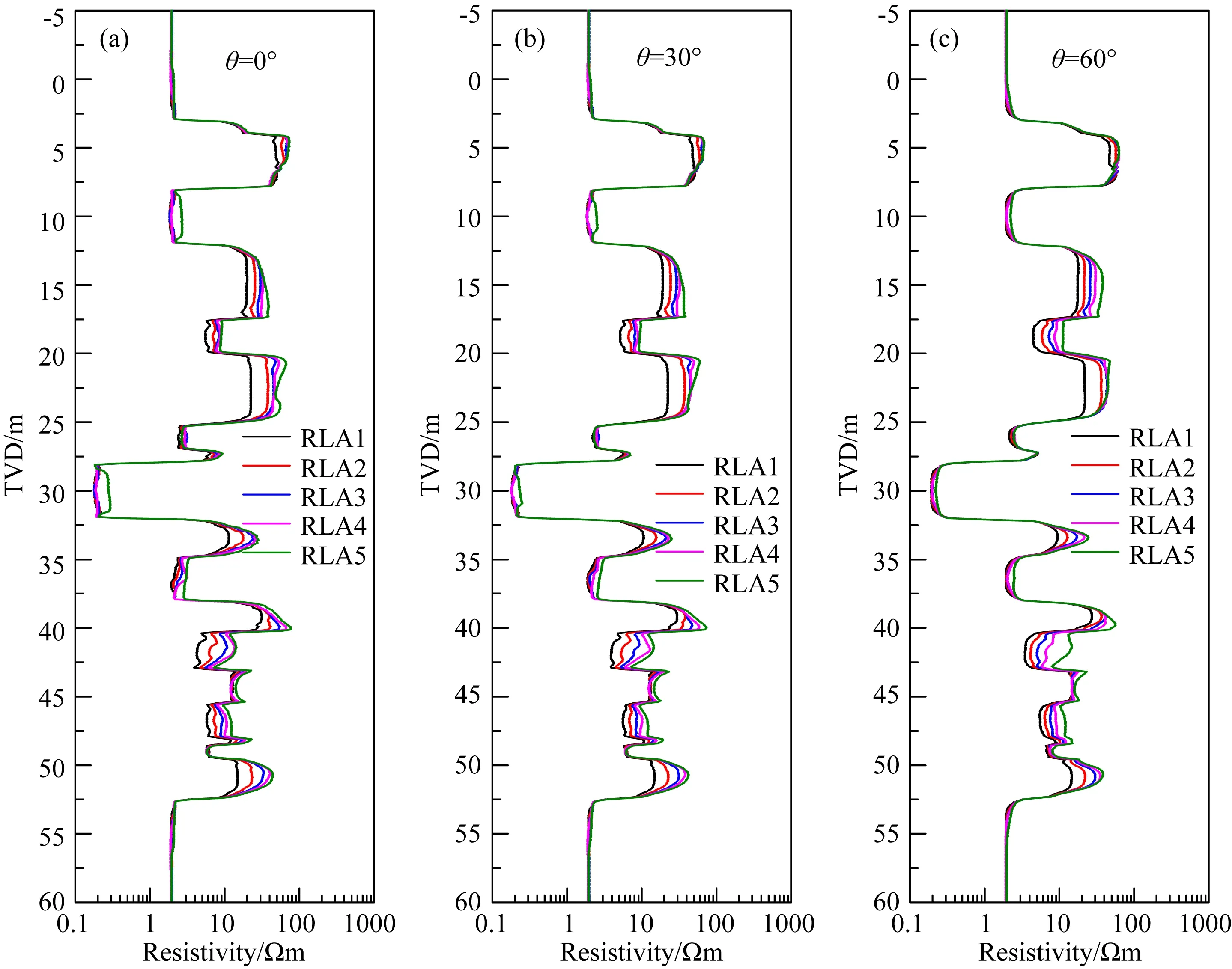
圖13 陣列側向測井響應結果 (a) 0°； (b) 30°； (c) 60°.Fig.13 The responses of array laterolog

從測井響應結果可以看出，泥漿濾液侵入對其影響嚴重，如模型第八層，該層為各向同性地層，厚度為5.2 m，侵入深度為0.3 m，地層真實電阻率為70 Ωm，而視電阻率值在0°、30°和60°時與地層電阻率的最大偏離度，即max(RLA/Rth)，分別為32.16%、31.81%和31.03%，遠遠偏離地層真實電阻率；除此之外，由于受地層各向異性的影響，導致響應結果介于水平和垂直電阻率之間，如模型第16層，該層無侵入，地層水平和垂直電阻率分別為5 Ωm和20 Ωm，測井響應在0°、30°和60°時的視電阻率大小分別在12 Ωm、13 Ωm 和15 Ωm附近，可以看出，60°地層對各向異性更為敏感，由此驗證了2.3部分的結論.由上述可知，單單從測井曲線無法提取地層真實電阻率，因此需借助反演手段對地層真實電阻率剖面進行重構.本文基于運行內存為8 GB 的英特爾i7-9700 處理器對60 m測井數據進行反演處理，數據采樣間隔為0.1 m，循環反演次數為2次，反演總耗時約6.8 min.圖14是基于本文提出的反演策略對測井資料處理后的結果.

從圖14反演結果及圖15反演誤差曲線可以看出，就反演精度而言，地層水平電阻率>侵入深度>各向異性系數，三者的相對誤差范圍分別為0～8.38%、0.11%～6.98%和0～14.35%，該現象可由1.3節結論解釋，即測井響應對侵入深度的敏感性大于地層各向異性；另一方面，地層傾角對侵入深度和地層水平電阻率的反演精度影響較小，而對地層各向異性影響較大，可以看出，三個角度下各向異性的反演相對誤差最大值分別為14.35%、7.79%和3.85%，該現象亦可由1.3節結論解釋，即高角度條件下陣列側向測井響應對各向異性的敏感性較強.

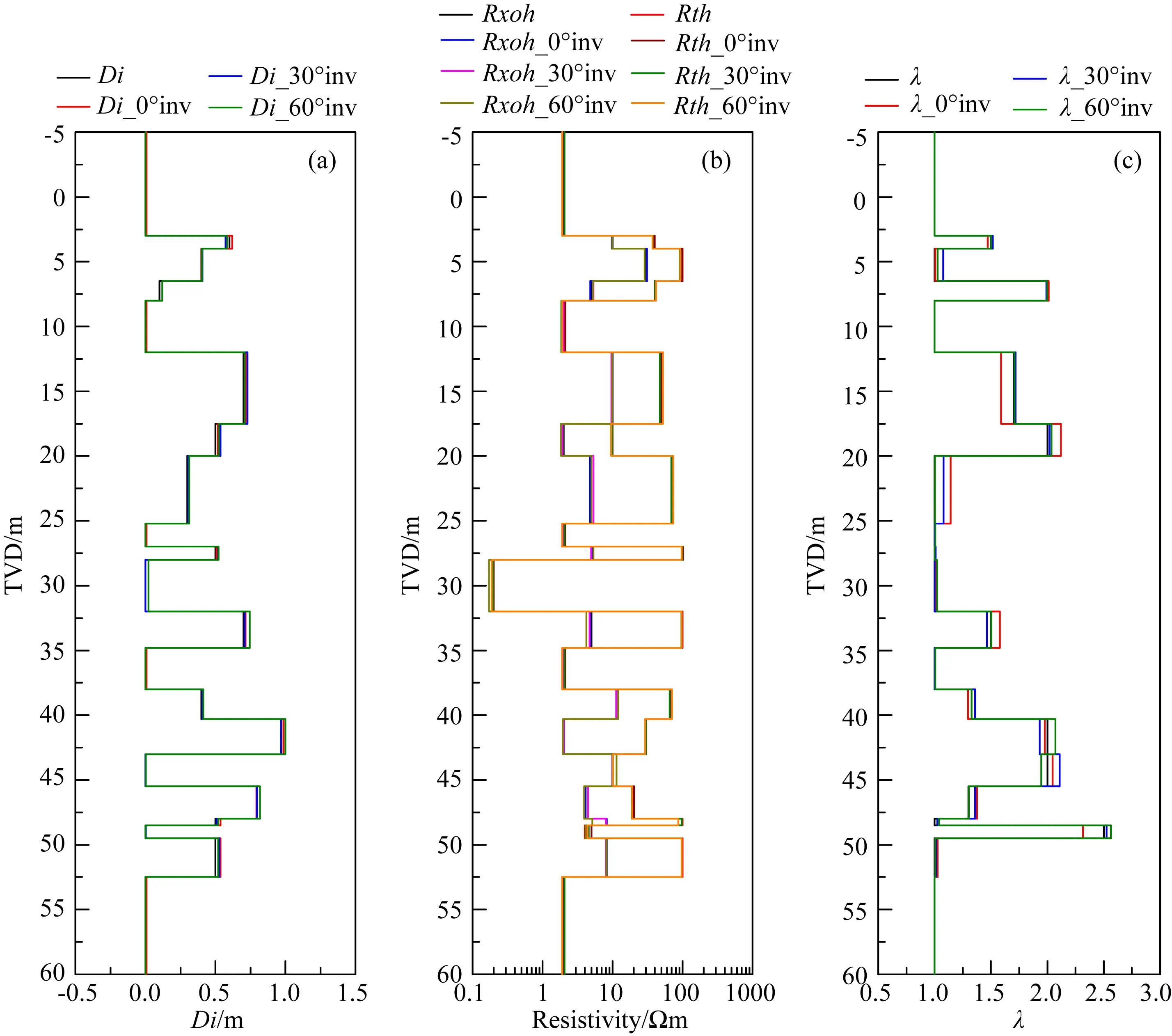
圖14 混合MPGA-LM反演結果 (a) 侵入深度； (b) 侵入帶和原狀地層水平電阻率； (c) 各向異性系數.Fig.14 The inverted results using hybrid MPGA-LM algorithm (a) Di； (b) Rxoh and Rth； (c) λ.

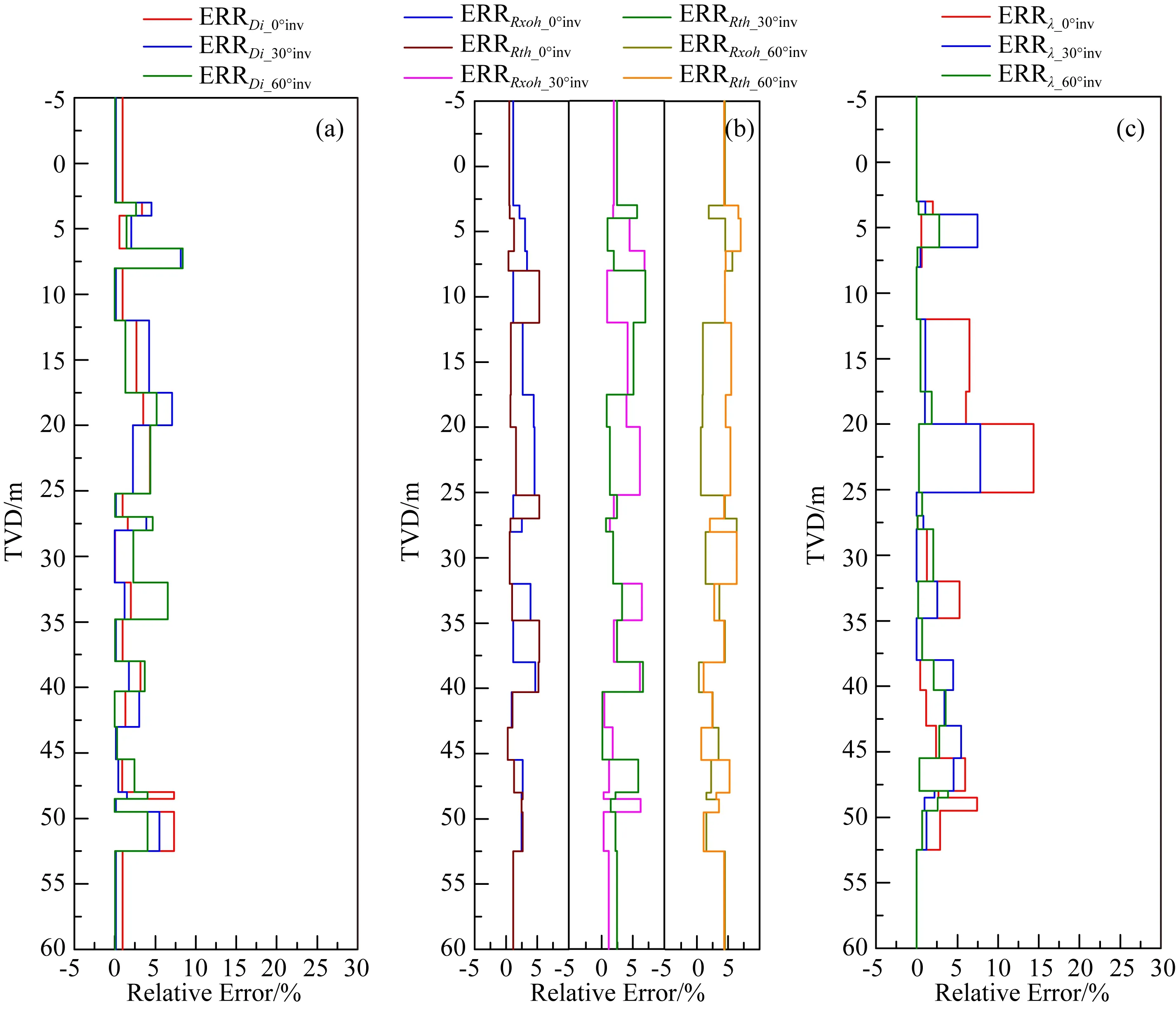
圖15 反演結果相對誤差 (a) 侵入深度反演誤差； (b) 侵入帶和原狀地層水平電阻率反演誤差； (c) 各向異性系數反演誤差.Fig.15 The relative error of inverted results (a) The relative error of inverted Di； (b) The relative error of inverted Rxoh and Rth； (c) The relative error of inverted λ.

另外，由于在反演過程中調用的正演模型是2D-CNN快速計算模型，而非3D-FEM算法，而2D-CNN模型缺乏對各向異性圍巖層的考慮.因此，為進一步分析反演誤差產生原因，我們將2D-CNN與3D-CNN的計算結果進行誤差分析，平均相對誤差(MRE)計算公式如式(22)所示，具體結果如表4所示.

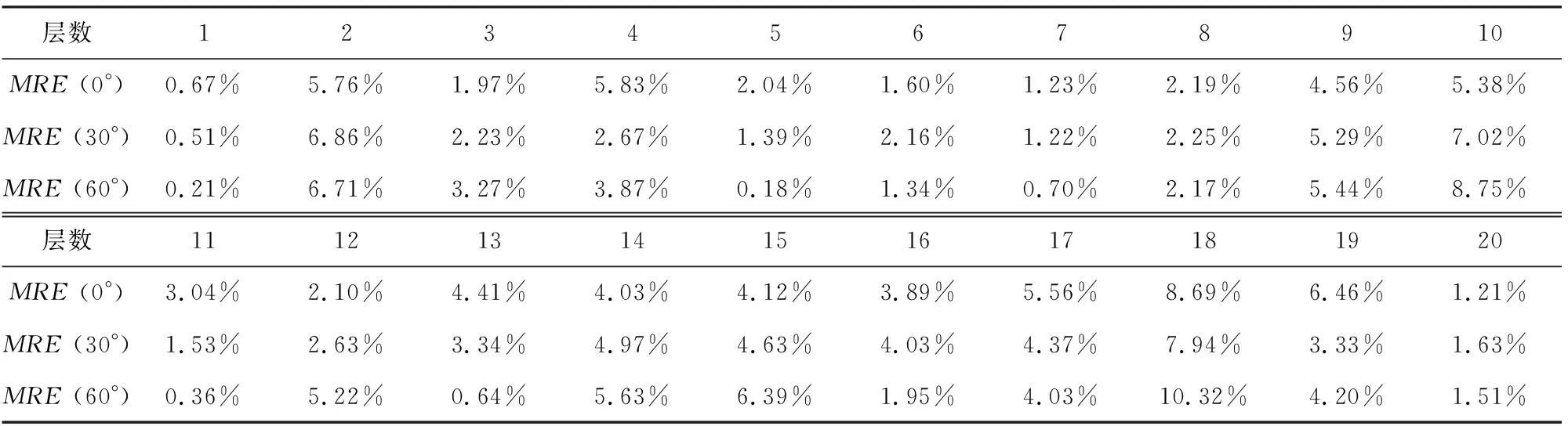
表4 2D-CNN與3D-FEM計算結果平均相對誤差Table 4 The mean relative error between the responses calculated by 2D-CNN and 3D-FEM

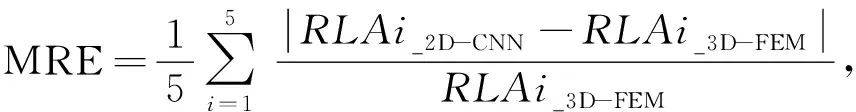
(22)

式中，RLAi_2D-CNN為2D-CNN計算結果，RLAi_3D-FEM為3D-FEM計算結果.

可以發現，整體而言，兩者平均相對誤差小于10%，對于大多數層而言，相對誤差小于3%，滿足精度要求.然而在薄層處，由于受到圍巖層厚、侵入和各向異性的影響，平均相對誤差普遍大于5%，如第2層、第10層和第18層等.該現象正是造成反演結果精度較低的原因之一.為此，在后續研究中，我們將繼續完善訓練模型，提升神經網絡算法對圍巖層特征的拾取能力.

值得注意的是，本文所采用的反演模型均為侵入模型，由于多解性問題的存在，會使得無侵地層的侵入深度反演結果不為0，但侵入帶電阻率和原狀地層電阻率的反演結果一致性較高，如模型第五層和第九層.整體而言，該方案可有效提升算法克服反演多解性的能力，進而提高傾斜各向異性地層陣列側向測井反演精度，給陣列側向測井實際資料處理提供一種新思路.

5 結論

針對傾斜各向異性地層，本文基于3D-FEM，分析了侵入深度、各向異性以及地層傾角等因素對陣列側向測井響應的影響；接著，引入2D-CNN網絡架構，針對侵入深度小于1.0 m，各向異性系數小于4，層厚小于5 m，圍巖和地層水平電阻率位于0.1～500 Ωm的地層，通過建立大型數據集以及將模型可視化，使得2D-CNN訓練精度和計算速度能夠滿足正反演需求，訓練精度達到99%左右，計算一個測井點僅需0.36 ms；在此基礎上，通過引入全局尋優能力較強的MPGA算法，可為L-M反演算法提供較為精確的初值，進而基于區域分解技術使得斜井各向異性地層電阻率反演精度達到90%以上.

不可否認的是，在更為復雜的三維地層條件下，例如碳酸鹽巖地層，存在裂縫和溶洞發育、地層各向異性強以及電阻率大等特征，本文提供的數據庫及網絡架構將不再適用，讀者僅需將其進行擴充與完善即可.另外，復雜三維地層的測井響應會使得反演多解性更為強烈，為此，在今后研究中，應進一步豐富和完善神經網絡架構以及反演方案，以期為油氣田開發提供更為便捷可靠的處理方案.