基于代理模型的噴水推進泵水力特性分析及優化

陳 杰，張孟杰，劉濤濤，*，吳 欽，葉哲豪

（1.北京理工大學 機械與車輛學院，北京 100081；2.中國北方車輛研究所，北京 100072）

0 引言

噴水推進作為一種特殊的推進方式[1]，相比于傳統的螺旋槳推進，噴水推進泵具有結構緊湊、效率高及附體阻力小等優點，逐漸成為兩棲車及船舶的主要推進方式[2-3]。

然而，兩棲車及船舶在啟航、加速以及轉彎等狀態時，噴水推進泵很容易進入空化工作區，空化的發生將直接導致噴水推進泵性能下降[4-5]。針對噴水推進泵的空化問題主要通過結構優化設計進行解決[6-8]，主要集中在試驗優化設計[9]、速度系數法優化設計[10]、損失極值法優化設計[11]、計算流體力學（CFD）優化設計[12]以及多工況優化設計[13]等方面。但噴水推進泵結構往往較為復雜，工作環境惡劣，傳統的優化方法都具有一定的局限性，或需要大量準確的公式推導，或有賴于設計者的經驗和試驗結果借助仿真軟件進行多次重復建模才能得到設計目標的變化趨勢。

近年來由Shyy等[14]提出的代理模型優化設計方法有效避免了傳統優化方法的不足，可有效過濾數值仿真或者實驗結果中的噪聲，最大程度上保證設計結果的準確性，同時還可得到多目標的優化結果。Goel等[15]采用代理模型的方法對泵的葉片幾何形狀進行了優化，取得了理想的結果。趙宇等[16]以泵首、次級葉輪的葉片安放角以及相位角作為優化設計參數，以效率和壓力系數為優化目標，采用代理模型的方法對某一串列泵進行優化設計，使得泵效率和空化性能均有所提升。吳欽等[17]利用代理模型分析方法對考慮了模型參數和物質屬性的 Merkle空化模型在低溫介質空化流動計算中的應用進行了評價和優化，提高了模型的預測能力。熊英華等[18]以誘導輪出口安放角和泵葉輪進口安放角為優化參數，泵揚程系數和空化余量為優化目標，采用代理模型的方法對某航空燃油泵進行優化設計，結果顯示，優化后的燃油泵空化性能提高了18%。谷海濤等[19]以某種水下滑翔機為研究對象，構建機翼的代理模型優化設計方法，優化結果顯示，滑翔機的運動性能提高，升阻比較之前提高了6.76%。Fan等[20]采用移動最小二乘法建立代理模型，對射流泵為研究對象進行全局優化，在泵輸入功率減小20%的同時，效率提高4%。

本文采用代理模型優化方法對設計工況下的噴水推進泵結構參數進行優化分析，基于全局敏感度分析方法評價了葉輪葉片進出口安放角對噴水推進泵水力特性的影響，同時采用數值計算方法對優化后的噴水推進泵性能進行了分析。

1 數值計算方法

1.1 基本控制方程

研究采用均質平衡流模型，假設汽液兩相為均相流動，相間無相對速度，考慮汽液兩相間的傳輸速率，則基于Favre平均的Navier-Stokes方程為

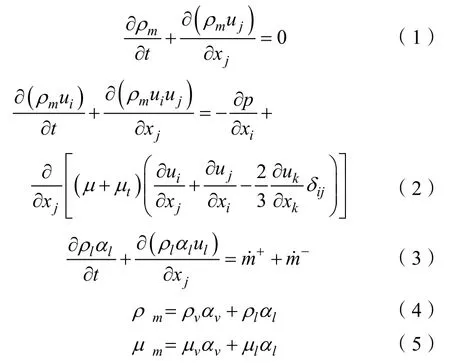
1.2 基于標準SST k-ω模型的旋轉修正湍流模型

由Menter提出的SST k-ω湍流模型[21]如下：

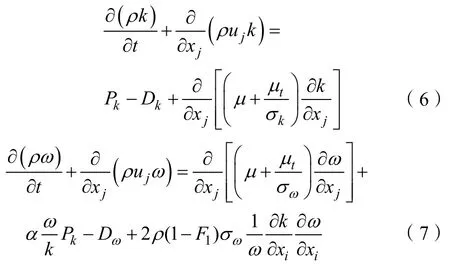
湍流粘性系數由下式確定：

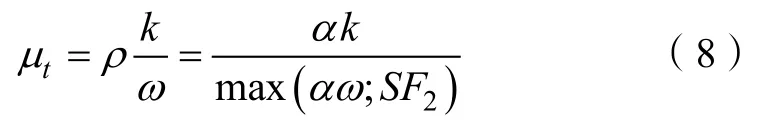
式中：Pk為湍流生成項；Dk、Dω為湍流耗散項；F1、F2為混合函數；S為剪應力張量的常數項。

由于葉輪的高速旋轉，推進泵內部流場具有強烈的旋轉曲率效應，標準的SST k-ω渦粘模型難以捕捉強旋轉和大曲率流動。為了解決這一問題，本文研究中基于局部渦旋運動效應對標準SST k-ω湍流模型k方程和ω方程中的Pk進行修正，旋轉修正函數為

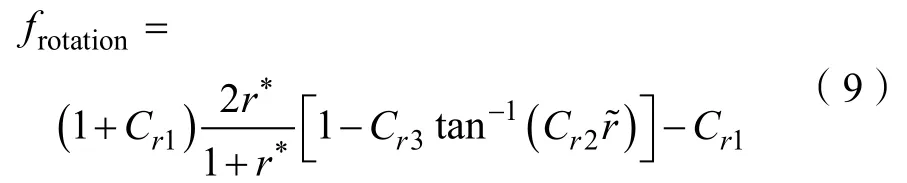
式中：r*和分別為當地渦旋運動引起的流線曲率和流場旋轉效應；經驗常數 Cr1=1.0，Cr2=2.0，Cr3=1.0。

考慮到數值計算穩定性的要求，計算中對旋轉函數做如下限定：

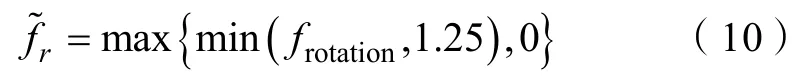
則修正系數fr為

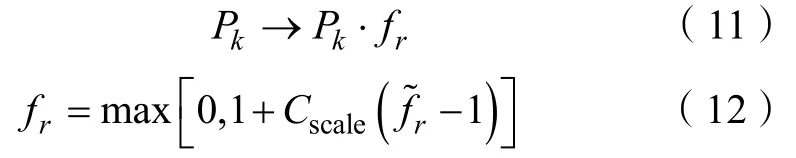
式中，Cscale為比例系數，默認值為1。

1.3 空化模型

計算采用基于 Rayleigh-Plesset空泡生長方程得到的Zwart空化模型[22]，則蒸發和凝結項為

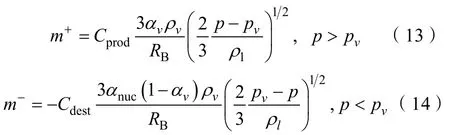
式中：αnuc=5×10-4為空化核子體積分數；RB=1×10-6m為空泡半徑；p和pv分別為當地壓力和汽化壓強；Cprod=0.01和Cdest=50分別為凝結和蒸發系數。

1.4 網格劃分與邊界條件設置

數值計算采用的軸流式噴水推進泵水力模型如圖1所示，其主要的幾何尺寸如表1所示，葉輪直徑D=300 mm，設計轉速 n=2 000 r/min，設計流量Qd*=0.802 m3/s，本文計算中流量范圍為設定為0.85～1.1 Qd*。

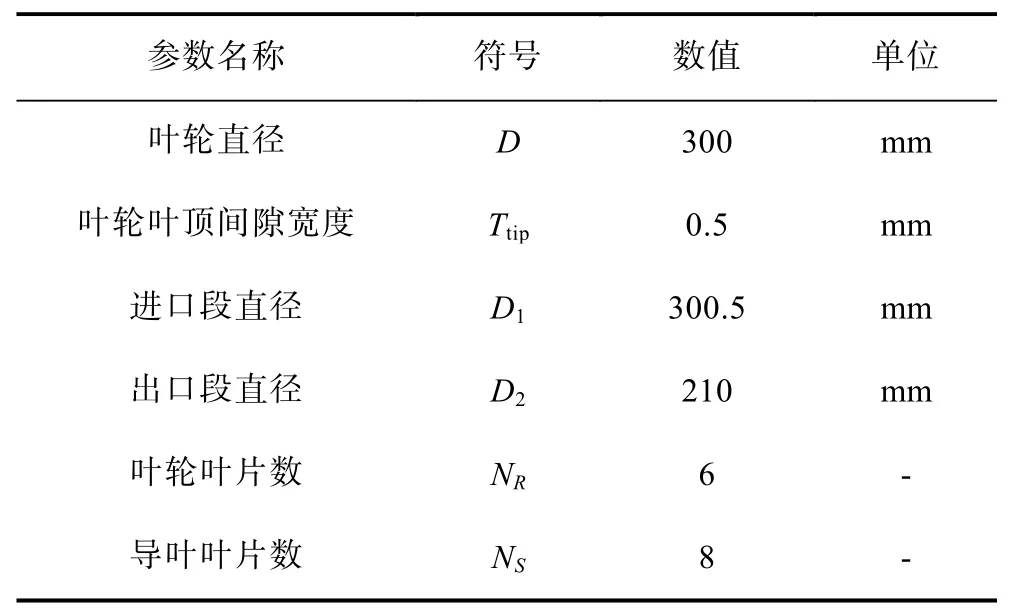
表1 軸流式噴水推進泵主要參數Table 1 Main parameters of axial flow water-jet propulsion pump

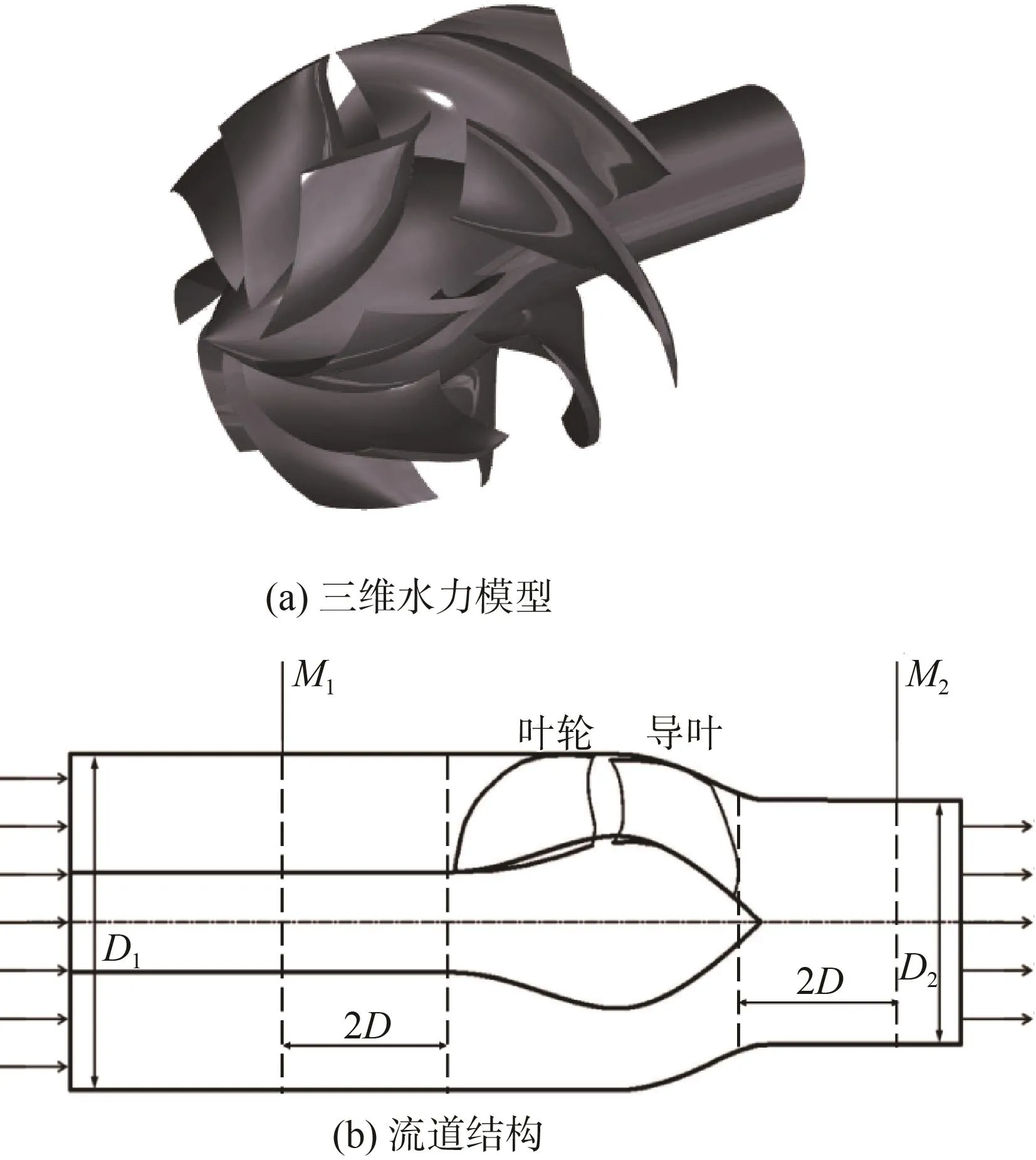
圖1 軸流式噴水推進泵水力模型及流道結構Fig.1 Hydraulic model and channel structure of axial flow water-jet propulsion pump

噴水推進泵采用六面體全結構化網格，其中進口段與出口段在ANSYS-ICEM中進行劃分，葉輪和導葉區域在 ANSYS-TurboGrid中進行劃分，近壁面區域采用分層網格局部加密處理，網格質量均在0.7以上，如圖2所示。計算采用總壓入口、質量流量出口邊界，葉片及輪緣輪轂均采用無滑移壁面邊界，壁面函數為標準壁面函數，動、靜交接面采用Frozen Rotor類型，以單相計算結果作為初值，進行迭代計算空化流動。

圖2 局部網格劃分示意圖Fig.2 Schematic diagram of local grid division

1.5 網格無關性及數值計算方法驗證

為了對網格無關性進行驗證，在相同計算條件下分別取網格數為320 W、360 W、400 W、440 W的網格進行計算。由于進、出口網格對整體性能影響較小，且在壁面處已進行加密處理，網格質量較高，計算中保持進、出口網格數量不變，只考慮葉輪和導葉的網格數量對外特性計算結果的影響，各流域的網格劃分如表2所示。圖3給出了在設計工況下（n=2 000 r/min，Qd*=0.802 m3/s）噴水推進泵外特性參數與網格數之間的關系，可以看出：隨網格數的增加，推進泵效率變化范圍較小；揚程系數和軸功率系數在網格數為400 W后基本保持不變。綜合考慮網格質量對計算結果的影響以及計算的經濟性，最終選擇軸流式噴水推進模型泵的計算網格數為400 W。

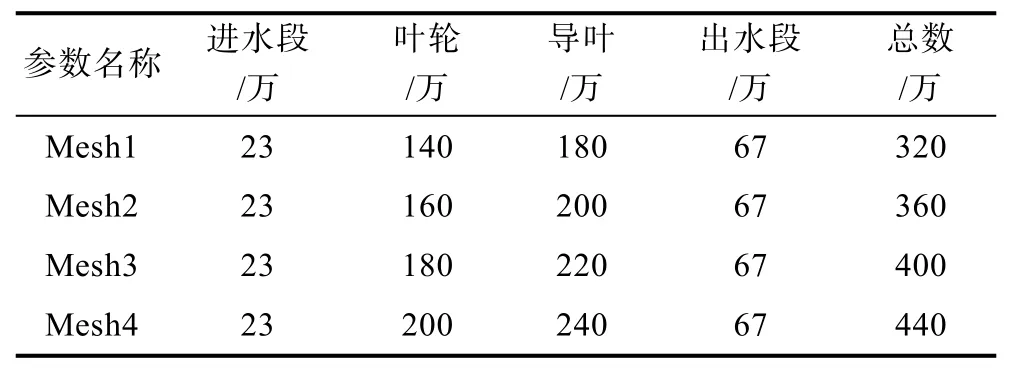
表2 軸流式噴水推進泵各流域網格劃分Table 2 Grid division of each basin of axial flow water-jet propulsion pump

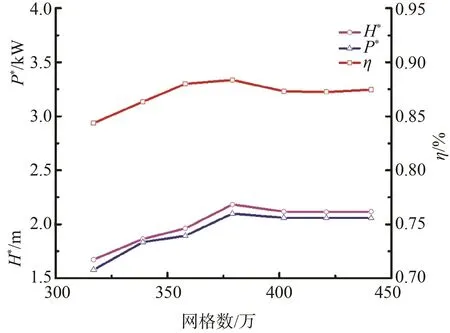
圖3 網格無關性驗證Fig.3 Grid independence verification

為了進一步對數值計算方法的準確性進行驗證，圖4和圖5分別給出了軸流式噴水推進泵在設計轉速（n=2 000 r/min）、不同流量范圍0.85～1.1 Qd*時實驗和數值計算得到的外特性曲線和設計流量下的空化特性曲線。通過對比可以看出，數值計算得到的外特性與實驗結果一致性較好，揚程、軸功率和效率誤差均在 5%以內。二者間存在誤差的主要原因是：實驗中存在彎管損失、實驗臺存在測量誤差以及實際加工精度存在誤差等。從空化特性曲線可以看出，隨著NPSH的降低，模型泵揚程起初并未發生明顯波動，當NPSH下降到11.91 m時，揚程急劇下降，數值預測的揚程隨NPSH的變化趨勢與試驗結果基本一致。試驗中模型泵臨界空化余量為11.91 m，略高于數值計算結果，這可能是由于水中可能含有少量空氣或者雜質顆粒使管路系統中發生空化。由此說明，本文所采用的數值計算方法可以較準確地對泵的性能進行預測。

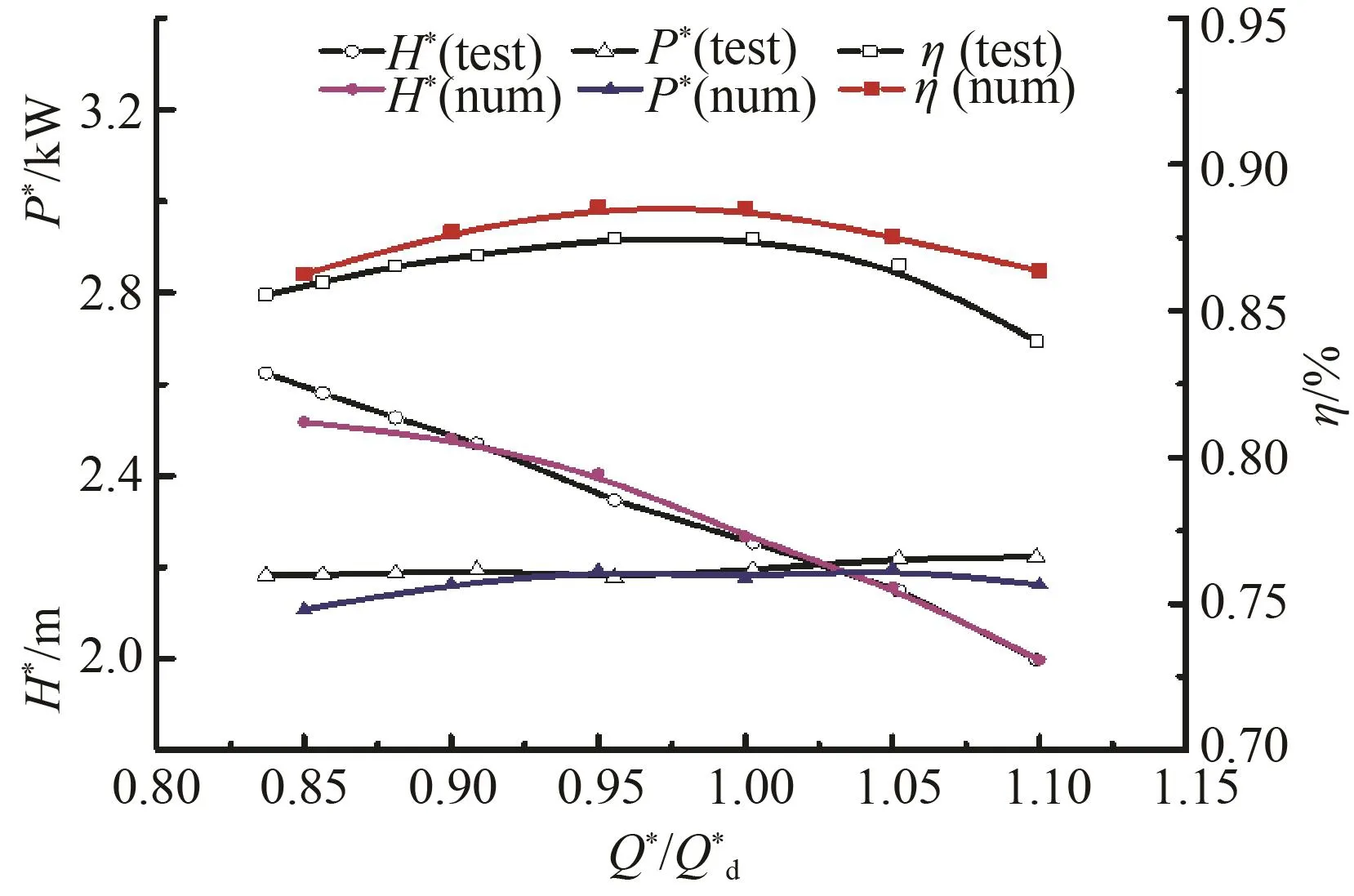
圖4 噴水推進泵外特性曲線Fig.4 External characteristic curve of water-jet propulsion pump

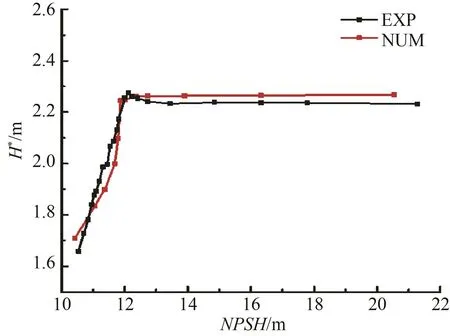
圖5 噴水推進泵空化特性曲線Fig.5 Cavitation characteristic curve of water-jet propulsion pump

2 結果與分析

2.1 噴水推進泵水力特性分析

圖6給出了設計工況下模型泵的空化特性曲線，可以看出隨著NPSH的降低，噴水推進泵的空化特性曲線可分為空化初生、空化發展以及空化充分發展 3個階段，如圖6中（Ⅰ）、（Ⅱ）、（Ⅲ）所示。在空化初生階段（12.73 m＜NPSH＜24.79 m），揚程系數基本保持不變；在空化發展階段（11.8 m＜NPSH＜12.73 m），揚程系數先在小范圍內波動，后急劇下降，在 NPSH=11.8 m時，下降幅度超過 5%，出現揚程斷裂現象；在空化充分發展階段（NPSH＜11.8 m），揚程系數進一步下降，泵無法正常工作。效率和軸功率變化趨勢與揚程變化趨勢類似。

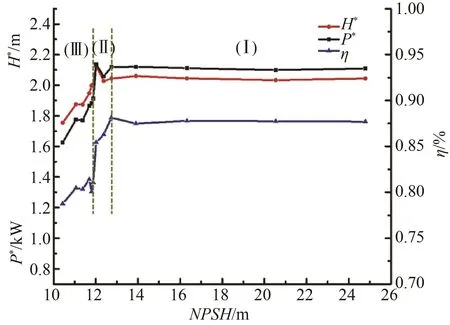
圖6 軸流式噴水推進泵空化特性Fig.6 Cavitation characteristics of axial flow water-jet propulsion pump

為進一步分析噴水推進泵的空化特性，圖7給出了不同NPSH條件下數值預測的葉輪葉片表面空穴形態與試驗的對比。從圖中可以看出，當NPSH=24.79 m時，葉輪表面未發生空化。隨著NPSH的逐漸降低，進口區域靠近輪緣處及出口區域的葉頂間隙處首先出現空化現象，并逐漸向葉片中部延伸。當NPSH進一步降低，葉頂間隙處開始發生空化，并向流道內擴張，導致間隙處局部流速升高，壓力降低，葉片工作面和背面的壓差增大，即葉片做功能力增加，揚程和軸功率升高；同時，由于葉輪旋轉與輪緣產生相對運動，導致葉頂空化形狀近似三角形，且空化區域由輪緣向輪轂延伸，當 NPSH降低至 11.8 m時，空化區域覆蓋整個葉片表面，結合圖6可以看出，此時空化特性曲線陡降，泵開始失效。

圖7 葉輪葉片表面空穴分布對比（σv=0.1）Fig.7 Comparison of cavitation distribution on impeller blade surface（σv=0.1）

圖8給出了葉輪葉片進、出口安放角等不同設計參數在設計工況下的效率曲線，其中C1和C2分別表示葉輪的進口安放角和出口安放角。從圖中可以看出，設計參數葉輪葉片進口安放角β1和出口安放角β2對推進泵的效率具有明顯影響。當 C1＞0°、C2＞0°時，推進泵的效率隨著流量的增大先增大后趨于不變；當C1＜0°、C2＜0°時，推進泵的效率隨著流量的增大呈下降趨勢，尤其是葉輪葉片進、出口安放角分別為C1=-5°和 C2=-2°時，其效率下降速率明顯增大，在Q*/Qd*=1.1時，效率已經下降至η=0.48。

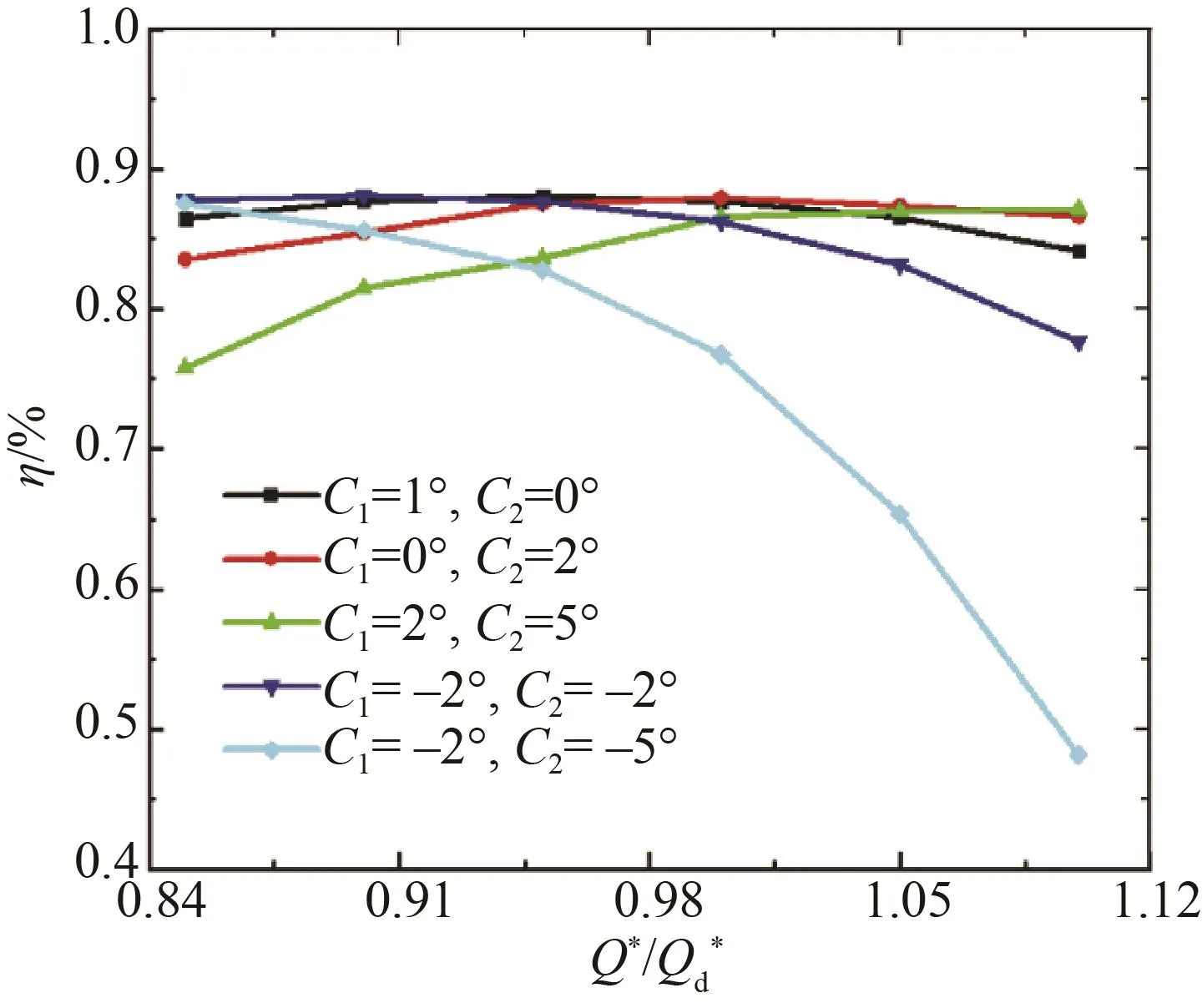
圖8 不同葉輪葉片進、出口安放角下噴水推進泵的效率曲線Fig.8 Efficiency curve of water-jet propulsion pump with different impeller blade angles at inlet and outlet

2.2 基于代理模型的結構參數優化設計

軸流式噴水推進泵的葉片安放角對其性能具有重要的影響，通過數值計算的方法尋求最優的結構參數，計算量大且計算周期較長，因此采用合理、高效的數值優化方法獲取空化性能和外特性最優時推進泵的結構參數至關重要。

2.2.1 代理模型及優化分析

軸流式噴水推進泵的葉片安放角對其性能具有重要的影響，通過數值計算的方法尋求最優的結構參數，計算量大且計算周期較長，因此采用合理、高效的數值優化方法獲取空化性能和外特性最優時推進泵的結構參數至關重要。基于代理模型的優化設計方法是一種計算量小、精度高的分析方法，其實質是通過離散的數據點，建立精度較高的數學模型，擬合出反映目標變量和自變量之間關系的函數，分析目標變量和自變量的敏感性以及對自變量取值進行尋優。基于上述的分析，本文選取葉輪進口安放角 C1和出口安放角 C2作為代理模型的自變量，選取效率和軸功率作為目標變量，具體的優化流程如圖9所示。

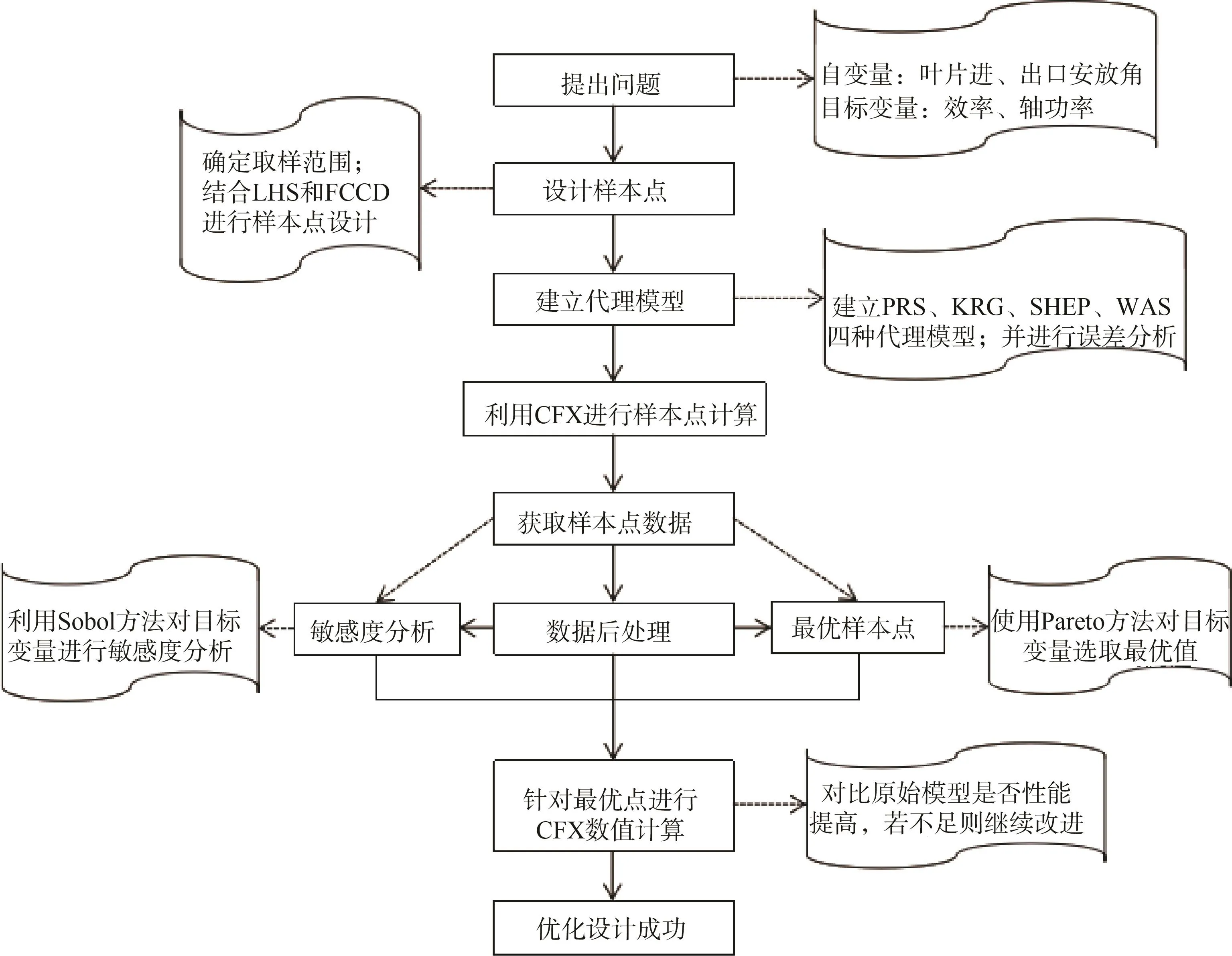
圖9 軸流式噴水推進泵優化設計流程圖Fig.9 Flow chart of optimization design for axial flow water-jet propulsion pump

選取葉片安放角為 0°時的噴水推進泵作為基礎模型，以葉輪進、出口安放角作為自變量，樣本空間取值范圍如表3。結合拉丁超立方法和中心復合法生成30組樣本點，每組樣本點包含C1、C22個參數，將樣本空間歸一化，如圖10所示，其中安放角增加-4°時為0，增加4°時為1。根據樣本點信息繪制30組噴水推進泵模型，采用CFX針對噴水推進泵進行數值計算后獲得30組目標變量值。

表3 樣本空間Table 3 Sample space

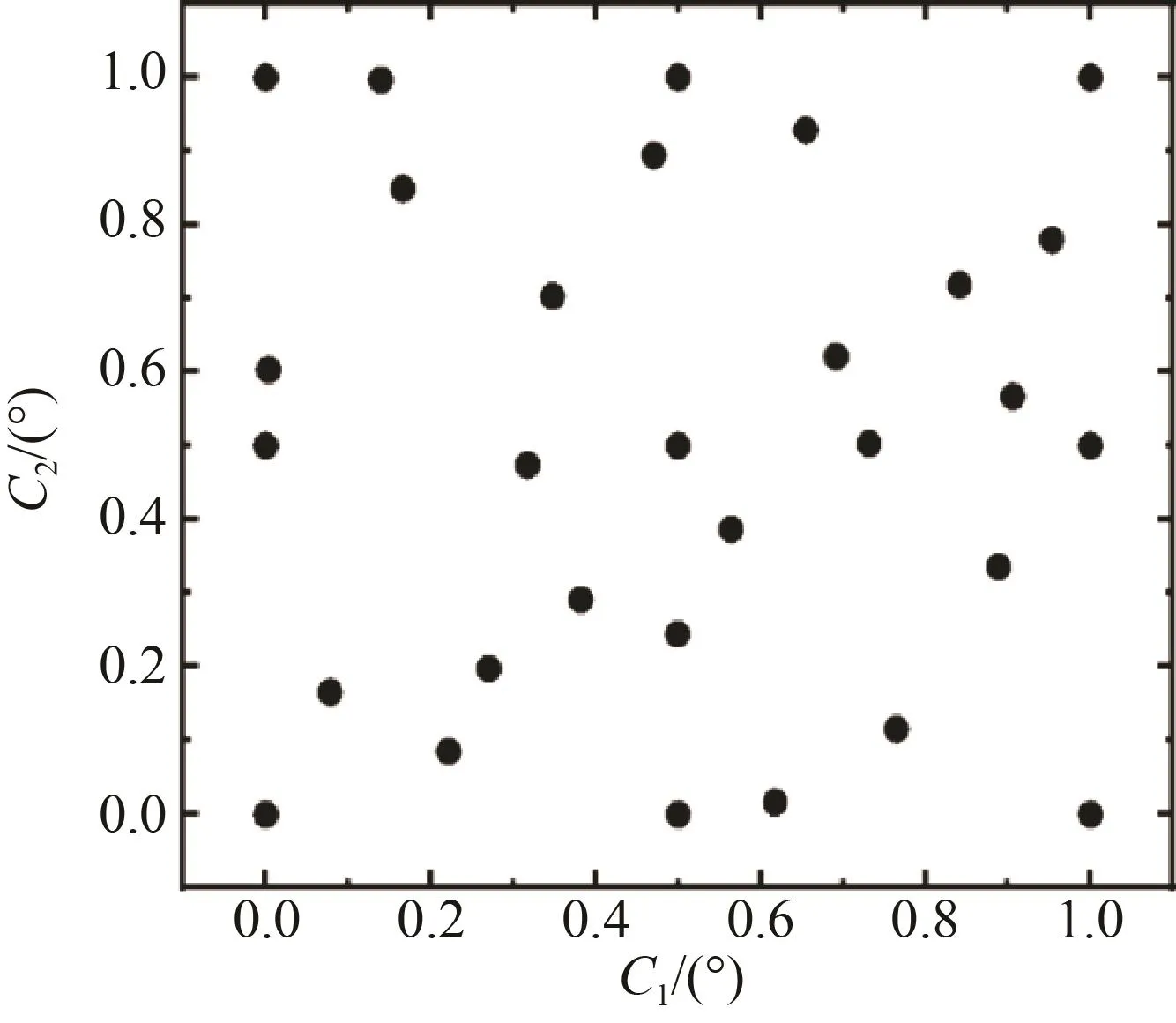
圖10 樣本點歸一化分布Fig.10 Normalized distribution of sample points

根據30組數值計算的結果分別選取Kriging模型（KRG）、項式響應面近似模型（PRS）、輻射神經元網絡近似模型（RBNN）及加權平均值近似響應模型（WAS）等4種代理模型近似方法對數值計算結果進行數據擬合，并采取均方根誤差（Root Mean Square Error，RMSE）方法針對代理模型的擬合精度進行評價，其表達式為

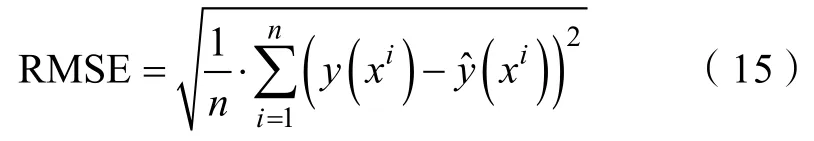
式中：n為測試點數目；xi為第i個測試樣本點；y(xi)為測試點的實際響應值；?y(xi)為預測響應值。

表4給出了各代理模型對目標變量的擬合誤差，可以看出不同代理模型對樣本數據的擬合精度存在較大差異。其中KRG模型對軸功率和效率的擬合精度最差；PRS和 RBNN模型的擬合精度較好，但仍然存在提升空間；WAS模型的擬合精度最高。由于WAS模型基于上述3種代理模型的誤差進行了權重分配，故其對目標變量的擬合精度最高。因此，本文的后續研究將采用WAS模型作為最優的代理模型。

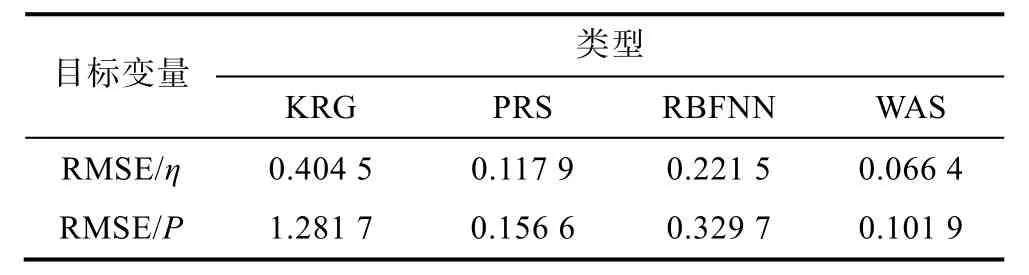
表4 代理模型誤差評價Table 4 Error evaluation of surrogate model

2.2.2 敏感度分析及結構參數優化

為了對噴水推進泵的結構參數進行優化，首先需要對涉及到的結構參數進行敏感度分析。敏感度分析是指利用代理模型對噴水推進泵在設計工況下的數值計算結果進行擬合，比較自變量的偏方差和總方差以獲得自變量β1和β2對目標變量效率η和軸功率P的重要程度分析。圖11給出了采用Sobol方法對WAS代理模型的10 000組擬合數據進行全局敏感度分析的結果，其中C1為葉輪進口安放角，C2為葉輪出口安放角。從圖中可以看出，葉輪葉片進口安放角C1在目標變量軸功率P的全局敏感度分析中所占比重為 68%，出口安放角C2所占比重為32%，說明目標變量軸功率P受葉輪出口安放角C2影響較大；而在對目標變量效率 η的敏感度分析中，各自變量所占比重差異較大，C1所占比重高達95%，而C2的比重僅為5%，說明目標變量效率η主要受葉輪出口安放角C2的影響。

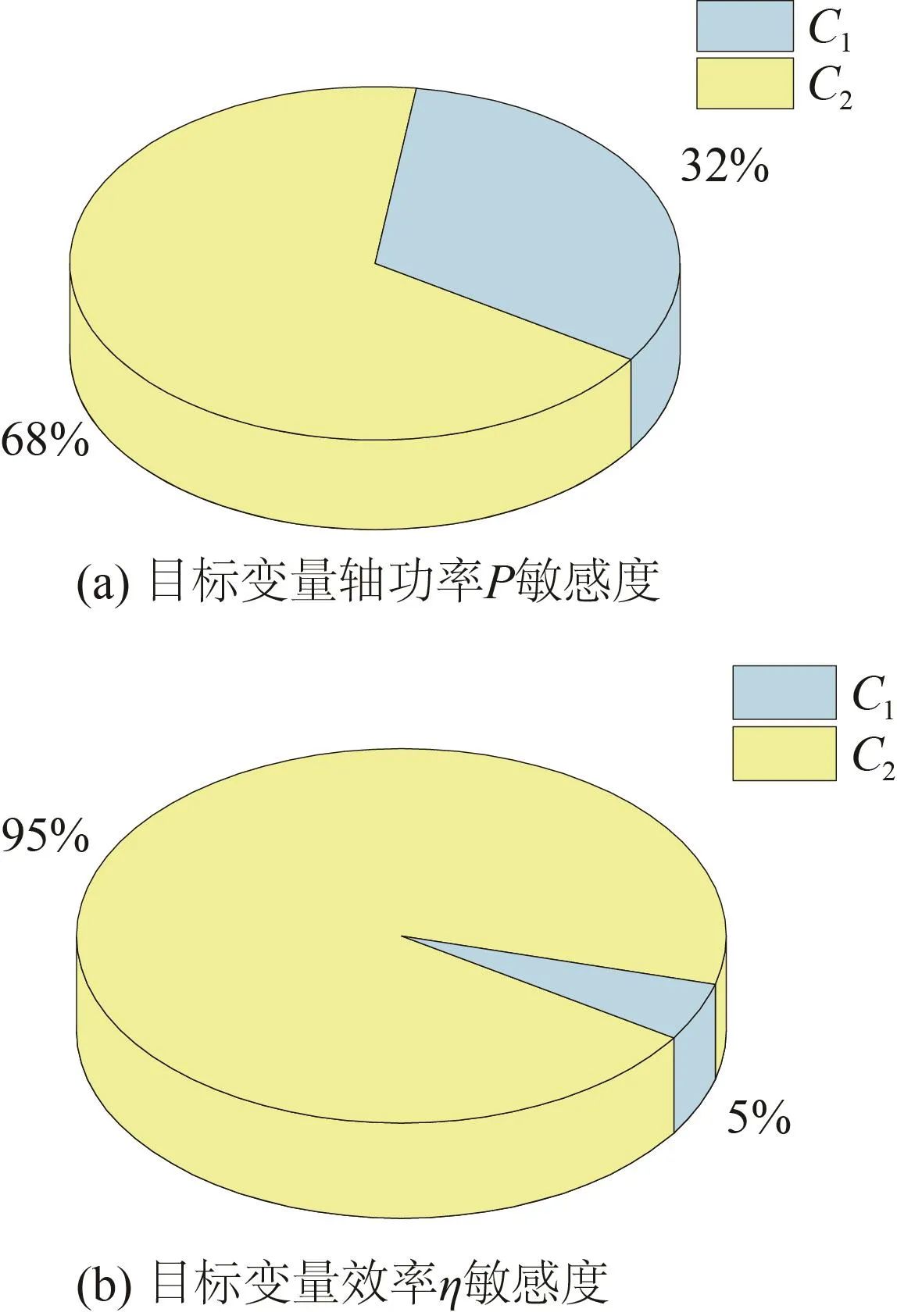
圖11 WAS代理模型自變量對目標變量的全局敏感度分析Fig.11 Global sensitivity analysis of independent variables to target variables in WAS proxy model

圖12給出了WAS代理模型擬合結果在目標變量空間中的分布情況，其中x軸為軸功率、y軸為效率，綠色圓點為10 000個樣本點。由圖可知，噴水推進泵結構參數多目標優化問題不存在最優解，所有可能的解都只滿足一個目標變量的最佳取值，并構成Pareto最優解集（紅色點集），其最優解集分布在樣本空間右上方。

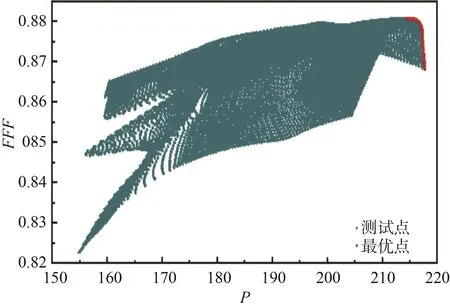
圖12 目標變量空間分布Fig.12 Spatial distribution of target variables

圖13給出了Pareto最優解集在其自變量空間的分布情況，可以看出，最優解在自變量空間內主要集中在3個區域。考慮到本次優化的最終目標是在具有較高效率的同時保證盡可能高的軸功率，為此在這3個區域分別選取一個最優的樣本點進行二次數值計算，表5為所選取的樣本點的相關參數及代理模型預測結果。

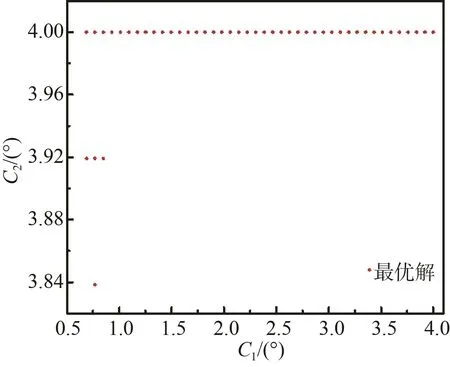
圖13 最優解集在自變量空間的分布Fig.13 Distribution of optimal solution set in independent variable space

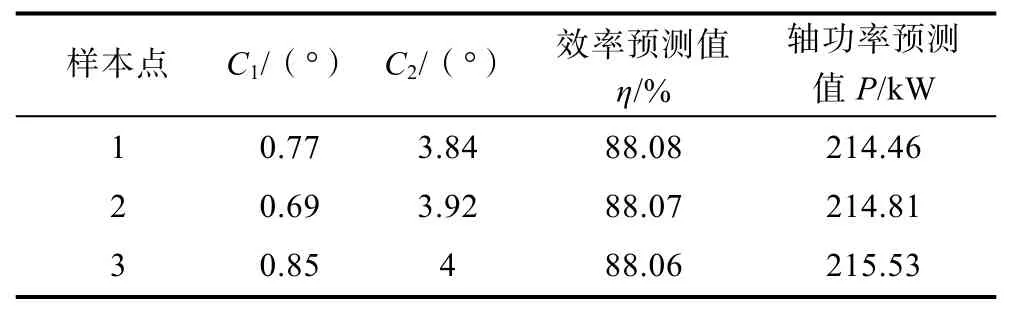
表5 3組樣本點參數及代理模型優化結果Table 5 Optimization results of parameters and surrogate model of three groups of sample points

針對上述優化點分別建立噴水推進泵模型，并采用CFX方法對設計工況下推進泵性能進行數值計算，其結果如表6所示。由表可知：設計工況下樣本點2的效率最高，樣本點3的軸功率最高。綜合上述分析，為滿足效率較高的同時軸功率盡可能高的要求，選擇樣本點2為最終優化結果，此時噴水推進泵葉輪葉片的進口安放角C1=0.69°，出口安放角C2=3.92°。

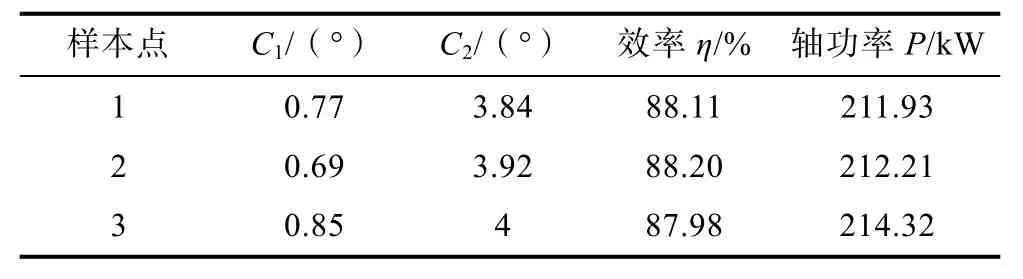
表6 設計工況下3組樣本點的數值計算結果Table 6 Numerical calculation results of three groups of sample points under design conditions

2.2.3 優化后噴水推進泵性能分析

圖14給出了優化前后噴水推進泵的外特性曲線，從圖中可以看出，優化前后的噴水推進泵外特性曲線變化趨勢基本相同，即隨流量的增加，揚程逐漸下降，軸功率逐漸上升，效率先上升后下降。優化后的揚程和軸功率在不同流量工況下較優化前均有所提升，效率的提升主要體現在在設計工況和大流量工況，其最大效率點出現在Q*/Qd*=1.0處。總體而言：優化后噴水推進泵外特性較優化前有所提升，效率最高為88.54%，較優化前提高了約1.7%；此時功率密度約為2.91 MW/m2，較優化前提高了約6%。

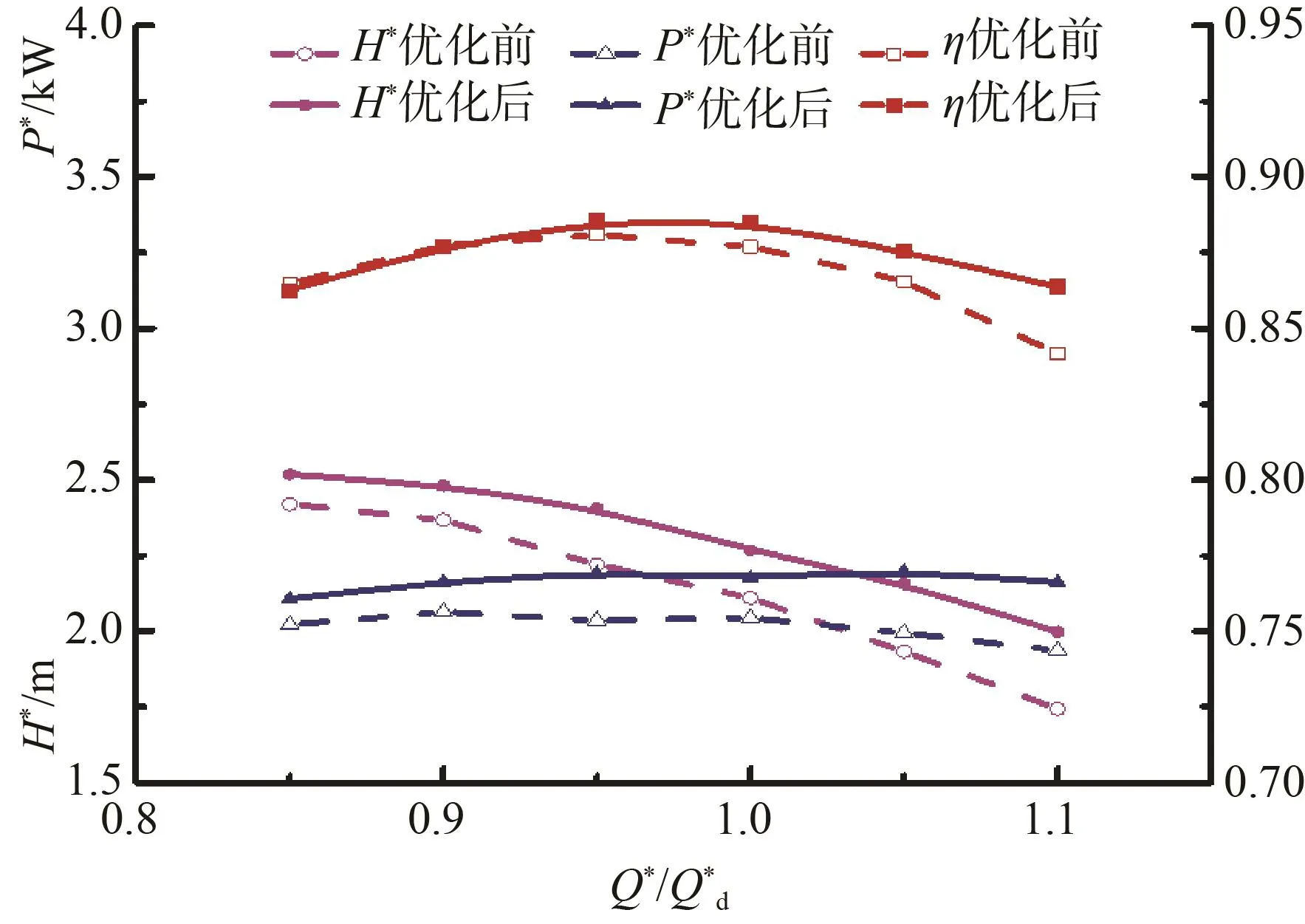
圖14 優化前后噴水推進泵外特性對比Fig.14 Comparison of external characteristics of water-jet propulsion pump before and after optimization

圖15對比了設計工況下優化前后噴水推進泵在10%、50%和90%葉高處葉輪葉片吸力面和壓力面壓力沿流向的分布，由圖可以看出，優化前后葉輪葉片表面的壓力沿流向分布規律類似，即葉輪進口及出口處壓力變化較為劇烈，葉輪中部壓力變化相對均勻。同時，優化后的葉片在10%、50%葉高處的吸力面和壓力面的壓差較優化前增大，說明噴水推進泵的做功能力增加，性能得到提升。優化后的葉片在90%葉高處的壓力分布較優化前更為均勻，說明葉輪出口處的流動脫落現象得以改善。

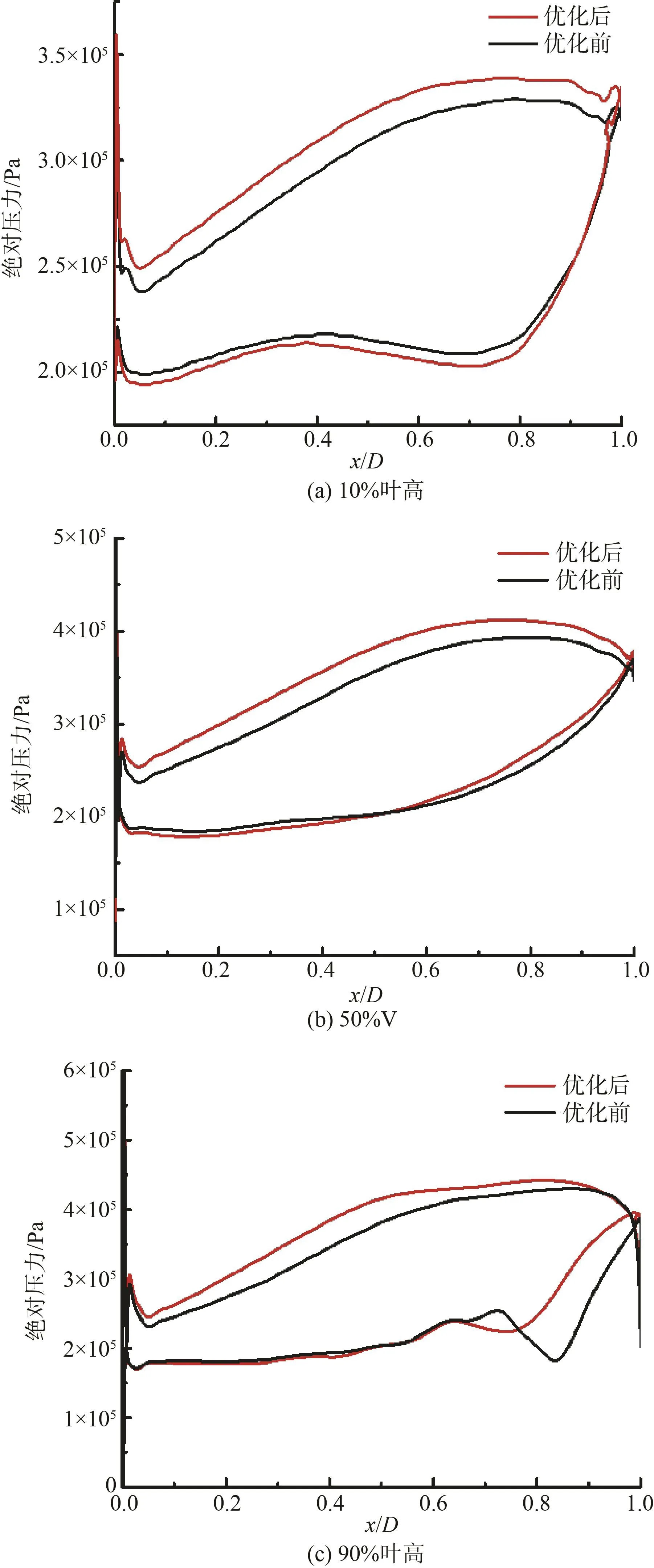
圖15 優化前后葉輪葉片表面壓力沿流向分布Fig.15 Distribution of surface pressure of impeller blade along flow direction before and after optimization

為進一步評價優化后的噴水推進泵性能，圖16給出了優化前后推進泵在不同空化階段的空穴形態對比。從圖中可以看出，隨著NPSH的下降，葉輪葉片吸力面前緣開始產生空泡，并逐漸向后發展直至覆蓋整個葉片；在相同進口條件下（即 NPSH相同），優化后的推進泵吸力面空穴面積較優化前均有所減小，說明優化后的噴水推進泵空化性能也得到了一定的提高。

圖16 優化前后葉輪葉片表面空穴形態對比（σv=0.1）Fig.16 Comparison of cavitation morphology on impeller blade surface before and after optimization（σv=0.1）

3 結束語

本文基于旋轉修正的SST k-ω湍流模型和Zwart空化模型對軸流式噴水推進泵的水力特性進行了數值計算研究，基于數值計算結果，采用代理模型優化方法，對噴水推進泵的葉輪進出口安放角等結構參數進行了優化設計，得到以下結論：

1）采用的數值計算方法能夠準確地預測噴水推進泵的外特性和空化特性，并基于數值計算結果發現葉輪的進口安放角和出口安放角對噴水推進泵的水力特性影響較大。

2）通過代理模型優化分析，噴水推進泵葉輪出口安放角對其效率和軸功率影響占比分別約為 95%和68%，進口安放角對其效率和軸功率影響占比分別約為5%和32%，說明噴水推進泵效率和軸功率主要受葉輪出口安放角的影響。

3) 當葉輪進口安放角和出口安放角分別為0.69°和3.92°時，滿足Pareto最優解，此時噴水推進泵效率較優化前提高了約 1.7%，功率密度較優化前提高了約6%，模型泵的整體優化效果明顯。