基于RABT火災曲線的沉管隧道管壁一維溫度場解析
吳慶良,吳夢軍,鄧小華,胡學兵,曹 鵬
(1. 招商局重慶交通科研設計院有限公司,重慶 400067;2. 西南大學 工程技術學院,重慶 400716;3. 公路隧道建設技術國家工程實驗室,重慶 400067;4. 廣東省交通集團有限公司,廣東 廣州 510000)
0 引言
沉管隧道由于其地質適應能力強、通行能力強、對周邊生態環境影響小且具有不占航道等優勢,不僅成為修建跨江越海通道的重要工法,而且在城市水下隧道工程中也得到了廣泛應用[1-2]。自19世紀末美國第1次采用沉管法修建水下隧道以來,至今世界上已建成的沉管隧道超過150座[3]。近40 a時間內,我國已建成沉管隧道近20座,包括早期的廈門翔安海底隧道及近期的港珠澳沉管隧道等[4-5]。
在海底沉管隧道給人們生產、生活帶來便利的同時,作為主要災害的火災也頻繁發生,不僅會造成嚴重的人員傷亡,而且火災高溫還會導致混凝土爆裂和力學性能的劣化,對襯砌結構產生不同程度的損壞,大大降低結構的承載力和安全性。因此,研究隧道火災發生后隧道襯砌結構厚度方向的溫度場分布具有重要意義。
目前已有較多學者針對這一問題開展了大量研究,如蔣樹屏等[6]為了解沉管隧道火災發生時其周圍溫度場的分布規律及其影響因素,建造沉管隧道試驗平臺,采用1∶1足尺火災試驗和FDS數值仿真計算相結合的方法,對沉管隧道火災發生時隧道內溫度場的分布規律進行了系統研究。Guo等[7]、張祝永等[8]依托港珠澳大橋沉管隧道工程,利用ANSYS軟件分析了火災下沉管隧道的溫度場和應力分布特點。趙志斌[9]以長江隧道為依托,模擬了不同火荷載作用下襯砌結構溫度應力的分布規律,并找出了最易破壞的部位。張孟喜等[10]用有限元程序模擬了火荷載作用下沉管隧道結構溫度場及應力場,并根據計算結果,結合大量的隧道火災資料總結了火災時隧道內部的溫度場及應力場的危險區域。Yan等[11]、朱合華等[12]針對特長公路隧道發生火災特點,借助大比例火災模型試驗,系統研究了火災時隧道內溫度隨時間的變化和最高溫度與通風風速、火災規模的關系。
通過文獻調研可知,目前有關隧道火災溫度場分布規律方面的研究主要是采用火災試驗和數值模擬2種方法進行,有關隧道在火災時瞬態溫度場演化的解析研究成果相對較少,相對而言,解析解更具備通用性,便于一般規律的探討,因此,本研究結合沉管隧道遭受火災時的實際工況建立相應的數學模型,并基于已有初始條件和邊界條件,采用2次分離變量法求得RABT火災曲線的沉管隧道管壁厚度方向的溫度場解析解,最后采用廣東某沉管隧道參數對管壁不同位置和不同時間的溫度場分布規律進行探討。
1 求解的基本方程
1.1 火災曲線
為了定量評定隧道襯砌結構的耐火性能,國內外相關單位及學者基于開展的大量足尺火災試驗成果,建立了一系列不同類型的火災曲線,用來反映隧道火災時溫度隨時間的變化歷程。國外比較常用的如國際標準化組織制定的 ISO834曲線[13]、美國和加拿大采用的 ASTM-E119曲線[14],HC曲線和HCint曲線[15]等。
上述各類火災曲線都體現了隧道內火災升溫速度快這一顯著特點,但由于各標準曲線是在不同火災試驗基礎上建立起來的,各自的升溫過程及達到的最高溫度有所差異。我國現行《建筑設計防火規范》(GB50016—2014)[16]在綜合考慮上述標準火災曲線及火災場景的基礎上,對城市隧道承重結構體耐火極限測試時選用的標準升溫曲線做出了相應規定,本研究相關內容均是基于該規范中的RABT火災曲線,函數表達式如下:
(1)
式中,T(t)和T0分別為RABT火災曲線函數和結構初始溫度;t為火災持續時間。該曲線可以表現汽車在隧道內發生火災時的燃燒特性,其火災溫度的發展趨勢為:火災時隧道內溫度在 5 min 時從常溫T0升到最高的 1 200 ℃;最高溫度持續了90 min后開始下降;降溫過程為30 min,到第125 min時溫度將到常溫T0。
1.2 數學模型與初始、邊界條件
考慮管節的施工制作工藝及空間利用率等方面,目前沉管隧道主要采用矩形截面形狀,如港珠澳沉管隧道標準管節的橫斷面寬度達到37.95 m×11.4 m (寬×高)。在求解沉管隧道沿壁厚方向的溫度場分布時,可將研究問題近似簡化為如下一維瞬態熱傳導模型,將襯砌結構混凝土視為均質、連續的介質,且不考慮鋼筋、鋼纖維的影響。沉管隧道在實際火災情況下,管節內壁為受火表面,熱流溫度及沉管結構內表面與熱煙氣流間的對流換熱系數均可測定,屬于第3類邊界條件。管節外壁處由于被回填土體包圍,并且混凝土材料具有熱惰性,結構厚度大(一般都超過1.4 m),其外側界面溫度一般不會太高,與回填土體溫差不大,可假定沉管隧道結構混凝土與回填土體之間為理想接觸,即不考慮二者之間的接觸熱阻。
本研究的最終數學模型及初始、邊界條件如下。
瞬態熱傳導微分方程:
(2)
邊界條件:
(3)
初始條件:
T(y, 0)=T0(y),
(4)
式中,T(y,t)為管節結構中任意時刻t任意位置y的溫度;相應的T(0,t)為管壁靠海水側任意時刻的溫度;T(d,t)為管壁受火側任意時刻的溫度;T(y,0)為管節任意位置初始時刻的溫度;ac為混凝土的導溫系數,且ac=λ/cρ,λ,c,ρ分別為混凝土的導熱系數、比熱容和密度;d為沉管隧道承受火災處管壁厚度;Tw為隧道外海水和覆土的溫度;hf為管節結構內表面與熱煙氣流間的綜合換熱系數,即對流換熱系數與等效輻射換熱系數之和,Tf(t)為管節內壁附近的熱流溫度,并假定溫度分布服從RABT曲線;T0(y)為隧道管壁混凝土的初始溫度場分布,火災常發生在運營隧道,故而可取為常溫,即環境的溫度Ta。
本研究問題相應的計算模型見圖1。為說明一般規律性問題并簡化計算,本研究中混凝土的熱工參數均取為常數,即不隨溫度的升高而改變。
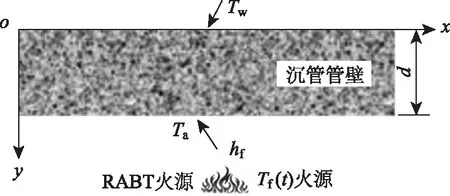
圖1 計算模型示意圖
2 求解的基本方程
工程中由于邊界條件的復雜性及方程中物理參數的非線性,造成大多數偏微分方程的解析解求解過程十分困難,并且也僅限于幾類特定的數學方法,如分離變量法、拉普拉斯變換、格林函數法等[17]。對于本研究的問題,基于已有初始條件和邊界條件,可采用2次分離變量進行求解。
首先對求解問題的邊界條件齊次化,令:
T(y,t)=v(y,t)+w(y,t),
(5)
則求解的數學問題變為下面2個問題。
問題1:v(y,t)是滿足基本方程及邊界條件的1組特解,通過分離變量法和觀察法可構造如下解[18]:
v(y,t)=φ+(η-φ)y/d,
(6)
式中η,φ為待定系數,可代入邊界條件求解得:
φ=Tw,
(7)
(8)
式中Tf(t)為RABT曲線方程,函數表達式即式(1)。
問題2:w(y,t)是滿足基本方程和齊次邊界條件的1組通解,此時初始條件也進行了相應變化,
微分方程:
(9)
邊界條件:

(10)
初始條件:
w(y,0)=Ta-v(y,0),
(11)
式中χ,ω為待定系數,同樣根據邊界條件求解得:
(12)
(13)
問題2為熱傳導問題的定解問題,可進一步采用分離變量法和常數變易法進行求解[18]。
下面先采用分離變量法來求解滿足邊界條件的固有函數系。
令w(y,t)=ξ(y)·ζ(t),其中ξ(y),ζ(t)為待定函數,代入方程(10)中有:
ξ(y)·ζ′(t)=ac·ξ″(y)·ζ(t)。
(14)
由于w(y,t)≠0,即ξ(y)≠0,ζ(t)≠0,則上式可變為:
(15)
上式成立,則其必等于同一非正常數(設為-ζ2),可得:
ξ″(y)+ζ2·ξ(y)=0,
(16)
ζ′(t)+ζ2·ac·ζ(t)=0。
(17)
根據式(16)及相應的邊界條件可獲得固有函數如下:
ξn(y)=Cn·sin(ζy),n=1, 2,…,m,
(18)
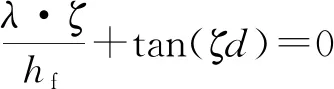
根據常數變易法,假定問題2的特解有如下的形式:
(19)
式中Bn(t)是待定函數;ζn為超越方程λ·ζ+hwtan(ζd)=0的根。為了確定Bn(t),現按照固有函數系展開成如下級數形式:
(20)
根據正弦函數正交性,可求得:
(21)
式中ψn為系數,可通過下式求解:
(22)
將式(19)和式(21)代入非齊次微分方程(9),得到:
(23)
由此可得:
(24)
可求得:
(25)
式中Dn為待定系數,代入初值條件進而可求得:
(n=1, 2,…,m)。
(26)
綜上可知,本研究問題中海底沉管隧道的一維瞬態溫度場的通解為:
sin(ζny),
(27)
式中,
(28)
(29)
式中,Tf(t)為RABT曲線方程,ζn為超越方程λ·ζ+hwtan(ζd)=0的根。
3 算例驗證及分析
以廣東某沉管隧道為例,該隧道管節結構采用C50混凝土材料,管壁厚度為1 500 mm。為說明一般規律性問題,本研究取混凝土的熱工參數為常數,即導熱系數λc=1 W/(m·K),比熱容Cc=1 000 J/(kg·℃),密度為ρc=2 400 kg/m3,對流換熱系數為hc=25 W/(m2·℃)。隧道火災發生時一般為運營階段,此時隧道外側被常溫(Tw=20 ℃)的海水和回填土體包圍,并假定管節內部已無水化熱產生,初始溫度場也為常溫Ta=20 ℃。
3.1 不同時間的溫度分布及解析過程的驗證
為驗證上述解析解的正確性,采用COMSOL軟件建立數值模型,模型尺寸設定為1個混凝土澆注倉大小(3 500 mm×1 500 mm),模型左右邊界設置為熱絕緣屬性,上邊界設置為海水溫度Tw=20 ℃,下邊界設置為對流熱通量,對流換熱系數為hc=25 W/(m2·℃),外部火源溫度設置為RABT曲線,其余模型參數與上述算例中一致,完整網格包含10 706 個域單元和286 個邊界元,采用瞬態求解器求解,相對容差取0.01。計算模型與125 min結果如圖2所示。
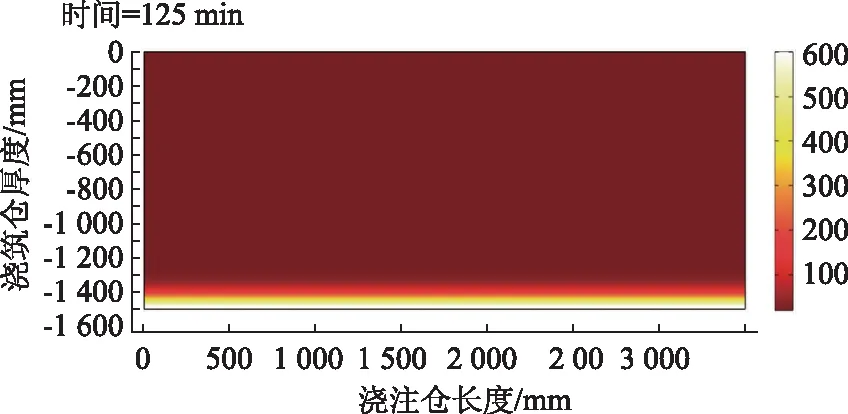
圖2 COMSOL計算模型與125 min的計算結果
沿管壁厚度方向取5個監測點(數值模型中y軸正負號對計算結果沒有影響,只是坐標系標注不同而已,分別取值y1=1.50 m,y2=1.49 m,y3=1.45 m,y4=1.40 m,y5=1.30 m)。圖3為各監測點在125 min的時間域內的溫度變化曲線,散點值表示COMSOL模擬計算的結果,曲線值表示解析解的結果。可以看出,不同位置處數值計算結果的散點值均與解析解計算的曲線值重合,說明上述解析解的計算結果與數值模擬結果是吻合的,由此驗證了解析解的正確性。
從圖3可以看出,管壁靠受火面位置y1=1.50 m,y2=1.49 m這2處的溫度在關鍵時間節點處有突變,如在t=5 min之前,曲線斜率較大,而之后斜率逐漸變小,即溫度增長速度變緩;而在t=95 min之后曲線斜率變為負值,曲線開始下降,進入降溫階段,且更靠近管壁受火面位置y1=1.50 m處的降溫速度更快。
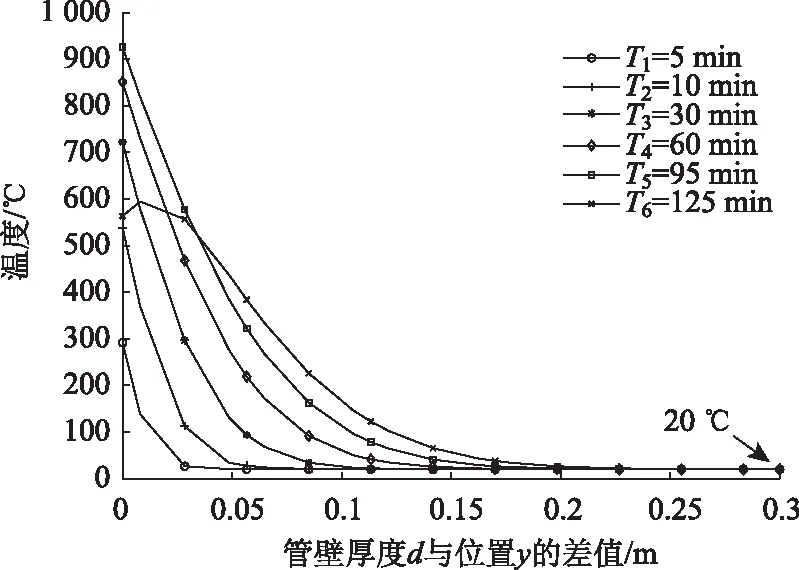
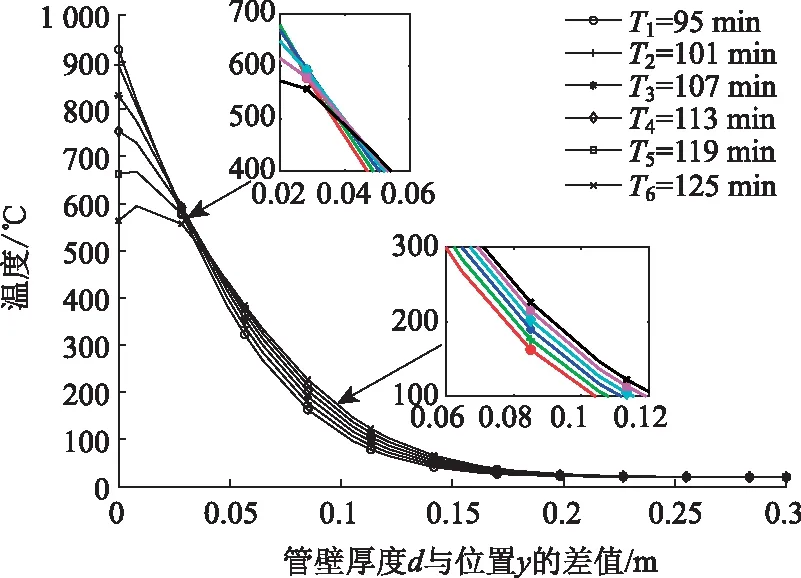
在沉管管壁上各測點的時間-溫度曲線和RABT曲線并不是嚴格一致,原因主要是由于混凝土材料的比熱容造成了溫度傳遞的滯后。受此滯后效應影響,在火災恒溫階段時(5 min 從圖3還可以看出,在火災升溫、恒溫和降溫全過程中,位置y5=1.30 m處的溫度變化都很小,即火災高溫對沉管管壁的影響深度在20 cm左右,這與參考文獻[11]中的相關結論也較為吻合。 圖3 管壁不同深度處溫度場隨時間的分布規律 圖4給出了管壁30 cm范圍內的Ti=5,10,30,60,95,125 min,i=1,…,6共6個具有代表性的時間點的深度-溫度曲線。可以看出,除T6=125 min 時間點外,其他5條曲線呈現明顯的單調遞減規律,即溫度從外到內依次降低;而在T6=125 min 時刻,管壁內部某些區域的溫度高于外側,即有較高的殘余溫度,主要原因仍是由于混凝土材料熱惰性造成溫度傳遞滯后的影響。 圖4 不同時間點的管壁溫度場隨深度的分布規律 管壁溫度內高外低現象主要發生在降溫階段(95 min 圖5 降溫階段不同時間點的管壁溫度場隨深度的分布規律 從圖5可以看出,降溫過程中,在T5=119 min,T6=125 min這2個時刻,管壁內部某些區域溫度高于外部,分析原因主要有2方面:一方面是由于3.1節所提到的混凝土材料的熱惰性影響,內部溫度持續增長,另一方面因為管節腔體內火源溫度被降下來之后(119 min時為256 ℃,125 min時為常溫20 ℃),而管壁對應時間的溫度分別為663.21 ℃和563.23 ℃,會反向散熱,對隧道腔體產生熱輻射和熱對流,溫度下降較快。 (1) 采用2次分離變量法求得RABT火災曲線的沉管隧道管壁厚度方向的溫度場解析解,并運用COMSOL軟件對算例進行了數值模擬計算。不同位置處數值計算結果的散點值均與解析解計算的曲線值重合,驗證了前述解析過程的正確性。 (2) 由于混凝土材料的熱惰性造成了溫度傳遞的滯后,從而使得沉管管壁上各測點的時間-溫度曲線和RABT曲線并不是嚴格一致,但在關鍵時間節點處仍有突變效應,且更靠近管壁受火面位置處的降溫速度更快。火災高溫對沉管管壁的影響深度在20 cm左右。 (3) 由于管壁溫度傳遞滯后效應的影響,在火災恒溫階段時,管壁靠受火面位置處的溫度仍然在增長,并在t=95 min時達到最大值,甚至在火災降溫過程中,管壁靠內部位置的溫度也一直在增長,并在t=125 min時達到最大值。 (4) 降溫過程中,由于混凝土材料的熱惰性及隧道腔體溫度較低,管壁會反向散熱,在T5=119 min和T6=125 min這2個時刻,管壁內部某些區域溫度內高外低,即降溫結束后管節內部仍有較高的殘余溫度,后續仍有可能會對管節造成進一步的損傷。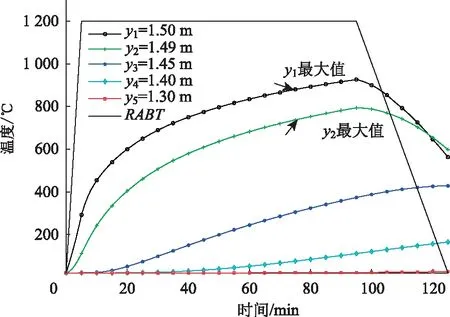
3.2 沿管壁厚度方向的溫度分布規律
4 結論

