傳奇入學題成了名梗：證明π＞3.05

七君

上名校是大多數中學生的夢想，日本的小朋友也不例外。日本人心中的最好國內大學是東京大學。東京大學在2022年QS世界大學排名中是第23位（清華和北大分別為第17位和第18位），是日本上榜學府中的第一名。

東京大學出了一道題

東京大學的入學測試和其他大學不一樣，國考的占比只有20%，日本的高考制度和我國不太一樣，他們除了全國性的統一考試，也就是全國共同學歷第一次考試（UECE）外，每個公立學校還有各自的入學測試，其他日本公立大學規定的國考占比是40%～60%，校考的占比達到80%，因此也是最難考入的高等學府。

東京大學大講堂

在2003年的入學測試中，東京大學理學院入學考試的第六題考了一道看起來非常簡單的題，但是這道題卻把日本中學生難倒了，被日本人稱為“傳說中的東大入學題”。一些知名漫畫也拿這道證明題玩梗，比如《龍櫻》。

漫畫《龍櫻》中調侃東京大學的這道入學測試題

這道題就是：證明圓周率π大于3.05。其實，要證明圓周率大于3.05并不是那么困難。日本小朋友證明不了，和他們的教育體制有些關系。我們先來看怎么證明。

在回答這個問題之前，首先了解一下什么是圓周率。圓周率的定義是圓的周長和直徑的比，利用這個定義就可以證明圓周率大于3了。

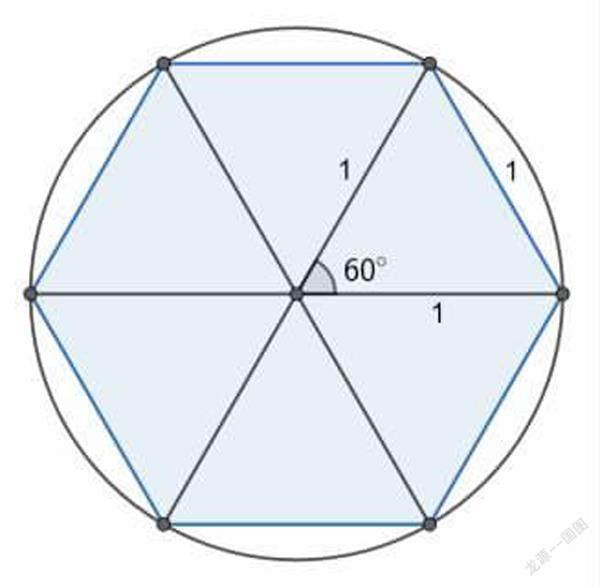
一個圓里有一個正六邊形

比如，在一個半徑為1的圓里面有一個正六邊形，可知圓的周長大于正六邊形的周長，也就是：2π>6 ，因此：π>3，很容易就能證明圓周率大于3。那么怎么證明圓周率大于3.05呢？

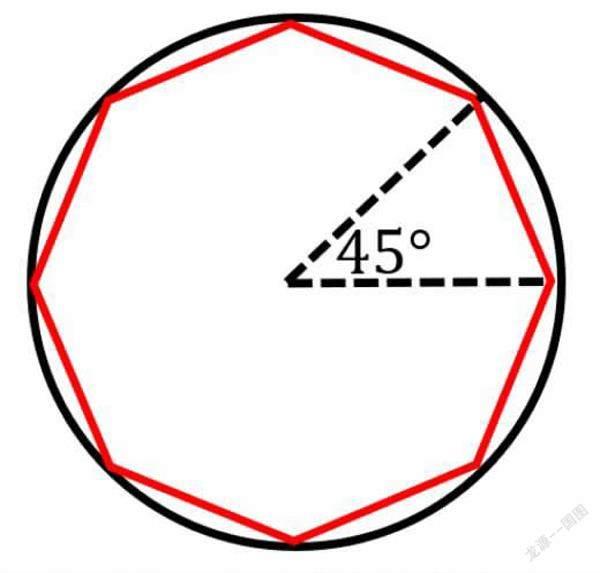
一個圓里有一個正八邊形

最簡單的方法，就是作一個半徑為1的圓，然后在圓里作一個正八邊形。顯然，圓周長大于正八邊形的周長，所以只要求出正八邊形的周長就可以證明圓周率大于3.05了。那么怎么計算正八邊形的周長呢？算每條邊長就好了。正八邊形可以分成8個等腰三角形，每個三角形的頂角為45度。根據余弦定理（勾股定理的普適版本，描述三角形中三邊長度與一個角的余弦值關系的定理），這個正八邊形的邊長是：

因為圓周長大于這個正八邊形的周長，所以：

2π>8

因此：

π>4

把右邊算一下，就可以證明圓周率大于3.05。另外一個方法是把圓十等分。

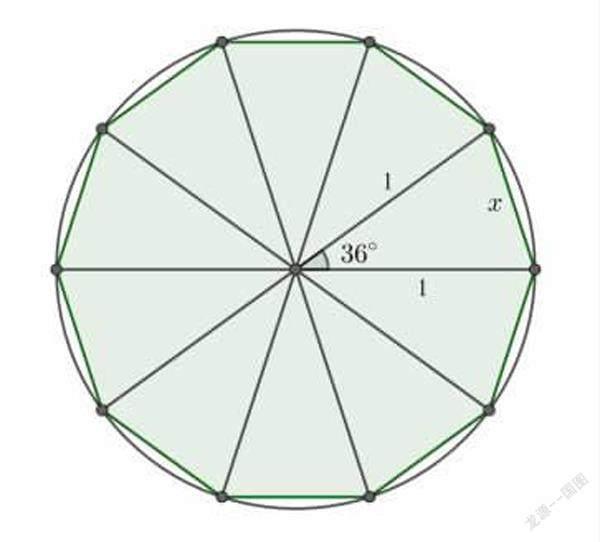
一個圓里有一個正十邊形

十等分后，每個三角形的頂角是36度。那么根據余弦定理，底邊邊長x 就是：

x2=1+1-2cos36°

中學里有教過，頂角是36度的等腰三角形和黃金分割有關：

2cos36°=

因此正十邊形的邊長為：x=0.618...>0.61，又因為圓周長大于正十邊形的周長：2π>10x，可知：π>5x>5×0.61=3.05。

減負和寬松教育的利弊

上面說的是這道題的幾種破題法，但是這道題走紅的真正原因，是東京大學悄悄嘲諷日本政府減負政策的舉動。剛才說到東京大學的這道題是2003年出的。而在2002年，發生了一個重要的事件：日本實行了減負政策改革，也就是寬裕教育。為日本政府提出的寬裕教育充當發言人的文科省審議官、京都造形藝術大學教授寺脅研表示，從明治維新到1977年，日本采取的是填鴨式教育模式，中小學的學習內容不斷增加。他指出，不可否認的是，這對日本的現代化起到了重要作用。但是，因為學習內容的增加，在70年代末，這樣的填鴨模式開始反噬社會，當時的日本中學輟學問題嚴重，校園暴力也不斷升級。在這樣的背景下，日本政府開始進行教育改革。

從20世紀70年代開始，日本政府逐漸減少了小學生的上課時間，降低了課程內容和強度，并進行了幾次重要的改革。比如，面對日本社會對“填鴨教育”的質疑，1985年日本內閣設置了臨時教育審議會，提出了重視個性原則、終身學習、教育國際化接軌等改革方針，這就是日本的第一次減負。

在1992年，日本政府又再次為學生減負。寺脅研表示，第三次重大改革是2002年4月開始的。當時，日本教職員組合（日教組）提出了“有寬裕的學校”的教育理念后，日本內閣提出了“公共教育民營化、自由化”。接著，日本文部省與中央教育審議會出臺了重視“寬裕”的《學習指導要領》，該政策從2002年度起正式實施，后來這種新的減負教育就被稱為“寬裕教育”。

2002年寬裕教育的主要改革內容包括刪減學習內容和授課時長、全面實行每周5天的學制。也就是說，在2002年的改革后，日本的小學生除了作業變少、課堂內容變簡單之外，終于不用在周六上學了。但是，2002年的寬裕教育也飽受爭議，日本社會認為寬裕教育培養出了一批學習能力低下的廢柴，而這個年齡段的學生也被稱為“寬松世代”。寺脅研說，在2002年的改革后，因為日本人擔心日本學生的學力下降，作為發言人的他也經常遭受抨擊。

而在2002年的寬裕教育中，作為標志性的“降智打擊”的改革措施，就和圓周率有關。原來，日本政府在2002年修改了小學的教材，將圓周率取值為近似值3，引起了軒然大波。日本最大的課外培訓機構之一的日能研就在東京的電車里張貼了大量的吐槽廣告。新聞媒體和周刊雜志也對這個事件進行了大量報道。東京大學在改革次年出的這道入學測試題在日本迅速走紅，就是因為這個原因。

其實歷史上出現過不少類似的嘗試用行政或法律手段強迫常數變節的事件。比如在1897年的美國印第安納州議會上，業余數學家 Edward J. Goodwin 堅信自己提出的化圓為方的方法是對的，因此把自己的這個錯誤方法作為法案提出。按照 Goodwin 的算法，圓周率就會變成3.2，而不是3.14……

那天，幸好普渡大學的數學家 C. A. Waldo 在場，他及時否定了這個提案，阻止其成為法律。但是這個事件后來鬧得沸沸揚揚，《芝加哥論壇報》等主流報紙也開始跟進報道，因此這個法案后來也被稱為“圓周率法案”。在美國沒有通過的法案，卻在日本小學里實現了，難怪東京大學的出題老師也看不下去了。

可是，日本社會是不是焦慮過度了呢？其實，在2002年的寬裕教育政策落地一年后，日本16歲中學生在經濟合作與發展組織籌劃的知名國際學生學業評估測試——國際學生評估計劃 （PISA2003），以及國際數學與科學趨勢研究報告2019（TIMSS 2003）中的各個學科的排位均下滑了。比如，2003年日本在PISA數學測試中的排名從3年前的第1名下降到第4名，2006年更是下滑到第10名，這令日本人感到十分羞恥。

因此在2008年，安倍內閣又推倒了之前的寬松快樂教育，提出了增加學習難度的新版《學習指導要領》。日本媒體把這次改革稱為脫寬裕教育。脫寬裕教育改革從2011年開始正式實施。脫寬裕教育改革的第二年，也就是2012年，日本在PISA數學測試中的排名為第7名，2015年、2018年則分別為第5和第6名，較2006年有所上升，但沒有再次榮登榜首。

（本文經授權轉載自“把科學帶回家”公眾號，有刪節）