基于多分辨率生成對(duì)抗網(wǎng)絡(luò)的空間數(shù)據(jù)不確定性重建方法
管其杰,張 挺*,李德亞,周紹景,杜 奕
(1.上海電力大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院,上海 200090;2.上海第二工業(yè)大學(xué)工學(xué)部,上海 201209)
0 引言
空間數(shù)據(jù)是數(shù)據(jù)的一種特殊類型,兼具結(jié)構(gòu)性和隨機(jī)性[1]。目前,重建大范圍、真實(shí)、有效的空間數(shù)據(jù)比較困難,主要原因在于科學(xué)實(shí)驗(yàn)和勘探開(kāi)發(fā)費(fèi)用高[2]。
數(shù)據(jù)插值成為重建空間數(shù)據(jù)的一個(gè)有效手段[3]。插值方法分為“確定”性插值方法和“不確定”性插值方法。不確定性插值方法的不確定性主要表現(xiàn)在插值結(jié)果的不確定性和多樣性,但是這些結(jié)果是對(duì)訓(xùn)練數(shù)據(jù)的統(tǒng)計(jì)特征的呈現(xiàn),具有較強(qiáng)的指導(dǎo)意義[4]。不確定性插值方法主要包括克里金(Kriging)方法和隨機(jī)模擬方法。多點(diǎn)統(tǒng)計(jì)法(Multiple-Point Statistics,MPS)是目前隨機(jī)模擬的主流,其特點(diǎn)是基于訓(xùn)練圖像(Training Image,TI)進(jìn)行建模,本質(zhì)上是基于概率統(tǒng)計(jì)思想進(jìn)行特征提取和特征復(fù)制。近年來(lái),MPS得到了廣泛應(yīng)用并發(fā)展了一些變體,如SNESIM(Single Normal Equation SIMulation)[5]、FILTERSIM(FILTER-based SIMulation)[6]、DS(Direct Sampling)[7]等。SNESIM算法通過(guò)統(tǒng)計(jì)待模擬點(diǎn)與周圍條件數(shù)據(jù)點(diǎn)構(gòu)成的數(shù)據(jù)事件在訓(xùn)練圖像中出現(xiàn)的概率,利用馬爾可夫蒙特卡羅法抽樣,完成待模擬點(diǎn)的隨機(jī)模擬。FILTERSIM算法引入了一系列不同方向的線性濾波器對(duì)訓(xùn)練圖像進(jìn)行過(guò)濾和分類。DS算法根據(jù)已知空間數(shù)據(jù)信息,通過(guò)計(jì)算距離選擇已知區(qū)域中最佳匹配的訓(xùn)練模式作為待模擬點(diǎn)的模式。但是上述這些方法耗時(shí)較長(zhǎng)且CPU占用率高。流行學(xué)習(xí)的應(yīng)用是通過(guò)從高維空間中提取低維的流行結(jié)構(gòu)實(shí)現(xiàn)對(duì)高維數(shù)據(jù)的降維,來(lái)提高重建的速度,但是本質(zhì)上不能降低對(duì)空間訓(xùn)練數(shù)據(jù)的需求[2]。
作為機(jī)器學(xué)習(xí)研究的新領(lǐng)域,深度學(xué)習(xí)建立了一個(gè)可以模擬人腦進(jìn)行分析學(xué)習(xí)的神經(jīng)網(wǎng)絡(luò),在語(yǔ)音識(shí)別、計(jì)算機(jī)視覺(jué)、自然語(yǔ)言處理等方面得到廣泛應(yīng)用[8]。同時(shí)深度學(xué)習(xí)產(chǎn)生了若干分支,包括自動(dòng)編碼器、深度信念網(wǎng)絡(luò)、卷積神經(jīng)網(wǎng)絡(luò)以及深度玻爾茲曼機(jī)等,在空間數(shù)據(jù)重建領(lǐng)域有著重要的應(yīng)用,但這些方法存在數(shù)據(jù)收集和標(biāo)記的成本過(guò)高、數(shù)據(jù)收集困難等問(wèn)題[9]。生成對(duì)抗性網(wǎng)絡(luò)(Generative Adversarial Network,GAN)[10]也是深度學(xué)習(xí)的一種流行方法。GAN是一種讓兩個(gè)神經(jīng)網(wǎng)絡(luò)相互博弈的非監(jiān)督學(xué)習(xí)方法,它包含一個(gè)生成網(wǎng)絡(luò)G(Generator)和一個(gè)判別網(wǎng)絡(luò)D(Discrim inator)。生成網(wǎng)絡(luò)G的思想是將一個(gè)噪聲映射成一個(gè)逼真的樣本,而判別網(wǎng)絡(luò)D需要判斷生成的樣本是真還是假,GAN通過(guò)G和D的對(duì)峙來(lái)產(chǎn)生G的新框架。
相對(duì)于基于統(tǒng)計(jì)學(xué)方法的MPS方法通過(guò)捕獲訓(xùn)練圖像特征來(lái)完成圖像重建,GAN能夠利用多層神經(jīng)網(wǎng)絡(luò)對(duì)訓(xùn)練圖像進(jìn)行學(xué)習(xí),自動(dòng)獲取抽象的特征,生成與真實(shí)數(shù)據(jù)分布一致的圖像[11]。然而,應(yīng)用于空間數(shù)據(jù)重建領(lǐng)域的GAN方法大多數(shù)都是在大型數(shù)據(jù)集上進(jìn)行訓(xùn)練的[12-14],這對(duì)數(shù)據(jù)集提出了嚴(yán)苛的要求,必然對(duì)訓(xùn)練數(shù)據(jù)不易獲取的任務(wù)造成困難,并且導(dǎo)致訓(xùn)練任務(wù)繁重,對(duì)訓(xùn)練環(huán)境的硬件要求較高。在某些情況下,最好是在少量圖像上訓(xùn)練生成模型,或者在有限的情況下,在單個(gè)圖像上訓(xùn)練。由于單幅圖像中切片的經(jīng)驗(yàn)熵小于圖像分布中切片的經(jīng)驗(yàn)熵,因此學(xué)習(xí)單幅圖像中切片的統(tǒng)計(jì)和分布能夠提供較好的先驗(yàn)知識(shí)[15]。最近的研究也表明,通過(guò)自監(jiān)督學(xué)習(xí)和數(shù)據(jù)增強(qiáng),在單幅圖像上訓(xùn)練一個(gè)模型可以學(xué)習(xí)到足夠的特征信息[16]。但是GAN的感受野有限,因此能夠提取的圖像特征范圍也受到一定限制。如果能夠提取單幅訓(xùn)練圖像在不同尺度或不同分辨率情況下的特征,利用多個(gè)特征進(jìn)行圖像重建,將能夠獲得更好的圖像重建結(jié)果。因此,本文提出一種基于多分辨率GAN的空間數(shù)據(jù)重建方法(稱之為MultiGAN)。
MultiGAN的目標(biāo)是建立一個(gè)能捕捉到不同分辨率下空間數(shù)據(jù)特征的生成模型。為了充分捕捉訓(xùn)練圖像的結(jié)構(gòu)信息,MultiGAN構(gòu)建了一個(gè)金字塔結(jié)構(gòu),該金字塔結(jié)構(gòu)是不同分辨率的訓(xùn)練圖像形成的GAN,每個(gè)GAN在相應(yīng)的分辨率尺度上學(xué)習(xí)訓(xùn)練圖像的結(jié)構(gòu)信息,即在高分辨率訓(xùn)練圖像上捕捉全局特征,在低分辨率訓(xùn)練圖像上捕捉局部特征和細(xì)節(jié)。實(shí)驗(yàn)結(jié)果表明,相對(duì)于普通的GAN模型,MultiGAN可以從單個(gè)訓(xùn)練圖像中產(chǎn)生高質(zhì)量的重建圖像,并且重建時(shí)間較短,因此具有較高的重建效率。
1 本文方法的基本原理
1.1 網(wǎng)絡(luò)模型
本文模型是GAN的一個(gè)變體。其中,GAN是一種非監(jiān)督學(xué)習(xí)網(wǎng)絡(luò),包含相互博弈的兩個(gè)神經(jīng)網(wǎng)絡(luò):生成器G和判別器D。G和D這兩個(gè)網(wǎng)絡(luò)相互作用并不斷調(diào)整,最終目標(biāo)是使判別器無(wú)法判斷生成器的輸出是否是真實(shí)樣本,從而實(shí)現(xiàn)模型學(xué)習(xí)到訓(xùn)練圖像特征的目的。
生成器G和判別器D之間的博弈是由GAN的最小成本函數(shù)決定的:
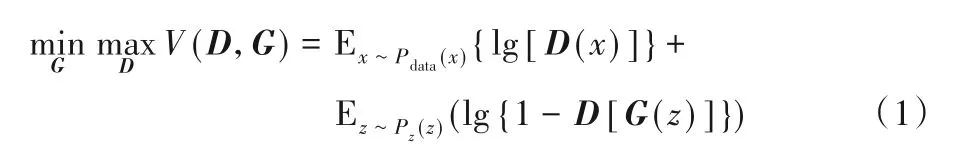
其中,D(x)指的是x來(lái)自真實(shí)數(shù)據(jù)分布Pdata(x)的概率,而D[G(z)]指的是假樣本G(z)產(chǎn)生的概率,E代表期望值。在實(shí)際應(yīng)用中,GAN有時(shí)出現(xiàn)訓(xùn)練較為困難、生成器和判別器的損失無(wú)法指導(dǎo)訓(xùn)練過(guò)程以及生成的樣本缺乏多樣性等問(wèn)題[17],因此出現(xiàn)了一些GAN變體去改善這些問(wèn)題,例如文獻(xiàn)[17-18]從理論和實(shí)驗(yàn)兩個(gè)方面分析了GAN,并對(duì)其進(jìn)行了改進(jìn),提出了WGAN(Wasserstein GAN)。WGAN通過(guò)權(quán)重剪切獨(dú)立地限制每一個(gè)網(wǎng)絡(luò)參數(shù)的取值范圍,確保訓(xùn)練過(guò)程中判別器參數(shù)有界,不會(huì)因?yàn)闃颖镜牟煌o出差別巨大的分?jǐn)?shù)值。但是實(shí)踐過(guò)程中發(fā)現(xiàn),WGAN的權(quán)重剪切的閾值很難設(shè)置合理,設(shè)置較小容易導(dǎo)致梯度消失,設(shè)置較大會(huì)導(dǎo)致梯度爆炸。因此文獻(xiàn)[19]提出WGAN-GP(WGANwith Gradient Penalty),通過(guò)在判別器的損失函數(shù)中加入梯度懲罰項(xiàng)來(lái)改善WGAN的問(wèn)題。WGAN-GP的目標(biāo)函數(shù)為:

1.2 多尺度多分辨率結(jié)構(gòu)
由于受計(jì)算資源和網(wǎng)絡(luò)結(jié)構(gòu)的約束,網(wǎng)絡(luò)的感受野有限,如果直接對(duì)訓(xùn)練圖像進(jìn)行訓(xùn)練,重建后的圖像實(shí)際上只重建了訓(xùn)練圖像上有限大小的結(jié)構(gòu)特征,難以兼顧全局和局部特征,因此本文提出在多種分辨率情況下通過(guò)固定大小的感受野來(lái)掃描不同分辨率的訓(xùn)練圖像,以實(shí)現(xiàn)訓(xùn)練圖像不同尺度特征的提取。將訓(xùn)練圖像按不同的尺度進(jìn)行縮放,形成多分辨率訓(xùn)練圖像用于階段訓(xùn)練,利用固定大小的感受野來(lái)捕獲不同分辨率下訓(xùn)練圖像的結(jié)構(gòu)信息。圖1所示為捕獲不同分辨率的訓(xùn)練圖像信息示意圖,圖中顯示了3個(gè)尺度的訓(xùn)練圖像。
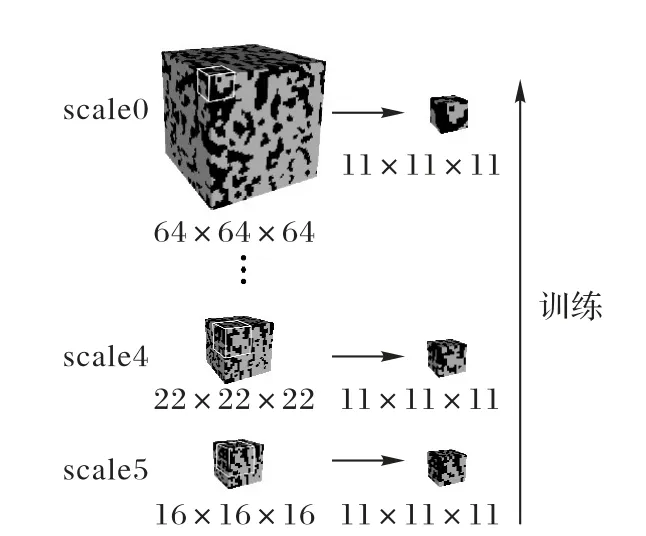
圖1 提取不同分辨率訓(xùn)練圖像信息的示意圖Fig.1 Schematic diagram for extracting training image information at different resolutions
從圖1可以看出,在低分辨率的情況下,模型主要學(xué)習(xí)圖像的整體分布信息;而在高分辨率的情況下,能夠重點(diǎn)學(xué)習(xí)圖像的細(xì)節(jié)和紋理信息。不同分辨率訓(xùn)練圖像的大小為:
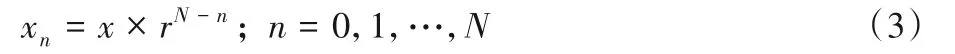
x為輸入圖像大小,N為尺度數(shù)量,r為尺度縮放因子,表示為:
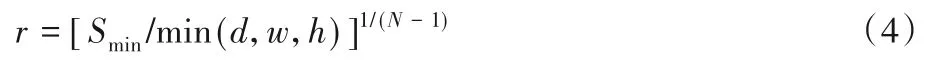
其中:Smin為設(shè)置的最低分辨率下訓(xùn)練圖像的大小,d、w和h分別為輸入圖像x的深度、寬度和高度大小,min(d,w,h)為輸入圖像3個(gè)維度大小的最小值。利用尺度縮放因子對(duì)輸入圖像進(jìn)行下采樣獲得不同分辨率的訓(xùn)練圖像進(jìn)行訓(xùn)練,這一多分辨率結(jié)構(gòu)稱之為“金字塔結(jié)構(gòu)”,圖2所示為N+1尺度的金字塔結(jié)構(gòu)。
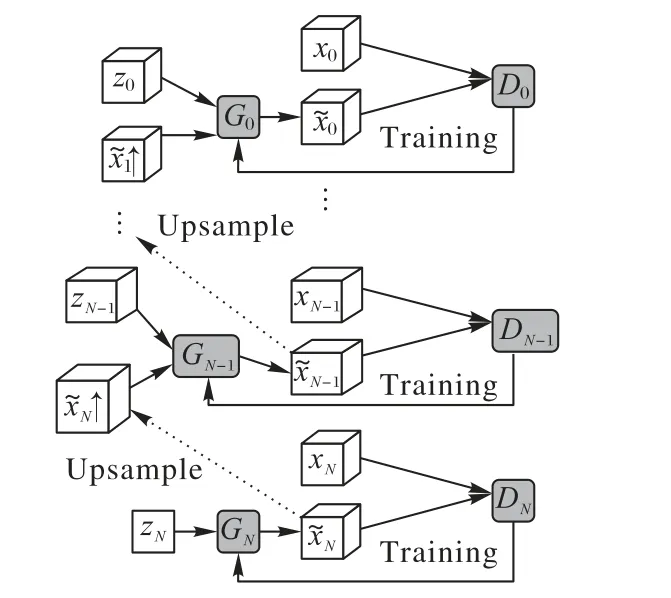
圖2 N+1尺度的金字塔結(jié)構(gòu)Fig.2 Structureof pyramid with N+1 scales
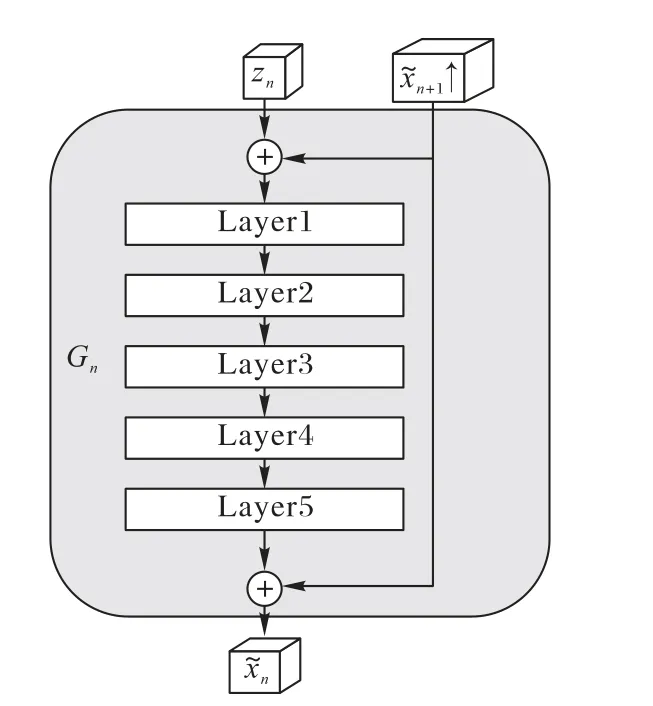
圖3 Gn的結(jié)構(gòu)(0≤n≤N-1)Fig.3 Structureof Gn(0≤n≤N-1)
1.3 模型訓(xùn)練
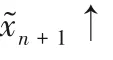
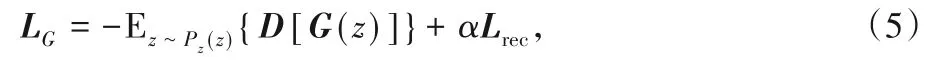
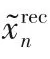

訓(xùn)練過(guò)程中發(fā)現(xiàn),過(guò)高的學(xué)習(xí)率會(huì)導(dǎo)致圖像的過(guò)度擬合和模式崩潰,而過(guò)小的學(xué)習(xí)率則會(huì)導(dǎo)致生成的圖像紋理細(xì)節(jié)不明顯。為了平衡學(xué)習(xí)率與重建圖像效果,模型使用Adam優(yōu)化器[20]來(lái)調(diào)整超參數(shù)。Adam優(yōu)化器不僅可以計(jì)算出各參數(shù)的自適應(yīng)學(xué)習(xí)率,還可以通過(guò)訓(xùn)練數(shù)據(jù)的不斷迭代使網(wǎng)絡(luò)權(quán)重自動(dòng)更新,保證了訓(xùn)練的效率以及重建圖像的質(zhì)量。
2 實(shí)驗(yàn)結(jié)果
為了評(píng)估重建空間數(shù)據(jù)的效果,選擇與MPS方法中SNESIM、FILTERSIM和DS三種代表性算法以及應(yīng)用于空間數(shù)據(jù)重建的GAN[13]方法進(jìn)行對(duì)比,對(duì)重建圖像的變差函數(shù)、孔隙度、多點(diǎn)連接性、CPU、GPU和內(nèi)存使用情況等方面進(jìn)行對(duì)比分析。MultiGAN模型使用五層網(wǎng)絡(luò),金字塔結(jié)構(gòu)為6層,訓(xùn)練圖像大小由小到大為:16×16×16、22×22×22、28×28×28、37×37×37、49×49×49、64×64×64。卷積核大小為3×3×3,感受野大小為11×11×11,激活函數(shù)LeakyReLU的負(fù)數(shù)部分斜率為0.2。
2.1 重建圖像的比較
本實(shí)驗(yàn)擬采用真實(shí)巖石數(shù)據(jù)作為空間數(shù)據(jù)重建的數(shù)據(jù)源,由于真實(shí)巖石的內(nèi)部孔隙數(shù)據(jù)難以用數(shù)學(xué)公式或者某種定量的語(yǔ)句描述,故巖石的孔隙分布具有很強(qiáng)的不確定性特征,適合采用不確定性重建方法重建孔隙結(jié)構(gòu)。使用納米CT掃描技術(shù)獲取分辨率為64 nm/體素的真實(shí)頁(yè)巖體數(shù)據(jù)。從真實(shí)頁(yè)巖數(shù)據(jù)截取尺寸為64×64×64體素的立方體作為訓(xùn)練圖像,其外表面、剖面圖(X=32,Y=32,Z=32)以及孔隙結(jié)構(gòu)如圖4(a)所示。圖4中的頁(yè)巖數(shù)據(jù)由骨架和孔隙兩部分組成,其中灰色區(qū)域代表骨架,黑色區(qū)域代表孔隙空間。從圖4(a)可以看出,訓(xùn)練圖像的孔隙呈現(xiàn)不規(guī)則且長(zhǎng)連通的特點(diǎn)。圖4還顯示了使用SNESIM、FILTERSIM、DS、GAN以及MultiGAN方法重建的圖像。可以看出,五種重建方法均基本再現(xiàn)了訓(xùn)練圖像不規(guī)則且長(zhǎng)連通性的孔隙空間,但是MultiGAN重建圖像與訓(xùn)練圖像最為接近。

圖4 訓(xùn)練圖像和不同方法重建圖像的外表面、剖面圖以及孔隙結(jié)構(gòu)Fig.4 Outside surface,profile and pore structures of training image and images reconstructed by different methods
2.2 孔隙度對(duì)比
巖石孔隙度被定義為孔隙體積V與巖石總體積Vp的比值,用于表示巖石存儲(chǔ)流體的能力,用符號(hào)?表示,定義為:

訓(xùn)練圖像的孔隙度為0.228 2,分別利用SNESIM、FILTERSIM、DS、GAN以及MultiGAN重建10幅圖像,孔隙度結(jié)果如表1所示。從表1可以看出,MultiGAN重建圖像的孔隙度更接近訓(xùn)練圖像孔隙度。
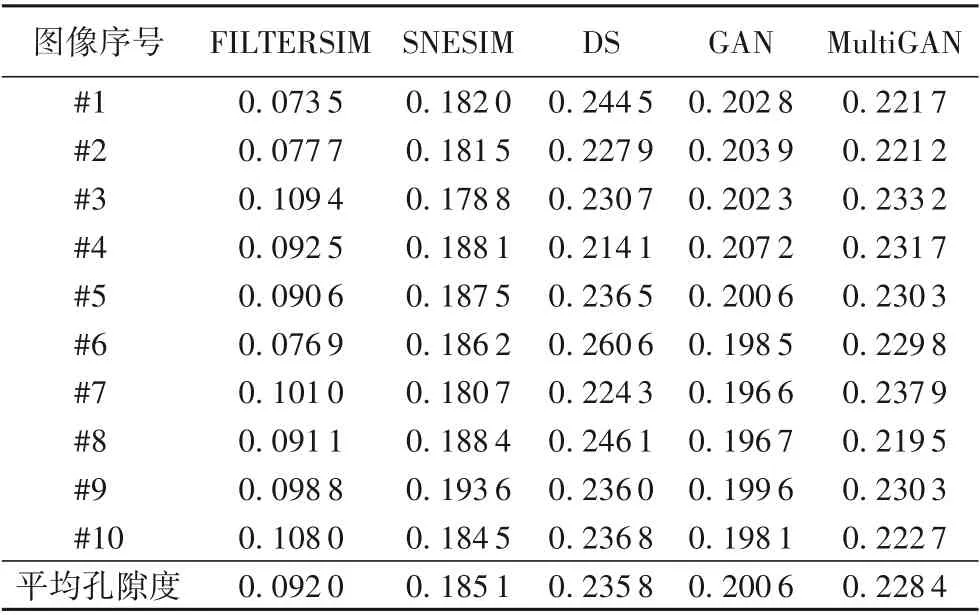
表1 SNESIM、FILTERSIM、DS、GAN和MultiGAN重建10幅圖像的孔隙度Tab.1 Porositiesof 10 images reconstructed by SNESIM,F(xiàn)ILTERSIM,DS,GAN and MultiGAN
2.3 變差函數(shù)對(duì)比
變差函數(shù)反映了在一定方向上的空間變量的相關(guān)性和變異性,常用來(lái)作為評(píng)估重建效果的工具,定義如下:
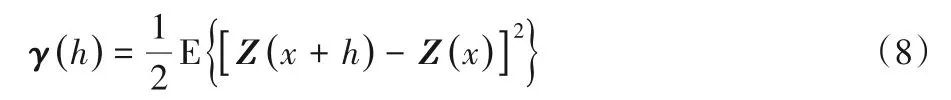
其中Z(x)是位置x處的屬性值,h是位置x和x+h之間的滯后距離,E是數(shù)學(xué)期望值。如果兩幅圖像在同一方向上有相近的變差函數(shù)曲線,則兩幅圖像在該方向上具有相近的結(jié)構(gòu)特征;反之,兩幅圖像在該方向上結(jié)構(gòu)差異較大。圖5是訓(xùn)練圖像和SNESIM、FILTERSIM、DS、GAN以及MultiGAN方法重建圖像的變差函數(shù)曲線。橫軸表示滯后距離,相鄰體素之間的距離為1,縱軸分別表示3個(gè)方向的變差函數(shù)值。
從圖5中可以看出,MultiGAN重建圖像與訓(xùn)練圖像的變差函數(shù)曲線更接近,說(shuō)明MultiGAN重建效果更好。
2.4 多點(diǎn)連接性對(duì)比
變差函數(shù)可以衡量空間兩點(diǎn)間的變異性,為了同時(shí)衡量空間多點(diǎn)之間的連接性,可以定義如下的多點(diǎn)連接性函數(shù)(Multiple-Point Connectivity,MPC):
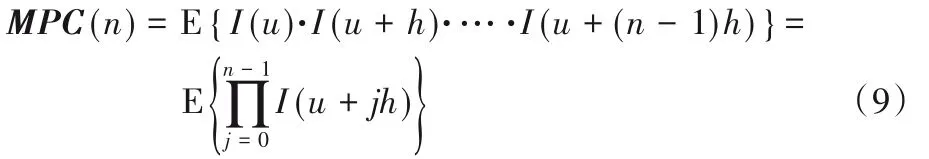
其中:h為滯后距離,n為一個(gè)方向上的節(jié)點(diǎn)數(shù),E為數(shù)學(xué)期望值,u表示空間某點(diǎn)位置。指標(biāo)變量I(u)具有兩個(gè)屬性值:當(dāng)頁(yè)巖圖像中某個(gè)位置為孔隙空間時(shí),I(u)=1;否則I(u)=0。
圖6是訓(xùn)練圖像和使用SNESIM、FILTERSIM、DS、GAN以及MultiGAN方法重建圖像的MPC曲線圖。從圖6中可以看出,MultiGAN方法重建圖像與訓(xùn)練圖像的MPC曲線最接近。
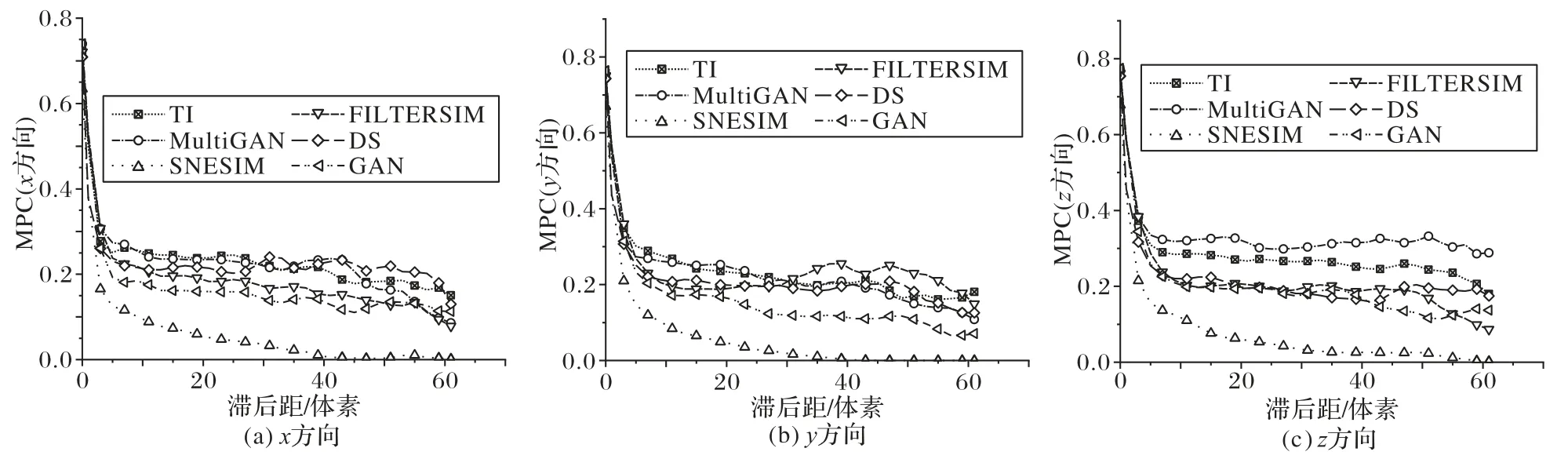
圖6 重建圖像和訓(xùn)練圖像的MPC曲線Fig.6 MPC curvesof training imageand reconstructed images
2.5 內(nèi)存和運(yùn)行時(shí)間對(duì)比
實(shí)驗(yàn)硬件環(huán)境為Intel Core i7-7800X CPU、NVIDIA GeForce RTX 2080 Ti GPU和24 GBRAM。另外,本文的GAN和MultiGAN基于PyTorch的深度學(xué)習(xí)框架運(yùn)行。SNESIM、FILTERSIM和DS使用了基于MPS的軟件框架運(yùn)行。對(duì)SNESIM、FILTERSIM、DS、GAN和MultiGAN算法在CPU/GPU/占用內(nèi)存方面進(jìn)行比較。為了獲得較為客觀的數(shù)據(jù),根據(jù)10次重建的重建結(jié)果進(jìn)行比較,結(jié)果如表2所示。總重建時(shí)間在表2由兩部分組成:第一次重建時(shí)間和其余九次重建總時(shí)間。可以看出,盡管在“第一次重建時(shí)間”項(xiàng)中,SNESIM,F(xiàn)ILTERSIM和DS所花費(fèi)的時(shí)間少于GAN和MultiGAN,但它們?cè)凇捌溆嗑糯沃亟倳r(shí)間”中卻花費(fèi)了更多時(shí)間。這是由于SNESIM、FILTERSIM和DS三種方法每次重建時(shí)都需要重新對(duì)訓(xùn)練圖像進(jìn)行掃描以獲取其結(jié)構(gòu)信息,這些信息存儲(chǔ)在內(nèi)存中而不是文件內(nèi),一次重建結(jié)束后上述結(jié)構(gòu)信息即被清除,而且即使能夠?qū)⑦@些信息存儲(chǔ)在文件內(nèi),整個(gè)重建過(guò)程也會(huì)因?yàn)榇鎯?chǔ)結(jié)構(gòu)非常龐雜而耗時(shí)較長(zhǎng);而GAN和MultiGAN在第一次重建后會(huì)將訓(xùn)練好的模型參數(shù)保存到文件中,而且參數(shù)儲(chǔ)存結(jié)構(gòu)相對(duì)簡(jiǎn)便,因此比傳統(tǒng)MPS方法重建用時(shí)少。對(duì)比GAN和MultiGAN,可以看出MultiGAN在重建效率上優(yōu)于GAN。可見(jiàn),如果MultiGAN在后繼重建過(guò)程中重復(fù)利用第一次重建后保存的模型參數(shù),將對(duì)后繼重建有很好的加速作用,因此比經(jīng)典的不確定性插值方法具有更好的應(yīng)用前景。同時(shí),MultiGAN具有更低的CPU使用率,原因是深度學(xué)習(xí)及其相關(guān)算法的快速發(fā)展,使得MultiGAN等可以結(jié)合使用CPU和GPU,提升了GPU利用效率,降低了CPU的工作負(fù)載。盡管MultiGAN內(nèi)存峰值較高,但是隨著計(jì)算機(jī)硬件的發(fā)展,這樣的內(nèi)存峰值不會(huì)造成較大的問(wèn)題。

表2 不同重建方法的CPU使用、占用內(nèi)存峰值、總運(yùn)行時(shí)間比較Tab.2 Comparisonsof CPU usage,memory peak usageand total running timeof different reconstruction methods
3 結(jié)語(yǔ)
本文提出了一種基于多分辨率GAN的空間數(shù)據(jù)不確定性重建方法,該方法以真實(shí)的空間數(shù)據(jù)作為訓(xùn)練數(shù)據(jù),通過(guò)金字塔結(jié)構(gòu)學(xué)習(xí)訓(xùn)練數(shù)據(jù)的全局和局部特征。訓(xùn)練結(jié)束后的模型可以保存下來(lái),便于之后直接輸入噪聲進(jìn)行重建。目前,一些不確定性插值方法被廣泛應(yīng)用于空間數(shù)據(jù)的重建。例如,使用MPS可以進(jìn)行空間數(shù)據(jù)重建中的油藏模擬,但是時(shí)間較長(zhǎng),效率較低;利用流形學(xué)習(xí)進(jìn)行空間數(shù)據(jù)模擬本質(zhì)上是對(duì)數(shù)據(jù)進(jìn)行降維,不能從根本上減少對(duì)空間訓(xùn)練數(shù)據(jù)的需求;一些其他深度學(xué)習(xí)方法可用于空間數(shù)據(jù)模擬,但是需要大量的空間數(shù)據(jù)訓(xùn)練集,因此適用性受限。而本文使用單幅訓(xùn)練圖像創(chuàng)建的多分辨率結(jié)構(gòu)可以在使用少量訓(xùn)練數(shù)據(jù)的情況下完成重建。
實(shí)驗(yàn)結(jié)果表明,與一些經(jīng)典不確定性插值方法相比,該方法在運(yùn)行效率上表現(xiàn)更優(yōu),并且重建圖像質(zhì)量更高。與GAN方法相比,MultiGAN只需要很少的訓(xùn)練數(shù)據(jù)即單個(gè)訓(xùn)練圖像,而同類GAN方法需要大量訓(xùn)練圖像作為訓(xùn)練數(shù)據(jù),實(shí)驗(yàn)結(jié)果顯示了本文方法在重建效率和質(zhì)量上更優(yōu)。

