大數據背景下VI理論研究與實際應用

季艷秋，盧志義

(天津商業大學 理學院，天津 300134)

1 引言

貝葉斯推斷是統計學習理論的重要組成部分。貝葉斯推斷是從變量的先驗分布出發，利用觀察到的樣本信息，根據貝葉斯公式得到參數的后驗分布，從而對變量及其不確定性進行推斷，進而做出決策的統計方法。貝葉斯推斷在參數估計、模型評價與選擇、概率隱變量建模等諸多統計學和機器學習領域具有廣泛的應用。

在大數據背景下，貝葉斯機器學習通常采用概率隱變量模型，隱變量是模型中一些無法觀測到的變量，它們雖然也是模型的一部分，但由于沒有觀測值，給貝葉斯后驗分布的計算帶來很大的不便。傳統的做法是通過對所有隱變量進行求和或積分運算，從模型中“刪去”隱變量，從而達到簡化計算的目的。但對于復雜模型和大規模數據，以上方法面臨嚴峻的挑戰。主要表現在，由于模型中隱變量較多，可能達到數百萬甚至數億，對這些隱變量進行求和或積分運算顯然是不可行的，即便可以依賴于現代計算機快速計算能力進行精確計算，但計算所消耗的時間代價是無法承受的。在這種情況下，變分推斷(Varational Inference，以下簡稱VI)為貝葉斯推斷提供了一種非常高效的近似替代算法。

設觀測變量x和隱變量z的聯合概率分布p(x,z)，此處的z包括模型的參數。貝葉斯推斷的主要目標是計算隱變量z的條件密度函數p(z|x)，但該密度函數的顯式表達是很難得到的。解決這一問題的方法可分為兩類，即MCMC(Markov Chain Monte Carlo)方法和VI。MCMC抽樣雖然已經成為現代貝葉斯統計不可或缺的工具，但在模型較為復雜或數據規模較大的情形下，MCMC抽樣由于計算量大、收斂速度慢而導致計算成本偏高。VI的思路是在給定觀測變量x的情況下，采用適當的近似方法，得到隱變量z的條件密度p(z|x)在某種意義下的一個近似。與MCMC方法最大的不同是，VI的主要思想不是使用采樣，而是使用優化的思想和方法得到后驗分布的近似。使用變分方法進行近似推斷的優越性在于近似族的選擇具有很大的靈活性，往往能夠較好地接近精確后驗分布，并且近似分布具有計算簡單、穩健性強的優良特性。

VI改變了力求精確建模的傳統認知，是貝葉斯推斷在研究范式上的一種轉變。特別是在大數據背景下，VI為貝葉斯推斷提供了一種相對簡單，但精確度和穩健性都能得到保證的新方法。近20年來，隨著計算機技術的發展和大數據研究的興起，VI愈加受到人們的關注，在許多領域得到廣泛應用且具有良好的效果。然而，對VI的研究和應用主要出現在計算機學科及其應用領域中，并未受到統計學界的重視。本文在回顧VI發展的基礎上，介紹VI的基本理論與算法以及在大數據領域的拓展算法，并對VI在大數據領域的應用與發展前景，以及未來的研究方向進行分析和討論。

2 VI的基本理論

2.1 問題描述

設x={x1,…,xn}為一組數量為n的觀測變量，將模型中所有感興趣的未知變量都看作隱隨機變量，記作z={z1,…,zm}，并設x與z的聯合概率密度為p(x,z)，隱變量的條件密度為p(z|x)。貝葉斯推斷所要解決的問題是根據觀測值以及聯合分布p(x,z)，計算隱變量的條件密度p(z|x)。

由貝葉斯公式，條件密度p(z|x)可通過下式得到：

(1)

式(1)中，分母是觀測數據的邊際密度，也稱為證據(Evidence)。對于許多模型，該積分很難直接計算，或計算的時間成本太高，因此，希望找到一個相對簡單的分布q(z|λ)來近似精確的后驗分布p(z|x)，稱這個近似分布為變分分布，其中λ={λ1，…,λn}為分布q(z|λ)的參數，稱為變分參數。為簡便，省略變分參數λ，用q(z)來表示變分分布。

2.2 證據下界

為了得到精確后驗分布的候選近似分布，首先需要確定一個候選近似分布的變分分布族Q，其中的每個元素q(z)∈Q都是精確后驗分布的候選近似分布。VI的目標是在某種“距離”下找到最優的候選近似分布q*(z)，使其近似真實后驗分布p(z|x)的效果最好。

衡量近似效果常用的指標為KL散度(KL divergence)，也稱為相對熵或信息增益。分布p(z)和q(z)的KL散度表示為KL(q(z)‖p(z))，其計算公式為：

(2)

KL散度是兩個分布之間接近程度的度量，它是非對稱的，即KL(q(z)‖p(z))≠KL(p(z)‖q(z))，并且是非負的，且當p(z)=q(z)時達到最小值0。

在KL散度下，VI問題轉化為以下優化問題：

(3)

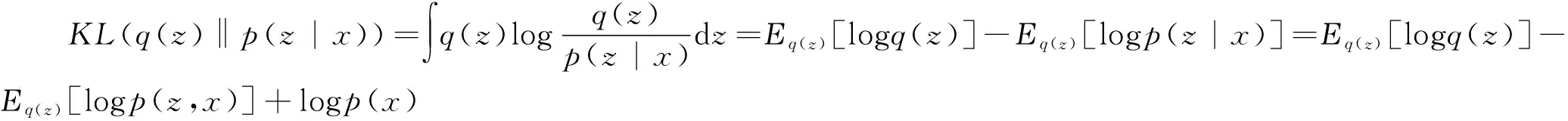
(4)

其中，Εq(z)[·]表示關于q(z)的期望，令

L(q)=Εq(z)[logp(z,x)]-Εq(z)[logq(z)]

(5)

則由(4)可得：

L(q)=logp(x)-KL(q(z)‖p(z|x))

稱L(q)為證據下界(Evidence Lower Bound，以下簡稱ELBO)。對于任意的，由于KL散度是非負的，所以log(x)≥L(q)，即L(q)為對數似然函數(或證據函數)logp(x)的一個下界，這也是“證據下界”名稱的由來。進一步，由(3)和(5)，并注意到logp(x)與q(z)的選取無關，所以最大化ELBO等價于最小化KL散度。

進一步，由(5)式可得：

L(q)=Εq(z)[logp(z,x)]-Εq(z)[logq(z)]=Εq(z)[logp(z)]+Εq(z)[logp(x|z)]-Εq(z)[logq(z)]=Εq(z)[logp(x|z)]-KL(q(z)‖p(z))

(6)

式(6)的第一項是對數似然函數的期望，第二項是變分分布與隱變量先驗分布的KL散度。為了使證據下界達到最大，對數似然需達到最大，而變分分布與先驗分布盡量接近。所以ELBO體現了傳統貝葉斯統計的基本思想，即似然與先驗之間的均衡。因此，在VI中，常采用ELBO作為目標函數來尋找最優的變分分布，因而，問題(3)的求解轉化為以下最優化問題：

(7)

2.3 平均場VI理論

候選分布族的復雜性決定了VI中優化問題的復雜性，Q的不同選取方法會產生不同的VI理論和方法。最早也是最常用的VI理論是平均場VI(Mean-Field Varational Inference，以下簡稱MFVI)。在MFVI中，假定隱變量之間是相互獨立的。獨立性的假定可以簡化VI的計算及優化過程，因此MFVI在諸多領域得到了廣泛的應用。

平均場變分分布族(記為QMF)中的元素q(z)可以寫成如下形式：

(8)

該形式中，每個隱變量zj都由變分因子q(zj)獨立體現，因此這種結構也稱為完全分解結構，這種結構可以通過簡單的迭代更新來優化變分下界L(q)。

將(8)式代入(5)式，并利用變量間的獨立性(即平均場假設)分解(5)式的第二項，同時，將與q(zj)無關的項作為常數項(記為cj)，可得到q(zj)的變分下界L(qj)的表達式：

Εq(zj)[Εq(z-j)[logp(zj,x|z-j)]]-Εq(zj)[logq(zj)]+cj=-KL(logq(zj)‖Εq(z-j)[logp(zj,x|z-j)])+cj

(9)

其中，z-j表示隱變量z中除去zj剩下的變量，Εq(z-j)[·]表示關于q(z-j)的期望。

由KL散度的定義及(9)式可知，問題(7)的最優解q(zj)為:

logq*(zj)=Εqz-j[logp(zj|z-j,x)])+c

(10)

其中，c為與優化無關的常數，對這個結果求冪并歸一化得到:

q*(zj)∝exp(Εqz-j[logp(zj|z-j,x)])∝exp(Εqz-j[logp(x,z)])

(11)

以上優化VI的方法稱為坐標上升VI算法(Coordinate Ascent Variational Inference，以下簡稱CAVI)。

3 VI的研究進展

20世紀80年代，Peter和Hinton等開始研究VI，并將此方法應用于神經網絡中，以得到貝葉斯推斷中后驗概率分布的近似。1988年，Parisi[1]提出了平均場理論，將VI的部分統計特性與期望最大化算法相結合，使VI方法更具普適性，從而推動了VI的發展。之后，Hinton和Van Camp等在1993年提出了一種類似于神經網絡模型的變分算法[2]，吸引了愈來愈多的學者在不同模型中應用VI算法。進入21世紀，隨著計算技術的發展以及數據復雜性的增強，VI方法得到了迅速發展。下面從理論研究和實際應用兩方面闡述VI的最新研究進展。

目前，在理論研究方面，VI方法的最新研究可以概括為以下四個方向。

在VI的準確性方面，變分分布的復雜性與推斷的準確性始終是一對矛盾，因此在可承受的計算成本下，盡量提高推斷的準確性，是VI研究的突破方向。Barber等[3]提出可積分的VI方法，提升了VI的計算準確度和速度； Mimno等[4]提出hybrid VI方法，提高了傳統VI的性能；Huggins等[5]提出了VI中后驗均值和不確定性估計誤差的界限，提高了近似的準確性等。

為了提升VI方法處理大規模數據集時的效率，Hoffman等[6]提出隨機VI方法(Stochastic Varational Inference，以下簡稱SVI) 。在每次迭代中，SVI方法只需要使用少量的樣本計算目標函數的無偏梯度，就能在保證準確性的同時實現VI的快速優化；之后，一些研究進一步改進了SVI算法，如Ranganath等[7]在2013年提出具有自適應學習率的SVI方法，加快了SVI方法的收斂速度，又在2016年提出算子變分推理，允許推斷擴展到海量數據；2020年，Tomczak 等利用一種新的再參數化技巧，提高了在大規模網絡結構上使用VI方法的性能。

在實現VI的通用框架方面，Ranganath等[8]在2014年提出黑盒VI方法，該方法可在模型結構未知的情況下推導出梯度或進行分區函數評估；之后，Titsias等[9]在2015年提出一個關于隨機VI的黑盒方法；2019年，Ruiz等在黑盒VI的基礎上，使用重要性采樣方法減小蒙特卡洛梯度的方差。這些方法使得非專業人士也能輕松的使用VI方法。

在放寬VI的獨立性假設方面，為了考慮變量之間的相關性，并使目標函數可解，許多學者對此進行了大量的研究。Opper等在2009年提出了高斯推理方法；Hoffman等在2015年提出結構化的VI方法；同年，Han等提出高斯copula VI方法；Tran等在2016年提出copula VI[10]，等等。

在大數據背景下，得益于快速發展的計算技術以及便捷的統計計算軟件，VI方法與各種統計模型相結合，被廣泛于應用于各個領域，下面介紹代表性的應用成果。

在計算生物學方面，VI已被用于全基因組關聯研究；調解網絡分析、基因序列檢測、系統發育隱馬爾可夫模型、種群遺傳學以及基因表達分析等。

在計算機視覺和機器人領域，VI所具有的能夠快速推斷的特性在視覺系統中起著重要作用。最早的例子包括推斷非線性圖像流形和在視頻中尋找圖像層。最近，VI在圖像去噪、機器人位置識別和映射、以及圖像分割[20]等方面的應用中也有很大的突破。

在計算神經科學方面： VI有著廣泛的應用，包括多學科層次模型、空間模型、腦機接口以及因子模型，等等。特別是，該領域的研究人員還研發出了一個使用變分方法解決神經科學和心理學研究問題的軟件工具箱。

在自然語言處理和語音識別方面：VI已被用于解決解析語義、語法歸納、流文本模型；主題建模、隱馬爾可夫模型和詞性標注等問題。在語音識別中，VI被用來擬合復雜耦合的隱馬爾可夫模型等。

VI還有許多其他的應用。包括市場營銷、強化學習、統計網絡分析、天體物理學和社會科學等，并且，開發了各種類型的模型，如收縮模型、一般時間序列模型、穩健模型和高斯過程模型等等。

4 大數據背景下VI的拓展：SVI

經典的平均場VI在歷史上一直發揮著重要作用。然而，在大數據背景下，經典VI算法的計算量會變得非常龐大。即便是上文所述的坐標上升VI算法，隨著數據量的增長，每次迭代的計算量也會大幅增加，影響了其在大數據處理中的應用。Hoffman等提出的SVI算法，在每次迭代中采用少量的樣本就可以得到目標函數的無偏梯度，可以大幅減少計算量，因而適宜于大規模數據情形下的VI。

指數族分布是貝葉斯統計和機器學習中經常用到的一類統計模型，指數族模型中常見的是由參數和隱變量組成的條件共軛模型，本文以條件共軛模型為例介紹SVI算法的基本思想。

4.1 條件共軛模型

考慮上文中的條件共軛模型，設β為模型參數，則模型所有變量的聯合概率密度為：

(12)

為了確保式(12)中的聯合概率密度服從指數族分布，首先假設以β為條件的每對(xi,zi)的聯合密度函數具有指數族分布的形式:

p(zi,xi|β)=h(zi,xi)exp{βTt(zi,xi)-a(β)}

(13)

這里t(·，·)的是該分布的充分統計量。同時，假設參數的先驗分布就是相應的共軛先驗：

p(β)=h(β)exp{αT[β,-a(β)]-a(α)}

(14)

這里假設參數的先驗分布具有自然(超)參數α=[α1,α2]T，α為一列向量，并且為充分統計量。使用共軛先驗，可以使式(12)中的聯合概率密度服從指數族分布，且自然參數的估計值為[1]：

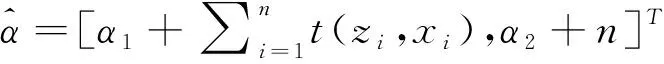
(15)

由式(12)可知，給定β和xi，隱變量zi條件獨立于其他隱變量z-i和其他觀測數據x-i，z-i表示隱變量中除去第i個隱變量以外的變量，x-i表示觀測變量中除去第i個觀測變量以外的變量，于是有：

p(zi|xi,β,z-i,x-i)=p(zi|xi,β)

(16)

由式(13)的局部似然項p(zi,xi|β)的性質，進一步假定上式的分布為指數族分布，具有形式

p(zi|xi,β)=h(zi)exp{η(β,xi)Tzi-a(η(β,xi))}

(17)

將以上所定義的模型稱為條件共軛模型。

4.2 條件共軛模型的CAVI算法

上節所描述的條件共軛模型可以采用CAVI算法進行變分推斷。用q(β|λ)表示β的變分后驗近似密度函數，其中，λ為全局變分參數。用q(zi|φi)表示隱變量zi的變分后驗密度函數，其中φ={φ1,φ2,……,φn}為局部變分參數。CAVI通過交替更新局部變分參數和全局變量參數進行迭代，從而優化ELBO，當ELBO的值收斂時，停止迭代。其中局部變分參數的更新公式為：

φi=Ελ[η(β,xi)]

(18)

全局變分參數的更新公式為：

(19)

將(12)中的聯合概率密度以及相應的平均場變分密度代入式(5)，并省略與變分參數無關的項，可得每次迭代中ELBO的計算公式：

(20)

其中，

(21)

4.3 條件共軛模型中ELBO的隨機優化

在基于梯度法的優化問題中，自然梯度以一種可感知的方式扭曲了原有的參數空間，使得在新的空間中，參數在不同方向上的變化量相同時，相應的KL散度的變化量也保持相等，因而采用自然梯度可以提高優化問題的效率。

在指數族模型中，在歐氏梯度的基礎上乘以費雪信息矩陣的逆f(λ)-1可得到參數的自然梯度。Hoffman等得出ELBO的歐氏梯度為[23]:

(22)

從而，可得到自然梯度g(λ)的計算公式為：

(23)

顯然，自然梯度除了具有良好的理論特性外，要比歐氏梯度更容易計算。

若在ELBO的優化中采用自然梯度，全局變分參數的迭代公式可寫成：

λt=λt-1+εtg(λt-1)

(24)

其中εt為步長。將式(23)代入式(24)中，可得：

(25)

式(25)表示在每次迭代中，首先進行坐標更新，然后將當前估計調整為更新后的坐標和前一次迭代中變分參數的值的加權組合。

在計算條件共軛模型的自然梯度時，除了計算坐標上升更新外，不需要其他計算。SVI是利用自然梯度并結合隨機優化算法來解決大數據情形下優化算法的計算復雜性問題的。研究表明，只要步長序列滿足一定的條件，SVI就可以使用有噪聲但無偏的梯度來優化目標函數ELBO，從而使得機器學習方法能夠拓展到大數據領域[24]。

SVI首先構造一個計算成本低、有噪聲、無偏的自然梯度。將(15)代入(23)得到：

(26)

通過從(1,……,n)上的均勻分布中抽取樣t，構造一個有噪聲的自然梯度：

t～Unif(1,……,n)

(27)

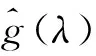
為使以上算法收斂，步長序列需滿足一定條件：

(28)

通過SVI算法，可以在大數據背景下快速優化ELBO，獲得較為準確、穩健的變分近似后驗。

5 總結與展望

VI使用優化方法來近似目標概率分布，其目的并非求出精確概率分布的解析形式，而是找到近似度高、計算相對簡單、穩健性好的近似分布。VI適用于大規模數據集以及希望快速探索大量模型的場景。VI改變了人們精確求解隱變量概率分布的傳統認知，是對經典貝葉斯理論的有益補充。從20世紀八九十年代第一次提出VI方法至今已有30多年歷史，近年來，VI方法得到了快速發展，漸趨成熟。同時，隨著大數據的興起，VI的應用領域也愈加廣泛。本文回顧了VI的發展歷程，介紹了VI的基本原理，并綜述了大數據背景下VI的拓展。

面向未來，VI無論在理論上還是在應用上，仍有許多尚未解決但很有研究空間的問題。作為本文的結束，提出VI未來需要進一步研究的問題和方向。

5.1 開發更好的分布間近似程度的度量指標

本文重點介紹了使用KL散度度量兩個分布之間的近似程度的VI問題。然而KL散度不具有對稱性，這在某種程度上影響了VI的研究與應用。因此開發更好的度量分布間近似程度的指標，是VI在理論研究方面的重要方向之一。

5.2 改進平均場VI中的獨立性假設

雖然平均場VI方法很靈活，在實際中得到了廣泛的應用，但平均場方法是建立在嚴格的獨立性假設的基礎之上的。獨立性假設雖然有助于簡化計算、便于優化，但大大限制了變分分布族的選擇范圍，從而導致低估后驗方差等問題。因此，如何在保持優化方法有效性的同時，考慮不同分量之間的相依性，以得到更好的近似后驗分布，是未來的重要研究方向。

5.3 VI與MCMC結合

VI與MCMC是估計隱變量條件密度的兩種不同方法，一個自然的問題是，能否將兩種方法結合起來，既可以利用MCMC在估計準確性方面的優勢，也能發揮VI在計算成本方面的優勢。近年來，一些文獻對此問題進行了初步的探討。例如，Zhang等將MCMC與VI結合在一起，不僅能準確、有效地逼近后驗圖像，而且有利于進行MCMC和Gibbs采樣過渡的隨機梯度設計；Francisco等[11]通過運行幾個MCMC步驟來改進變分分布，獲得了更好的預測性能。可以預見，在理論上進一步研究VI與MCMC結合的問題，將是未來理論和實踐方面的重要研究課題。

5.4 VI的統計特性

從統計學的視角，對于MCMC，統計學者已對其進行了大量的研究，取得了豐碩的理論成果。但是，鮮有文獻對VI的統計特性進行探索，例如，當用變分分布代替真實后驗分布時所產生的近似誤差大小的度量，以及采用近似分布進行預測時預測誤差的度量問題。因此，從統計學的角度，對VI進行系統而深入的研究是未來的重要研究方向。