巧用幾何直觀策略 提升數學核心素養

林秋明

一、豐富直觀表征，促進有效建模

如何契合學生認知水平，借助生活原型搭建幾何直觀，運用多種圖形表征以正確描述和分析問題，有效建立數學模型，是值得教師不斷思考的問題。

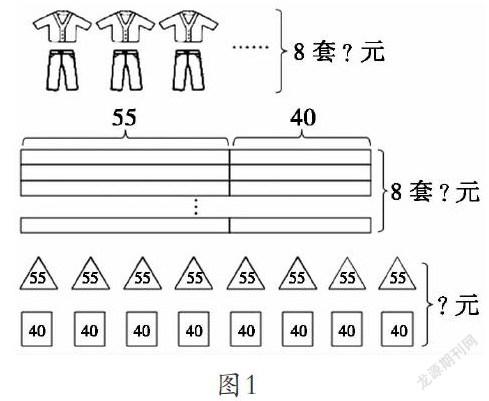
例如，人教版四下“乘法分配律”的教學，教師創設買表演服的情境：學校武術隊購買新的表演服，每件上衣55元，每條長褲40元，買了8套，一共需要多少元？通過引導學生小組合作進行畫圖分析，很快獲得多種直觀表征（圖1）。

在不同的直觀表征中，教師通過遞進式的問題串激發學生進行思考：（1）你能說說示意圖表示什么意思嗎？（2）解決這道題可以有幾種算法？又可以寫成一個什么樣的等式呢？ （3）你能用自己的話說一說這個等式的意思嗎？（4）除了用數字的方法，我們還可以怎么表示這個等式？（用符號或字母表示）（5）哪個等式表述起來更順口？（字母式）這些問題很好地溝通了不同表征之間的內在聯系，促使學生在層層遞進推理中完成乘法分配律這一模型的建構。

二、變換構圖方式，提高解題能力

當學生借助直觀表征解題遭遇瓶頸時，教師要善于把握幾何直觀的優勢進行解決問題分析策略的指導，讓學生在對比辨析中發現知識之間的區別與聯系。通過變換構圖方式，化繁為簡，化難為易，啟迪解題思路，提高學生的思維能力和解決問題的能力。

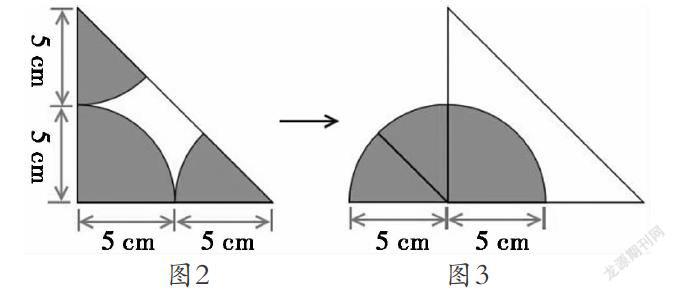
例如，人教版六上“圓”這一單元中關于扇形面積的一道習題（圖2），要求圖中陰影部分的面積，也就是求三個扇形面積之和。剛接觸這種問題，學生往往沒有頭緒，很難把它與之前學過的三角形內角和的探究過程聯系到一起。這時，教師可拋出問題：“這三個扇形有什么特點？你有什么想法？”引導學生觀察發現：大三角形是一個等腰直角三角形，兩個底角都是45°，即三個扇形的圓心角分別是90°、45°、45°，圓心角之和正好是180°，而180°的角是一個平角。由于三個扇形的半徑也相等，因此正好可以拼成一個半圓。通過變換構圖，就可以將問題轉化為“求半徑是5厘米的半圓（圖3）面積”，問題就可以迎刃而解。

三、依托數形結合，加深知識理解

數形結合是一種重要的數學思想方法，其實質在于通過數和形的對應與轉換，使抽象的數學描述與直觀的幾何圖形巧妙地結合在一起。

如教學1+2+3+4+…+n，由于“在n趨于正無窮時，其和沒有極限，題值為無窮大”這知識點對于小學生來說十分深奧，理解起來比較困難。因此，筆者通過化繁為簡，借助邊長是1的小正方形開始研究前四個數相加情況。先擺放從1到4的小正方形個數讓學生觀察，然后將其置于邊長是4的大正方形中，借助圖形，學生不難看出求從1到4的和，其實是可以轉化為求這疊加圖形的面積。為了便于進一步觀察，筆者有意識地添加上一條對角線（圖4），引導學生繼續觀察對角線的斜下方和斜上方兩個陰影部分的面積。學生發現：斜下方是一個大三角形，面積正好是整個大正方形面積的一半，即×4×4;斜上方則是4個小正方形面積的一半，即×4，因此得出：1+2+3+4=×4×4+×4=×4×（4+1）。結果出來后，筆者沒有就此打住，而是繼續出示1+2+3+4+5+6與1+2+3+4+5+6+7+8+9的圖例（圖略），引導學生觀察這兩幅圖中對角線的斜下方和斜上方兩個陰影部分的面積各是怎么計算的。利用知識遷移，學生順利寫出了答案。筆者最后追問：“如果不看圖，繼續寫更多連續自然數的和，你能知道結果等于多少嗎？你能說說它的圖是什么樣的嗎？”通過對多組數列的探究，學生自然就能得出1+2+3+…+n=n（n+1）這個較為抽象的結論了。

四、巧借信息技術，助推思維發展

教師可適時借助信息技術模擬問題情境，化抽象語句為直觀可視的幾何動畫，幫助學生打開思路，優化課堂教學。

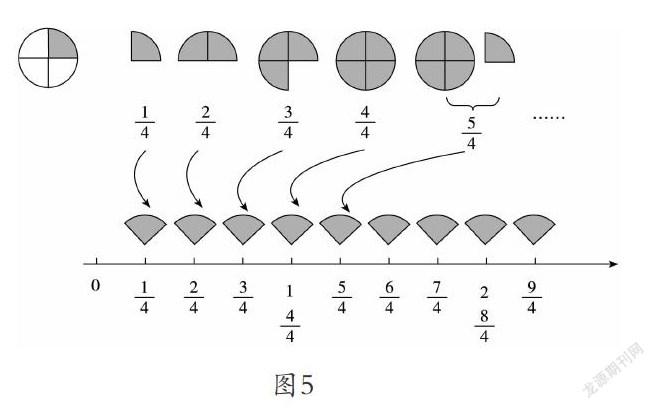
如人教版五下“真分數和假分數”的教學，教師除了可以利用圖形來表示具體的分數之外，還可借助數軸來研究分數，依托信息技術，使圖形所表示的分數與數軸上的點之間建立起聯系。教學中，教師可將若干個相同的圓都平均分成4份，每份用分數表示都是，每添加這樣的1份，分子相應加1，而分母不變;這樣的1份、2份、3份、4份……用分數表示分別是? ……這些都能在數軸上找到相對應的點（圖5）。在這一一對應中，學生獲得明晰的表象信息，從而進一步理解、掌握分數的意義，感受分數的連續性以及分子、分母之間的內在關系，為深入學習真分數與假分數的有關知識做了很好的鋪墊。

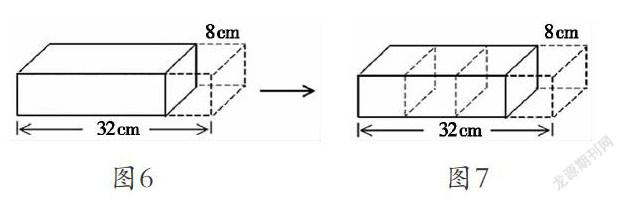
又如，在教學“長方體的體積”時，有這樣一道習題：從一個長32 cm的大長方體上，切下一個長8 cm、體積120 cm■3的小長方體，求原來大長方體的體積。可以利用幾何直觀形象呈現問題（圖6），有了圖示，學生不僅厘清了解題思路，還找到了不同的解題方法。

通過觀察，學生不難看出切割前后長方體的側面積保持不變，從而懂得解題關鍵是先求出這個長方體的側面積，然后再用側面積乘對應的長就能求出原長方體的體積了。當教師繼續借助多媒體技術對示意圖進行進一步的動態切割（圖7），學生茅塞頓開：原來整個長方體的長與切下長方體的長成倍數關系。由此可知這兩個長方體的體積也成倍數關系，于是就有了第三種解法，即：120×4=480（cm3）。

（作者單位：福建省福州市錢塘小學屏北分校）