基于位移的橋梁結構抗震設計

余國平

摘 要：橋梁結構設計影響著橋梁的抗震性能，因此提出基于位移的橋梁結構抗震設計。主要從結構橫梁相互的撞擊、底部橫梁架連接器的作用失效、橋墩破壞三個方面分析橋梁結構的震害，確定抗震設計的最佳需求，并基于位移對橋梁結構進行抗震設計，盡可能的在設計上避免因結構部位的缺陷而在震中導致橋梁出現不可逆轉的損害，避免橋梁位移產生的不確定的影響，通過實驗結果表明，采用改進設計可有效提高橋梁的抗震性。

關鍵詞：橋梁結構;抗震性;位移

通過近年來國內外地震災害的實例，我們可以了解到，要想適應新時期社會發展的要求，人民群眾不光要提高自己的抗震思想，在震中保障生命安全，還需要政府積極采納年輕一代新鮮血液的設計思路，加快提高橋梁抗震設計水平，對已有橋梁進行高頻次抗震實驗，并進行分析與改進，對于我國以及周邊在地震帶上的國家來說，有著重大的研究意義。對此，進行橋梁抗震設計是當前工程界研究的重點。本文以某橋梁為研究對象，建立有限元模型，提出基于位移的橋梁抗震設計方法。

1 橋梁結構主要震害分析

研究橋梁抗震的一個重要內容就是了解橋梁結構的破壞機理及震害形式，從破壞機理和震害形式出發，盡可能地多提出新鮮的抗震設計思路和方法。以地震后的災害模式來看，對于地震對橋梁結構的損害，一般有以下三種情況：

1.1 結構梁相互的撞擊

地震使地殼發生劇烈碰撞，橫波和縱波都會對建筑產生破壞，縱波的產生會導致地面進行上下波動，對橋梁上部結構的損壞不是很嚴重，而往往是因為發生橫波地震的時候，橋柱橫梁之間進行前后移動，連接處產生撞擊，對橫截面產生破壞，導致梁體之間的撞擊愈發嚴重，建筑材料破碎，最終導致主梁破裂并產生坍塌。梁體脫落形式包括順橋向，橫橋向和扭轉滑移;梁體相互碰撞則主要發生在具有伸縮裝置的位置。

1.2 底部橫梁架連接部分的作用失效

在對橋梁抗震設計的分析中，底部橫梁架是抗震設計中尤為重要的地方，而橋梁底部有一個抗震性最差的位置為支座連接器，其連接著梁架伸縮縫，對剪力鍵也有著不可忽視的影響。這個對橋梁進行部位支撐的連接器一旦產生故障會使整個橋梁的傳遞方式的改變，對橋梁其他部位的抗震能力變差，產生十分危險的影響，加劇地震對橋梁建筑的破壞。在以前的地震中，軸承故障很常見，這主要是由于在設計中未充分考慮抗震要求，結構措施（例如結構連接和擋塊）不足以及軸承形式和材料的缺陷。地震作用下的軸承失效將導致結構內力的重新分布，從而導致結構失效甚至坍塌。軸承連接器的主要故障形式是軸承固定螺栓的拔出和縮短，活動軸承的脫落以及軸承的結構故障。

1.3 橋墩破壞

彎曲破壞是指橋墩由于過度彎曲變形而失去承載能力的現象，從而導致混凝土表層剝落，縱向鋼筋屈服，核心混凝土破碎或開裂。彎曲破壞一般都會在橋墩墩底部位或墩頂部位形成塑性鉸，并引起結構內力重分布，吸收部分地震能量，具有較好的延性。如果因為橋墩的抗彎承載力超過地震作用下的抗剪承載力，此時橋墩無法承受過大的壓力，致使橋梁柱產生破裂，一旦橋墩截面壓力過高，其抗剪能力迅速下降，就會使得橋墩結構被分裂，最終導致坍塌。塑性材料鉸鏈成形后，由于抗剪強度突然下降而導致的彎曲破壞效果優于結構破壞效果。

綜上分析震害現象可知，落梁與碰撞破壞、橋墩破壞、支座等連接構件破壞等均會出現位移現象，在對橋梁結構進行抗震設計過程中，在考慮位移對橋梁結構的影響下進行抗震設計。

2 橋梁結構抗震設計

基于位移的橋梁抗震設計方法直接以結構位移為設計指標。 根據不同的地震設防級別，合理地控制結構的整體行為。

2.1 結構損傷分析

在地震作用下，結構的破壞和損傷取決于強度，變形能力和累積能量消耗。破壞指數可以描述為地震引起的結構破壞。選擇時應考慮材料的成分和結構的力學特性，并一起評估地震的破壞控制效果。對于易于發生塑性變形的鋼筋混凝土結構，使用最廣泛的指數可以對橋梁位移架構進行適當性的調整。此時因結構能耗下降，通過基本變形參數和疊加能量吸收線性公式，可計算出位移產生的影響：

式中：位移程度的最大值和閾值用、來表示，而、和則分別表示為結構承受強度、可控效應值，和抗壓損傷絕對值。

累積損傷僅僅是通過能量項來說明，對指標進行優化，接觸彈性變形帶來的干擾，從截面層次計算結構損傷，計算公式為：

式中：代表攔截震波對截面波動的控制的最高曲率，代表預估截面可承受的極限閾值，和表示截面形狀改變的最高角度和抗壓積累值。

2.2 雙自由度橋梁模型

由于摩擦滑動軸承具有非線性特性，且子結構基本上是彈性的，因此可以利用等效剛度和等效阻尼比對非線性結構進行等效分析，從而得到結構的替代響應。以簡化的方式估計橋的非線性行為，將橋簡化為具有兩個自由度的振動系統，并通過動態平衡法獲得每個自由度的運動方程，并將絕對位移坐標轉換為相對位移坐標，最后計算結構目標位移，得出等效阻尼比：

其中，為橋墩阻尼基本參數比值，為墩柱頂端偏移路線，而底部支座阻尼等效比值和支座偏移角度值用和來表示。

可得出第一階模態自振頻率和周期參數，由此可分析各部分等效線性參數為：

根據修正對應的位移反應譜，計算時的結構位移和：

比較和，若誤差大于5%，則需重新迭代計算，若誤差小于5%，計算結束，則。

2.3 基于位移的抗震設計

一般來說，鋼筋混凝土橋墩自有的延展性能力由位置參與構件位移延展性參數來表示，其內容表示為延展性最高值與位移閾值的比值系數，該系數用表示，根據橋墩底部的橫梁結構，將位移分為屈服位移和極限位移，計算墩身曲面率與沿橋墩之間線性比是否為高度線性，假設已知塑性鉸區域長度為，在區域內墩底結構墩柱塑性因位移產生轉動變形，使區域曲率等于當前墩底截面的最高曲率，通過此時位移閾值可計算出區域內因轉動變形產生的位移參數，當轉動變形達到橋墩墩頂延展性參數絕對值并達到極限區域時，其表達方式為：

在橫向地震作用下，如果封頂梁的剛度足夠大，則在多柱墩的頂部和底部可能會出現彎曲的塑料鉸鏈。在此情況下，軸向力動力輸出與塑性鉸機構因雙向運動而對雙柱墩產生相對彈性位移，影響動力軸位移能力比值，可計算出雙向柱墩彈塑性的簡化算法。

式中，墩頂用表示，墩底延展性彎矩用表示，經計算與兩者實際數值和參數相同。

3 實驗驗證

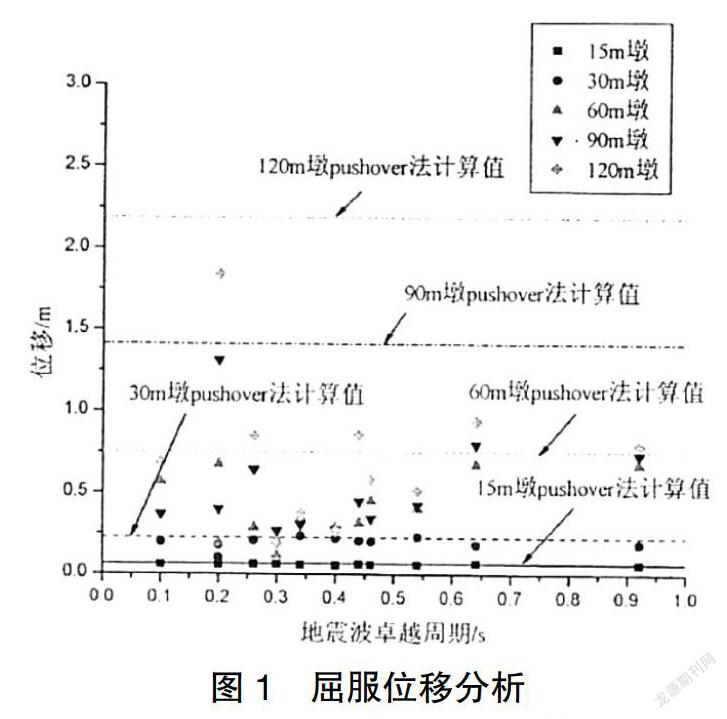
為驗證改進設計的有效性，本文運用ANSYS有限元軟件建立模型，以位移延性能力為對比目標進行有效性驗證，結果如圖1所示。

由圖1和圖2的分析可得出，使用本文分析的方法，普通的15 m橋墩，在不同震波產生的撞擊下，橋墩極限延展性與位移程度無論是計算內容還是預估內容，所得參數幾乎相差很小;超出15 m的橋墩，則預測值與計算結果隨著橋墩高度的增加而加大。由圖2可知，當橋墩高度增大時，極限位移相比預測值較小，在本文論述中，延展性位移參數與極限數值經計算所得，與預測值相比均較小，在橋墩高度增加的情況下，本文論述方法對比較小橋墩，其效果更優。

文中不僅分析了震中橋梁位移對橋梁結構的影響，還提出了如何使橋梁抗震設計避免因墩柱延展性雙向運動產生彈性位移的影響。因此，除15 m墩外的其他墩柱計算結果均小于預測結果。

4 結束語

針對傳統的橋梁抗震設計存在抗震效果差的問題，提出基于位移的橋梁結構抗震設計，在分析位移的基礎上，對橋梁結構進行抗震設計，實驗結果表明，采用改進設計方法可有效提高橋梁抗震效果。

參考文獻：

[1]布占宇，葉晗暉，葛勝良，等.直接基于位移的預制拼裝墩柱抗震設計[J].中國公路學報，2018，31（12）：250-257.

[2]劉忠華，李幗昌，楊志堅，等.基于位移的屈曲約束支撐混凝土框架結構抗震設計方法[J].工業建筑，2017， 47（3）：18-24.

[3]李宇婧，李宏男，李超.基于偏好序的橋梁結構全壽命抗震設計多目標優化模型[J].中國公路學報，2017， 30（12）：187-195.