基于對數行列式實現的矩陣補全算法

秦國峰 彭沖 魏計鵬

摘要：傳統的基于低秩假設的矩陣補全模型常常對目標矩陣采用核范數的約束，由于核范數對秩函數的近似不夠精確，基于核范數的低秩模型可能無法產生最優的效果。為此，采用對數行列式代替核范數，提出基于最小化矩陣對數行列式的矩陣補全模型。研究結果表明，基于最小化對數行列式實現的矩陣補全算法能夠有效地恢復矩陣的低秩信息，能夠有效地補全圖像的缺失信息。

關鍵詞：矩陣補全;低秩結構;對數行列式;機器學習

中圖分類號：TP181

文獻標志碼：A

收稿日期：2020-11-06

通信作者：彭沖，男，博士，副教授，主要研究方向為機器學習。E-mail： Pchong1991@163.com

在現實世界中，數據量變得越來越大，越來越多的數據開始采用矩陣的形式存儲。由于存儲設備的損壞，網絡中信息傳輸不穩定導致傳輸過程中數據丟包等原因，出現了大量數據缺失的問題[1]，因此從非常有限的信息中估計缺失值這項技術變得尤為重要。矩陣補全技術被廣泛應用在很多領域。例如，圖像恢復[2]，視頻去噪[3]和推薦系統[4-5]等。在近二十年中，矩陣補全算法得到了長足的發展，其中基于低秩的模型具有顯著的性能[6-9]。基于低秩的模型通常對目標矩陣做出一個合理的假設，即目標矩陣是低秩的或近似低秩的，基于此假設，研究人員提出了矩陣補全問題的基礎建模[6]。然而，矩陣補全基礎模型秩最小化問題很難求解，為了解決這個問題，現有算法通常使用核范數來代替秩函數。理論研究表明核范數是最貼近秩函數的凸下界[10];采用核范數來近似代替秩函數的現有方法有很多，例如奇異值閾值（SVT）[11]，核規范正則最小二乘法（NNLS）[12]和魯棒性主成分分析（Robust PCA）[13]。研究發現，當矩陣存在較大奇異值時，核范數對矩陣秩的近似往往不夠精確，因此在實際應用中可能會獲得次優性能[14]。本文針對核范數對于秩函數的擬合不夠精確這一問題，提出了改進后的矩陣補全算法。相對于將矩陣所有奇異值直接相加的核范數，本文采用基于矩陣對數行列式的方式近似矩陣的秩，從而有效地減小較大的奇異值對矩陣低秩性質的影響。相比于核范數而言，對數行列式對于秩函數的近似更為精確。因此，本文通過采用對數行列式代替秩函數，得到了新的矩陣補全模型。

1 相關工作介紹

近些年，矩陣補全技術被廣泛應用于各種領域，包括機器學習，計算機視覺，信號處理等。最近的研究進展表明，基于核范數的矩陣補全算法對于低秩部分的近似不夠精確，針對這個問題本研究考慮采用對數行列式來解決。

1.1 對數行列式

對于任意矩陣X∈Rm×n，矩陣的對數行列式定義為

F（X）=logdet（I+XTX）（1）

顯然，logdet（I+XTX）=∑ni=1log（1+σ2i，X），其中，σ1，X>σ2，X>…>σn，X≥0，σi，X是矩陣X的第i個奇異值。

1.2 奇異值閾值算法（SVT）

SVT[11]算法是采用核范數近似代替秩函數從而實現矩陣補全的一種算法，模型為

minXX*+αX2Fs.t. PΩ（X）=PΩ（M）（2）

其中，X∈Rm×n是恢復出的矩陣;M∈Rm×n是給定的低秩的不完整的數據矩陣;α為平衡參數;Ω是一組對應于能被觀察到的項目的位置信息。PΩ（X）定義為：當（i，j）∈Ω時，PΩ（X）ij=Xij; 當（i，j）∈Ωc時，PΩ（X）ij=0。

通過使用對數行列式來對函數的低秩部分進行擬合，這種效果要好于核范數的擬合效果，本文采用這種方式成功的解決了核范數作為秩函數近似不夠精確的問題[14]。

2 本文方法

2.1 目標函數

考慮到核范數作為矩陣低秩部分的表現不夠理想，本文采用對數行列式作為對秩函數的非凸近似

min Xlogdet（I+XTX）s.t. PΩ（X）=PΩ（M）（3）

其中，I為單位陣;M∈Rm×n; X∈Rm×n是修復后的新矩陣。

2.2 模型的優化

由于難以直接優化目標函數，本文通過引入輔助變量來簡化模型，從而得到新模型

min logdet（I+XTX）s.t. W=X，PΩ（X）=PΩ（M）（4）

優化階段，本文采用了ALM（增廣拉格朗日法）[15]的優化算法，交替迭代優化每一個變量。給出模型的增廣拉格朗日方程式

L=F（X）+ρ2W-X+θρ2F（5）

其中，ρ 是平衡參數，θ 是拉格朗日乘子。

2.2.1 最小化X 關于X的子問題

Xt+1=argminX F（X）+ρt2Wt-X+θtρt2F（6）

其中，t為迭代次數。對于使用對數行列式的子問題，通過文獻[14]的證明，可知式（6）等價于求解

σ*i=argminσ*i∑ig（σ*i）+ρt2（σ*i-σi，H）2s.t. σ*i≥0，（i=1，…，n）（7）

其中，g（x）=log（1+x2）; σ*i是所求更新后的最優解X的第i個奇異值，H=Wt+θt/Pt，σi，H≥0，（i=1，…，n）是矩陣H的第i個奇異值。對關于σi的函數f（σi）=log（1+σ2i）+ρt2（σi-σi，H）2分別求一階導數和二階導數，得

f′（σi ） = 2σi 1 + σ2i+ ρt （σi -σi，H ）（8）

f''（σi ） = ρt σ4i+ （2ρt -2）σ2i+ （2 + ρt ）（1 + σ2i）2（9）

令f′（σi）=0，得

ρtσ3i-ρtσi，Hσ2i+（ρt+2）σi-ρtσi，H=0（10）

其中，σi≥0，（i=1，…，n）; 矩陣H的SVD是U diag（{σi，H}ni=1）VT; U，V均為單位正交矩陣，且UUT=I，VVT=I，U為左奇異矩陣，V為右奇異矩陣;diag（{σi，H}ni=1）是主對角線元素為σi，H，（i=1，…，n），其余元素為0的主對角矩陣;σi，H≥0，（i=1，…，n）。

本文通過兩種情況進行分析。

情況1：如果σi，H=0，由于σi≥0，可知f′（σi）≥0，故f（σi）是非減函數，因此，σi=0時，函數f（σi）最小。

情況2：如果σi，H>0，此時有f′（0）<0，f''（0）>0，因此至少存在一個根∈（0，σi，H）; 當ρt>0.25時，可以看出f''（σi）>0，因此f′（σi）是有唯一全局最優解的凸函數，此時σ*i可以通過f′（σi）=0求解得到。當0<ρt<0.25時，可以通過以下方式進行求解：刪掉式（10）求解中負根的集合，獲得解集Ο+，根據一階必要條件定理，可知σ*i=argminσi∈{0}∪Ο+f（σi）。

設置初始化ρt=0.000 1，且ρt隨著迭代次數不斷增大，在迭代到17次時，滿足ρt>0.25，通過這種方式，來保證當σi，H>0時，有σ*i∈（0，σi，H）; 當σi，H=0時，σ*i=0。

綜上，得到Xt+1的更新方式為

Xt+1=U diag（σ*1，…，σ*n）VT（11）

2.2.2 最小化W 關于W的子問題為

Wt+1=argminWρt2W-Xt+1+θtρt2F（12）

針對上述最小化問題，通過對式（10）中W求導，得到Wt+1的更新方式為

Wt+1=Xt+1-θtρt（13）

為了保證原圖像已知的像素值不變，加入約束條件PΩ（W）=PΩ（M），得到Wt+1的更新方式

Wt+1=PΩc（Wt+1）+PΩ（M）（14）

其中，Ωc是一組對應于矩陣中缺失項的位置信息。

2.2.3 其他變量的更新 關于變量ρ與θ的更新方式為

ρt+1=ρt×k（15）

θt+1=θt+ρt+1（Wt+1-Xt+1）（16）

其中，k>1，保證每次迭代ρ都是增大的。

上述優化算法可以歸為算法1。

算法1

輸入：需要處理的數據矩陣，以及缺失位置的下標;初始化ρ和θ。

（1） 給定最大的迭代次數matrix，迭代進行優化;

（2） 設置t=1，計算 max{Wt-Xt2F，Xt+1-Xt2F，Wt+1-Wt2F}≤0.001，判斷是否收斂;

（3） 根據式（11）計算Xt+1;

（4） 根據式（14）計算Wt+1;

（5） 根據式（15）計算ρt+1，根據式（16）計算θt+1;

（6） 跳轉至第二步直到收斂;

（7） Return Xt+1。

3 實驗及結果分析

實驗采用和SVT[11]算法相同的參數初始值，令ρ=0.000 1。當迭代進行到17次時，ρ>0.25，此時滿足實驗方法所需條件，可以認為本文算法在前16次的迭代中，提供了滿足實驗條件的初始化。

3.1 對比方法及實驗數據

為保證實驗的有效性，選取實驗數據時，借鑒文獻[16]，選用對比度較為明顯的圖1～圖4，能夠更直觀的看到對比實驗效果。實驗設計時，分別進行了25%，50%，75%的隨機缺失值處理，并記錄缺失值的位置。在對比實驗部分，選用經典的SVT（奇異值閾值算法）。

3.2 恢復圖像對比

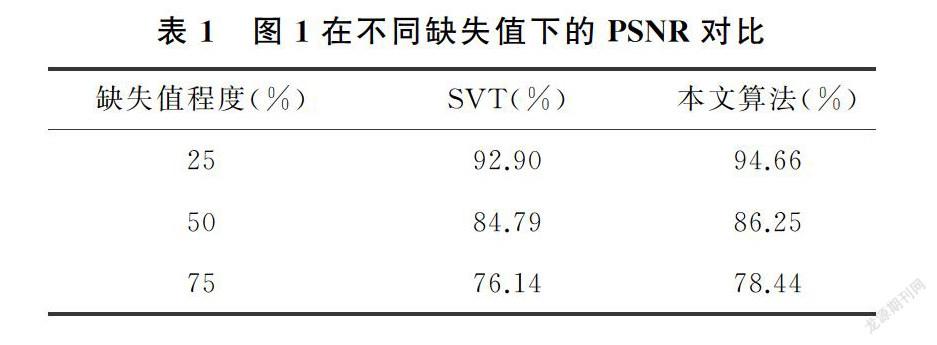
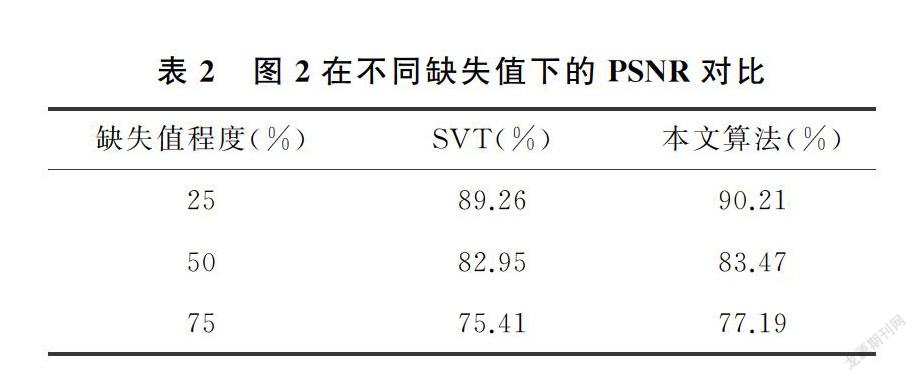
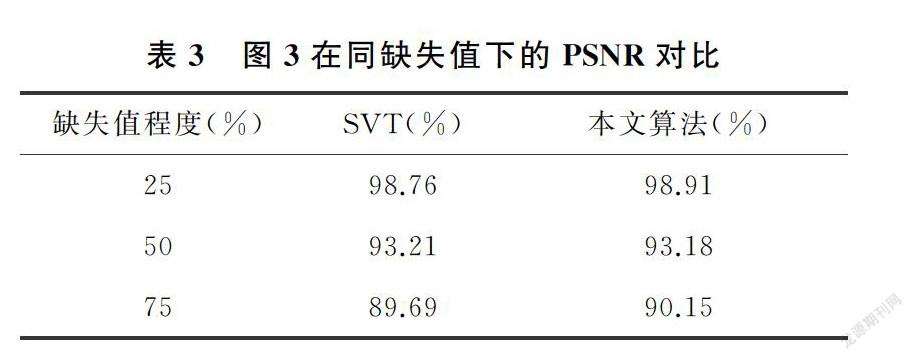
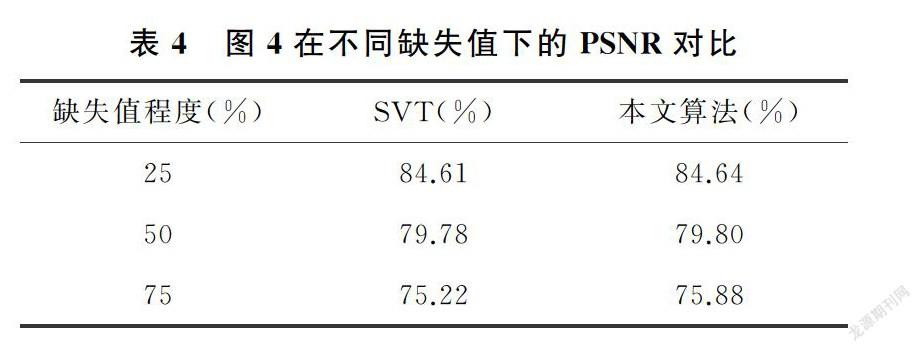
圖1～圖4，展示了矩陣補全算法的對比實驗效果圖（原數據圖片節選自文獻[16]，下載鏈接為https：//github.com/xueshengke/TNNR）。實驗選用隨機添加了75%缺失值的噪聲圖像的矩陣補全效果圖作為展示。從圖1～圖4的對比圖展示部分，不難看出，新算法恢復后的圖像噪聲信息更少，色彩飽和度和局部圖像質量更加接近原圖像。

3.3 PSNR值比較

實驗中選用PSNR值來衡量恢復后的圖像質量，PSNR值越大，表示恢復出的圖像質量越好。對三種不同噪聲水平的圖片，分別用SVT算法和本文的算法分別進行圖像恢復，并記錄修復后圖像的PSNR值，記錄在表1～表4中。

從表1～表4展示的實驗結果很容易發現，在相同條件下，修復后的圖像在PSNR值的對比上，使用本文方法獲得的PSNR值較大，矩陣補全效果明顯好于經典的SVT算法。實驗驗證了本文的猜想，相比于SVT算法采用核范數近似秩函數的做法，采用對數行列式的方式，能夠更好的作為秩函數的近似，充分利用了數據矩陣的低秩性質，提高了矩陣恢復的效果。

3.4 收斂性分析

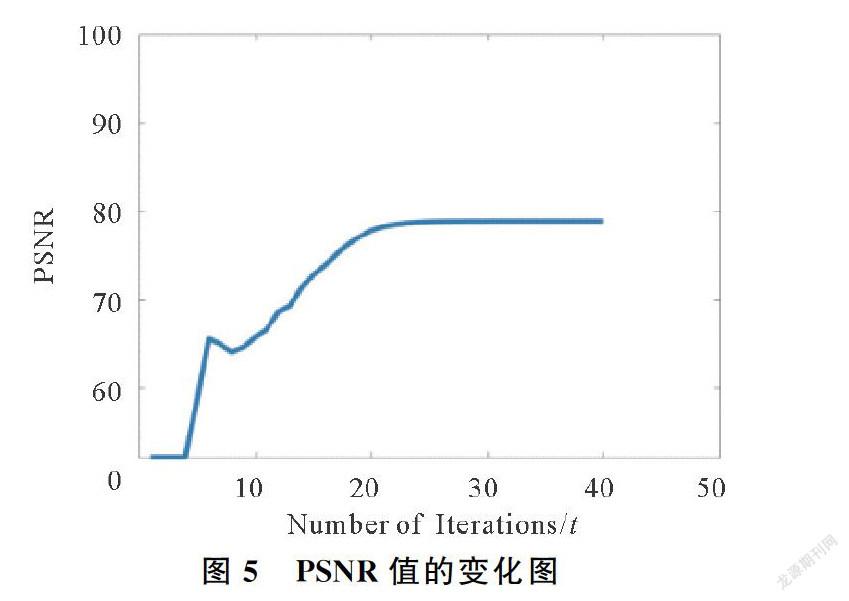
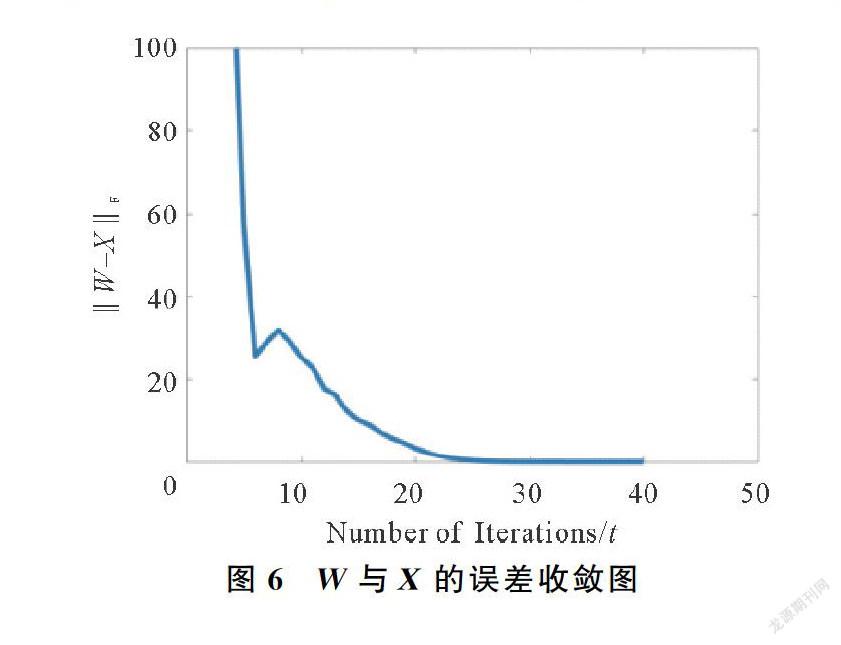
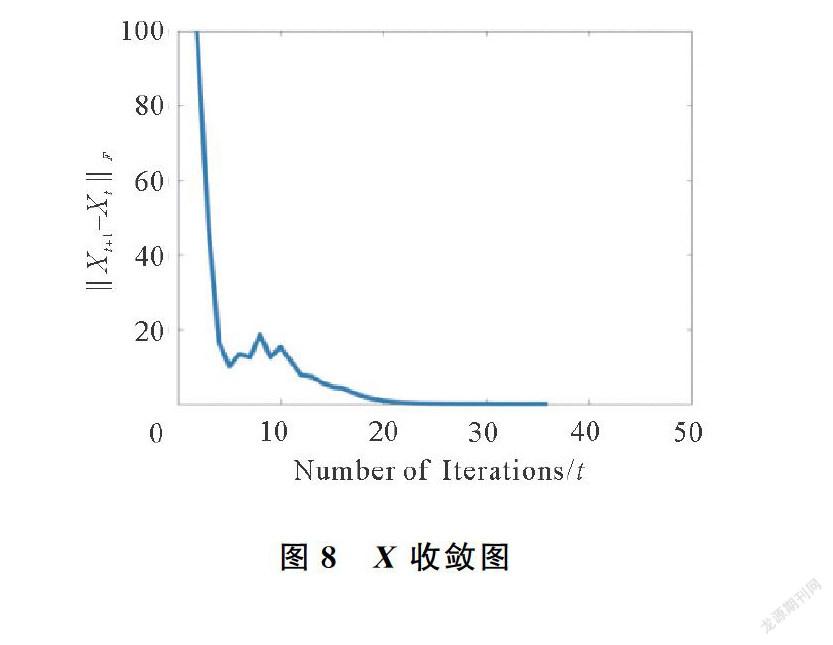
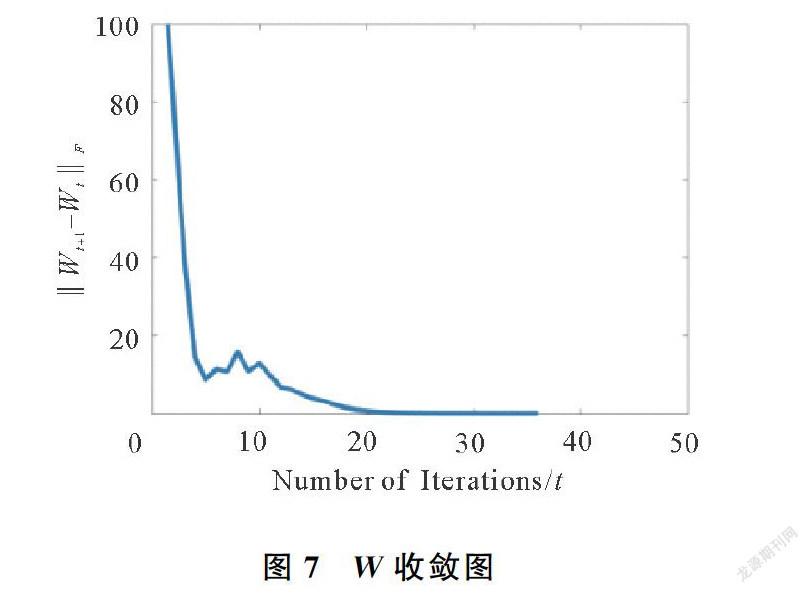
為了測試本文方法的收斂性，實驗設計中本文針對圖1分別計算了每次迭代中的PSNR值，W-X2F，Xt+1-Xt2F，以及Wt+1-Wt2F的值，收斂圖分別如圖5～圖8所示。可知，在迭代40次左右，模型已經收斂。

4 結論

本文提出了一種新的矩陣補全算法的模型。在目標函數低秩性部分改進了核范數替代秩函數不夠精確的問題，采用對數行列式代替核范數作為秩函數的近似。在實驗優化部分，本文采用ALM的優化方式對模型進行優化，解決了非凸問題優化困難的技術難點。在所設計的圖像補全實驗中，本文算法表現良好，證明了其有效性。

參考文獻

[1]王興宏.大數據應用及新時期所面臨的挑戰研究[J].青島大學學報（自然科學版），2020，33（3）：22-27.

[2]NIKOS K. Image completion using global optimization[C]//Computer Vision and Pattern Recognition. New York， 2006： 442-452.

[3]JI H， LIU C， SHEN Z， et al. Robust video denoising using low rank matrix completion[C]// 23rd IEEE Conference on Computer Vision and Pattern Recognition， CVPR. San Francisco， 2010： 13-18.

[4]STECK H. Training and testing of recommender systems on data missing not at random[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington， 2010，713-722.

[5]KANG Z， PENG C， CHENG Q. Top-N recommender system via matrix completion[C]// 30th Association for the Advancement of Artificial Intelligence （AAAI） Conference on Artificial Intelligence. Phoenix， 2016，179-184.

[6]CANDES E J， RECHT B. Exact matrix completion via convex optimization[J]. Computational Math， 2009， 9： 717-772.

[7]CANDES E J， TAO T. The power of convex relaxation： Near-optimal matrix completion[J]. IEEE Transactions on Information Theory， 2010， 56（5）：2053-2080.

[8]LIU J， MUSIALSKI P， WONKA P， et al. Tensor completion for estimating missing values in visual data[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2013， 35（1）：208-220.

[9]ERIKSSON A， HENGEL A V D. Efficient computation of robust low-rank matrix approximations in the presence of missing data using the L1 Norm[C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco， 2010： 771-778.

[10] RECHT B， FAZEL M， PARRILO P A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization[J]. Siam Review， 2010， 52（3）：471-501.

[11] CAI J， CAND E J， SHEN Z. A singular value thresholding algorithm for matrix completion[J]. Siam Journal on Optimization， 2008， 20（4）：1956-1982.

[12] TOH K C， YUN S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems[J]. Pacific Journal of Optimization， 2010， 6（3）：615-640.

[13] PENG C， CHEN Y， KANG Z， et al. Robust principal component analysis： A factorization-based approach with linear complexity[J]. Information Sciences， 2019， 513： 581-599.

[14] PENG C， KANG Z， LI H， et al. Subspace clustering using log-determinant rank approximation[C]//Proceedings of the 21th ACM SIGKDD international conference on Knowledge Discovery and Data Ming.Sydney，2015：925-934.

[15] YANG J， YUAN X. Linearized augmented lagrangian and alternating direction methods for nuclear norm minimization[J]. Mathematics of Computation， 2012， 82（281）：301-329.

[16] HU Y， ZHANG D B， YE J P， et al. Fast and accurate matrix completion via truncated nuclear norm regularization[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence， 2013， 35（9）：2117-2130.

Matrix Completion Algorithm Based On Log-determinant

QIN Guo-feng， PENG Chong， WEI Ji-peng

（College of Computer Science and Technology， Qingdao University， Qingdao 266071， China）

Abstract：

The nuclear norm constraint is mainly used for the target matrix in traditional matrix completion models based on low-rank assumptions. However， the nuclear norm is not accurate enough to approximate the rank function. Thus it may lead to degraded performance in low-rank recovery problem. To resolve the drawback of the nuclear norm in low-rank recovery， the log-determinant is used to replace nuclear norm and the matrix completion model based on the log-determinant minimization is proposed. Experimental results show that proposed method can effectively recover the low-rank structure of the target matrix and complete the missing entries of corrupted images in image completion application.

Keywords：

matrix completion; low-rank structure; log-determinant; machine learning