射流角度對氣動矢量噴管的影響及優化
陳航

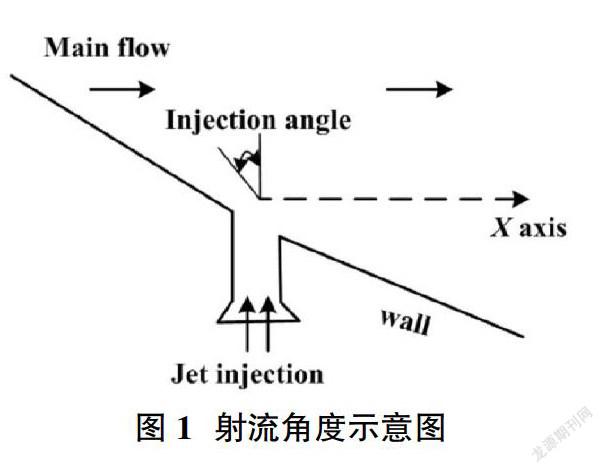
摘要:采用數值模擬方法計算分析了射流角度對氣動矢量噴管流動結構和性能的影響。基于試驗設計和近似模型方法,結合數值模擬,構建了氣動矢量噴管模型。將氣動矢量噴管模型集成到發動機總體性能程序中,以某航空發動機為研究對象,分析了發動機不同狀態下的氣動矢量噴管性能情況。研究結果表明:在一定的幾何與氣動參數條件下,存在使氣動矢量角最大的射流角度。隨著發動機進口溫度和引氣量的增加,氣動矢量角最大模式下的射流角度均逐漸減小,垂直噴射或順流向對提升噴管推力系數有利。
關鍵詞:氣動矢量噴管;試驗設計;近似模型;射流角度;氣動矢量角
中圖分類號:V233.757? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼:A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號:1674-957X(2021)11-0004-02
0? 引言
氣動矢量噴管在減輕發動機重量、減少成本、實現飛機后體與發動機高度一體化方面具有明顯的技術優勢,是未來高推重比渦扇發動機的首選技術方案之一[1]。相對于機械式矢量噴管,氣動矢量噴管內部流動復雜,涉及到二次流噴射對超聲速主流的摻混、流動分離和激波,且影響因素更多,并呈現高度的非線性和多因素交互性。對于氣動矢量噴管,國內外學者基于數值模擬和試驗技術開展了大量的研究工作[2-5],對其性能和響應規律進行不斷的探索,得到了主、次流氣動、幾何參數對噴管推力矢量的定量影響關系。
但目前的研究大都集中在氣動矢量噴管本身,沒有考慮發動機和氣動矢量噴管的耦合,且不涉及二次流射流角度的控制研究。本文從氣動矢量噴管模型入手,開展不同射流角度對噴管流動情況的數值模擬計算分析。基于試驗設計和近似模型構建了氣動矢量噴管模型,建立了主、次流氣動、幾何參數和噴管性能參數之間的關聯關系。將氣動矢量噴管模型集成到航空發動機總體性能程序中,使噴管主次流進口參數與發動機模型相關聯,對發動機不同狀態下的噴管推力矢量特性進行分析,對二次流射流角度變化規律進行研究。
1?; 數值方法
1.1 物理模型與網格劃分
本文研究的氣動矢量噴管是結構參數如表1所示的二元矩形收-擴噴管,并通過自編程序控制射流口位置和角度(下壁面為單排射流口)。射流角度的規定見圖1,以主流方向為基準(0°),逆主流方向為射流角大于90°方向。
1.2 邊界條件和求解方法
主流和二次流進口選用壓力進口邊界,給定總溫、總壓,出口選用壓力出口,給定靜壓,噴管外流入口給定黎曼邊界條件,壁面條件設定為絕熱、無滑移條件。
采用變步長四階Runge-Kutta方法進行時間推進求解,對流項采用二階迎風格式離散求解,粘性項采用中心差分格式。湍流模型選擇SST k-ω湍流模型,同時由于擴張段噴管氣流達到了超聲速,因此選用基于密度的穩態方程,流體介質選用理想氣體。
2? 射流角度對氣動矢量噴管性能影響
射流角θ會對次流與主流摻混時的動量及能量交換產生較大影響,從而影響到摻混流場結構,并最終影響噴管矢量性能。選取二次流相對位置0.7,NPR=8、10、12,SPR=0.8、1.0、1.2時,對θ取90~130°時的噴管矢量性能作了研究。
隨著射流角度θ的增大,氣動矢量角增大,可見射流角度θ對噴管流場結構有較大影響。但當射流角度θ增大到一定程度時,在射流角度θ=110°、120°時氣動矢量角基本相同,噴管內部流場結構變化不再明顯,繼續增大射流角度,氣動矢量角反而降低,即在一定的幾何與氣動參數條件下,存在一個最佳的噴射角度,使得噴管氣動矢量角達到最大。
3? 氣動矢量噴管模型研究
3.1 氣動矢量噴管試驗設計方法
影響氣動矢量噴管的因素很多,DOE試驗設計方法以其獨有的多維數組均值算法可以有效地應對多變量、大范圍的影響參數,合理安排試驗參數的組合,使得試驗點大大減少,且具有較好的可信度。本文中選用的最優拉丁采樣算法,該方法保證每個因子選取的不可重復性,并可以使所有的試驗點盡量均勻地分布在設計空間,具有非常好的空間填充性和均衡性。
為研究二次流射流口位置和角度對氣動矢量噴管性能的影響,通過自編程序用來控制二次流射流口位置和角度,搭建了基于DOE試驗設計方法的氣動矢量噴管特性計算流程。
影響氣動矢量噴管性能的因素主要有:
主流落壓比(NPR):4.5~18;二次流總壓比(SPR):0.8~1.2;二次流射流口相對位置(x/x1,相對于擴張段軸向長度):0.5~0.8;射流角度(θ,相對于主流方向):90~140°。
對以上因素對噴管性能的影響進行計算和分析。
對以上4個因素分別取值86個試驗點,生成設計矩陣,并進行計算。
3.2 氣動矢量噴管近似模型構建
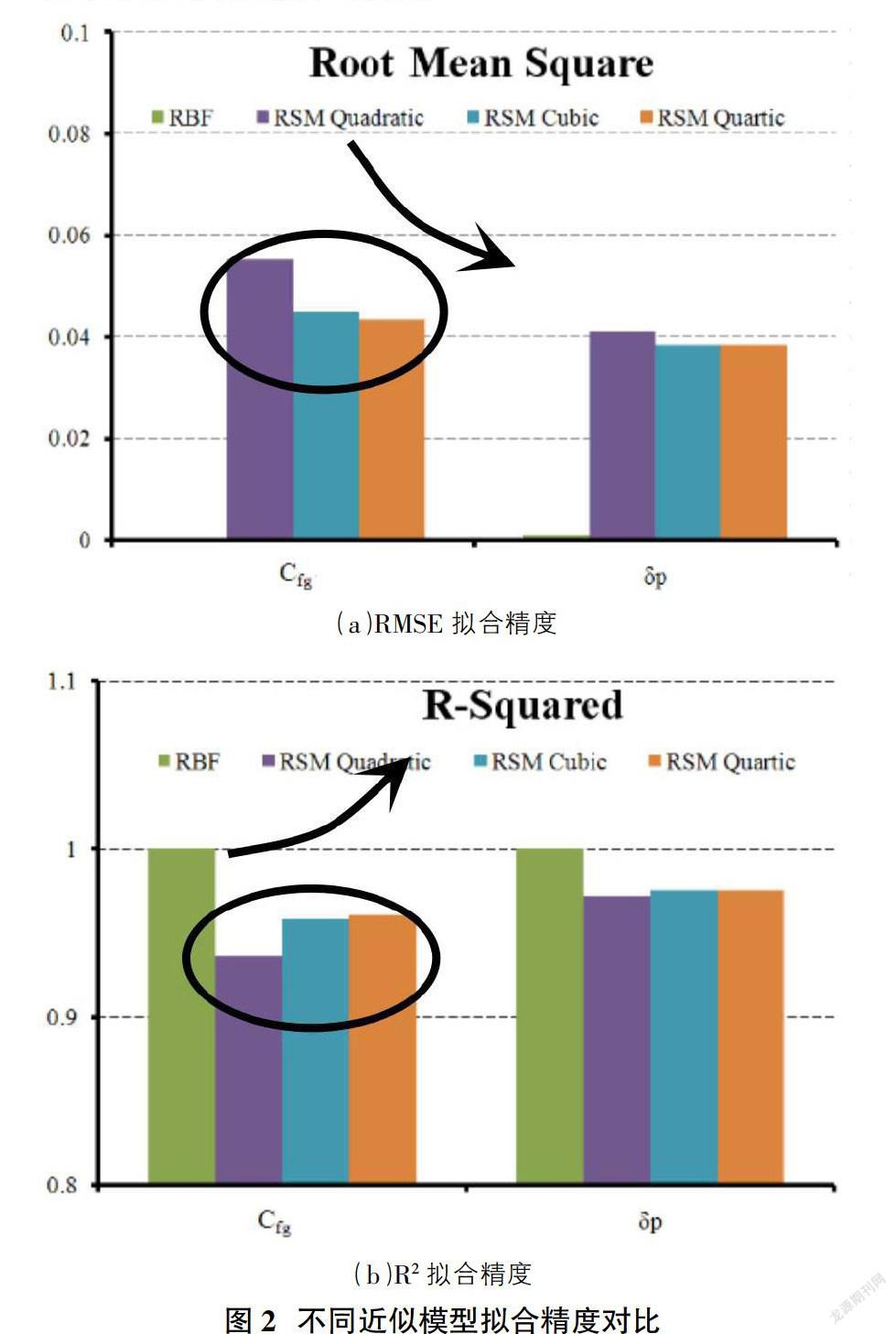
為對比不同近似模型的精度,本文分別采用徑向基RBF神經網絡模型及多項式回歸模型對上述得到的氣動矢量噴管數值模擬結果進行近似建模,同時做了二階、三階和四階的對比分析,對擬合精度和可信度進行比較分析。
對樣本數據擬合度可用均方根誤差(RMSE)相對值和決定系數R2兩個標準檢驗,RMSE→0表示響應值誤差小,R2→1則表明響應值與原模型相似度高。
徑向基神經網絡模型以其強大的逼近復雜非線性函數的能力偏差最小,擬合精度最高。也說明氣動矢量噴管具有高度的非線性及相互的關聯性,利用多項式回歸方法很難完整的表達出其特性。
4? 氣動矢量噴管二次流射流角度的優化
對于氣動矢量噴管,二次流射流位置是固定的,可調節幾何參數的只有射流角度,開展氣動矢量噴管射流角度控制規律的優化,可以為氣動矢量噴管的設計和控制提供參考。
將構建的氣動矢量噴管模型集成到發動機總體性能程序中,構建二次流引氣流路及噴管主流進口參數接口,以某高推重比發動機為研究對象,進行氣動矢量噴管二次流射流角度規律的研究。
計算條件:二次流射流口相對位置x/x1=0.7;優化變量:二次流入射角度θ;變量范圍:90~140°;引氣位置:外涵道進口。
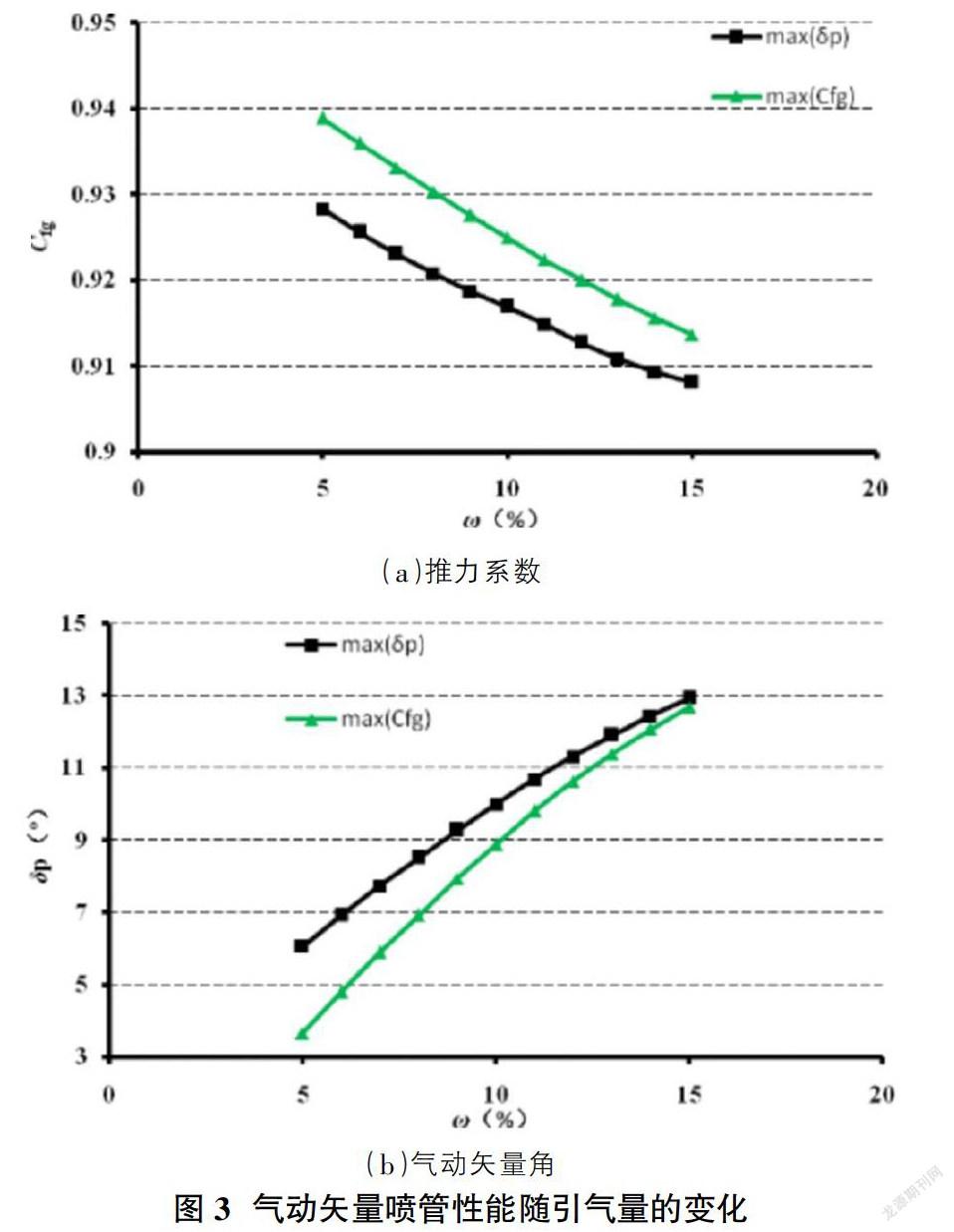
二次流引氣量為外涵進口截面的5~15%,開展不同引氣量對氣動矢量噴管性能影響的計算分析。隨著引氣量的增加,使得噴管內產生的斜激波強度增強,氣動矢量角增加,推力系數減少,氣動矢量角最大優化模式的二次流射流角度逐漸減小,在引氣量為外涵進口截面的5%增大到15%時,矢量角最大模式下的二次流射流角度從130°減小到103°,推力系數最大模式下二次流射流角度依然保持優化范圍最小角度90°。
在引氣位置固定之后,二次流射流角度是氣動矢量噴管的重要影響因素,因此,在氣動矢量噴管的設計過程中,需要對發動機不同工作狀態下的氣動矢量角和推力系數進行綜合考慮,提升發動機性能。
5? 結論
①在一定的幾何與氣動參數條件下,存在一個最佳的噴射角度,使得噴管氣動矢量角最大。②氣動矢量噴管具有高度的非線性及多影響因素的交互性,通過與多項式回歸模型的對比,徑向基神經網絡模型更適合用于表達氣動矢量噴管特性。③隨著發動機進口溫度和引氣量的增加,氣動矢量角最大對應的二次流射流角度均逐漸減小,垂直主流噴射或順流向對提升噴管推力系數有利,氣動矢量噴管的設計要在氣動矢量角和推力系數中進行綜合選取。
參考文獻:
[1]Deere K A Computational Investigation of the Aerodynamic effects on Fluidic Thrust Vectoring. AIAA2000-3598,2000.
[2]Deere K A. Summary of fluidic thrust vectoring research conducted at NASA Langley Research Center[R]. AIAA 2003-3800.
[3]賈東兵,周吉利,鄧洪偉.固定幾何氣動矢量噴管技術綜述[J].航空發動機,2012(6):29-33,42.
[4]王占學,李志杰.噴管主次流氣動參數對流體推力矢量影響的數值模擬[J].推進技術,2008,29(2).
[5]王占學,王玉男,李志杰,辛曉龍.基于激波控制的流體推力矢量噴管試驗[J].推進技術,2010,31(6):751-756.

