深埋隧道拱部圍巖潛在塌落破壞上限有限元分析

胡昌文，韋彬，戴智穎，楊峰，趙煉恒

(1. 深圳市綜合交通設計研究院有限公司，廣東 深圳518003；2. 中南大學 土木工程學院，湖南 長沙410075)

隧道開挖后圍巖受到擾動而應力重新分布[1]，形成局部落石[2]、剪切破壞[3]等危害隧道施工安全的破壞形式，且多以拱部巖體塌落形式發生[4?5]。隧道拱部塌落和圍巖壓力研究常用理論分析、數值模擬和現場監測等方法。如普羅托奇雅闊諾夫推出平衡拱理論；太沙基建立松散介質理論以確定襯砌垂直壓力公式和滑動面[6]。目前，巖土極限分析成為解決隧道圍巖穩定性與破壞模式問題的有力手段。如王永甫等[7]建立了圓形隧洞塌落破壞模式滑移線方程。武軍等[8]以顆粒流橢球體理論改進太沙基松動壓力公式。SAHOO 等[9]采用上限有限元分析多參數條件下圓形隧道圍巖壓力。LI等[10]運用Hoek-Brown 破壞準則及上限定理，明確了多圓弧截面深埋隧道坍塌機理。FRALDI 等[11]用變分法極限分析建立了矩形隧道塌落力學模型。HUANG 等[12]獲得了孔隙水壓力下隧道塌落數值解。劉俊等[13]采用強度折減法分析了淺埋隧道塌落破壞。白維仕等[14]以滑移線方式評價了黃土隧道坍塌拱及承載性能。孫雁軍等[15]運用運動單元上限有限元揭示了隧道工作面滑移線網塌落形態。耿永旺[16]采用離散元分析了黃土隧道塌落拱形態特征。現有文獻多傾向于研究淺埋隧道，如YANG等[17]對不同跨度影響下的淺埋隧道破壞進行了系列分析。通常隧道跨度增加時，圍巖擾動范圍更廣，當隧道埋深較大時，拱部易形成潛在的塌落和松動范圍，這種現象對于深埋土質隧道更為顯著。本文應用運動單元上限有限元法，研究極限狀態下不同跨度深埋隧道拱部的潛在塌落與松動范圍，分析隧道穩定性系數和破壞規律，為施工技術方案和風險防范措施制定提供一定的參考和借鑒。

1 問題描述與假設條件

圖1為本文建立的隧道拱部潛在塌落破壞分析模型圖。假設模型滿足如下條件：

1) 隧道圍巖為均質各向同性材料，破壞服從摩爾-庫倫屈服準則，容重為γ，內摩擦角為?，剪脹角為?，黏聚力為c；

2) 隧道處于未支護毛洞狀態，且只考慮高度為h，寬度為B(半寬為b)的上臺階，隧道輪廓簡化為橢圓形；

3) 隧道埋深足夠大，荷載僅考慮圍巖自重，模型依對稱性取右側一半。

如圖1 所示，以b/h表示無量綱跨度參數，其中h不 變，b/h依 次 取1.00，1.25，1.50，1.75，2.00。圍巖內摩擦角?取35°～50°(按1°遞增)。以?/?表示剪脹角的影響，取0.0，0.2，0.4，0.6，0.8，1.0共6組值。

圖1 隧道拱頂潛在塌落破壞分析模型Fig.1 Analysis model diagram of potential collapse failure of tunnel vault

圖1中l2為隧道埋深，設置l2/h大于20。l1表示模型水平方向范圍，可取l1=l2。模型左側邊界Q1Q2水平速度為0(u=0)，下部邊界Q3Q4和右側邊界Q4Q5水平、豎向速度均為0(u=0，v=0)，隧道輪廓Q2Q3為自由邊界。

考慮隧道拱部潛在塌落破壞由圍巖自重引起，故選用無量綱量容重系數γh/c作為評價指標。于是，極限狀態下對應于臨界容重γcr，容重系數γcrh/c與隧道跨高比b/h，內摩擦角?和剪脹參數?/?關聯，即：

2 上限有限元模型建立

上限有限元模型劃分為剛性單元，單元間設置速度間斷線[18]。每個單元具有水平和豎向2 個自由度，極限狀態下僅速度間斷線上發生能量耗散。每個節點位置為變量，計算過程可實現間斷線的優化調整，進一步通過多次網格更新形成由有效間斷線網組成的近似滑移線網破壞模式。

對于隧道拱部潛在塌落破壞分析，可將圍巖臨界容重γcr作為目標函數，由上限定理其非線性規劃目標函數表達式為：

式中：Pd,i為第i條間斷線上的耗散能，nd為速度間斷線的總數。

非線性規劃的約束條件如式3(a)～3(h)所示：

式(3(a))為速度間斷線非線性約束，而ξ′i，ξ″i為間斷線上的過程變量。式(3(b))～(3(f))分別為Q1Q5和Q2Q3上的幾何邊界條件，式中ng1～ng5對應于各個邊界上的節點數目。式(3(g))約束單元面積為正值，其中ne為單元總數；式(3(h))表示求解臨界容重γcr時需施加的體力約束。Q1Q2，Q3Q4和Q4Q5上的速度邊界條件見上節。

應用能量等效屈服面將最初的土體強度參數?和c按剪脹角?的不同轉化為等效參數?*和c*[19]，如式(4)和式(5)所示：

3 臨界容重系數γcrh/c計算結果

3.1 計算結果對比

當隧道斷面為圓形時，臨界容重γcr已有相關研究，對應于本文b/h=1的情況，以下均以γcrh/c進行對比分析。取?=30°，?=30°，對應的數據如表1。

表1 臨界容重系數γcrh/c計算結果對比Table 1 Comparison of calculation results of critical bulkdensity coefficient γcrh/c

可看出，本文γcrh/c上限解處于SAHOO 和ZHANG Jian 計算結果之間，與SAHOO, ZHANG Jian ,YANG Feng 和BANERGEE 的計算結果差距分別為26.0%，4.6%，6.0%和22.0%。比較而言，本文數值偏大，這源于隧道按上臺階半斷面的情況考慮，即半圓形狀對應的潛在塌落破壞，故得出γcrh/c計算數值稍大，論證運動單元上限有限元解答可靠。

3.2 臨界容重系數γcrh/c規律分析

利用運動單元上限有限元對隧道塌落破壞時的臨界地層容重進行分析，按上述不同b/h，?和?/?對應獲得臨界容重系數γcrh/c關系曲線見圖2。

圖2(a)為?/?=0 時，γcrh/c上限解與內摩擦角?以及b/h的關系曲線。由圖可知，γcrh/c上限解隨內摩擦角?的變化較小，呈現出先增長后緩慢下降的趨勢，而γcrh/c上限解隨隧道跨度的增加而減小。

圖2(f)為ψ/?= 1時，γcrh/c上限解與內摩擦角?以及b/h的關系曲線。分析可知，隧道跨度增大將顯著降低破壞時的臨界容重γcr，如內摩擦角45°時，b/h=2 對應的臨界容重系數γcrh/c僅為b/h=1 時的39.5%，說明隧道跨度增加地層穩定性顯著下降。此外，不同于圖2(a)ψ/?= 0 情況，ψ/?= 1 時隨內摩擦角?增長，γcrh/c增長近似于線性增長關系。當隧道跨度大時，γcrh/c隨內摩擦角?增長的斜率變小。

通常，ψ/?介于0～1 之間，其值越接近于1 則剪脹效應越顯著。對比圖2(a)～2(f)可看出，γcrh/c上限解隨剪脹參數ψ/?增大而增大；在這個過程中，γcrh/c上限解曲線逐漸上揚，其數值與內摩擦角的關聯度變大；反之，剪脹參數ψ/?較小時，γcrh/c與?關系曲線轉變為一略微上凸的拋物線。

圖2 臨界容重系數γcrh/c與影響因素關系Fig.2 Relationship between critical bulk density coefficient γcrh/c and influencing factors

4 圍巖潛在塌落破壞模式

4.1 圍巖潛在塌落破壞模式對比

運動單元上限有限元程序可得到隧道拱部圍巖潛在塌落破壞模式。選取?=35°，ψ/?= 0 和1 對應的破壞模式繪制如圖3。

圖3展示了速度值分布云圖，該值經過歸一化處理，取值范圍處于0～1 之間。圖3 中還疊加有效速度間斷線組成的滑移線網，并以虛線表示按太沙基圍巖壓力理論繪制的破壞面。

圖3 圍巖潛在塌落破壞模式的相對速度矢量值云圖(?=35°)Fig.3 Relative velocity vector nephogram of potential collapse failure of surrounding rock in tunnel arch(?=35°)

由滑移線網看出，本文得到的破壞模式與太沙基理論的破壞面大致吻合。但本文破壞范圍限制于一定高度范圍內，這符合深埋隧道潛在塌落破壞限于局部的共識。由速度云圖可知，可見耗散能占比前80%的塊體單元集中于隧道拱部較小區域，該處可認為圍巖潛在塌落范圍，這與含平衡拱在內諸多理論相符[12,22?23]。在滑移線范圍內還存在速度很小塊體，此時間斷線上耗散能很小，用上限原理僅能論證處于極限狀態，與發生潛在塌落破壞還存在一些差異。

4.2 圍巖潛在塌落破壞模式的參數影響分析

為揭示不同參數取值條件下隧道拱部圍巖潛在塌落破壞幾何形態的演變規律，繪制系列滑移線網破壞模式如圖4所示。

1) 內摩擦角?的影響

圖4(a)～4(d)為圓形隧道ψ/?= 0 和1，?=35～50°時計算得到滑移線網破壞模式。可看出，當?減小時，臨界容重系數γcrh/c隨之減小，隧道上方破壞范圍快速增加。例如，ψ/?= 1 時，當內摩擦角?從40°降低到35°時，潛在塌落高度增長了59%，臨界容重系數減少了19%。通常，內摩擦角降低圍巖更易發生剪切破壞，引起更大范圍塌落和松動趨勢。

圖4(e)展示了?=35°～50°時，隧道拱部破壞范圍外輪廓圖，可看出塌落范圍增長關聯了內摩擦角減小，破壞模式頂端滑動面的傾角等于圍巖內摩擦角。

2) 隧道跨度和高度比b/h的影響

圖4(f)～4(i)列出了ψ/?= 0 和1，?=45°，b/h=1.25～2.0 對應滑移線網破壞模式。由圖可知，當b/h增大，即隧道跨度增大時，上方潛在塌落土體范圍不僅在橫向上增長，在豎向范圍也有較大增長，這也是臨界容重系數隨隧道跨度增長而快速下降的原因。

圖4(j)展示了b/h=1.0～2.0 對應的隧道拱部破壞范圍外輪廓圖。對比圖4(e)可知，潛在塌落破壞范圍受內摩擦角和隧道跨度兩方面的影響，內摩擦角的改變引起塌落體形狀，而不同跨度隧道對應的潛在塌落范圍雖有改變，但外側輪廓差異并不大。

3) 剪脹參數?/?的影響

圖4(g)和圖4(k)～4(n)為?=45°，b/h=1.5，ψ/?=0～1時的滑移線網破壞模式，可以看出隨著剪脹參數增大，剪脹效應使得外側圍巖受到剪脹變形土體所產生的壓力，使圍巖塌落破壞范圍減小，上限解增大。如ψ/?從0 增至1 時，塌落范圍減小56%，上限解增長83%。

圖4(o)展示了?=45°，b/h=1.5 時不同ψ/?對應的外輪廓，可知塌落范圍隨ψ/?增大而減小趨勢，隨ψ/?增大而放緩，如ψ/?從0 到0.2，塌落面積下降32.1%，而ψ/?從0.8 到1，塌 落 面 積 僅 下 降2.9%。

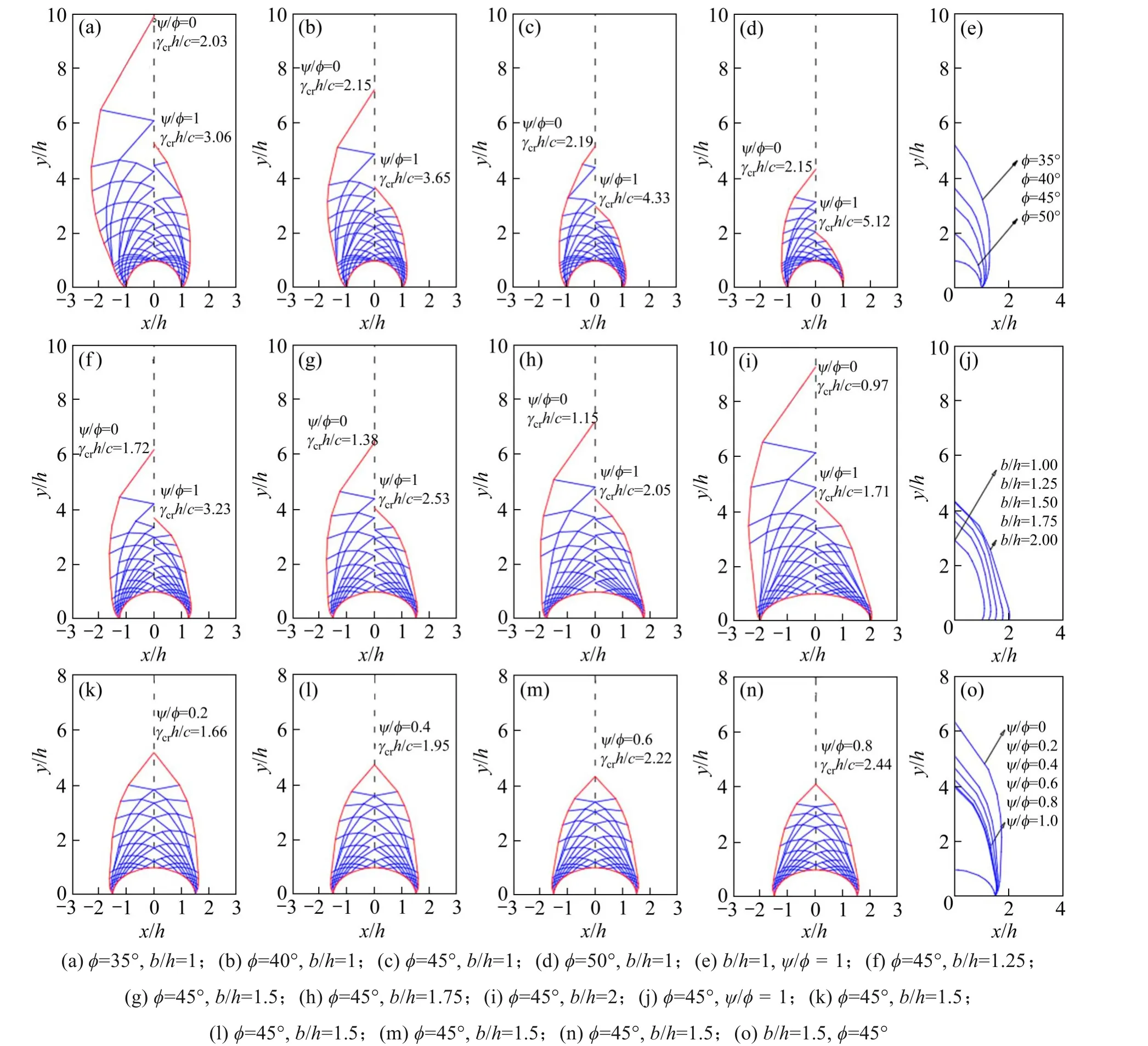
圖4 隧道拱部圍巖潛在破壞模式演變規律Fig.4 Evolution law of potential failure mode of surrounding rock at tunnel arch

5 結論

1)當ψ/?= 1 時，臨界容重系數γcrh/c隨?的增長而線性增長，隨b/h的增長而快速降低；當ψ/?=0 時，γcrh/c隨?增長的變化不顯著，而與b/h呈反比例關系。

2)內摩擦角?增長時，隧道拱頂圍巖潛在塌落范圍增長迅速，且塌落形狀有所變化；b/h增長時塌落范圍增長放緩，且塌落拱外輪廓保持不變。

3)當?增長時，圍巖破壞范圍離拱頂稍遠區域相對速度變得很小，b/h增長使得拱頂上方速度集中區域范圍增長，同時γcrh/c迅速減小。